抓核心素养·应用经验·品智慧课堂
2018-01-11江苏省南京市溧水区晶桥中心小学魏玉琴
江苏省南京市溧水区晶桥中心小学 魏玉琴
“数学素养”是人在先天基础上,受后天环境、数学教育等影响,所获得的数学知识技能、数学思想方法、数学能力、数学观念和数学思维品质等融于身心的一种比较稳定的心理状态。
《义务教育数学课程标准(2011年版)》明确提出: 在数学课程中,应当注重发展学生的数感、符号意识、空间观念、几何直观、数据分析观念、运算能力、推理能力和模型思想。形成思维模式,会证明、归纳、抽象、比较、迁移,具有深度思维的能力。
一、抓住细节,精心培养
小学生在学习解决问题的策略时,无论成绩优异与否,都容易理不清题意,产生做题失误。
1.比较式读题
李师傅每小时加工24个零件,8小时加工多少个?
李师傅每小时加工24个零件,加工192个零件要用多少小时?
李师傅8小时加工了192个零件,平均每小时加工多少个零件?
这3个例子看起来相似,实则同属于一个数量关系:工作效率×工作时间=工作总量。只要紧紧抓住这一数量关系,就可着重培养学生的读题能力,一定要思考万变不离其宗的数量关系,找出第一题的数量关系,下面两题便迎刃而解,甚至可以利用第一题的答案来验证下面两题的正确性。
2.综合法式读题
综合法是指从已知条件出发,借助其性质和有关定理,经过逐步的逻辑推理,最后达到待证结论或所求问题,其特点和思路是“由因导果”,即从“已知”看“可知”,逐步推向“未知”。
①小营村原来有一个宽20米的长方形鱼池。因扩建公路,②鱼池的宽减少了5米,③这样鱼池的面积就减少了150平方米。现在鱼池的面积是多少平方米?
在读题的时候,一定要学生去思考:这道题讲的内容是什么?有哪些条件?根据有用的两个条件可以推出什么?然后引导学生确立解题的思路,找出解题的方法。从条件①和②,推出现在的鱼池宽是15米,长不变。根据条件③就可以推出长是多少,最后求出鱼池的面积。
解决问题的策略,综合法比分析法会让学生更加容易理解题目,从条件想问题,逐步推理。经过长期的训练,学生能下意识地反应出两条件组合能擦出什么火花。一开始这样做的时候,学生会很不适应,教师可以放慢节奏、稳步前进,经过长时间的课堂训练,学生就养成了精心读题、读完思考的好习惯。这样的好习惯一旦养成,受益终身。
二、抓住经验,引起共鸣
小学数学中的应用题往往取材于生活,不仅要多去体验生活,更重要的是,要把生活中经历的问题与数学联系起来,同时,数学问题也要与生活经历紧密相连,做到“数学起源于生活”。
案例——“认识人民币”。
课堂伊始,教师播放一则动画,动画内容是森林里举办了一场动物大赛,大家都很拼命地参加了比赛,于是大象爷爷想要对大家进行奖励,所有的动物们都乐开了花。大象爷爷想要征求大家的意见,小猴率先跳起来说:“发桃子,发桃子。”小兔也争先恐后地说:“发萝卜,发萝卜。”小猫更加气愤:“发鱼,发鱼。”松鼠说一定要发坚果……这下让大象爷爷犯了难,所有的人都不一样。同学们,你们说应该发什么奖品来平息这场斗争而以示公平呢?于是一个小朋友站了起来说:“发钱最公平!”
这是一年级中的认识人民币的内容,若平铺直叙,直截了当地教授人民币,略显枯燥和生硬,而此处创设情境,将生活中的人民币和情境相结合,最早可追溯到了古代钱币产生的意义,用于市场中的等价交换货物,放到今时今日的课堂,不仅增加了趣味性,也体现了人民币存在的意义,同时有效阐述了数学中的问题起源于生活。这样的导入新课,激发了学生对新知学习的兴趣,使得新课学习得以顺利进行。在课堂教学中,创设有效的情境是比较重要的,许多老师经常会利用动画来导入,刺激学生的学习,但都是一些“花边新闻”,浪费时间,毫无作用。
三、数形结合,建构模型
1.建构思维模型
乘法分配律比较抽象,是运算定律中最难理解和掌握的,在计算时学生容易出错,其根源就是学生未能从数学意义上真正理解乘法分配律。
教学片段:挖掘字母公式(a+b)×c=a×c+b×c的意义,不妨把它植入两个等宽的长方形中,通过求面积和来理解。例如:12×8+3×8=(12+3)×8。假设第一个长方形的长是12厘米,宽是8厘米,第二个长方形的长是3厘米,宽是8厘米,求两个长方形面积之和。

结合上图,可得面积之和为12×8+3×8,因为宽相等,也可以把两个长方形合并起来,长就是(12+3)厘米,宽就是8厘米,面积就是(12+3)×8。
如此一来,将抽象枯燥的公式嵌入直观形象的图形中,通过数形结合建构思维模型,把数学素材有机地整合和提升,真是简约而不简单啊!
2.建构数理模型
例如计算教学12×14=?
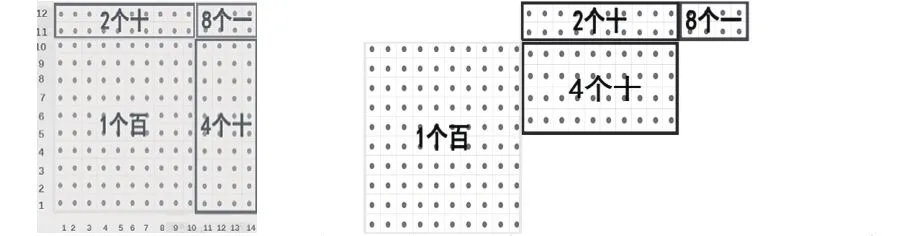
在教学两位数乘两位数时,很多人都会在课堂上纸上谈兵,反复强调它的算理:数位对齐以及要注意的事项。学生听之云里雾里,教师则不管三七二十一实行灌输式。在此处,给12乘以14建构一个分版块数理模型,分块显著,学生清楚地理解了算理,并理解了其结果在数位对齐上的含义。因此,数学中问题模型的构建,都是通过做题过程中遇到的问题总结出来的。学生在学习的过程中,只有边做题边总结这些问题的模型,才能把数学学好,只有不断夯实解题的专业能力,才能彻底避免教师的题海战术。
四、以美激乐,兴趣盎然
数学的智慧课堂中,不是枯燥乏味的。无论是运用数学本身的美去感染学生,还是教师利用教学艺术的美作用于学生,都要把学生的学习热情激发出来,让学生把数学学习当作一种欣赏美的体验。因此,教师对教材的精炼处理,语言的幽默风趣,教学过程的张弛有度,板书的简洁美观,教具的精致玲珑,教学手段的绘声绘色,教态的和蔼可亲,努力创设有效教学情境,引人入胜,让学生在学习的过程中感知美、发现美,达到“以美激乐,兴趣盎然”的精神状态。
总之,课堂应该是赋予智慧、生动形象、方法多元的。教师只有恰当地发现课堂中出现的细节,结合生活的经验建构必要的数学模型,不断提升自身的专业水平,精心设计教学过程,才能不让学生因谈数学而色变。
