动静刚度约束下客车骨架的轻量化设计*

左文杰 马洪刚 桂春阳 李行

(1.吉林大学 汽车仿真与控制国家重点实验室, 吉林 长春 130025；2.吉林大学 机械科学与工程学院, 吉林 长春 130025；3.吉林大学 汽车工程学院, 吉林 长春 130025；4.中国科学院长春光学精密机械与物理研究所 空间机器人工程中心创新研究室, 吉林 长春 130033)

动静刚度约束下客车骨架的轻量化设计*

左文杰1,2马洪刚1,3桂春阳2李行4

(1.吉林大学 汽车仿真与控制国家重点实验室, 吉林 长春 130025；2.吉林大学 机械科学与工程学院, 吉林 长春 130025；3.吉林大学 汽车工程学院, 吉林 长春 130025；4.中国科学院长春光学精密机械与物理研究所 空间机器人工程中心创新研究室, 吉林 长春 130033)

对由矩形管梁拼焊而成的客车骨架结构进行轻量化研究.首先计算了矩形管梁单元的截面特性，并定义了客车骨架的静态弯扭刚度响应与动态频率刚度响应.其次建立了客车结构优化数学模型：目标函数是车身骨架质量；设计变量是矩形管截面宽度、高度与厚度；约束是弯扭刚度与频率刚度.然后推导了响应对设计变量的灵敏度信息，并采用序列线性规划求解了该非线性优化模型.最后通过数值算例验证了该模型能在满足约束条件的前提下高效地获得轻量化的客车最优结构.

客车骨架；轻量化设计；弯扭刚度；频率刚度；优化设计

客车骨架分为非承载、半承载、全承载3种类型.全承载式车身形象地被称为“鸟笼结构”，突出特点是无明显的底盘结构，整个车身的各个构件都承受载荷，具有轻量化、高刚度、高强度的优点，是当今客车骨架设计的前沿技术.全承载客车骨架一般由矩形管拼焊而成，可由梁单元或板单元来划分网格建立客车骨架的有限元模型.梁单元构成的骨架模型求解效率高，贴近制造工艺，易于参数化，从而方便车身概念设计阶段结构优化设计，实现轻量化目标.

客车结构优化模型以整车质量为目标函数，设计变量是矩形管的截面几何尺寸，约束是静态工况下的弯扭刚度、自由模态(动态)工况下的频率刚度，因此客车结构优化是个多设计变量、多响应、多工况的结构优化问题.张大千等[1-4]对客车骨架的有限元分析和结构优化进行了系统深入的研究，如刚度优化、基于代理模型的多学科优化设计等.张代胜等[5-7]采用刚度灵敏度信息修改了车身骨架截面尺寸，实现了轻量化目的.Gauchia等[8]采用遗传算法求解了扭转刚度约束下的客车轻量化问题.那景新等[9]在刚度约束下对客车骨架的构件尺寸进行了优化设计.Torstenfelt等[10-11]研究了含有尺寸、形状、拓扑变量的车身骨架优化设计，但未考虑频率响应.

以上研究为客车设计提供了非常有意义的指导，但仍有以下难题需要解决：整车质量、弯扭静态刚度、频率动态刚度、应力强度没有一起考虑到优化模型中.此外，以上关于客车的优化设计多采用代理模型或者直接使用遗传算法等生物进化算法求解.代理模型采用试验设计采样、响应面建立函数输入输出关系，因此代理模型的精度极大地依赖于样本的选择，精度不易保证[12].生物进化算法中作为代表的遗传算法不采用梯度信息构造迭代格式，因此优化效率较低[13].对于客车骨架这样的大型工程问题，精度和效率都需要兼顾.所以文中采用基于梯度信息的序列线性规划求解动静刚度约束下的客车骨架非线性结构优化问题.

1 客车骨架有限元建模

1.1 矩形管梁单元截面特性计算

构成客车车身骨架的矩形管及其截面形状见图1，该截面共有3个设计变量：宽度b、高度h和厚度t.在设计客车骨架时，根据工艺要求，多个梁单元共用一个截面形状，也称为组件设计.由上述3个设计变量可以求得截面几何特性：横截面积A、弯曲惯性矩Iy和Iz、扭转惯性矩Ix，即

A=2t(h+b)

(1)

(2)

(3)

(4)

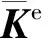
(5)

式中，T为坐标变换矩阵.组装所有矩形管梁单元的刚度矩阵和质量矩阵即可分别列出静态方程和模态方程，即

Ku=p

(6)

(7)

式中，K为总体刚度矩阵，u为由载荷向量p引起的位移向量，M为总体质量矩阵，ωi和ui分别为第i阶角频率和振型，m为模态的阶次.

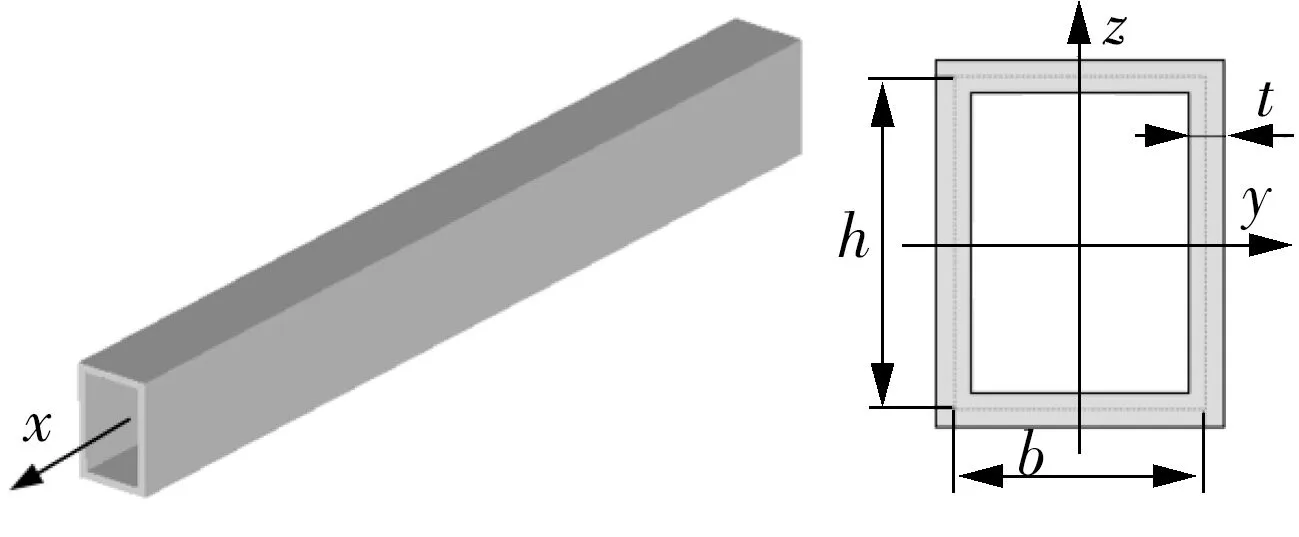
图1 矩形管梁截面及其局部坐标系Fig.1 Rectangular pipe girder section and its local coordinates

1.2 客车骨架静动态刚度定义

客车服役的最基本工况为静态弯扭工况，如图2所示.扭转工况模拟车轮越过凹坑时的单轮悬空情形，释放右前轮支撑点的所有自由度，约束左前轮支撑点Y、Z方向的平动自由度，约束左后轮支撑点X、Y、Z方向和右后轮支撑点X、Z方向的平动自由度，那么扭转刚度可以定义为

(8)

式中，MT为扭矩，Δφ为扭转角，F为集中力，B为轮距，u为由集中力F引起的位移.

弯曲工况模拟静态满载情形，那么弯曲刚度可定义为

(9)

式中，ui为由集中力Fi引起的位移，nf为集中力的数量.

客车还服役于紧急制动工况，该工况主要考核车身和悬架连接处的吊耳结构强度，不必对整车进行分析，所以文中的优化模型并未考虑该工况.

客车骨架动刚度由车身自由模态分析得到的前3阶频率来评价，其各阶频率可由式(7)计算得到.

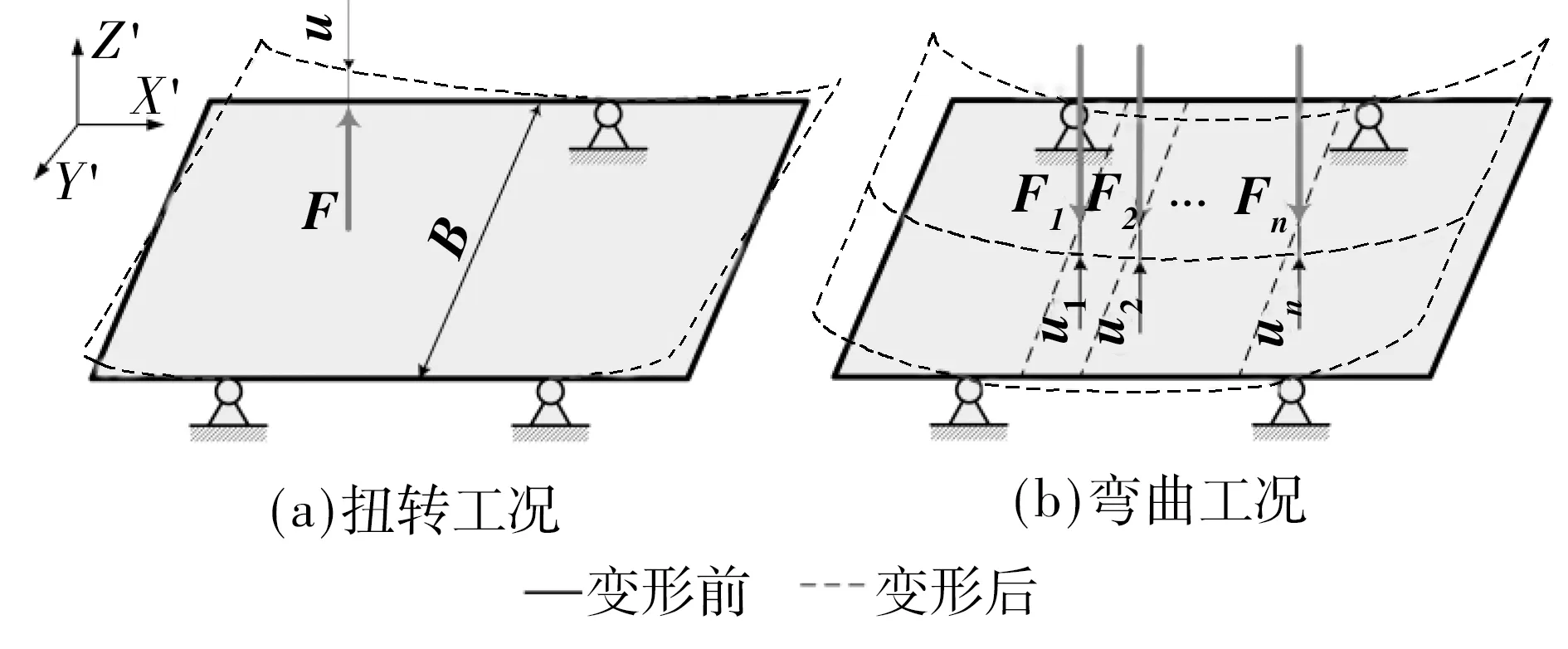
图2 工况Fig.2 Working condition

2 客车骨架优化模型及求解

2.1 结构优化数学模型

由于梁单元不能精确计算骨架接头处的应力，而板壳单元无法同时优化骨架断面3个尺寸参数，所以文中以动静刚度为约束，进行客车骨架轻量化设计，其数学模型为

(10)

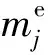
2.2 序列线性规划求解

式(10)是非线性结构优化问题，可采用基于库恩塔克(KKT)条件的准则法或者序列线性规划求解.由于式(10)约束种类和数量较多，所以序列线性规划更适合求解该问题.所以，将式(11)的目标函数与约束在指定点xl泰勒展开，取其线性项，得到如下线性规划模型：

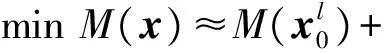
(11)

式中，上标l为循环迭代次数，为梯度符号，Δxl=x-xl，sl为第i次优化的移动限.在实际的求解过程中，当设计变量距离展开点较远时，忽略的高阶项将会引起较大的误差.为了减小误差，一个有效的方法是在每次求解线性规划时附加设计变量的移动限.一般地，移动限可取相应设计变量区间的10%.在迭代过程中，当前后两迭代步的客车质量改变量小于0.1%时，满足收敛条件.

2.3 动静刚度响应的灵敏度分析

式(11)中需要提供响应关于设计变量的梯度信息，即灵敏度.扭转刚度KT、弯曲刚度KB、频率ωi和总质量M是截面设计变量的隐函数，即

(12)

式中，x=[b1,h1,t1,…,bj,hj,tj,…,bn,hn,tn]，n为组件的数量.

将以上响应关于设计变量求导可得到

(13)

(14)

(15)

(16)

式(6)与(7)还需要求解关于设计变量的导数，将式(6)两边对设计变量xi求偏导，得

(17)

至此，扭转刚度灵敏度式(14)、弯曲刚度灵敏度式(15)、频率灵敏度式(16)都由刚度矩阵灵敏度∂K/∂xk、单元质量矩阵灵敏度∂M/∂xk来表达，该内容的推导可见文献[7]，文中不再赘述.

通过自主开发的“车身骨架优化设计软件CarFrame”实现了以上理论[15]，该软件由VB.NET语言开发完成，图形由微软DirectX渲染，主界面如图3所示.

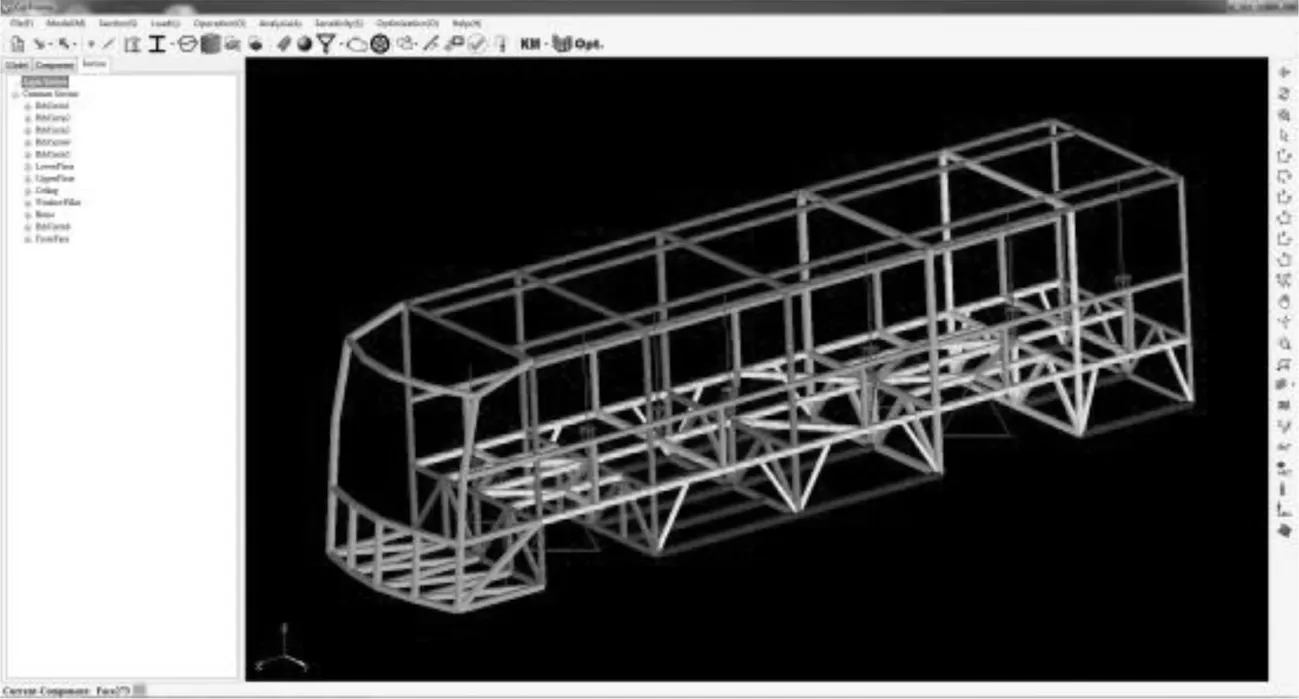
图3 自主开发的CarFrame软件主界面Fig.3 Main interface of self-developed CarFrame software

3 算例

以上模型不仅适用于矩形梁单元，也适用于槽形、Z形等截面单元[16].下面以图 4所示的全承载式客车骨架为例验证以上优化模型的有效性.该客车骨架的长度、宽度和高度分别是13.0、3.2和3.5 m.该骨架含有172个节点、333个矩形管梁单元，梁单元之间采取刚性连接方式，这些梁单元被分为12个组件，每个组件中的梁单元共用一个矩形截面，那么共有12×3=36个设计变量.

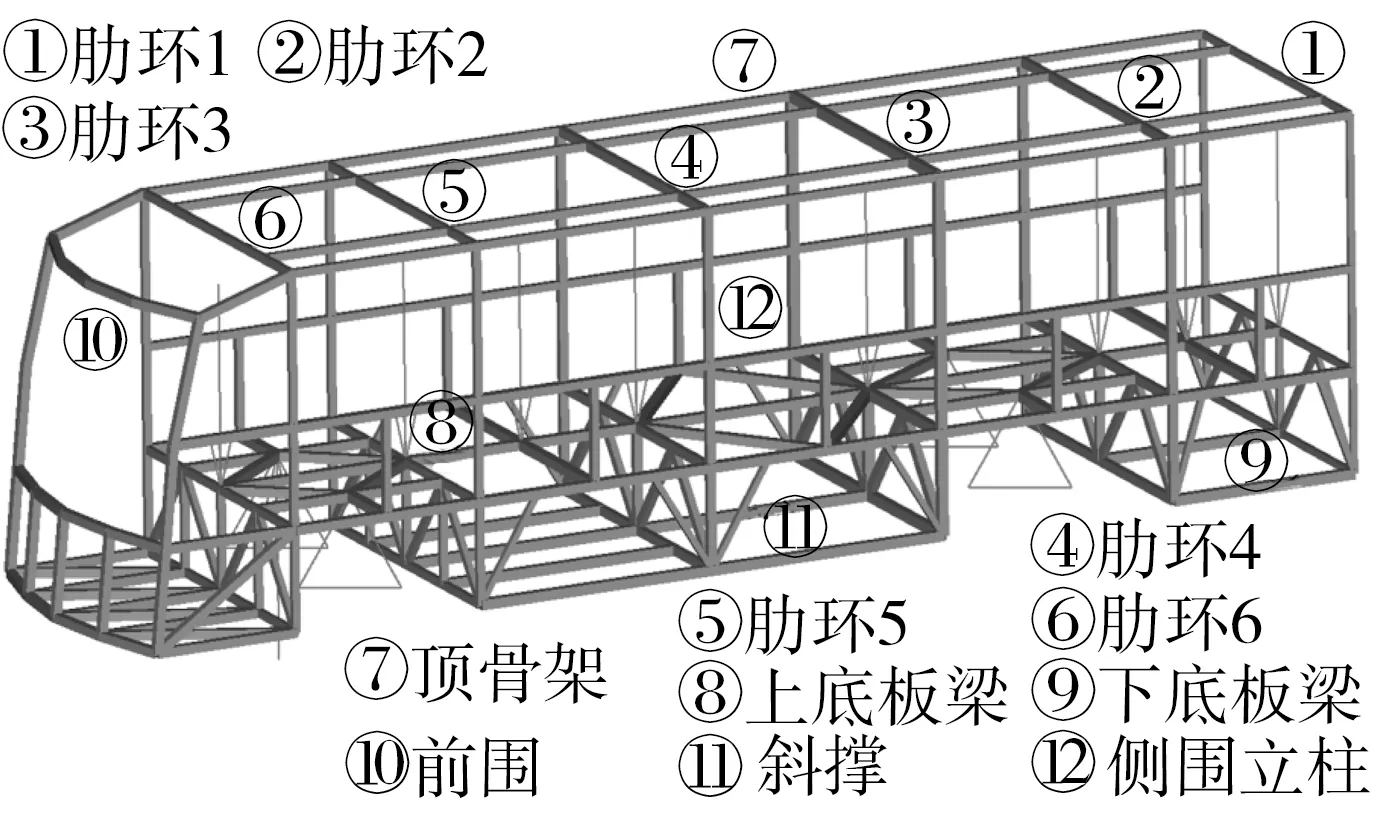
图4 全承载客车车身及其组件Fig.4 Monocoque tourist bus and its components

设计变量上下限分别为自身初始值的150%与50%，见表1.采用Intel i5 CPU、4G内存笔记本电脑进行求解，经过28 min，满足收敛条件，迭代结束.

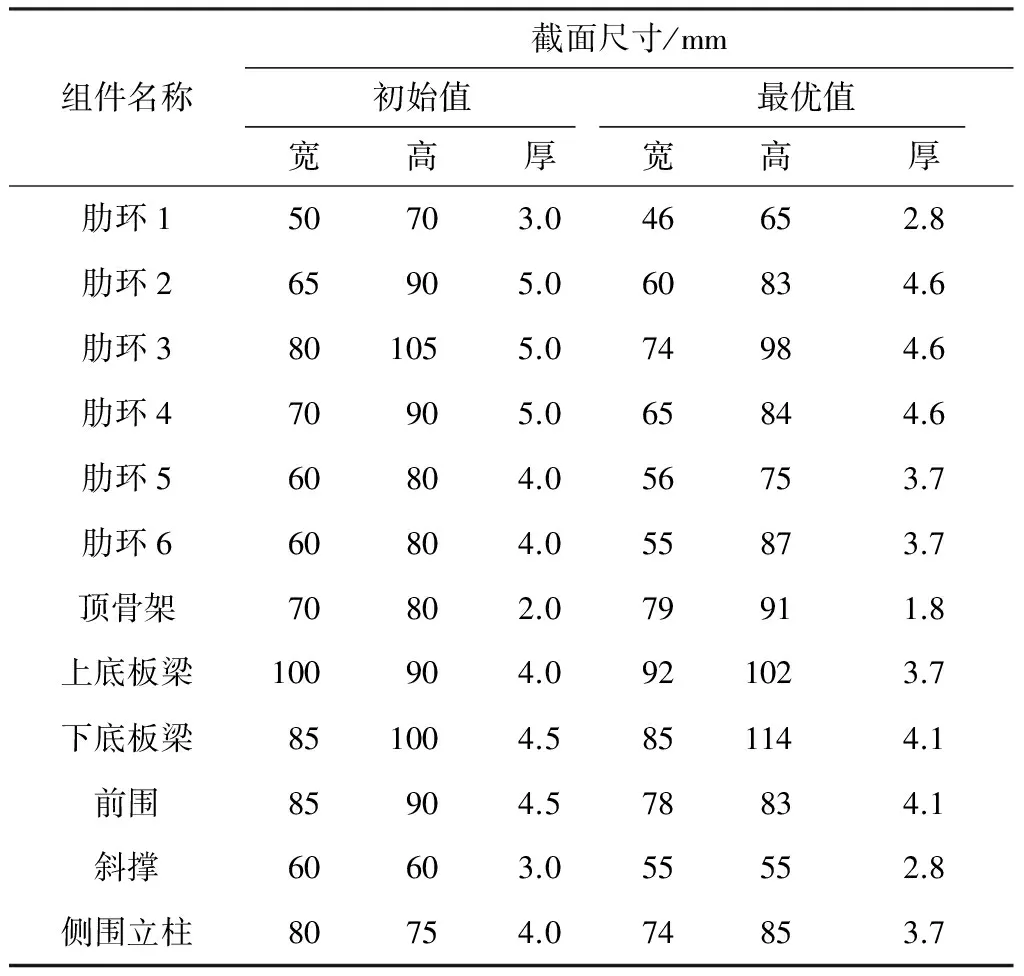
表1 客车身骨架截面尺寸对比Table 1 Comparison of cross-sectional sizes of bus frame

优化前和优化后的客车骨架扭转刚度灵敏度如图5(a)、5(b)所示.优化后的灵敏度相比于优化前基本都得到了提升，说明优化后的客车骨架扭转刚度对设计变量极其敏感，可修改余地已经不大；相反，初始的客车骨架的扭转刚度灵敏度较低，减小截面尺寸变量不会大幅降低扭转刚度，所以初始客车骨架的设计裕度较大.

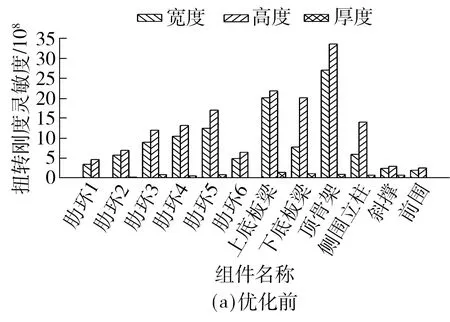
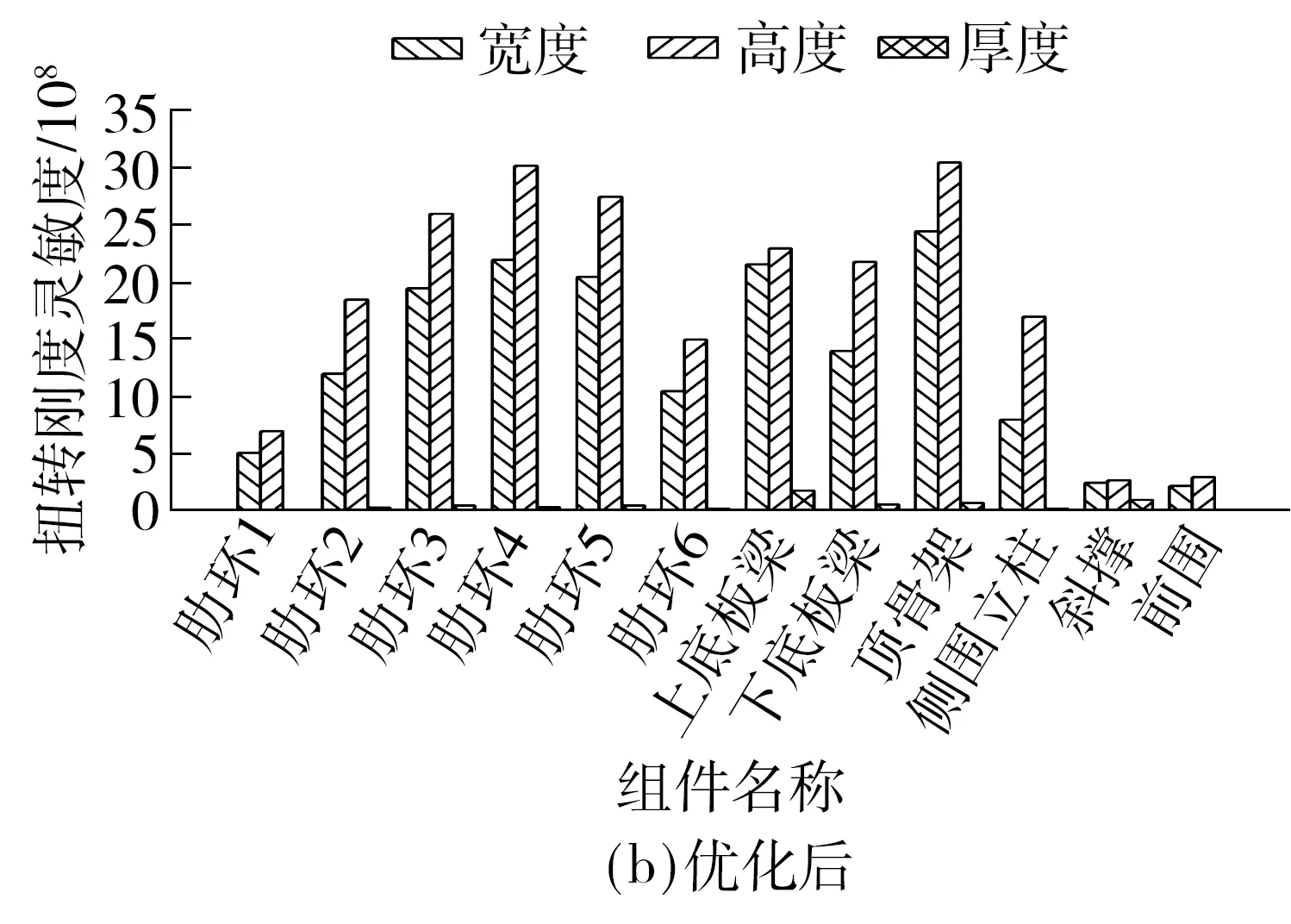
图5 扭转刚度灵敏度Fig.5 Torsional stiffness sensitivity

由图6可见，客车骨架质量持续降低，但是弯扭刚度、频率刚度并未降低，见图7、8，从而可以获得高刚度、轻量化的客车骨架结构.客车骨架初始值与最优值对比见表2.

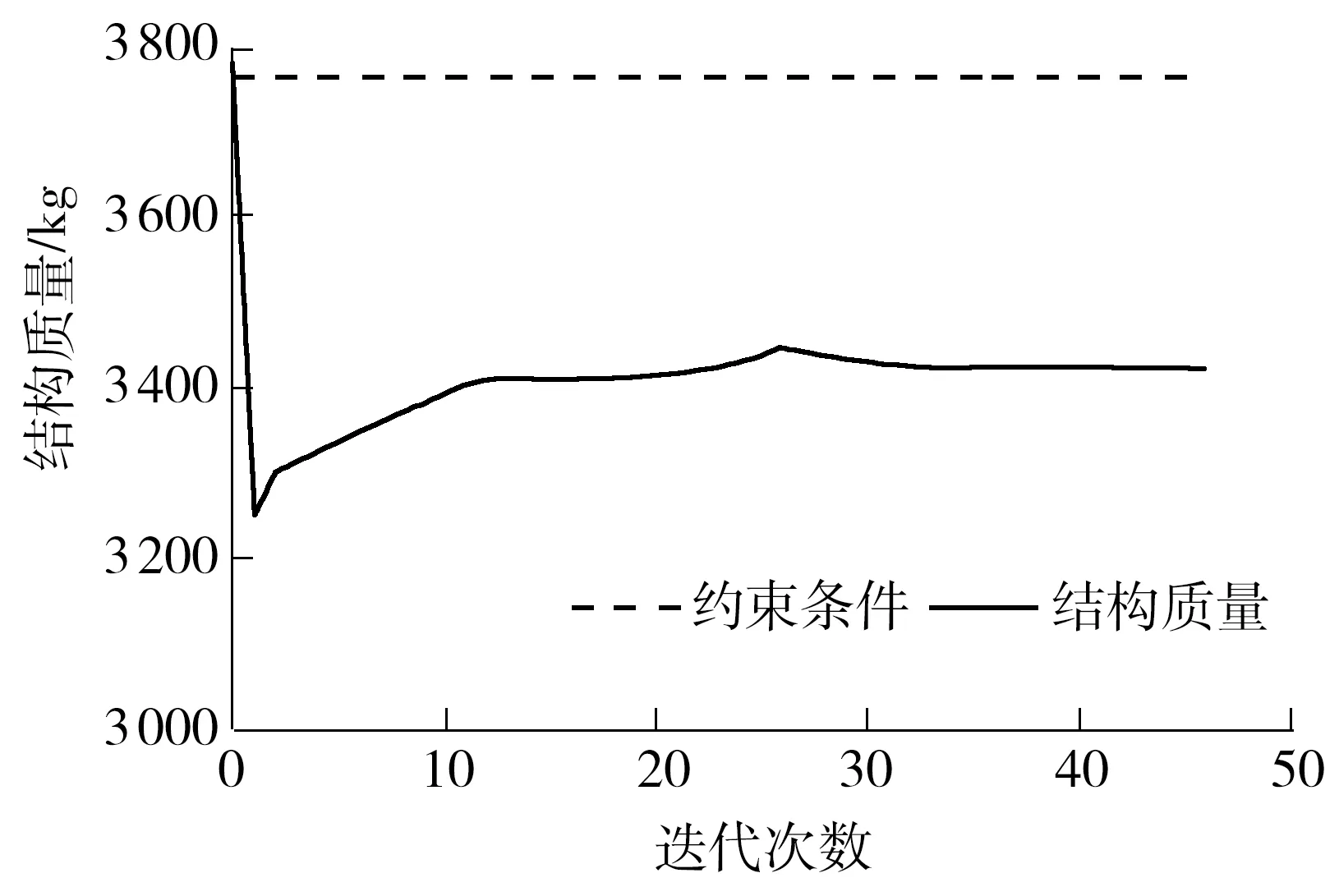
图6 迭代过程中的客车车身骨架质量Fig.6 Structural mass of bus body frame in the iterative process

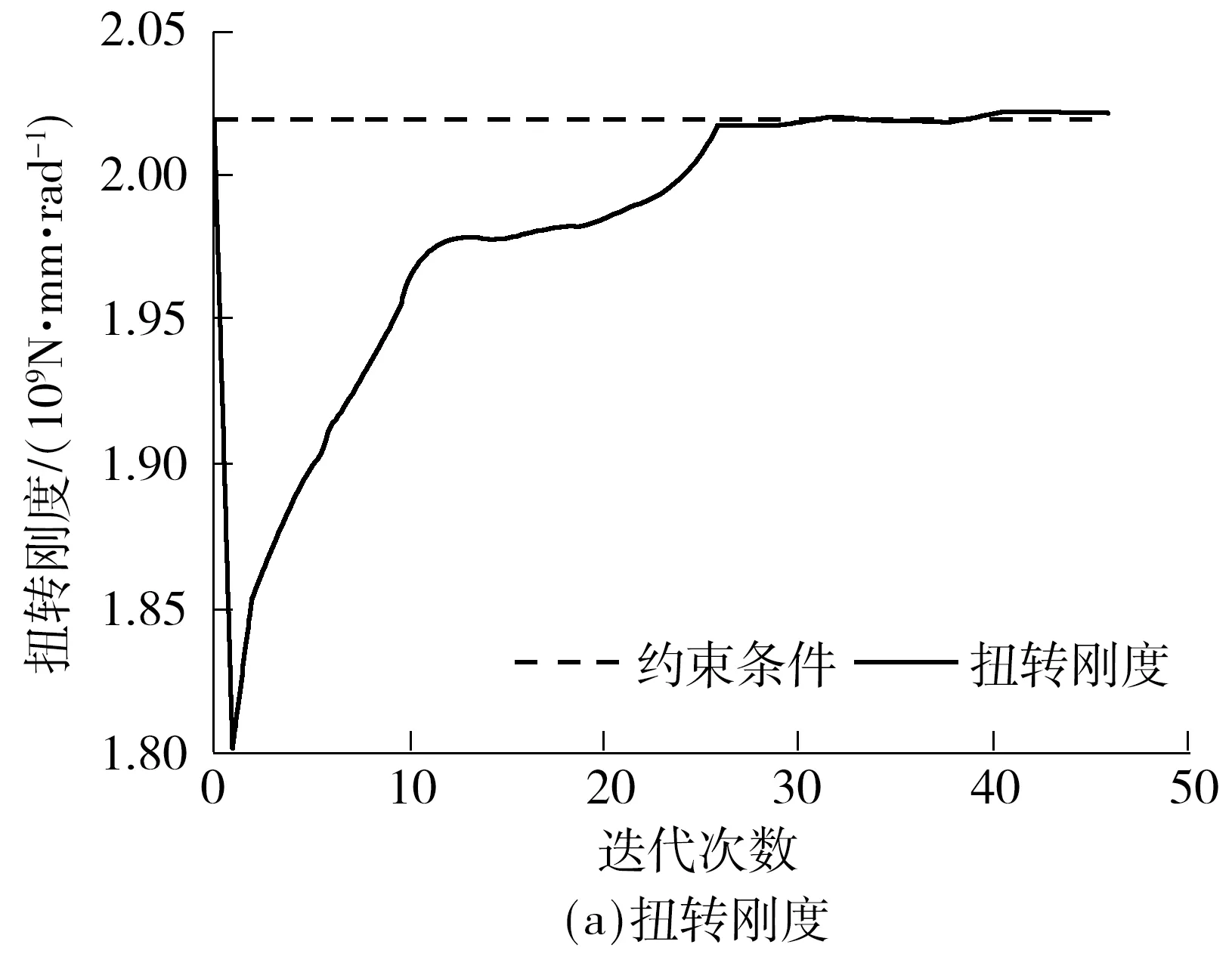
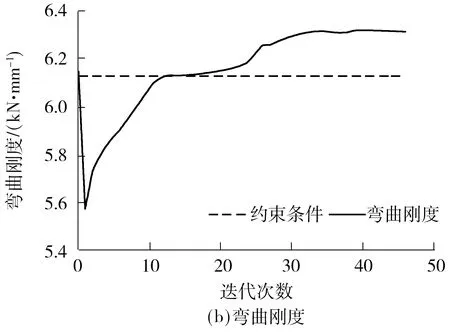
图7 迭代过程中的扭转和弯曲刚度Fig.7 Torsional and bending stiffness in the iterative process

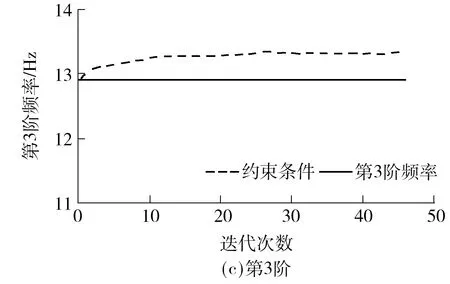
图8 迭代过程中的频率Fig.8 Frequency in the iterative process

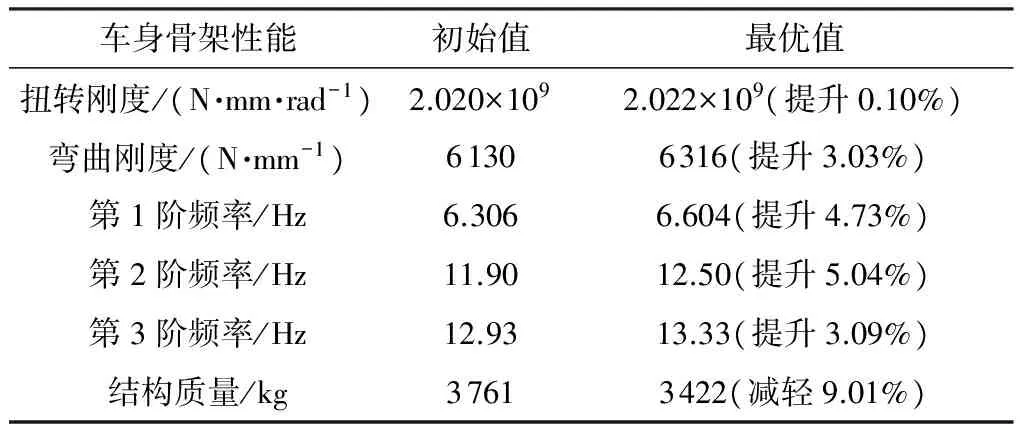
表2 客车骨架性能对比Table 2 Comparison of bus frame performance

4 结语

文中在静动态刚度约束下对矩形管构成的客车骨架进行了轻量化设计.为满足制造工艺采用了组件化设计方法，即同一个组件中的矩形管共用一个截面设计变量.对弯曲刚度、扭转刚度与频率刚度进行了灵敏度分析，采用序列线性规划方法求解了非线性结构优化问题.通过算例可以看到客车骨架质量大幅减轻，扭转刚度、弯曲刚度和前3阶频率均有一定的提升，达到高刚度、轻量化的目的.算例中的客车骨架有36个设计变量、333个梁单元，在Intel i5 CPU的笔记本电脑上只需28 min即可完成优化，验证了基于梯度信息的结构优化方法的高效性.

[1] 张大千,张天侠,张国胜,等.基于灵敏度分析的客车车身骨架轻量化设计 [J].机械强度,2011,33(6):913-920.

ZHANG Da-qian,ZHANG Tian-xia,ZHANG Guo-sheng,et al.Lightweight design for bus body frame based on sensitivity analysis [J].Journal of Mechanical Strength,2011,33(6):913-920.

[2] 陈吉清,黄信宏,周云郊,等.钢铝混合汽车前纵梁的耐撞性优化方法比较 [J].华南理工大学学报(自然科学版),2012,40(7):90-94.

CHEN Ji-qing,HUANG Xin-hong,ZHOU Yun-jiao,et al.Comparison of crashworthiness optimization methods of steel-aluminum hybrid automotive front rail [J].Journal of South China University of Technology(Natural Science Edition),2012,40(7):90-94.

[3] 苏瑞意，桂良进，吴章斌，等.大客车车身骨架多学科协同优化设计 [J].机械工程学报,2010,46(18):128-133.

SU Rui-yi,GUI Liang-jin,WU Zhang-bin,et al.Multidisciplinary design and collaborative optimization for bus body [J].Journal of Mechanical Engineering,2010,46(18):128-133.

[4] 丁炜琦,田程,范子杰.基于代理模型的大客车结构动态特性多目标优化 [J].汽车工程,2012,34(12):1072-1075.

DING Wei-qi,TIAN Cheng,FAN Zi-jie.Multi-objective optimization on the dynamic characteristics of bus structure based on surrogate Model [J].Journal of Automobile Engineering,2012,34(12):1072-1075.

[5] 张代胜，张林涛，谭继锦，等.基于刚度灵敏度分析的客车车身轻量化研究 [J].汽车工程,2008,30(8):718-720.

ZHANG Dai-sheng,ZHANG Lin-tao,TAN Ji-jin,et al.A research on the lightweighting of bus body based on stiffness sensitivity analysis [J].Journal of Automobile Engineering,2008,30(8):718-720.

[6] ZUO W.Bi-level optimization for the cross-sectional shape of thin-walled car body frame constrained with static and dynamic stiffness [J].Proc IMechE Part D:Journal of Automobile Engineering,2015,229(8):1046-1059.

[7] CHEN W,ZUO W.Component sensitivity analysis of conceptual vehicle body for lightweight design under static and dynamic stiffness demands [J].International Journal of Vehicle Design,2014,66(2):107-123.

[8] GAUCHIA A,DIAZ V,BOADA M J L,et al.Torsional stiffness and weight optimization of a real bus structure [J].International Journal of Automotive Technology,2010,11(1):41-7.

[9] 那景新,高剑峰.基于局部搜索和整体优化的客车杆件截面参数正向设计 [J].吉林大学学报(工学版)2014,44(6):1564-1570.

NA Jing-xin,GAO Jian-feng.Top-down design method based on local search and global optimization for cross-sectional size of bus body [J].Journal of Jilin University(Engineering and Technology Edition),2014,44(6):1564-1570.

[10] TORSTENFELT B,KLARBRING A.Structural optimization of modular product families with application to car space frame structures [J].Structural and Multidisciplinary Optimization,2006,32(2):133-140.

[11] TORSTENFELT B,KLARBRING A.Conceptual optimal design of modular car product families using simultaneous size,shape and topology optimization [J].Finite Ele-ments in Analysis and Design,2007,43(14):1050-1061.

[12] SIGMUND O.On the usefulness of non-gradient approaches in topology optimization [J].Structural and Multidisciplinary Optimization,2011,43(5):589-596.

[13] 杨荣山,黄向东,袁仲荣,等.多目标优化方法在悬架几何设计上的应用 [J].华南理工大学学报(自然科学版),2009,37(7):85-89.

YANG Rong-shan,HUANG Xiang-dong,YUAN Zhong-rong,et al.Application of multi-objective optimization methods to geometric design of suspension [J].Journal of South China University of Technology(Natural Science Edition),2009,37(7):85-89.

[14] 王勖成.有限单元法 [M].北京:清华大学出版社,2003.

[15] 左文杰.汽车车身骨架轻量化与高刚度灵敏度分析软件:2013SR108676 [P],2013-09-18.

[16] ZUO W J,BAI J T.Cross-sectional shape design and optimization of automotive body with stamping constraints [J].International Journal of Automotive Technology,2016,17(6):1003-1011.

s:Supported by the National Natural Science Foundation of China(51575226) and the Plan for Scientific and Technological Development of Jilin Province(20140101071JC)

LightweightDesignofBusFrameConstrainedbyStaticandDynamicStiffness

ZUOWen-jie1,2MAHong-gang1,3GUIChun-yang2LIHang4

(1. State Key Laboratory of Automotive Simulation and Control, Jilin University, Changchun 130025, Jilin, China;2. College of Mechanical Science and Engineering, Jilin University, Changchun 130025, Jilin, China;3. College of Automotive Engineering, Jilin University, Changchun 130025, Jilin, China;4. Changchun Institute of Optics, Fine Mechanics and Physics, Chinese Academy of Sciences, Changchun 130033, Jilin, China)

In order to achieve a lightweight structure of the bus frame consisting of rectangular tubes, first, the cross-sectional properties of the rectangular tubes are calculated, and the responses of static bending stiffness, static torsional stiffness, and dynamic frequency stiffness are respectively defined. Next, a structural optimization model of the bus frame is constructed. In the model, the objective function is the structural mass, the design variables are the cross-sectional breadth, height, and thickness of the rectangular tubes, and the constraints are the bending, torsional and frequency stiffness. Then, the sensitivity information of the responses with respect to the design variables is derived, and the nonlinear optimization model is solved through the sequential linear programming. Finally, by a numerical example, it is proved that the proposed method can efficiently acquire the optimal bus frame that satisfies the constraint conditions.

bus frame; lightweight design; bending and torsional stiffness; frequency stiffness; structural optimization

2016-09-27

国家自然科学基金面上项目(51575226)；吉林省科技发展计划项目(20140101071JC)

左文杰(1981-)，男，博士，副教授，主要从事汽车结构轻量化研究.E-mail:zuowenjie@jlu.edu.cn

1000-565X(2017)08-0007-06

U 463.822

10.3969/j.issn.1000-565X.2017.08.002