半主动阻尼拉杆的动态特性研究*

王道勇 赵学智 上官文斌,† 叶必军

(1.华南理工大学 机械与汽车工程学院，广东 广州 510640；2.宁波拓普集团股份有限公司，浙江 宁波 315800)

半主动阻尼拉杆的动态特性研究*

王道勇1赵学智1上官文斌1,2†叶必军2

(1.华南理工大学 机械与汽车工程学院，广东 广州 510640；2.宁波拓普集团股份有限公司，浙江 宁波 315800)

将半主动阻尼拉杆等效成质量和弹簧的二自由度模型，推导了动刚度表达式.建立了基于线弹性、分数导数和摩擦模型的橡胶衬套非线性模型，采用Maxwell模型来描述广义阻尼器动刚度.利用最小二乘法对衬套和广义阻尼器动刚度模型中的参数进行了识别.通过实验和仿真计算对比了半主动阻尼拉杆在通电和不通电两种工况下的动刚度值.分析了等效弹簧刚度、阻尼常数和衬套刚度对半主动阻尼拉杆动刚度和阻尼性能的影响.结果表明:当衬套刚度、等效弹簧刚度和阻尼常数较大时，半主动阻尼拉杆的动刚度较大;增加阻尼常数能提高半主动阻尼拉杆低频时的动刚度，降低等效弹簧刚度和衬套刚度可以减小高频时的动刚度;衬套刚度对阻尼性能影响较小;等效弹簧刚度和阻尼常数越小，半主动阻尼拉杆阻尼性能越好.

半主动阻尼拉杆；动刚度；阻尼性能

半主动阻尼拉杆是一种通过汽车行车电脑控制电磁阀的开或关来实现流道切换，以达到不同阻尼效果的液压减振元件，其结构与液压减振器类似.它主要用于动力总成悬置系统中，为汽车起停、原地换挡等瞬态工况下提供大阻尼，衰减动力总成的冲击，降低车内振动.其工作原理为：当汽车处于起停、原地换挡等特殊工况时，电磁阀通电，外通道关闭，油液主要从运动活塞上的阻尼孔流动，产生大阻尼；当汽车处于怠速和稳态工况时，电磁阀断电，油液主要从旁通流道流动，产生较小的阻尼.其动特性具有随着激振频率和激振振幅而变的特性.阻尼系数和动刚度一般是液压减振元件的两个重要参数，获得半主动阻尼拉杆的阻尼系数和动刚度，对其隔振性能的研究和在动力总成悬置系统中的动态响应计算有非常重要的作用和意义.

目前国内外有关液压减振元件的动刚度和阻尼特性的报道中，以液阻悬置和液压衬套居多[1-4]，对液压减振器动刚度的研究较少.Kowalski等[5]通过实验分别研究了液压减振器在单一正弦波、两种不同的正弦波和随机激励下，减振器动刚度和阻尼系数的变化规律.Sonnenburg等[6]分析了等效弹簧刚度(由缸筒和油液表征)及阻尼常数(液压减振器在某一恒定振幅激励下，随频率变大，阻尼系数不再变化)对液压减振器有效阻尼系数的影响，文中将衬套的动刚度看作常数，忽略了衬套动刚度的频率相关性和振幅相关性.

文中将半主动阻尼拉杆等效成质量单元和刚度单元，建立半主动阻尼拉杆的二自由度模型.在推导其动刚度的基础上，通过建立基于线弹性、分数导数和摩擦模型的衬套动态特性模型，采用Maxwell模型表征广义阻尼器单元(由产生阻尼的运动活塞和缸筒内的液压油组成)的动态特性，由此确立半主动阻尼拉杆的动刚度.将仿真得到的阻尼拉杆的动刚度值与实验结果对比，结果吻合良好.同时分析了各个因素对半主动阻尼拉杆动刚度和阻尼性能的影响.

1 半主动阻尼拉杆的动刚度建模

半主动阻尼拉杆主要由缸体、电磁阀、活塞杆及两端橡胶衬套组成，见图1.液压油分布在运动活塞两侧.当活塞杆受到外激励时，油液通过运动活塞上的小阻尼孔或外通道流动产生阻尼.浮动活塞与缸体右侧形成的密闭空间一般充入0.5～0.8 MPa的氮气，主要作用是提供体积补偿，防止出现空程畸变.

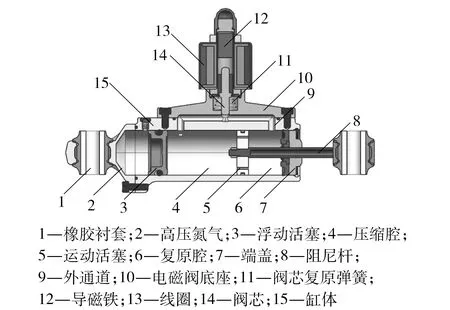
图1 半主动阻尼拉杆实物Fig.1 Semi-active hydraulic damper strut

阻尼拉杆各部分零件的相关参数如表1所示.

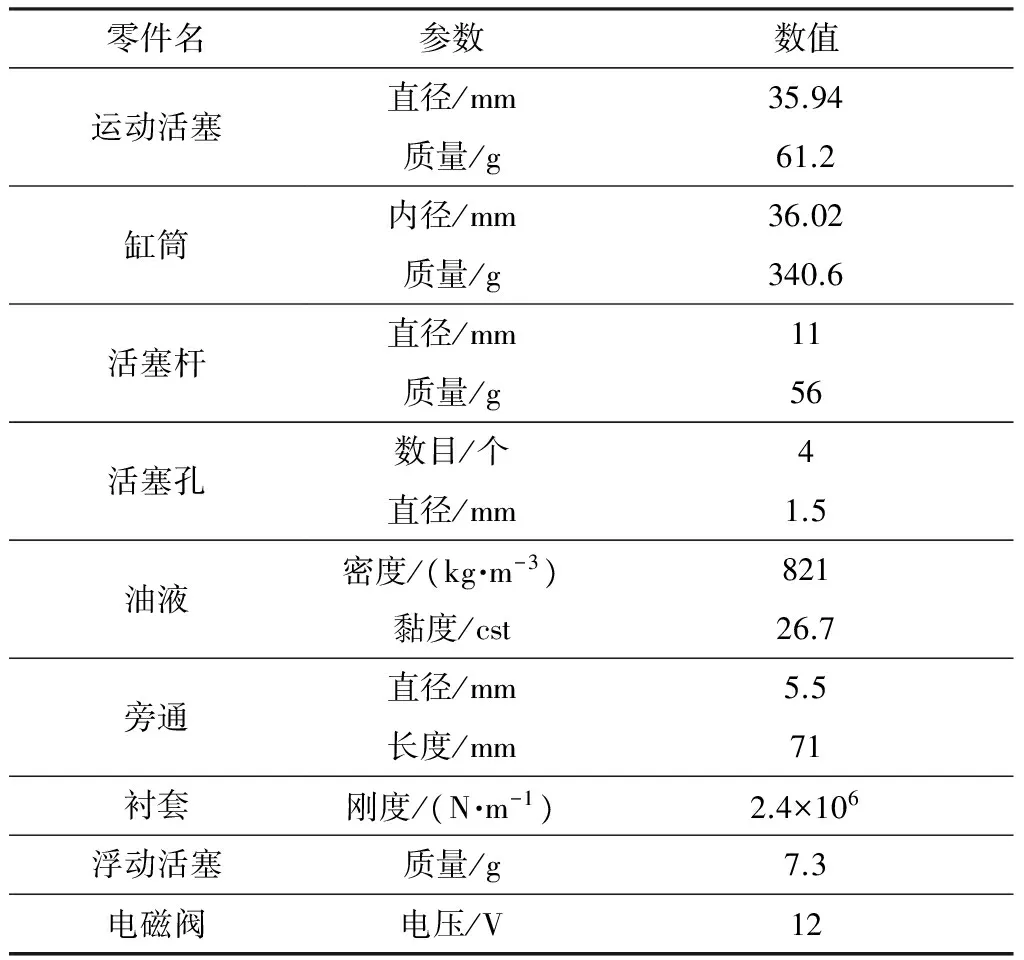
表1 半主动阻尼拉杆参数Table 1 Parameters of semi-active damping strut

通过图1可知，半主动阻尼拉杆可以看成是包含质量单元、弹簧单元和阻尼单元的元件，因此，为方便问题的分析，将图1中的半主动阻尼拉杆等效成包含质量和弹簧单元的二自由度模型，如图2所示.

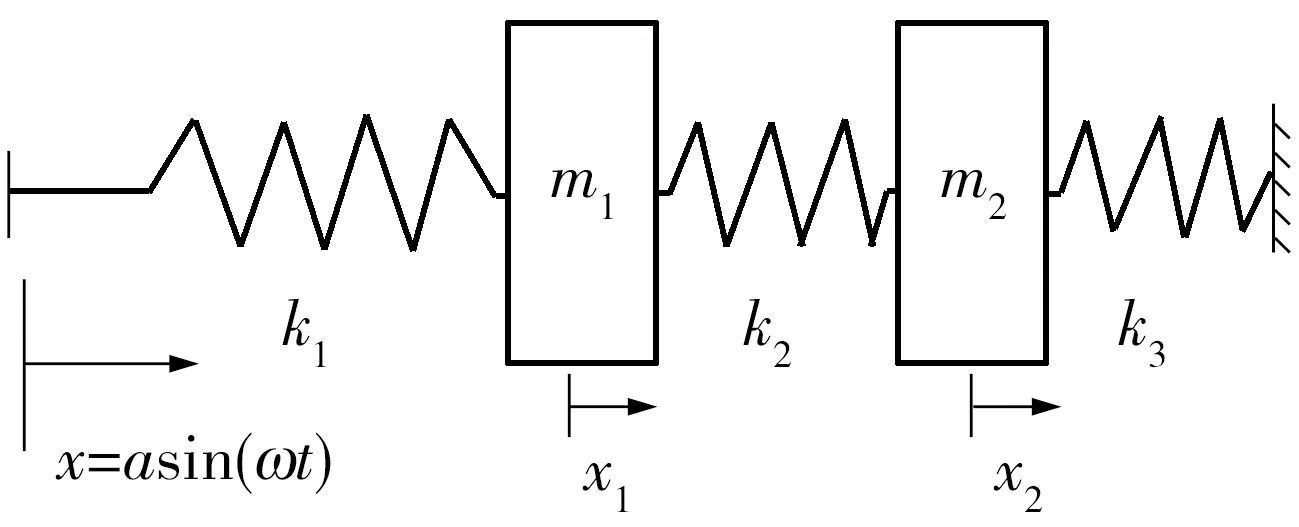
图2 半主动阻尼拉杆的二自由度模型Fig.2 2-DOF model of semi-active damping rod

图2中，m1为活塞杆的质量，m2为缸筒的质量，k1和k3分别为衬套的复刚度，k2为广义的阻尼器单元的复刚度.图2的振动方程可写为

(1)

衬套1和3分别连接动力总成和副车架，因此在发动机端的激励下，通过半主动阻尼拉杆传递到副车架的力为

F=k3(ω)x2=kdynx

(2)

由式(1)拉普拉斯变换，与式(2)联立可得到半主动阻尼拉杆的动刚度为

(3)

由于缸筒m2的固有频率较大，在频率为1～200 Hz范围内可以近似为刚体，同时半主动阻尼拉杆在实际运动过程中，缸筒一般处于静止状态.因此把半主动阻尼拉杆简化成广义阻尼器-活塞杆-衬套的模型(如图3所示)，半主动阻尼拉杆的简化模型和简化后的动刚度分别用图3和式(4)表示.

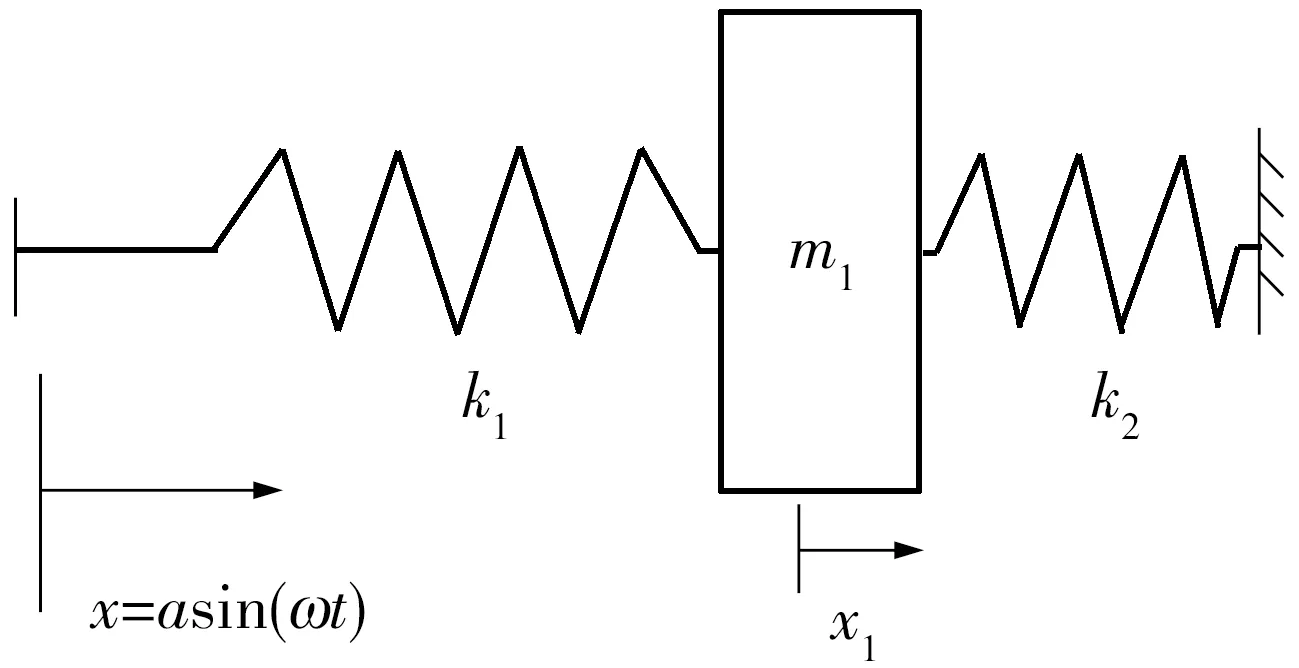
图3 简化的动刚度模型Fig.3 Simplified dynamic stiffness model

(4)

1.1 橡胶衬套的动刚度模型

橡胶衬套的动态特性具有很强的非线性，它与预载、激振振幅、激振频率和环境温度等因素相关.衬套在外界载荷作用下受到的力可以表示为3个分力的叠加，即

F=Felast+Ffrict+Ffreq

(5)

式中,Felast、Ffrict和Ffreq分别为弹性恢复力、摩擦力和粘弹性力.文中基于橡胶衬套的动态特性实验，建立基于线弹性、分数导数和摩擦模型的橡胶衬套的非线性模型[7-8]，如图4所示.Kelast为线弹性刚度，α为任意分数导数阶数，b为粘性阻尼系数，Ffmax为最大摩擦力，位移x2为从摩擦力-位移迟滞环上参考点(xs，Ffs)=(0，0)开始，当摩擦力Ffric=Ffmax/2时的位移.

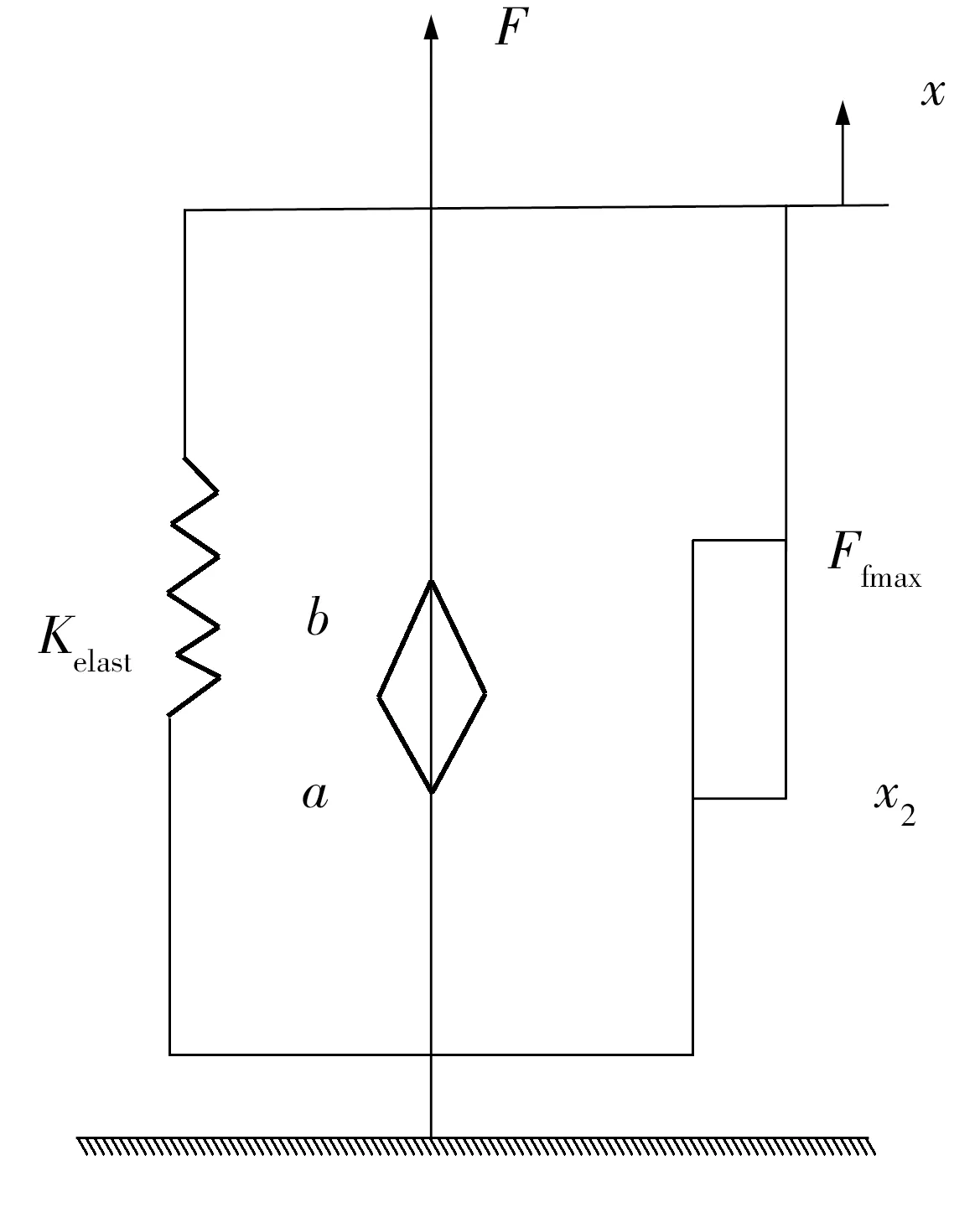
图4 橡胶衬套的动刚度模型Fig.4 Dynamic stiffness model of rubber bushing

1.1.1 线弹性模型

文中用线弹性模型来描述弹性恢复力，弹性恢复力Felast为

Felast=Kelastx(t)

(6)

式中，Kelast对应衬套的线弹性力学行为.

1.1.2 摩擦模型

文中采用摩擦模型来描述振幅相关性，Berg单元参数识别简单，能准确地描述橡胶件的振幅相关性.模型中共有两个参数Ffmax和x2，摩擦力Ffric用下述分段函数定义[9-10]：

(7)

1.1.3 粘弹性分数导数模型

为更好地描述橡胶衬套的动特性的频率相关性，引入分数导数模型，方便在更宽的频率范围描述橡胶减振元件等粘弹性材料随频率变化的特性.分数导数最常用的定义由Reimann-Liouville积分给出:

(8)

式中各参数物理意义见文献[3]，对于粘弹性材料，0≤α<1，方程(8)可简化为

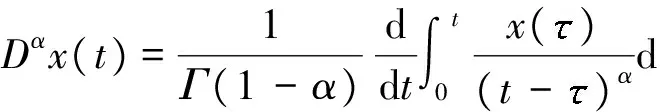
(9)

橡胶衬套动特性分析模型中，粘弹性力Ffreq与位移的关系用下式来表示：

Ffreq=bDαx(t)

(10)

式中，Dαx(t)指x(t)对时间t求α阶导数，0≤α<1.

1.2 广义阻尼器单元的动刚度

广义阻尼器单元的动刚度主要由缸筒和液压油表征.一般在描述液压减振元件的动刚度模型中，Kelvin-Voigt模型和Maxwell模型被广泛地应用.相比于Kelvin-Voigt模型，Maxwell模型能更好地描述液体的流变特性[11]，在低频范围内能很好地表征减振元件的动态特性[12].Maxwell模型所描述的动刚度由一个阻尼元件和一个弹性元件串联组成，如图5所示.

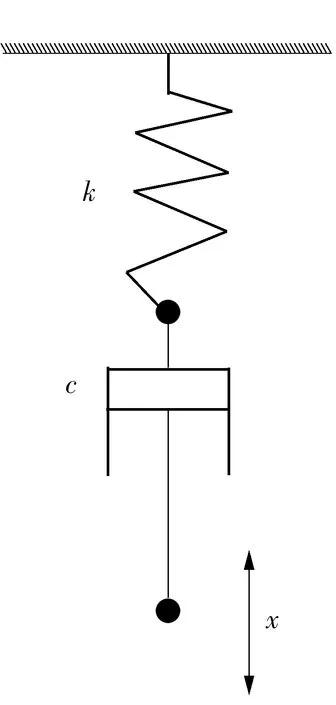
图5 Maxwell模型Fig.5 Maxwell model

针对文中的广义阻尼器单元，阻尼常数由Maxwell中的阻尼元件c表示，油液和缸筒表征的等效弹簧刚度用弹性元件k表示.动刚度与阻尼常数、等效弹簧刚度及激振频率的关系可以写为

(11)

等效弹簧刚度可表示为[13]

(12)

(13)

(14)

式中，Dcy1为缸筒直径，dcy1为缸筒的厚度，Vcy1为缸筒的总体积，Voil为油液的体积，E为缸筒材料的弹性模量，Koil为油液的弹性体积模量，ω为激振圆频率.

2 参数识别

2.1 衬套弹性单元和摩擦单元参数识别

为表征弹性单元和摩擦单元的参数，在进行摩擦力模型的参数识别时，采用橡胶衬套在低频、大振幅时的动态测试数据.由于实验频率很低(f=0.01 Hz)，实验数据中含有的粘弹性力成分可以忽略不计，因此可以近似地认为它只含有弹性恢复力和摩擦力.

图6为频率为0.01 Hz、振幅为1 mm时的力-位移曲线图.

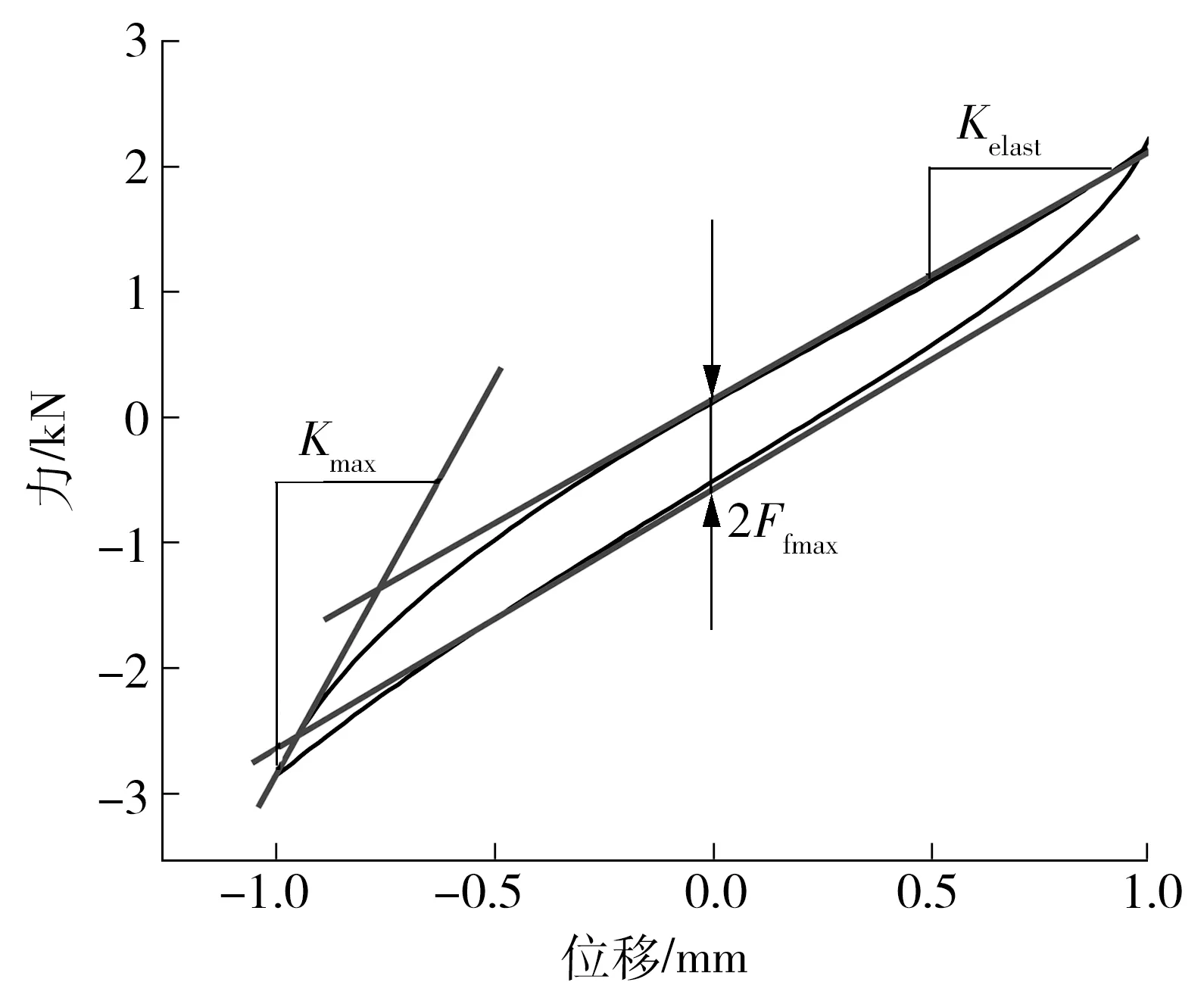
图6 低频简谐激励下的力-位移关系Fig.6 Force-displacement relation at low-frequency sine excitation

由图6可知，在位移接近极限位移时，曲线的斜率即为衬套的线性刚度Kelast.为确定最大摩擦力Ffmax，在复原和压缩段，分别将接近极限位移处曲线的两条切线延长，由激励位移的对称性可知两条切线间的竖直距离近似等于2Ffmax.在曲线复原和压缩过渡点处的斜率得到最大的Kmax.识别结果如表2所示.

表2 弹性单元和摩擦单元的识别结果Table 2 Identification results of elastic and frictional elements

(15)

将表2识别结果代入方程(15)，计算得到x2为0.09 mm.

2.2 衬套粘性单元的参数识别

在识别分数导数模型单元中的参数b和α时，选用频率为0～50 Hz、振幅为0.05 mm的激励，测得橡胶衬套的复刚度.在进行分数导数模型参数拟合时，为减小摩擦力的影响，需从测量的复刚度值中将摩擦力表征的一部分刚度去除.

根据2.1节中拟合得到的参数Ffmax和x2，计算出在激励振幅为x0时的摩擦力Ffric0为

(16)

在橡胶衬套动刚度中，摩擦力表征的刚度写为

(17)

根据Kari[14]提及的方法，对式(10)进行傅里叶变换，可以得到

Ffieq(ω)=bDαx(ω)=b(iω)αx(ω)

(18)

根据式(15)、(16)计算可得小振幅0.05 mm激励下的摩擦力Ffrict0=79 N，Kfrict=1 578 N/mm.利用最小二乘法识别得到参数值b=53.45 N·sα/mm,α=0.39.

因此橡胶衬套的动刚度的表达式为

k1(ω)=Kelast+Kfrict+Kfreq=3 360+53.45(iω)0.39

(19)

2.3 广义阻尼器单元参数识别

半主动阻尼拉杆的物理参数如表3所示.

联立方程(11)-(14)和表3中半主动阻尼拉杆的几何参数，可以识别出半主动阻尼拉杆的等效弹簧刚度k为2.15×106N/m.

半主动阻尼拉杆的阻尼系数是在不同加载(频率和振幅)条件下，通过MTS831台架测试获得.图7为通电和不通电下的阻尼系数，可知在不通电时，其阻尼系数随频率变小，最终保持不变.在通电时，阻尼系数随频率先变小，后变大，最终保持不变.

表3 半主动阻尼拉杆的几何参数Table 3 Geometric parameters of semi-active damping rod

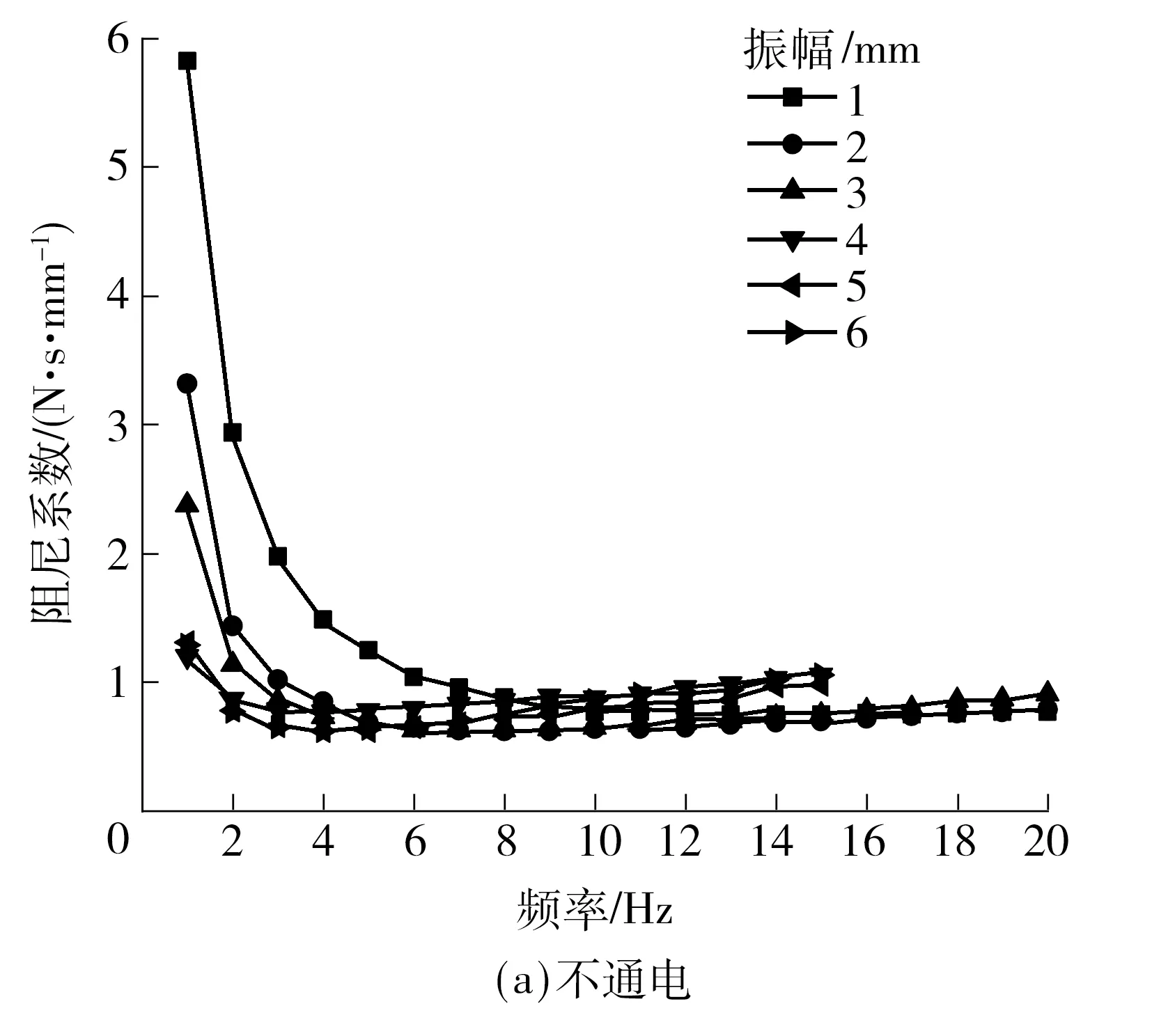
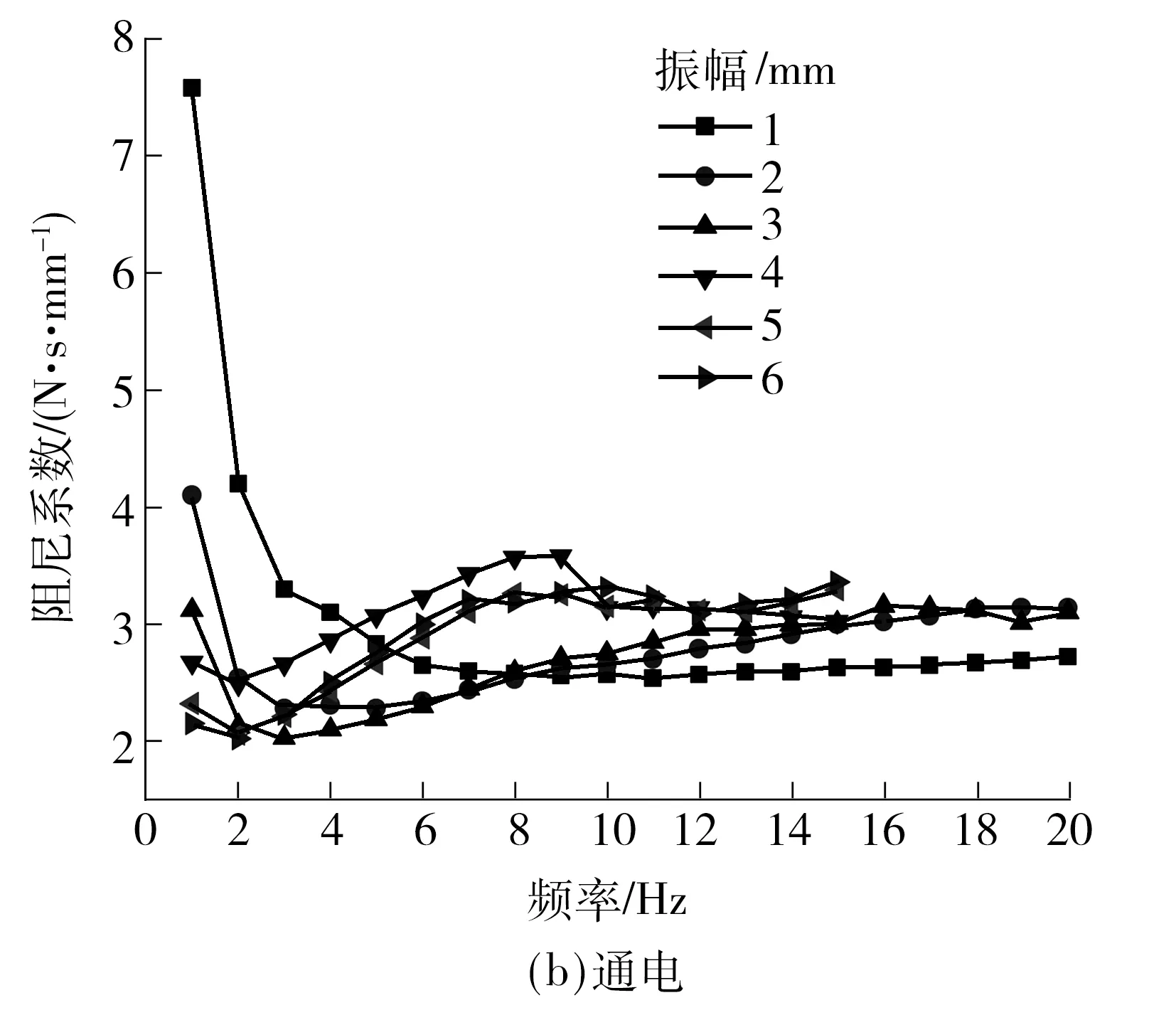
图7 不通电/通电时半主动阻尼拉杆的阻尼系数Fig.7 Damping coefficient of semi-active damping rod in power on/off condition

3 实验验证

为验证文中动刚度模型的正确性，在MTS831试验台架上对半主动阻尼拉杆在通电和不通电两种情况下的动刚度进行了测试，如图8所示.其中半主动阻尼拉杆两端衬套通过双头螺杆分别与上、下U型工装相连.阻尼拉杆上的电磁阀与12 V直流电源连接，用于测试阻尼拉杆通电和断电下的动刚度.拉杆随着与上U型工装相连的MTS作动器上、下运动.测试结果如图9所示.

图8 半主动阻尼拉杆动特性实验Fig.8 Dynamic characteristic experiment of semi-active HDS

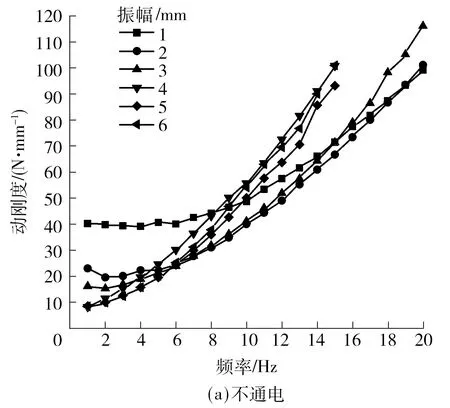
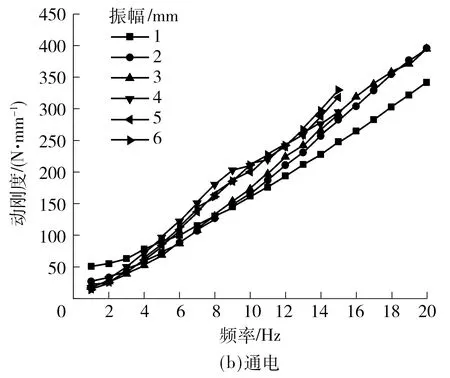
图9 不通电/通电时半主动阻尼拉杆的动刚度Fig.9 Dynamic stiffness of semi-active HDS in power on/off condition

由图9可知，在低频范围内，半主动阻尼拉杆的动刚度随频率呈类似线性增加，大振幅下的动刚度值大于同频率小振幅动刚度值.通电下的动刚度明显大于不通电下的动刚度.

根据第2节中识别的半主动阻尼拉杆各参数，计算了通电和不通电情况下小振幅为1 mm和大振幅为4 mm的动刚度值，并与实验测试值进行了对比.

定义相对误差为实测动刚度值与计算动刚度值的绝对值之差与实测动刚度的比值.通过图10中实验和计算对比可知：在通电时，小振幅1 mm和大振幅4 mm下的计算值和实测动刚度值相对误差较小，吻合度较高；不通电时，振幅为4 mm的计算值和实测动刚度吻合良好，5 Hz以后相对误差逐渐减小，10 Hz以后相对误差在20%以内.振幅为1 mm时的计算值和实测值在10 Hz以下有明显的差异，是由于运动位移小，通过运动活塞产生的阻尼力较小，半主动阻尼拉杆表现出的阻尼力主要为运动活塞和缸筒的摩擦力，导致动刚度基本维持不变.10 Hz以后实测值与计算值基本一致.

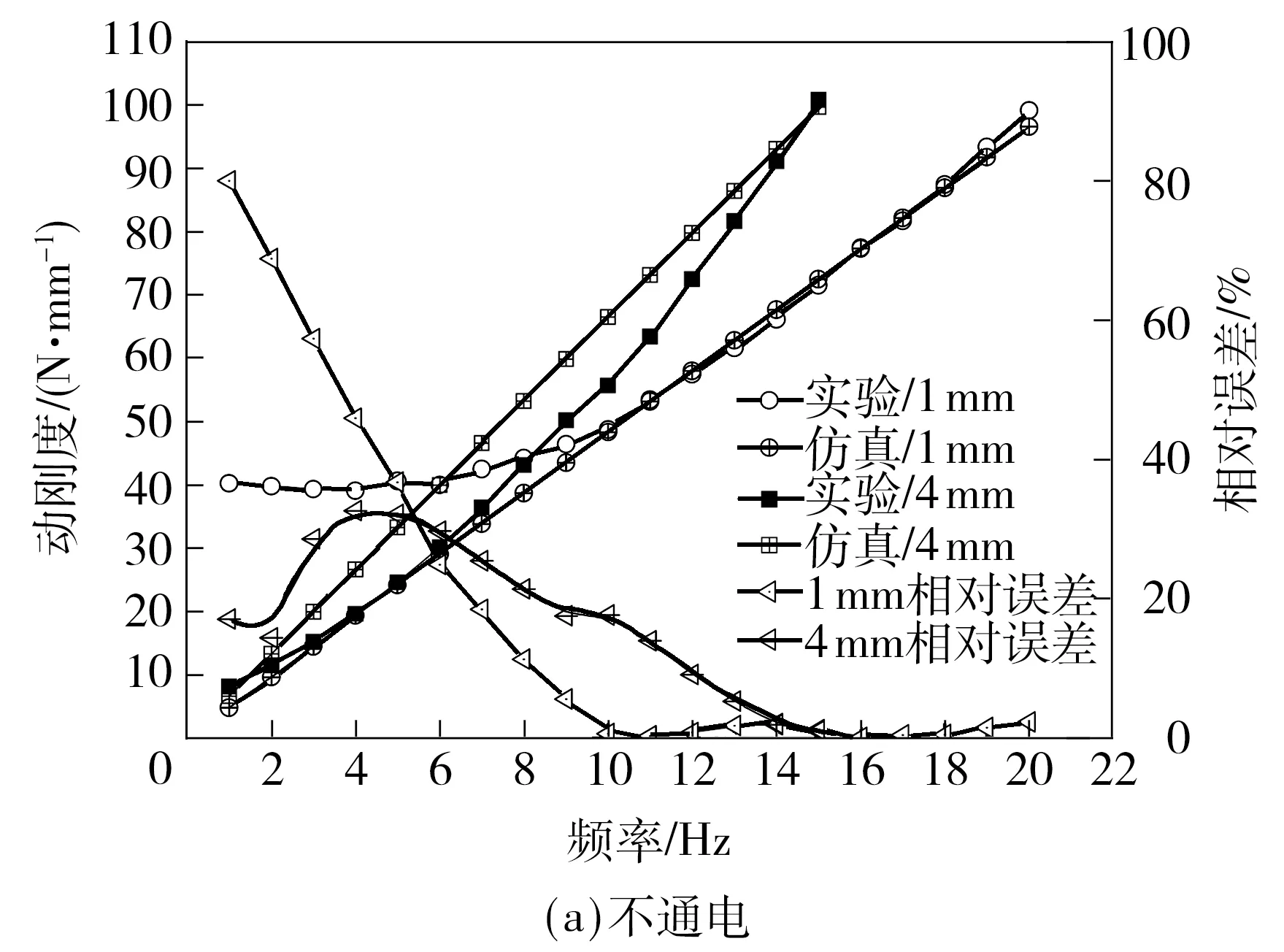
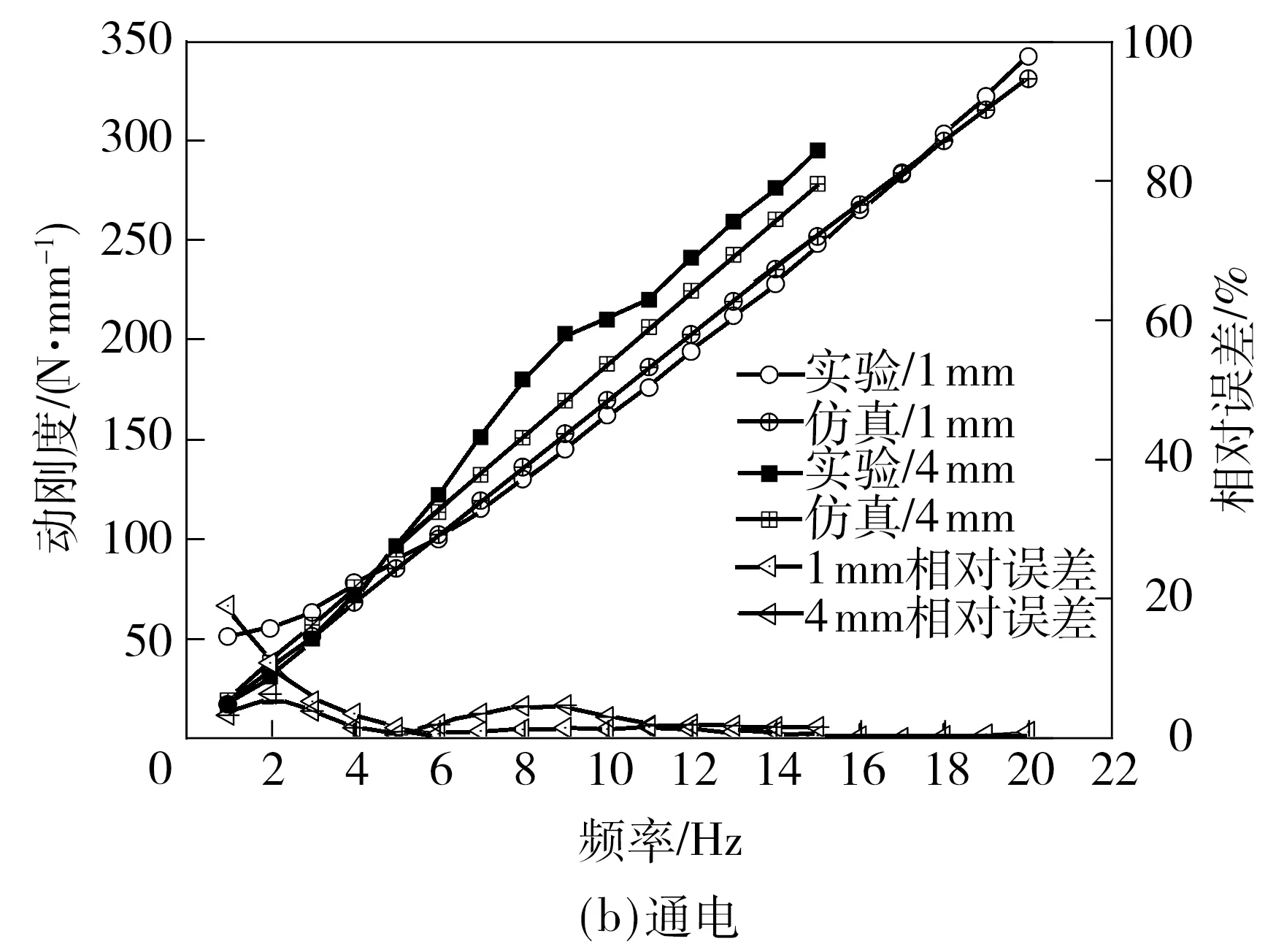
图10 动刚度的实验和计算对比Fig.10 Comparison of dynamic characteristics between experiment and simulation

4 动态性能分析

4.1 动刚度的影响因素分析

与液阻悬置类似，半主动阻尼拉杆的动刚度可以表示为存储动刚度和损失动刚度两个分量[15]，由第3节可知动刚度随频率变大逐渐变大.图11为振幅1 mm时存储刚度和损失刚度随频率变化的特性曲线，由图可知，低频阶段主要以损失刚度为主，损失刚度随频率先变大，在75 Hz时达到峰值后变小，其存储刚度随频率增加而逐渐增加.

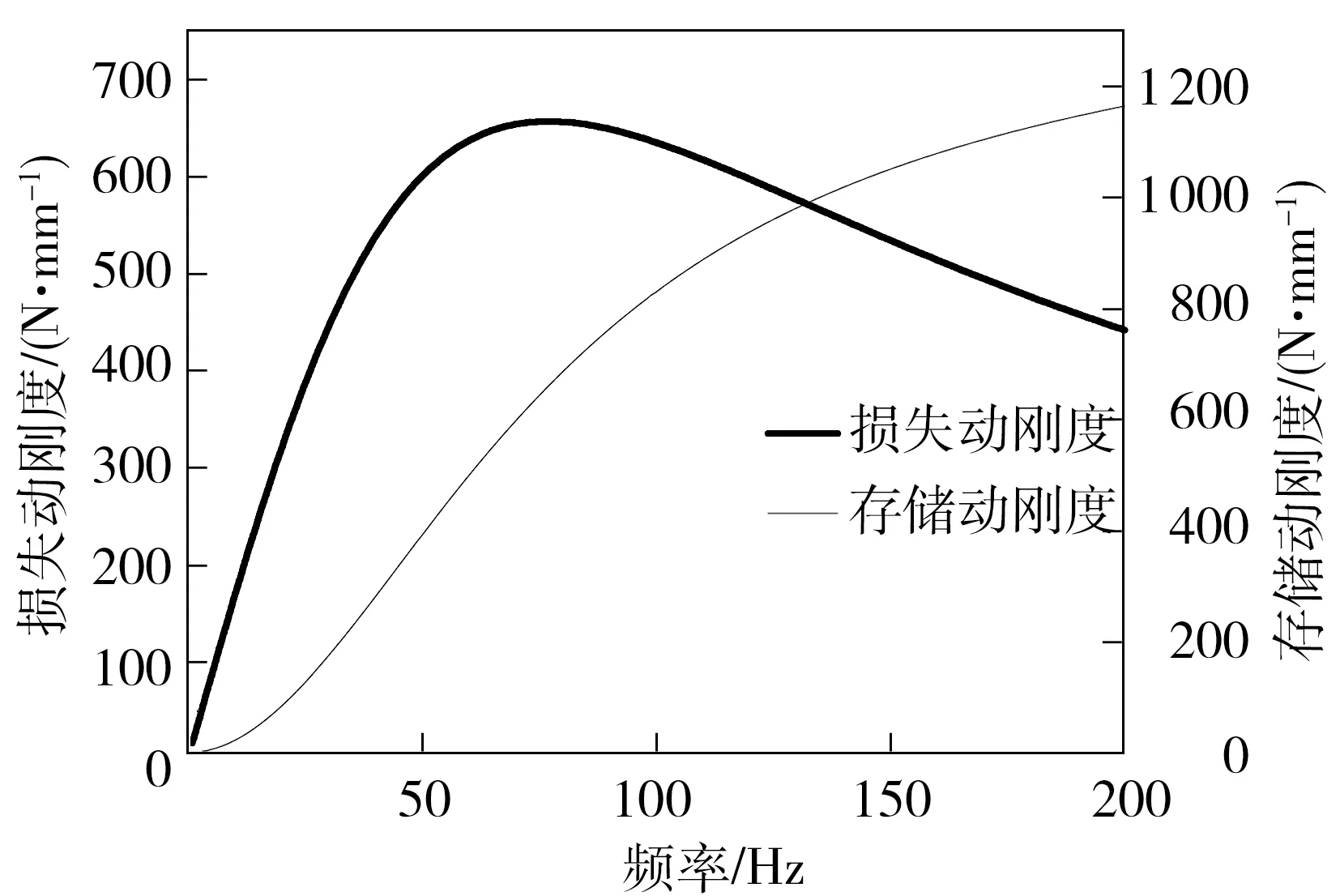
图11 半主动阻尼拉杆的动刚度特性Fig.11 Dynamic stiffness character of semi-acive damping strut

根据半主动阻尼拉杆动刚度的方程，可知半主动阻尼拉杆动刚度的主要影响因素为衬套刚度、阻尼常数及等效弹簧刚度.为分析各因素对动刚度的影响，采取如下措施：①通过不同橡胶配方，调整橡胶硬度，改变衬套刚度；②通过改变半主动阻尼拉杆运动活塞上的阻尼孔径和液压油黏度改变阻尼常数大小；③通过改变缸筒材料实现不同的等效弹簧刚度.图12为半主动阻尼拉杆的动刚度与衬套刚度、阻尼常数及等效弹簧刚度的关系.

由图12可知，等效弹簧刚度对半主动阻尼拉杆的动刚度的影响较衬套刚度和阻尼常数显著.由图12(a)-(c)可知，衬套胶料硬度越大(动刚度越大)，等效弹簧刚度和阻尼系数越大，半主动阻尼拉杆的动刚度也越大.在低频范围(1～10 Hz)时，衬套刚度和等效弹簧刚度对半主动阻尼拉杆动刚度的影响较小，半主动阻尼拉杆动刚度曲线基本重合.因此增加阻尼常数可以提高半主动阻尼拉杆低频时的动刚度，降低等效弹簧刚度和衬套刚度可以减小高频时的动刚度.

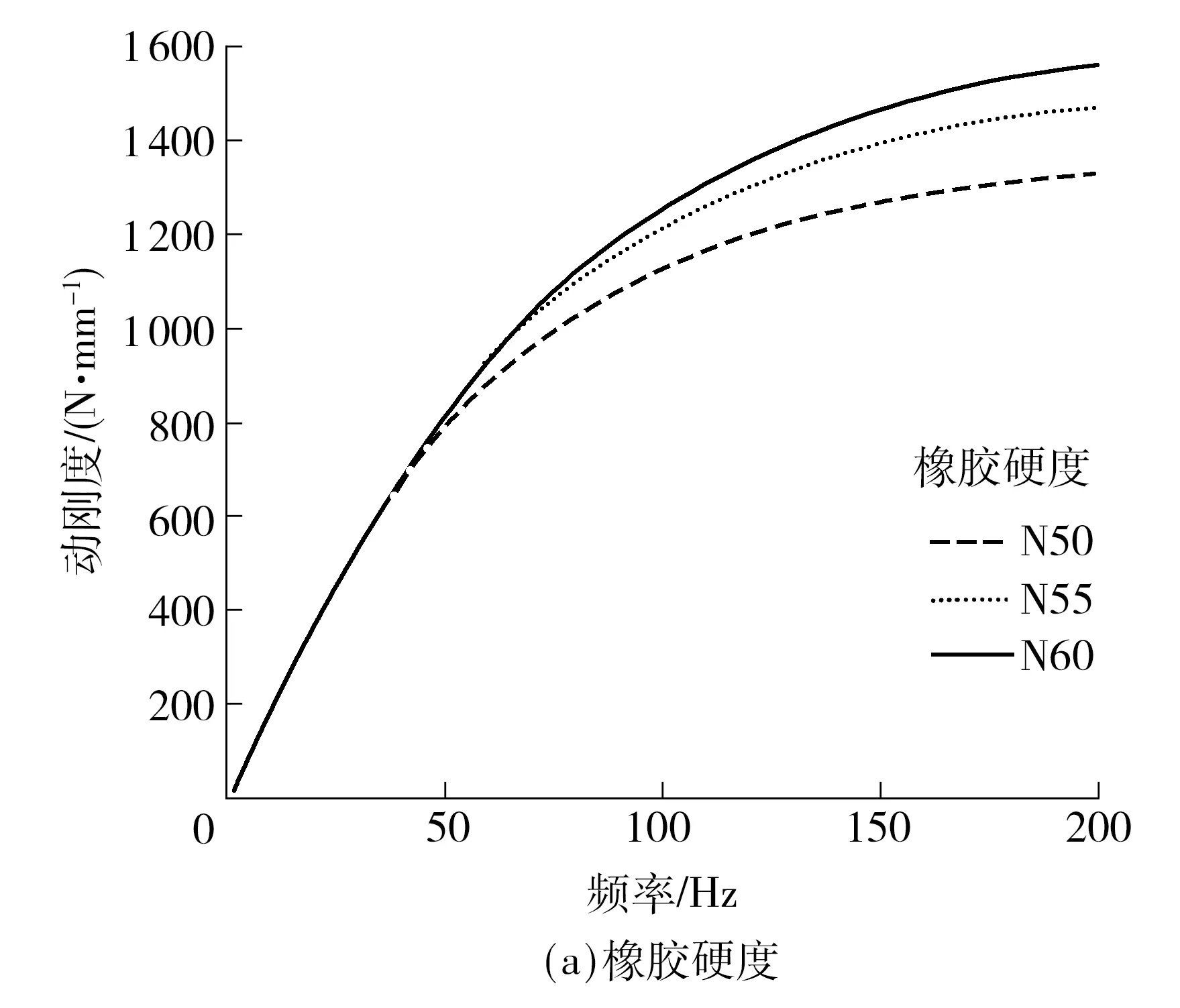
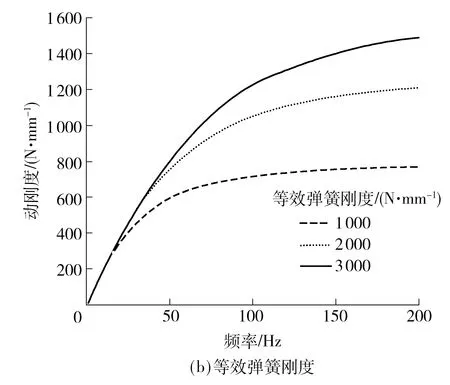
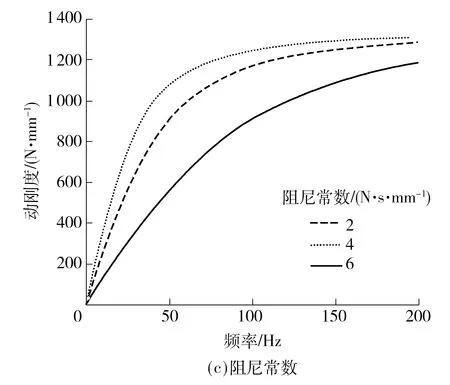
图12 动刚度的影响因素分析Fig.12 Influence factors analysis of dynamic stiffness

4.2 阻尼性能分析

由图11可知，在低频范围(1～50 Hz)内，半主动阻尼拉杆存储动刚度较小，主要以损失刚度为主，表现出较好的阻尼性能，此时有利于衰减发动机起停、原地换挡等瞬态工况下的冲击.在高频范围内，存储动刚度越来越大，为隔离高频振动，需要较小的阻尼.因此，为评价半主动阻尼拉杆在一定频率范围内的阻尼性能，采用阻尼分数即损失刚度与动刚度比值Md衡量.Md表示为

(20)

与动刚度的影响因素分析类似，图13为衬套刚度、阻尼常数和等效弹簧刚度与Md的关系.由图13可知，改变衬套刚度、等效弹簧刚度和阻尼常数时，Md随着频率增加呈减小趋势.由图13(a)知衬套刚度对半主动阻尼拉杆的阻尼性能的影响较小.由图13(b)可知，等效弹簧刚度越小，Md减小得越慢.由图13(c)可知，阻尼常数越小，Md减小得越慢.综上可知，减小等效弹簧刚度和阻尼常数能改善半主动阻尼拉杆低频时的隔振性能.增大阻尼常数有助于改善高频时的隔振性能.

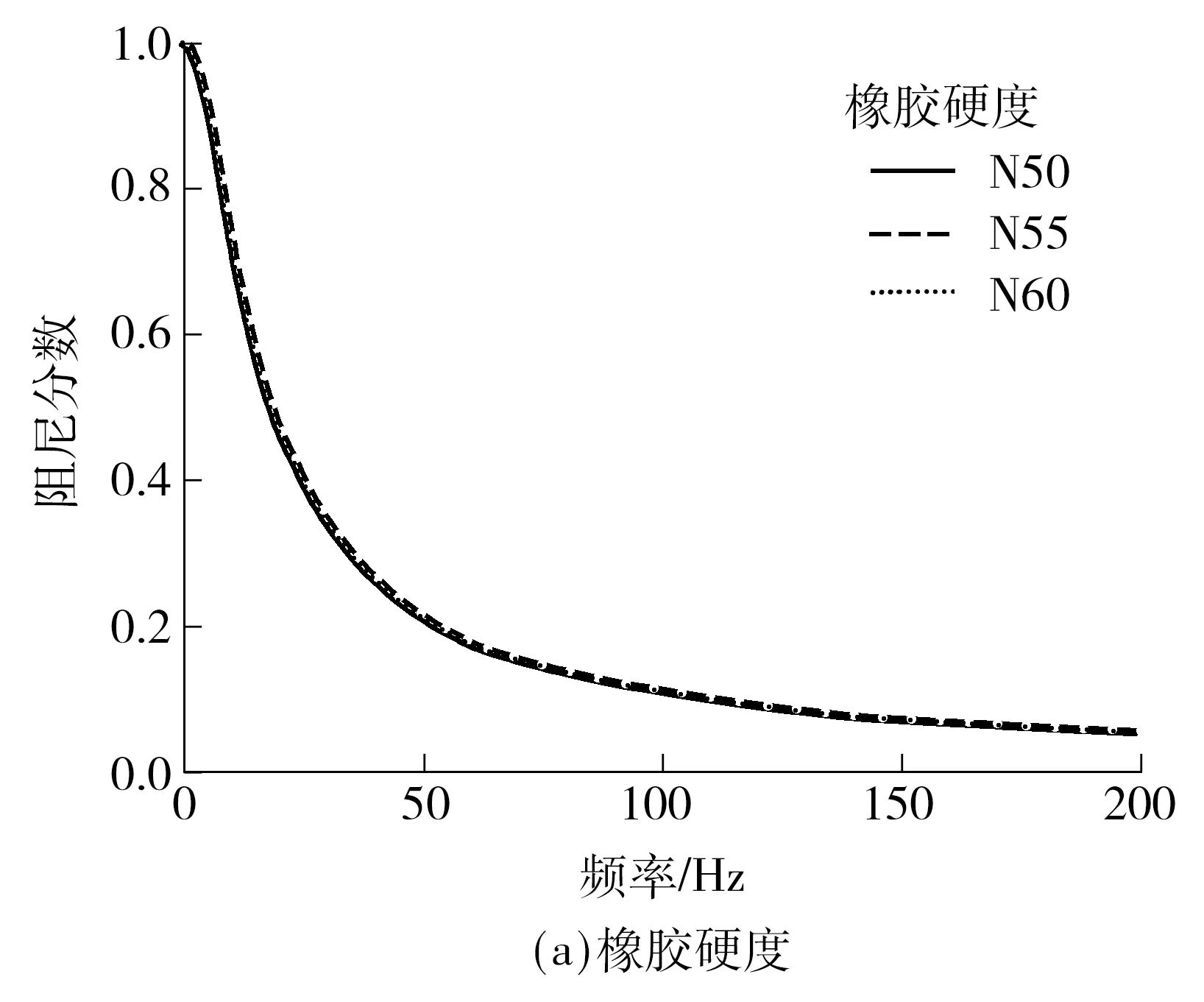
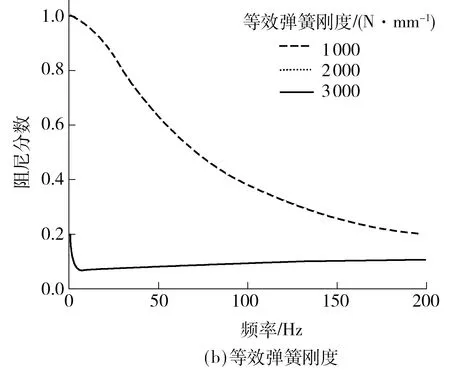
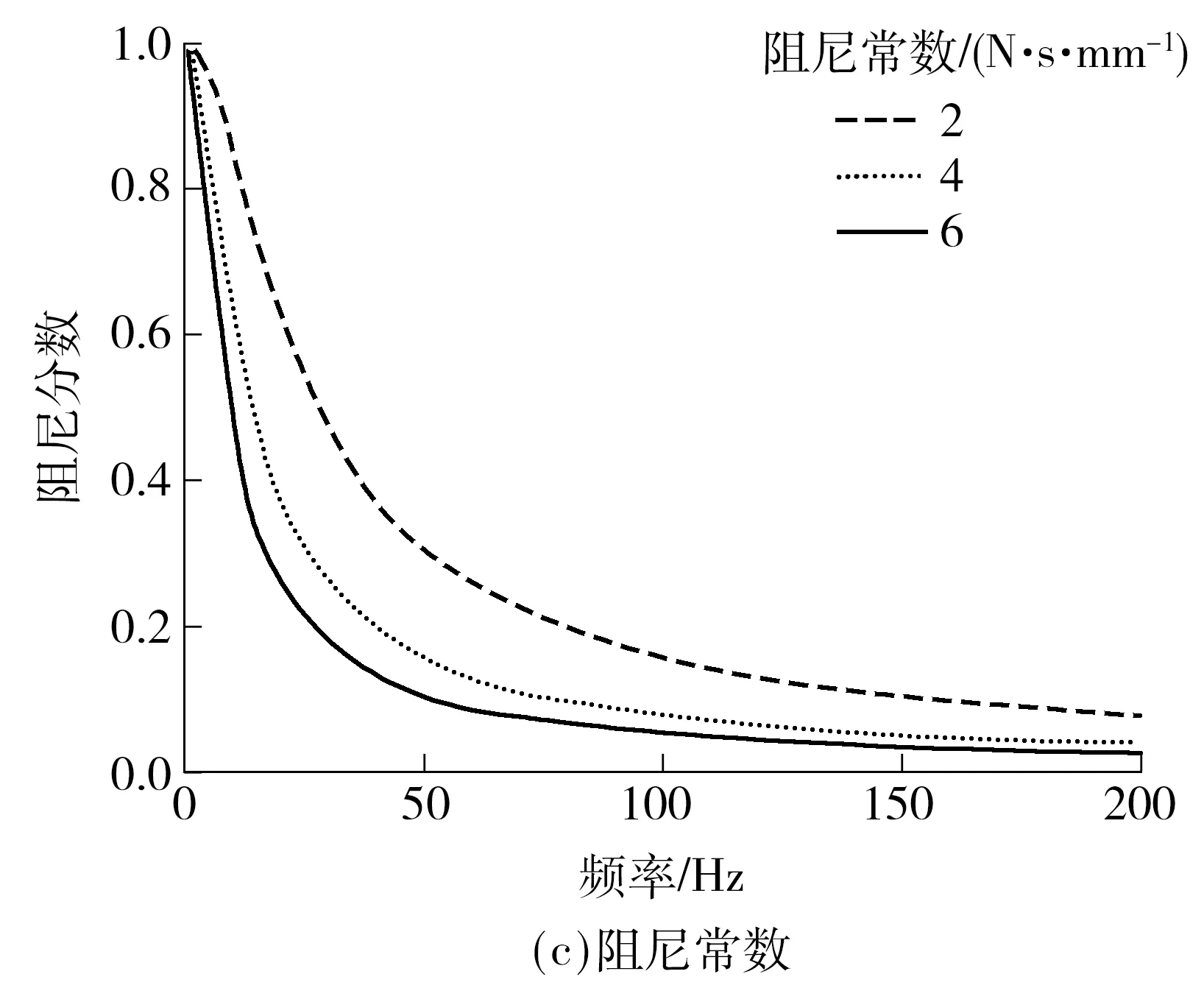
图13 阻尼分数的影响因素分析Fig.13 Influence factors analysis of damping fraction

5 结论

文中通过实验测试和仿真计算了通电和不通电情况下半主动阻尼拉杆在小振幅和大振幅下的动刚度值.通过对比发现：通电时，各个振幅下动刚度实验值和计算值吻合度较高；不通电时，大振幅下的吻合度良好.小振幅在低频段(1～10 Hz)存在一定的差异，主要是是由于运动位移小，通过运动活塞产生的阻尼力较小，半主动阻尼拉杆表现出的阻尼力主要为运动活塞和缸筒的摩擦力，导致动刚度基本维持不变.

文中还分析了衬套刚度、等效弹簧刚度和阻尼常数对半主动阻尼拉杆的动刚度和阻尼性能的影响，结果表明，当衬套刚度、等效弹簧刚度和阻尼常数较大时，半主动阻尼拉杆的动刚度较大.增加阻尼常数提高了半主动阻尼拉杆低频时的动刚度，降低等效弹簧刚度和衬套刚度可以减小高频时的动刚度.衬套刚度对阻尼性能影响较小.等效弹簧刚度和阻尼常数越小，半主动阻尼拉杆阻尼性能越好.

文中获得的半主动阻尼拉杆的动刚度模型适用于一般的液压减振器，对预测其动态性能有很好的指导作用.

[1] HE S,SINGH R.Approximate step response of a nonli-near hydraulic mount using a simplified linear model [J].Journal of Sound and Vibration,2007,229(3):656-663.

[2] 上官文斌，宋志顺，张云清，等.多惯性通道液阻悬置动态特性的实测与分析 [J].振动工程学报，2005,18(3):318-323.

SHANGGUAN Wen-bin,SONG Zhi-shun,ZHANG Yun-qing,et al.Experiment study and simulation analysis of hydraulic engine mounts with multiple inertia tracks [J].Journal of Vibration Engineering,2005,18(3):318-323.

[3] 上官文斌，吕振华.液阻型橡胶隔振器非线性特性仿真分析 [J].振动工程学报，2003,16(4):393-398.

SHANGGUAN Wen-bin,LU Zhen-hua.Nonlinear mode-ling and analysis of hydraulic damped rubber mounts [J].Journal of Vibration Engineering,2003,16(4):393-398.

[4] 杨超峰，殷志宏，吴川永，等.液压衬套与液阻悬置作用机理的对比分析 [J].华南理工大学学报(自然科学版),2015,43(8):82-90.

YANG Chao-feng,YIN Zhi-hong,WU Chuang-yong,et al.Comparison of working mechanisms of hydraulic damped bushings and hydraulic engine mount [J].Journal of South China University of Technology(Natural Science Edition),2015,43(8):82-90.

[5] KOWALSKI D,RAO M.Dynamic testing of shock absor-bers under non-sinusoidal conditions [J].Proceedings of the Institution of Mechanical Engineers Part D Journal of Automobile Engineering,2002,216(5):373-384.

[6] SONNENBURG R,STRETZ A.Dynamic properties of automotive damper modules [J].Archive of Applied Mechanics,2012,82(12):1795-1804.

[7] PRITZ T.Five-parameter fractional derivative model for polymeric damping materials [J].Journal of Sound and Vibration,2003,265(5):935-952.

[8] SCHMIDT A,GAUL L.Finite element formulation of viscoelastic constitutive equations using fractional time deri-vatives [J].Nonlinear Dynamics,2002,29(1/2/3/4):37-55.

[9] SJÖBERG M.Non-linear behavior of a rubber isolator system using fractional derivatives [J].Vehicle System Dynamics,2002,37(3):217-236.

[10] FRANCHER P,ERVIN R,MACADAM C,et al.Mea-surement and representation of the mechanical properties of truck leaf springs [C]∥West Coast International Meeting & Exposition.West Coast:[s.n.],1980.

[11] LEWANDOWSKI R,CHORAZYCZEWSKI B.Indentification of the parameters of the Kelvin-Voigt and the Maxwell fractional models,used to modeling of viscoelastic dampers [J].Computers and Structures,2010,88(1/2):1-17.

[12] WANG W,YU D,ZHOU Z.In-service parametric modeling a rail vehicle’s axle-box hydraulic damper for high-speed transit problems [J].Mechanical Systems and Signal Processing,2015,s 62/63:517-533.

[13] SONNENBURG R,STRETZ A.Damper modules with adapted stiffness ratio [J].Archive of Applied Mechanics,2011,81(7):853-862.

[14] KARI L.Extended fractional-order derivative viscoelastic material model for structure-borne sound analysis [M].[S.l.]:Trita-FKT,1997.

[15] SHANGGUAN Wen-bin.Engine mounts and powertrain mounting systems:a review [J].International Journal of Vehicle Design,2009,49(4):237-258.

s:Supported by the National Natural Science Foundation of China(51475171,11472107)

InvestigationintoDynamicCharacteristicsofSemi-ActiveHydraulicDampingStrut

WANGDao-yong1ZHAOXue-zhi1SHANGGUANWen-bin1,2YEBi-jun2

(1.School of Mechanical and Automotive Engineering,South China University of Technology,Guangzhou 510640, Guangdong,China;2.Ningbo Tuopu Group Co.,Ltd.,Ningbo 315800,Zhejiang,China)

In this paper,first,a semi-active hydraulic damping strut is made equivalent to a two-DOF model of mass and spring,and a dynamic stiffness expression is derived.Next,a nonlinear rubber bushing model based on the linear elasticity,the fractional derivative and the friction model,is constructed,and the Maxwell model is adopted to describe the stiffness of a general damper.Then,the parameters in the dynamic stiffness model of the rubber bushing and the general damper are identified by means of the least square method.Finally,the dynamic stiffness of the semi-active hydraulic damping strut under power-on conditions is compared with that under power-off condition through experiments and simulations,and the influence of the equivalent spring stiffness,the damping constant and the rubber bushing stiffness on the dynamic stiffness and damping capacity of the semi-active hydraulic damping strut is analyzed.The results show that (1) the dynamic stiffness of the semi-active hydraulic damping strut increases with the increase of the rubber bushing stiffness,the equivalent spring stiffness and the damping constant;(2) increasing the damping constant helps to improve the dynamic stiffness of the semi-active hydraulic damping strut at low frequencies,and decreasing the rubber bushing stiffness and the equivalent spring stiffness helps to reduce the dynamic stiffness of the semi-active hydraulic damping strut at high frequencies;(3) the ru-bber bushing stiffness has a smaller effect on the damping capacity of the semi-active hydraulic damping strut;and (4) the smaller the equivalent spring stiffness and the damping constant are,the better the damping capacity of the semi-active hydraulic damping strut will be.

semi-active hydraulic damping strut;dynamic stiffness;damping capacity

2016-12-01

国家自然科学基金资助项目(51475171,11472107)

王道勇(1987-)，男，博士生，主要从事汽车动力总成振动与噪声控制、液阻橡胶隔振器及液压减震器研究.E-mail:806296192@qq.com

†通信作者:上官文斌(1963-)，男，博士，教授，博士生导师，主要从事汽车振动、噪声分析与控制、汽车悬架与转向系统的设计与分析、发动机热管理系统设计与开发、汽车设计理论与方法研究.E-mail:sgwb@163.com

1000-565X(2017)08-0013-08

TH 113;U 464

10.3969/j.issn.1000-565X.2017.08.003