变速工况下某变速器壳体的动态响应分析*

臧孟炎 孟宁 褚淑敏 陈勇

(1.华南理工大学 机械与汽车工程学院，广东 广州 510640；2.浙江吉利汽车研究院有限公司，浙江 杭州 311228；3.河北工业大学 机械工程学院，天津 300130)

变速工况下某变速器壳体的动态响应分析*

臧孟炎1孟宁1褚淑敏2陈勇3

(1.华南理工大学 机械与汽车工程学院，广东 广州 510640；2.浙江吉利汽车研究院有限公司，浙江 杭州 311228；3.河北工业大学 机械工程学院，天津 300130)

基于多体系统动力学理论，综合考虑齿轮副时变啮合刚度、齿侧间隙、轴承刚度及阻尼、转速连续变化的影响，建立了变速器传动系统动力学模型，计算得到齿轮动态啮合力和壳体各轴承座处的动态支反力.然后对变速器壳体柔性化处理，获得变速器壳体固有频率及振型.最后以各轴承座处的动态支反力为激励，采用模态叠加法计算壳体结构的动态响应，获得了壳体表面的振动信息.仿真结果表明：在扭矩一定时，变速器壳体表面振动加速度幅值随转速升高呈增大趋势，与实验台架实测结果吻合良好，并且误差在10%以内.

变速器；动力学分析；模态叠加法；动态响应

齿轮传动装置是动力总成的重要组成部分，具有结构紧凑、效率高、传动比稳定等优点，被广泛应用于车辆、船舶、工程机械等领域.在传动过程中，由于齿轮啮合时变刚度和轴承动态载荷的变化，使得变速器壳体产生振动.若激励频率与变速器壳体的某阶固有频率相同或接近，会使壳体产生共振，并导致在壳体某些部位产生很大的振动幅值，进而影响整车的NVH(振动、噪声、声噪粗糙度)性能.随着人们对乘车驾驶的舒适性要求越来越高，对变速器壳体动态特性及振动水平的准确预估显得尤为重要.Iwatsubo等[1]建立了齿轮传动系统的弯扭耦合动力学模型，考虑了系统的轮齿时变啮合刚度和综合啮合误差对系统振动的影响.Sellgren等[2]采用有限元法分析了齿轮箱动态响应，研究了模型中不同的轴承连接形式及其刚度对动响应的影响，并分析了齿轮啮合状态、箱体结构刚度及工况条件对齿轮箱振动的影响.王立华等[3]建立了斜齿轮副的弯曲-扭转-轴向-扭摆耦合振动的动力学模型，求解了齿轮系统的振动响应.Parker等[4-5]利用有限元及接触力学模型分析了具有时变刚度和齿侧间隙的齿轮副动态响应及齿轮接触冲击、齿间载荷分布以及齿廓修型等.杨振等[6]考虑齿侧间隙和内外激励等因素的作用，建立齿轮系统多自由度耦合动力学模型，并对系统的振动特性进行分析.朱才朝等[7]建立了考虑传动子系统内部激励和外部激励的船用齿轮箱系统有限元模型，计算了系统的动态响应，并对系统动态响应进行了数值特性分析.林腾蛟等[8-10]通过三维接触有限元法分析得出齿轮啮合动态激励是齿轮系统产生振动和噪声的基本原因.王炎等[11]建立了齿轮系统刚柔耦合动力学模型并仿真得出了箱体节点振动加速度信号.刘辉等[12]建立了变速箱刚柔耦合多体动力学仿真分析模型，得到了箱体各轴承座处的动态力，并利用模态叠加法对箱体结构进行了动态响应求解.贺朝霞等[13]建立了一个时变的、多自由度耦合行星齿轮传动系统动力学模型，并求解系统动态响应.以上文献通过对齿轮箱系统的振动特性分析，得出了大量有价值的研究成果，但没有考虑变速情况下的齿轮箱振动响应变化.对于需要不断升降速的变速器传动系统来说，正确估算齿轮动态啮合力和壳体动态响应对变速器设计有着重要意义.

文中以某款变速器齿轮箱为研究对象，综合考虑齿轮副的时变啮合刚度、齿侧间隙、轴承支撑刚度的影响，利用多体动力学仿真分析方法计算得到变速箱轴承座处的动态支反力.在此基础上采用模态叠加法计算柔性壳体结构的动态响应，获得壳体表面各节点的振动信息，并与实验结果进行对比分析.

1 动态响应分析理论

振动响应的分析方法主要有直接积分法和模态叠加法，文中选用模态叠加法求解变速器齿轮箱系统动态响应[14].考虑粘性阻尼的多自由度系统强迫振动方程为

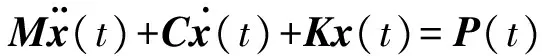
(1)

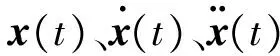
以正则振型矩阵Ψ作为变换矩阵，作如下变换：

x(t)=Ψξ(t)

(2)

(3)

式中，ΨTMΨ、ΨTCΨ、ΨTKΨ分别为模态质量、阻尼和刚度矩阵，ΨTP(t)为模态力向量.这时方程已全部解耦，利用Duhamel积分求得解耦后系统第i阶模态对应的模态坐标的响应为

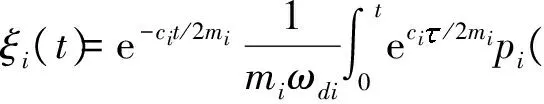
(4)

式中,ωdi为有阻尼固有频率,ci、mi、pi分别为C、M、P元素.

求得每阶振型的响应后，根据式(2)进行线性叠加，从而得到系统振动响应，即

(5)

2 变速器传动装置的多体动力学仿真

2.1 多体动力学分析模型

在Pro/E中根据各零件的实际参数建立变速器的三维实体模型，定义材料及装配关系后导入到LMS Virtual Lab软件的Motion模块中，如图1所示，然后根据变速器模型各零部件的实际运动关系建立对应的运动副.基于Cai理论[15]的轮齿刚度计算方法，在相互啮合的齿轮对间设置齿轮接触力，定义齿轮的几何参数(齿宽、齿数、变位系数、模数、螺旋角、压力角)和接触参数(齿侧间隙、时变刚度、啮合阻尼、轴向及端面重合度).表1给出了分析模型的主要参数.在轴承座处采用衬套力将轴承衬套化，并定义轴承的刚度和阻尼.在输入轴处添加旋转副，施加转速驱动，对于升降速工况还需添加扫频记录速度变化.输出半轴左右两端添加扭簧单元(RSDA)，施加负载扭矩.

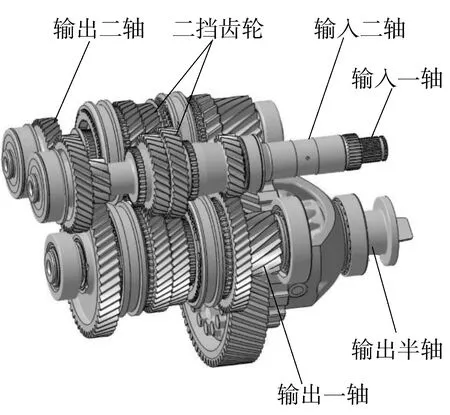
图1 变速器齿轮传动系模型Fig.1 Model of the gear transmission system

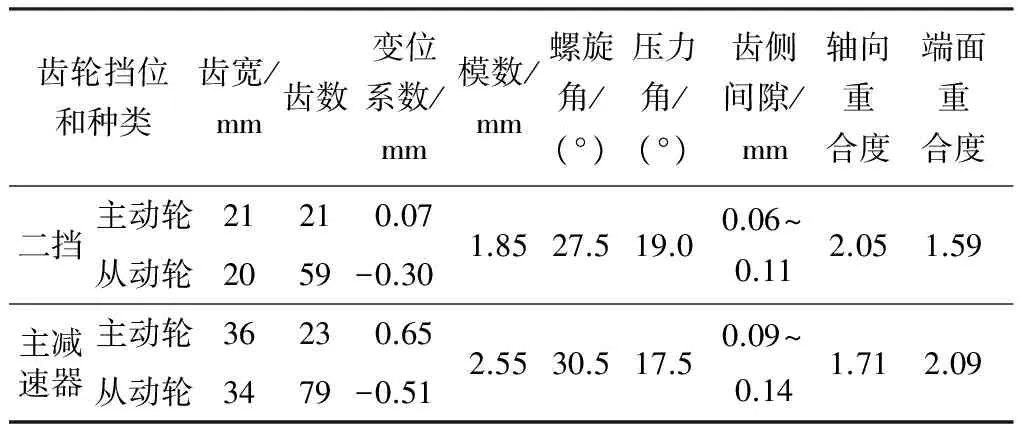
表1 齿轮分析模型的基本参数Table 1 Basic parameters of gear analysis model

2.2 齿轮系统动力学求解

综合考虑齿轮时变刚度、啮合阻尼、齿侧间隙、轴承支撑刚度与阻尼的影响，将建立的齿轮传动装置多体动力学模型进行仿真求解.文中以该变速器二挡工况为例，分析升、降速过程的振动响应，即升速工况输入转速由1 500 r/min阶梯升至5 000 r/min，降速工况输入转速由5 000 r/min阶梯降至1 500 r/min.转速阶梯升降间隔为50 r/min.

已知输入扭矩为83 N·m，由二挡总速比为9.65可知，在输出半轴左右两端各添加400.48 N·m负载扭矩，仿真计算得到二挡齿轮动态啮合力及8个轴承座处各个方向的支反力.图2、3分别给出了二挡升速过程主动齿轮的轴向动态啮合力、输入二轴前轴承座轴向支反力和输入转速的关系.

由图2和3可知，在轴线方向，齿轮啮合力均值和输入二轴前轴承支反力均值相等，力的变化幅值均随着转速的增加而增加.在3 900 r/min左右，变速器传动系发生共振现象，齿轮啮合力幅值和轴承支反力幅值急剧增大，随着转速进一步提高，共振现象消失.

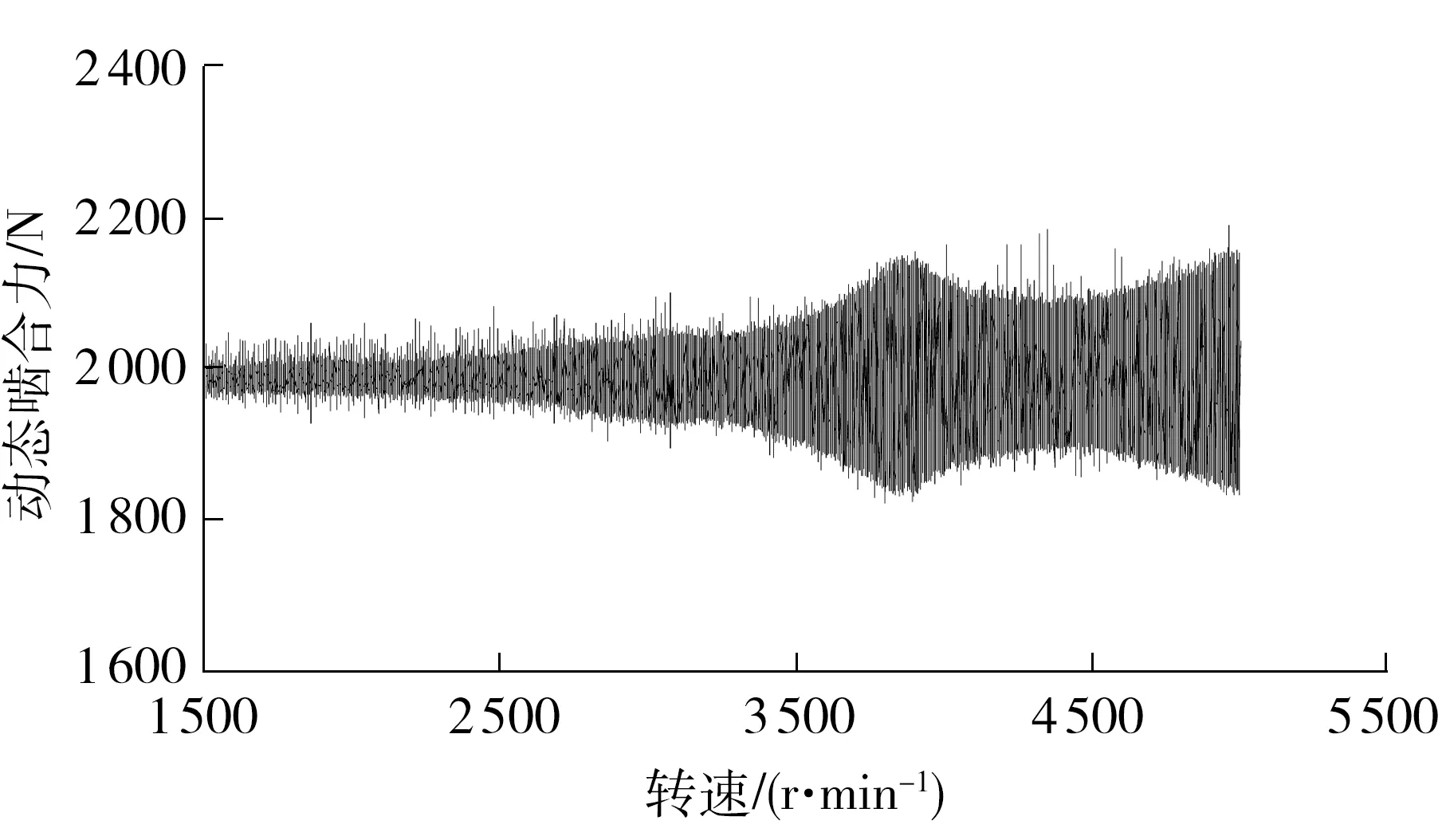
图2 二挡主动齿轮轴向动态啮合力Fig.2 Axial dynamic meshing force of the second driving gear

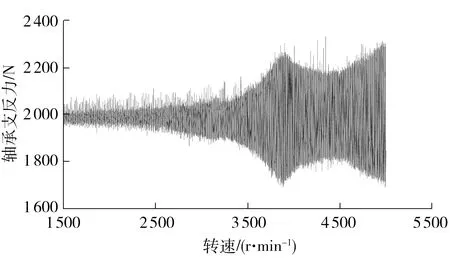
图3 输入二轴前轴承轴向支反力Fig.3 Axial reaction force of the front bearing at the second input shaft

3 变速器壳体动态响应分析

3.1 壳体有限元模型的建立

将变速器壳体导入Hypermesh进行几何清理并划分网格.定义壳体材料密度ρ=2.7×103kg/m3、杨氏模量E=70 GPa和泊松比μ=0.34.模型共划分节点178 087个，四面体单元629 902个.变速器前后壳体间的螺栓连接和变速器前壳体端面与台架的螺栓连接通过定义rbe2单元实现约束.

将壳体网格文件导入到LMS Virtual Lab软件中，在轴承座处定义刚性单元后，软件将自动捕捉并建立联接点，轴承座处动态支反力通过该点传给变速器壳体.变速器壳体有限元模型如图4所示，图中标注了壳体表面3个动态响应测点位置，分别为输出一轴轴承座处、输入轴和输出二轴轴承座交汇处以及差速器轴承座处.

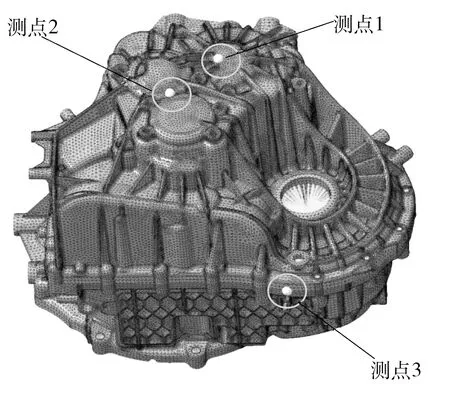
图4 变速器壳体有限元网格Fig.4 Finite element meshes of the transmission housing

3.2 壳体模态分析

在柔性体分析模块中，采用Lanczos法对变速器壳体进行模态分析，设置模态频率求解范围为0～10 000 Hz，共有167阶模态.表2给出了前15阶固有频率，图5为壳体前4阶模态振型.

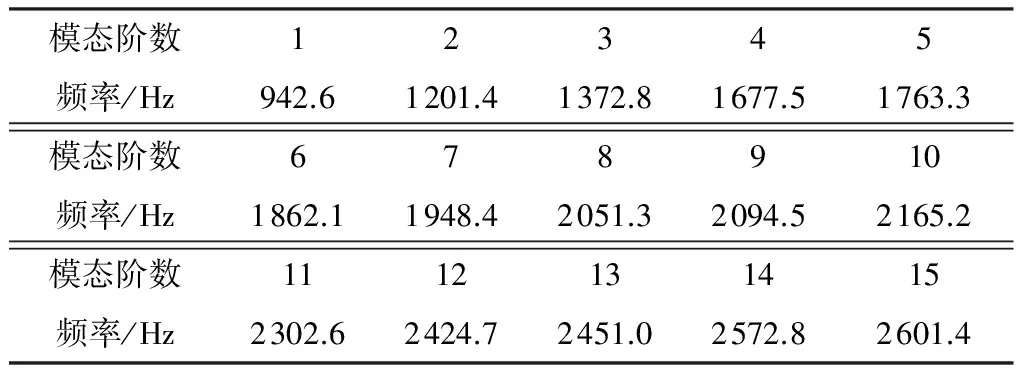
表2 壳体前15阶固有频率Table 2 Natural frequency of first 15 orders of the housing

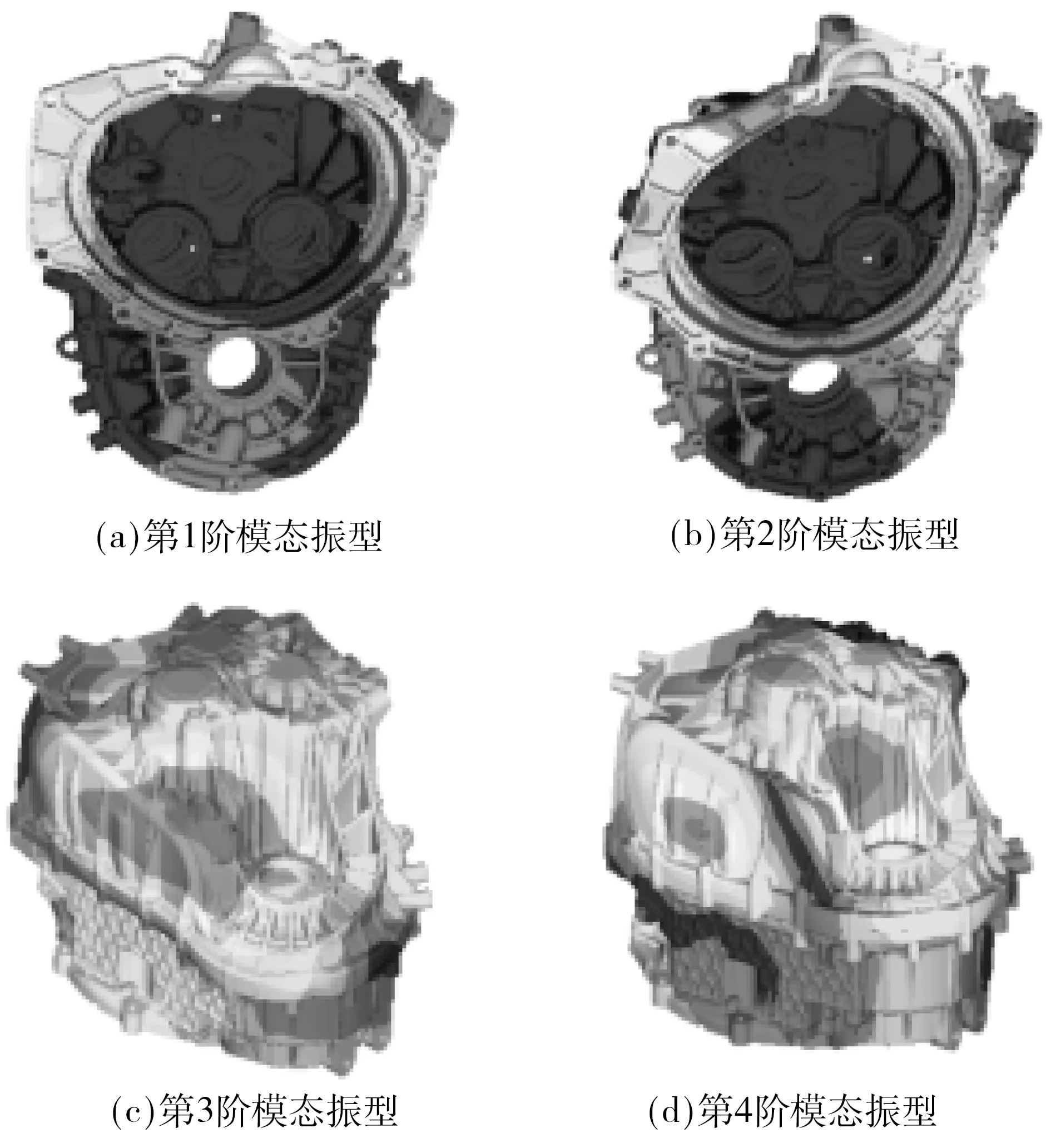
图5 变速器壳体前4阶模态振型Fig.5 Modal shapes of first 4 orders of the transmission housing

3.3 变速器壳体动态响应分析

将上述多体动力学仿真求得的8个轴承座处的动态支反力作为激励，在LMS Virtual Lab中采用模态叠加法计算变速器壳体动态响应.图6和7分别为测点1的轴向动态响应的时域曲线和频谱图(考虑到论文篇幅，测点2和3的相关结果未列出).

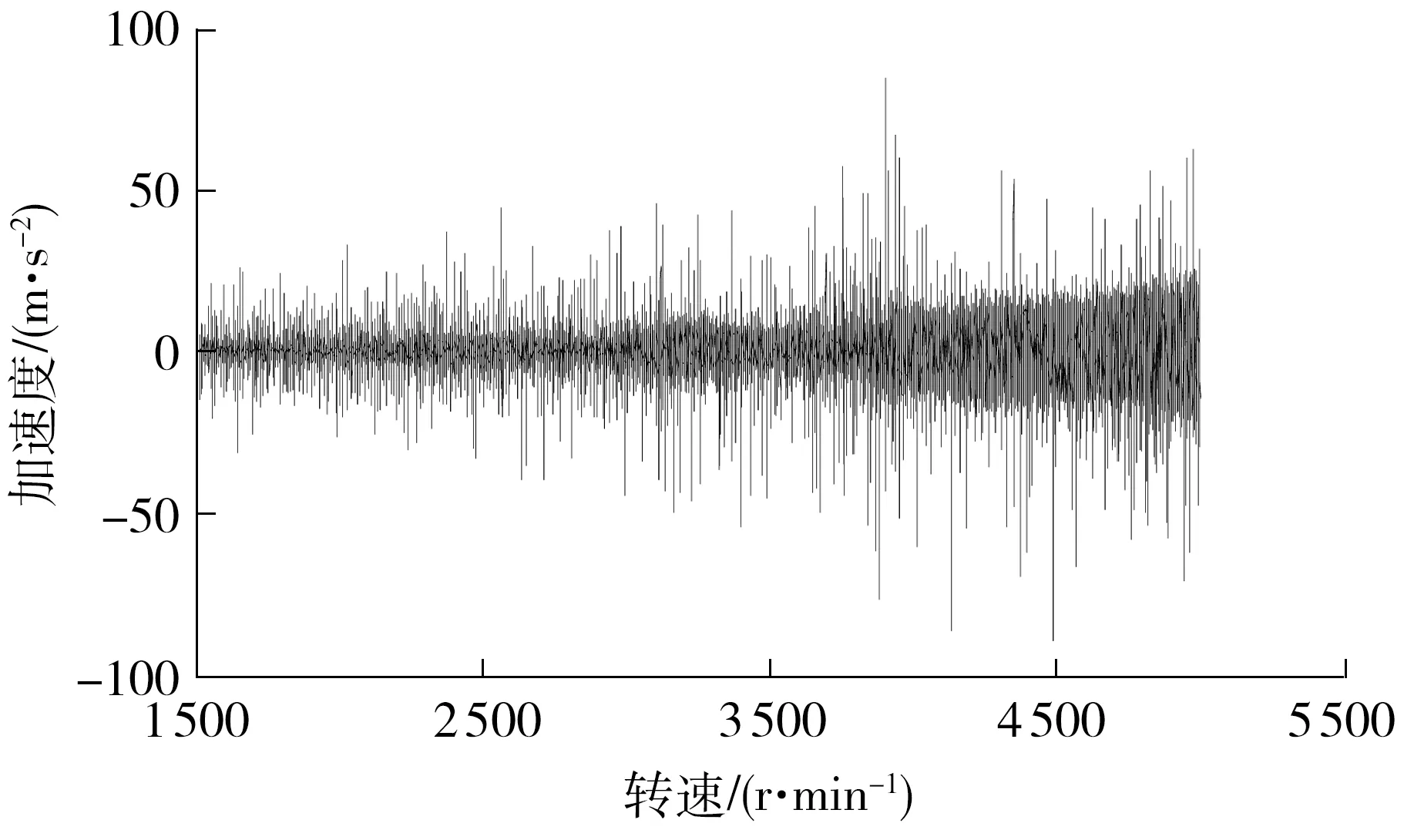
图6 测点1轴向振动加速度曲线Fig.6 Axial vibration acceleration curve at test point 1

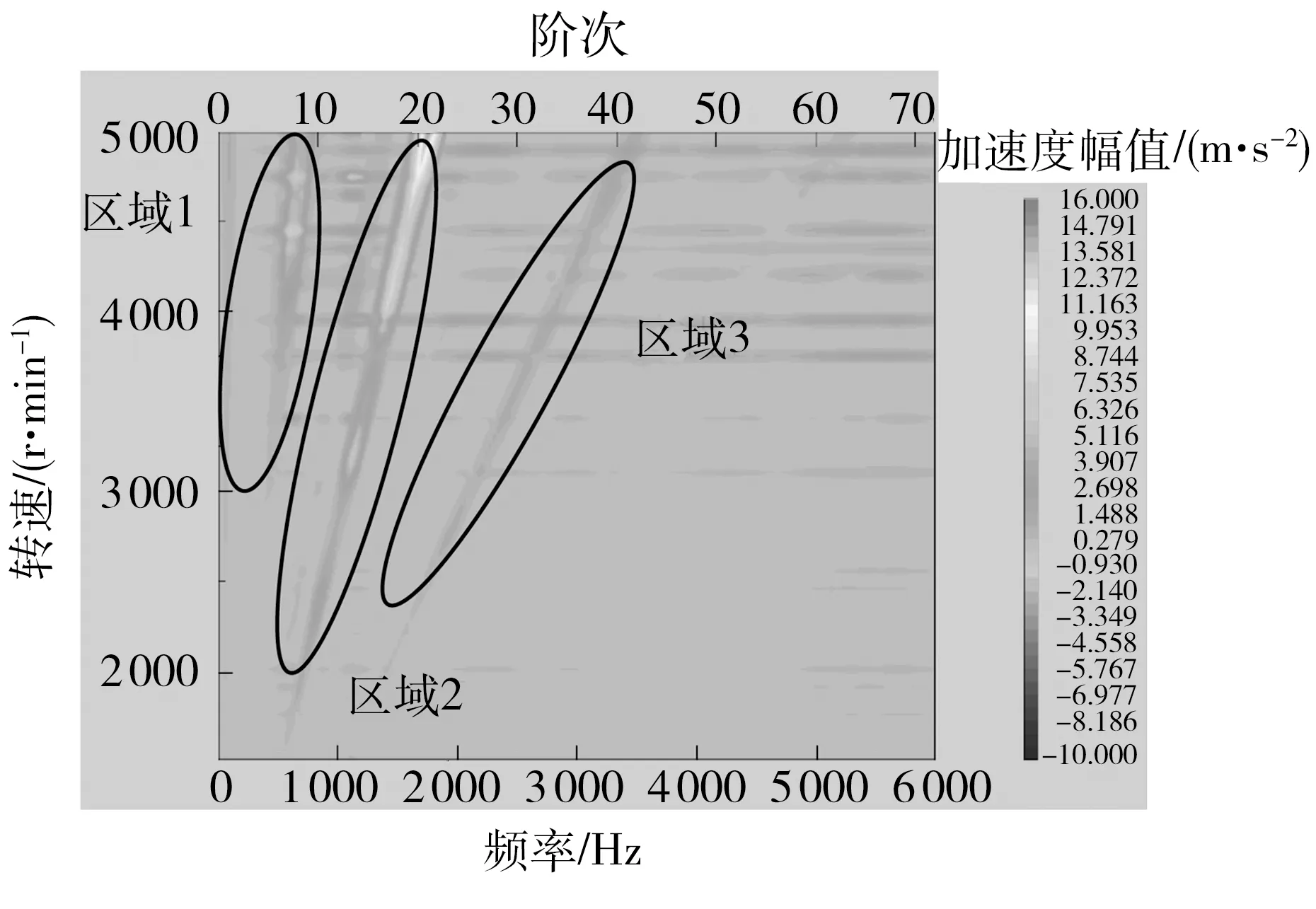
图7 测点1振动加速度频谱图Fig.7 Vibration acceleration spectrum at test point 1

由图6可以看出，随着输入转速的升高，加速度振动幅值逐渐变大，在3 900 r/min时，振动加速度幅值有明显峰值，变速器发生共振现象.由于变速器升降速时壳体表面的振动情况属于非平稳振动信号，齿轮啮合频率随转速变化而变化，通常使用阶次来描述啮合频率在变转速下的特征.图7所示的频谱图中，上横坐标为阶次，下横坐标为频率，纵坐标为转速，云图颜色的深浅代表加速度幅值的大小，区域1、2、3分别对应主减速器齿轮啮合阶次(8.19阶)、二挡齿轮啮合阶次(21阶)及其2阶谐波(42阶).这些承载齿轮啮合阶次及其谐波主要影响变速器齿轮啸叫，随着转速的上升，齿轮啸叫能量增大，造成变速器壳体振动加剧.

4 仿真结果评价

为验证仿真结果的准确性，实施了相应台架实验，并将二挡齿轮啮合阶次(21阶)的振动加速度与实验进行对比.

使用加速度传感器将测得的振动加速度信号由信号采集处理分析仪采集，再用Artemis SUITE分析软件进行数据处理，得到壳体表面3个测试点第21阶的振动加速度幅值，并将其转化为振动加速度级.图8和9分别为各测点升速和降速工况下的仿真计算与实验结果曲线.

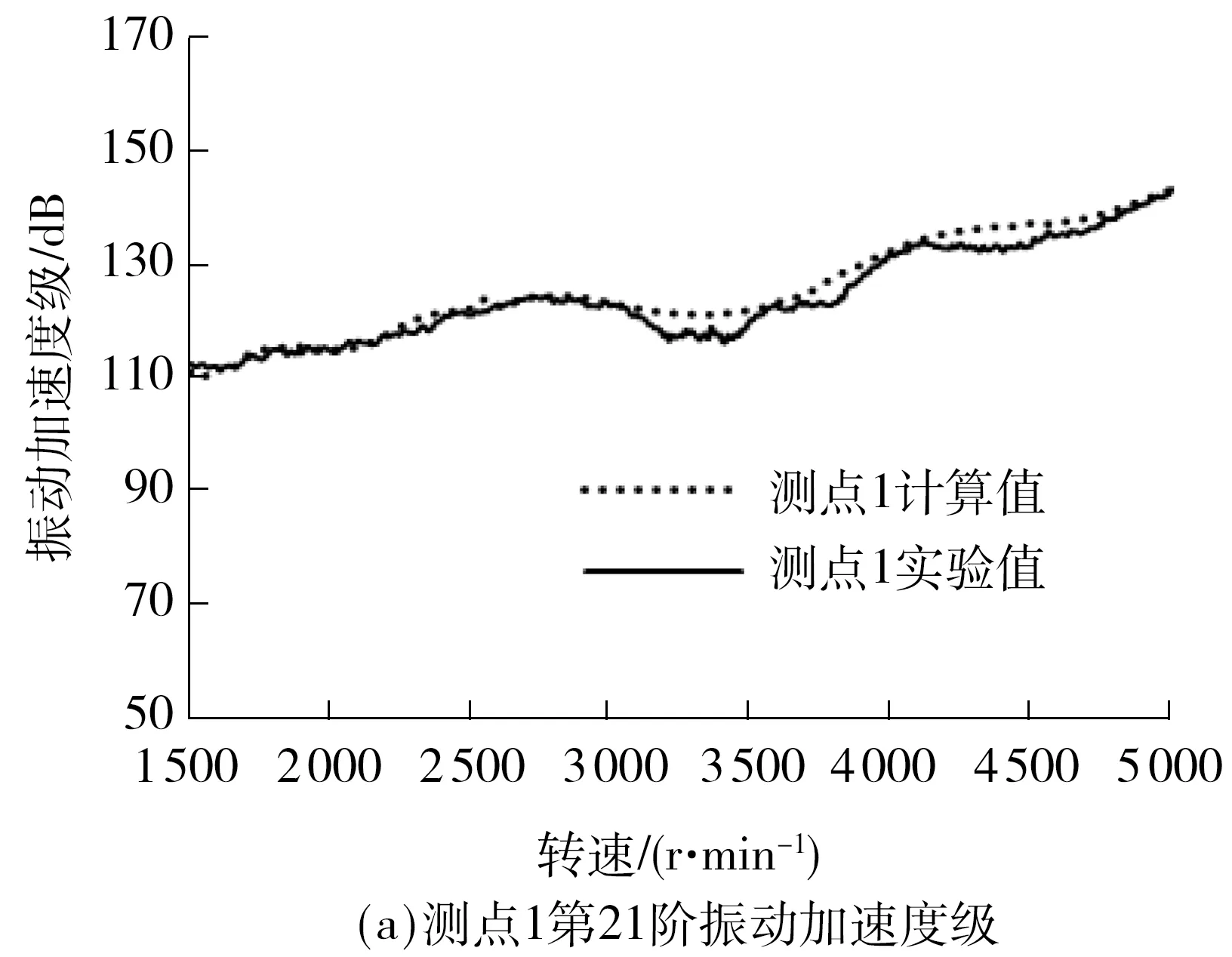
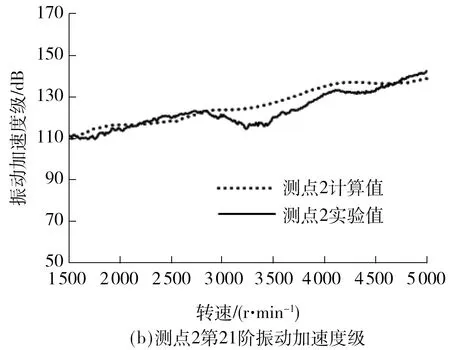
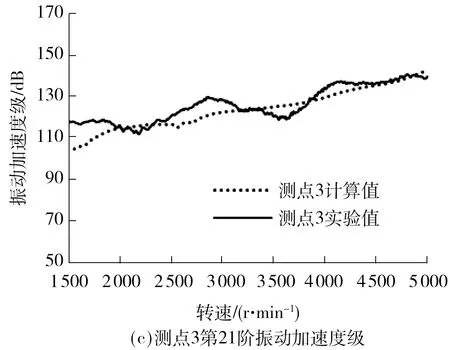
图8 升速工况下各测点的振动加速度级Fig.8 Acceleration structure noise at each test point under the conditions of speed up

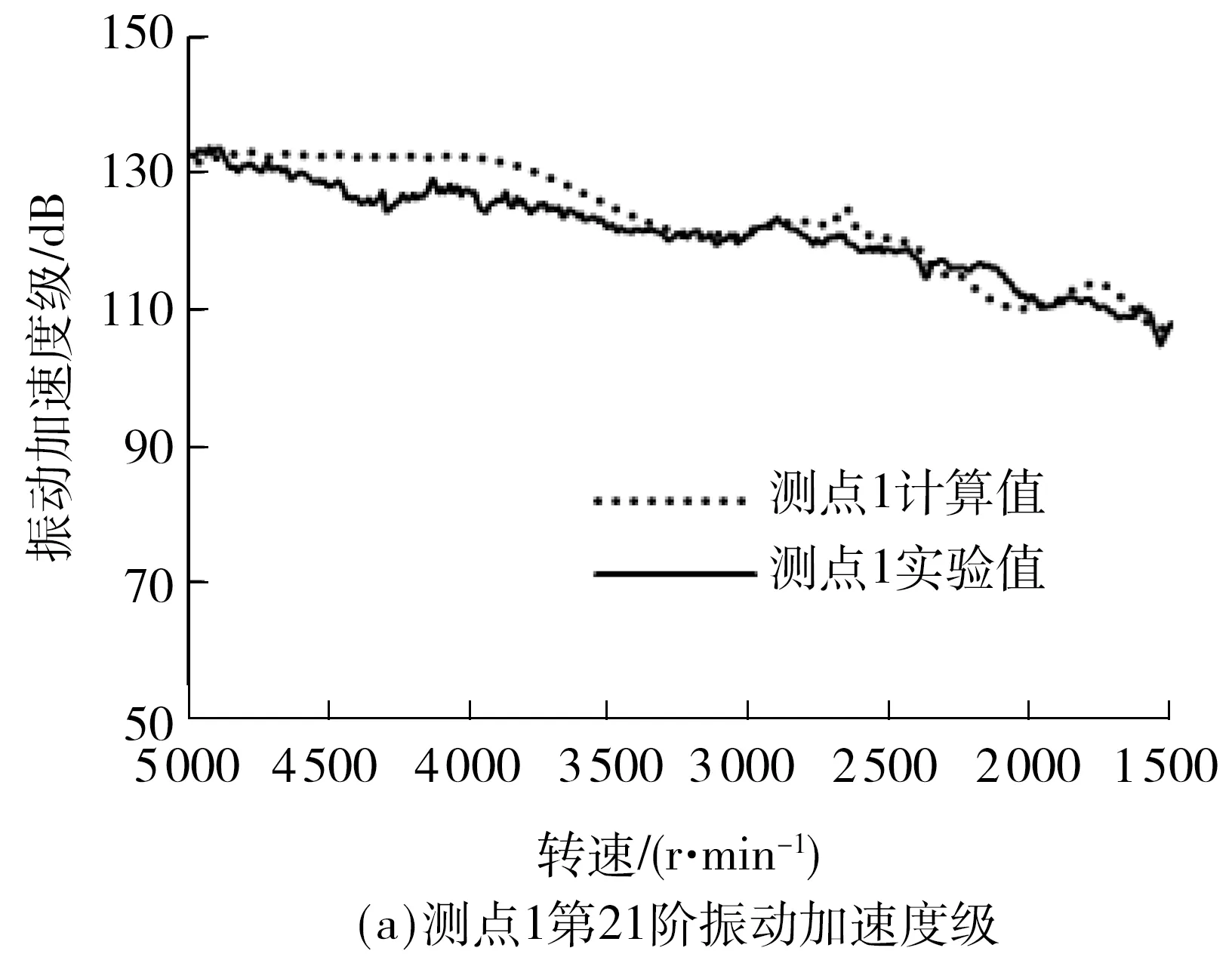
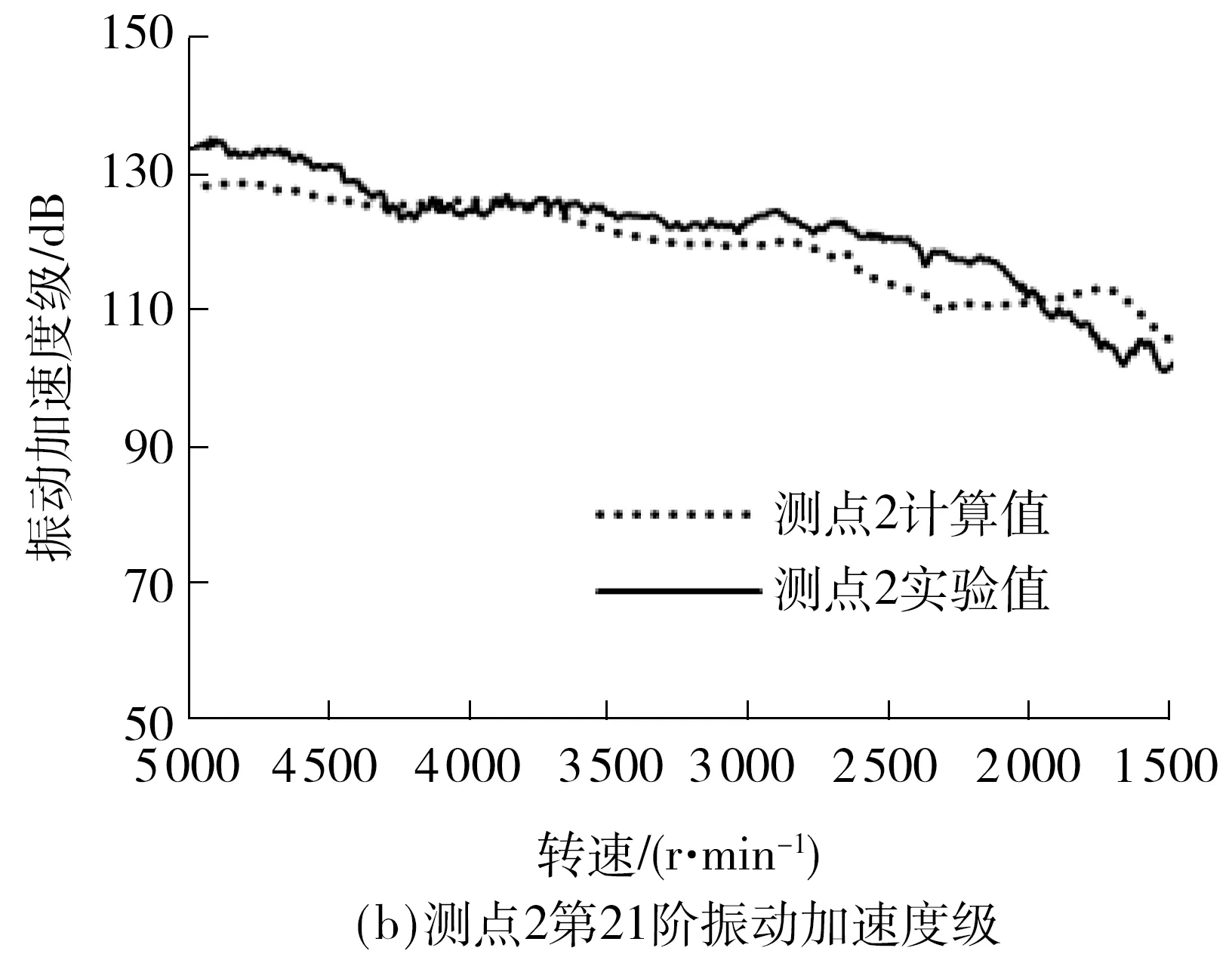
图9 降速工况下各测点振动加速度级Fig.9 Acceleration structure noise at each test point under the conditions of speed down

变速器输入转速由1 500 r/min升至5 000 r/min时，壳体表面3个测点仿真与实验的振动加速度级总体呈上升趋势，而降速时噪声值呈下降趋势.这是由于升速时，变速器内部齿轮敲击与啸叫能量增大，导致壳体表面振动加速度级的数值增大.降速时能量减小，敲击和啸叫减弱，振动加速度级数值随之减小.

对比二挡升速工况壳体表面振动加速可以看出，降速工况时壳体振动较小，主要是因为变速器反拖降速时的扭矩较小，能量较低，因此振动也较小.由图8和9可知，仿真与实验结果较为吻合，说明所建模型能够合理反映变速器真实振动状态.

5 结论

文中建立了变速器壳体与传动系统的刚柔耦合动力学模型，并综合考虑了齿轮时变刚度、轴承支撑刚度的影响，计算得到了齿轮动态啮合力及轴承座处的动态激励.对变速器壳体进行模态分析，利用模态叠加法计算了壳体的动态响应.壳体表面振动加速度随着转速增加而呈增大趋势，与变速器台架实验结果基本一致.研究方法对变速器壳体设计优化具有指导意义.

[1] IWATUSBO N,ARII S,KAWAI R.Coupled lateral-torsional vibration of rotor system trained by gears(Part I Analysis by transfer matrix method) [J].Bulletin of JSME,1984(27):271-277.

[2] SELLGREN U,KERBLOM M.A model-based design study of gearbox induced noise [C]∥Proceedings of the 8th International Design Conference Design 2004.Dubrovnik:Inderscience Publishers,2004:1337-1342.

[3] 王立华，李润方，林腾蛟，等.斜齿圆柱齿轮传动系统的耦合振动分析 [J].机械设计与研究，2002，18(5):30-32.

WANG Li-hua,LI Run-fang,LIN Teng-jiao,et al.Analysis for coupled vibration of helical gear transmission system [J].Machine Design and Research,2002,18(5):30-32.

[4] PARKER R G,AGASHE V,VIJAYAKAR S M.Dynamic response of planetary geare system using a finite element/contact mechanics model [J].ASME Journal of Mechanical Design,2000,122(6):305-311.

[5] LI Run-fang.Finite element solution to coupled thermo-elastic contact stress and impact response of meshing gears [J].Chinese Journal of Mechanical Engineering,1994,7(1):63-67.

[6] 杨振，王三民，刘海霞，等.负载与支承刚度对面齿轮传动系统动态特性的影响分析 [J].燕山大学学报,2010,34(4):293-300.

YANG Zhen,WANG San-min,LIU Hai-xia,et al.Influences of external load and supporting stiffness on nonli-near dynamics of face-gear transmission system [J].Journal of Yanshan University,2010,34(4),293-300.

[7] 朱才朝，陆波，宋朝省，等.大功率船用齿轮箱系统耦合非线性动态特性研究 [J].机械工程学报，2009，45(9):31-35.

ZHU Cai-chao,LU Bo,SONG Chao-sheng,et al.Research on nonlinear coupling dynamic characteristics of large burden marine gearbox [J].Journal of Mechanical Engineering,2009,45(9):31-35.

[8] 林腾蛟，蒋仁科，李润方，等.船用齿轮箱动态响应及抗冲击性能数值仿真 [J].振动与冲击，2007，26(12):14-17.

LIN Teng-jiao,JIANG Ren-ke,LI Run-fang,et al.Numerical simulation of dynamic response and shock resistance of marine gearbox [J].Journal of Vibration and Shock,2007,26(12):14-17.

[9] 杨成云，林腾蛟，李润方，等.增速箱系统动态激励下的响应分析 [J].重庆大学学报，2002，25(2):15-18.

YANG Cheng-yun,LIN Teng-jiao,LI Run-fang,et al.Response analysis of speed increase gearbox system in dynamic excitation [J].Journal of Chongqing University,2002,25(2):15-18.

[10] 林腾蛟，廖勇军，李润方，等.齿轮箱动态响应及辐射噪声数值仿真 [J].重庆大学学报，2009，32(8):892-896.

LIN Teng-jiao,LIAO Yong-jun,LI Run-fang,et al.Numerical simulation of dynamic response and radiation noise of gearbox [J].Journal of Chongqing University,2009,32(8):892-896.

[11] 王炎，马吉胜，蒙刚，等.齿轮系统刚柔耦合动力学建模与仿真研究 [J].机械传动，2009，33(4):32-35.

WANG Yan,MA Ji-sheng,MENG Gang,et al.The mo-deling and simulation research on rigid-flexible coupled gear system [J].Journal of Mechanical Transmission,2009,33(4):32-35.

[12] 刘辉，张喜清，项昌乐.多源动态激励下变速箱箱体结构的动态响应分析 [J].兵工学报，2011，32(2):129-135.

LIU Hui,ZHANG Xi-qing,XIANG Chang-le.Dynamic response analysis of gearbox housing under multi-source dynamic excitation [J].Acta Armamentarii,2011,32(2):129-135.

[13] 贺朝霞，常乐浩，刘岚.多耦合箱体振动的行星齿轮传动系统动态响应分析 [J].华南理工大学学报(自然科学版)，2015，43(9):128-134.

HE Zhao-xia,CHANG Le-hao,LIU Lan.Dynamic response analysis of planetary gear transmission system coupled with gearbox vibrations [J].Journal of South China University of Technology(Natural Science Edition),2015,43(9):128-134.

[14] 倪振华.振动力学 [M].西安：西安交通大学出版社，1990.

[15] CAI Y.Simulation on the rotational vibration of helical gears in consideration of the tooth separation phenomenon:A new stiffness function of helical involute tooth pair [J].ASME Journal of Mechanical Design,1995,117(9):460-468.

Supported by the National Natural Science Foundation of China(11672344)

DynamicResponseAnalysisofaTransmissionHousingUnderVariableSpeedConditions

ZANGMeng-yan1MENGNing1CHUShu-min2CHENYong3

(1.School of Mechanical and Automotive Engineering,South China University of Technology, Guangzhou 510640,Guangdong,China;2.Zhejiang Geely Automobile Institute Co.,Ltd.,Hangzhou 311228, Zhejiang,China;3.School of Mechanical Engineering,Hebei University of Technology,Tianjin 300130,China)

Based on the dynamic theory of the multi-body system, a dynamic model of a gear transmission system is constructed by taking into account the effects of the time-varying mesh stiffness, the tooth backlash, the bearing stiffness and damping, and the speed variation. Then, the dynamic meshing forces of gears and the dynamic forces of housing bearing seats are calculated, and after a flexible housing model is constructed, the natural frequency and modal shapes of the transmission housing are obtained. Finally, by taking the dynamic forces of the housing bearing seats as the excitation, the modal superposition method is adopted to calculate the dynamic response, thus acquiring the information relative to the vibration of the nodes on the housing surface. Simulation results show that, when a constant torque is applied, the vibration acceleration amplitude of the housing surface increases with the increase of the rotating speed, which accords well with the experimental results within a margin of error of 10%.

transmission; dynamic analysis; modal superposition method; dynamic response

2016-09-17

国家自然科学基金资助项目(11672344)

臧孟炎(1961-)，男，教授，博士生导师，主要从事CAE技术开发与应用研究.E-mail:myzang@scut.edu.cn

1000-565X(2017)08-0001-06

U 463.212

10.3969/j.issn.1000-565X.2017.08.001