概率统计中的误区警示

■宁夏银川二中 马丽欣

概率统计中的误区警示

■宁夏银川二中 马丽欣

编者的话:同学们在学习的过程中,难免会出现错解的现象。本期"易错题归类剖析"栏目推出的文章,注重剖析错解原因,注重补充知识缺陷,注重题目引申变换,希望同学们认真领会,学以致用,不再发生类似的错解。

在概率统计学习中,由于同学们对概念理解不透、审题不严、考虑不周或忽视公式成立的条件等,常容易导致求解中出现 “多解”或“漏解”等失误。本文对概率统计中常见的易错、易混的典型题归类整理,并进行错解剖析和警示展示,希望对同学们的学习有所帮助。

误区1——混淆“互斥事件”与“对立事件”

例1 某城市有两种报纸甲报与乙报供居民们订阅。记A=“只订甲报”,B=“至少订一种报”,C=“至多订一种报”,D=“不订甲报”,E=“一种报也不订”,则下列事件是互斥事件且是对立事件的为____。

①A与C;②B与E;③B与D;④B与C;⑤E与C。

错解:选①或③或④或⑤。

剖析：“互斥”与“对立”混同,要准确解答这类问题,必须搞清对立事件与互斥事件的区别和联系。

正解：由互斥事件和对立事件的定义知② 是互斥事件,也是对立事件,故选②。

警示：“互斥事件”和“对立事件”是针对两个事件而言的,互斥事件是指事件A与事件B在任何一次试验中不会同时发生,包括三种不同的情形:① 事件A发生且事件B不发生;② 事件A不发生且事件B发生;③事件A与事件B同时不发生。而对立事件是指事件A与事件B有且仅有一个发生,包括两种情形:①事件A发生,事件B不发生;② 事件B发生,事件A不发生。

误区2——混淆“条件概率P(B|A)”与“积事件概率P(A·B)”

例2 袋中有6个黄色、4个白色的乒乓球,作不放回抽样,每次任取一球,取2次,求第二次才取到黄色球的概率。

错解:记“第一次取到白球”为事件A,“第二次取到黄球”为事件B,“第二次才取到黄球”为事件C,所以P(C)=P(B|A)

剖析：上面解法错误在于没有弄清P(A·B)与P(B|A)的含义。P(A·B)表示在样本空间S中,A与B同时发生的概率,而P B|A( )表示在缩减的样本空间SA中,作为条件的A已经发生的条件下事件B发生的概率。

警示：正确理解条件概率和相互独立事件同时发生的概率的关系,借助古典概型概率公式分别求P(A)和P(A·B),得P(B|A)=,这是求条件概率的通法。

误区3—— 混淆 “有序”与“无序”

例3 甲、乙两人参加普法知识竞赛,共有1 0道不同的题目,其中选择题有6道,判断题有4道,甲、乙两人依次各抽取1题。

(1)求甲抽到选择题、乙抽到判断题的概率。

(2)求甲、乙两人至少有1人抽到选择题的概率。

(2)设甲、乙两人至少有1人抽到选择题book=29,ebook=31为事件A,则甲、乙两人都未抽到选择题为事件A,由对立事件的计算公式得P(A)=1-

剖析：上述解法把甲、乙依次抽取1题理解为甲、乙同时抽取1题,前者与顺序有关,是排列问题,而后者与顺序无关,是组合问题,两者是不同的。

正解：基本事件总数应为A210,正确的结果应为:

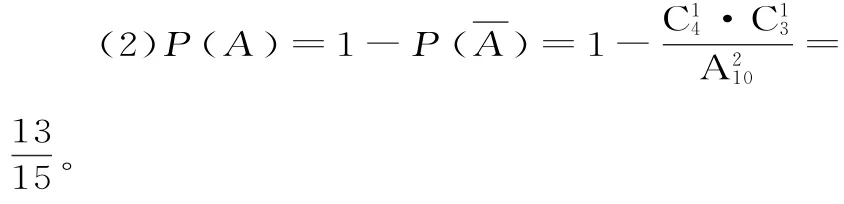
警示：求概率关键是借助排列数和组合数进行计数,区别排列与组合的方法是拿出一种结果交换其顺序,结果变化与顺序有关属于排列,没有变化与顺序无关属于组合,在概率题中经常会碰到有关排列与组合的区分问题。

误区4——混淆抽取中的“有放回”与“无放回”

例4 把大小和形状完全相同的五个小球编号为1,2,3,4,5,放在一个箱子中充分混合,有放回地抽取两次,求取出编号为2和4的小球的概率。

错解1:取出的两个小球的所有可能结果为(1,2),(1,3),(1,4),(1,5),(2,1),(2,3),(2,4),(2,5),(3,1),(3,2),(3,4),(3,5),(4,1),(4,2),(4,3),(4,5),(5,1),(5,2),(5,3),(5,4),共2 0种可能情况,每种情况都等可能出现。事件A“取出的是编号为2和4的小球”对应于基本事件(2,4)和(4,2),故所求概率P(A

错解2:有放回地连续抽取两次,所有可能结果为(1,1),(1,2),(1,3),(1,4),(1,5),(2,2),(2,3),(2,4),(2,5),(3,3),(3,4),(3,5),(4,4),(4,5),(5,5),共1 5种情况。事件A“取出的是编号为2和4的小球”对应于基本事件(2,4),共1种可能情况,故所求概率

剖析：本题是有放回地抽取小球,且抽取两次小球是有序的。错解1中忽略了(1,1),(2,2),(3,3),(4,4),(5,5)这5种情况。错解2中忽略了抽取两次小球是有顺序的,即(1,2)和(2,1)表示的是不同的事件。

正解：有放回地连续抽取两次,必须考虑抽取顺序,所有可能结果为5×5=2 5(种),事件A“取出的是编号为2和4的小球”对应的基本事件为(2,4)和(4,2),故所求概率

警示：有放回抽取样本必须考虑抽取顺序,无放回抽取样本可以考虑抽取顺序,也可以不考虑抽取顺序,当作一次性抽取。常常构建有序实数对的基本事件空间使“无序”转化为“有序”。

误区5——混淆几何概型中的“测度”单位

例5 如图1,在R t△A B C中,∠A=3 0°,过直角顶点C作射线CM交线段A B于点M,求使|AM|>|A C|的概率。

错解:设事件M为“作射线CM,使|AM|>|A C|”,在A B上取点C'使|A C'|=|A C|,因为△A C C'是等腰三角形,所以|C'B|=(2-3)|A B|,则P(M)=

图1

剖析：错解是以长度为“测度”导致M在A B上的落点不是等可能的,而射线CM落在∠A C B内的任意位置是等可能的。

正解：在∠A C B内作射线CM是等可能的,基本事件是射线CM落在∠A C B内任一处,使|AM|>|A C|的概率只与∠B C C'的大小有关,这符合几何概型的条件。设事件D为“作射线CM,使|AM|>|A C|”。在A B上取点C'使|A C'|=|A C|,因为△A C C'是等腰三角形,所以 P(D)=

警示：合理选择几何“测度”使“非等可能”转化为“等可能”。计算公式P(A)=,凸显几何概型的“无限性”和“等可能性”。

误区6——混淆二项分布与超几何分布

例6 (2 0 1 7年枣庄市高三期末)已知甲、乙两名篮球运动员每次投篮命中的概率分别为、p,甲、乙每次投篮是否投中相互之间没有影

(1)求p的值;

(2)若甲投篮1次、乙投篮2次,两人投篮命中的次数的和记为X,求X的分布列和数学期望E(X)。

所以X的分布列为表1。

表1

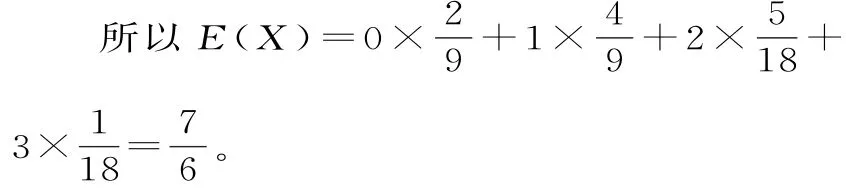
剖析：(1)对二项分布中各参数含义不清导致p求错。(2)对随机变量X的取值的意义理解出错,应借助变量X的取值合理分类,每类下借助相互独立事件同时发生分步,每步中构建二项分布P(X=k)=Cknpk(1-p)k,k=0,1,2,…,n,从而简化求解概率。

正解：(1)乙每次投篮命中的概率为p,投篮3次,命中次数ξ～B(3,p),由题意得,

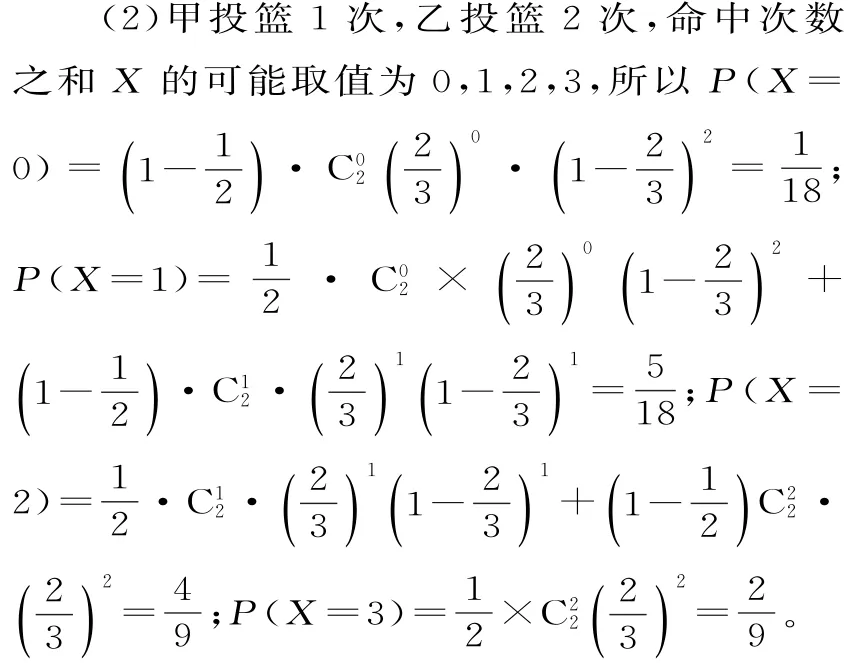
所以X的分布列为表2。

表2

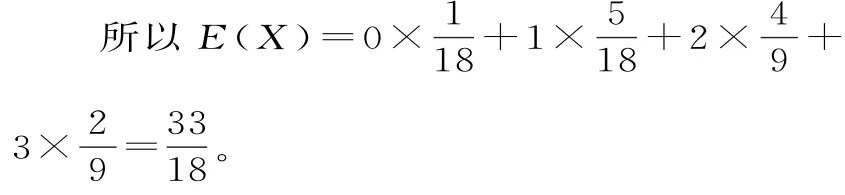
警示：设在每次试验中成功的概率都为p,则在n次重复试验中,试验成功的次数用ξ来表示,ξ服从二项分布,则在n次试验中恰好成功k次的概率为Pξ=k( )=Cknpk(1-p)n-k,则E(ξ)=n p,D(ξ)=n p(1-p)。超几何分布是在理解随机变量的意义下,把元素自然分成2组,利用组合数和古典概型概率公式得到分布列的一个通项公式,其本质是“不放回抽样”,是一种古典概型,而二项分布的随机实验是“独立重复实验”,强调每次实验的结果发生的概率相同,可认为是“有放回抽样”。

(责任编辑 王福华)