对一道利用导数证明对数不等式问题的反思

■郑州市第十一中学1 8 0 5班 李洁莹

对一道利用导数证明对数不等式问题的反思

■郑州市第十一中学1 8 0 5班 李洁莹

笔者在对导数知识进行复习时经常遇到导数证明不等式的问题,这也是高考经常出现的问题之一。但由于综合性较强,往往成为我们得分的一大障碍。本文通过一道例题的不同思考角度,给出常规解决思路。

(1)当a=1时,求f(x)在x∈[1,+∞)上的最小值;

(2)若f(x)存在单调递减区间,求a的取值范围;

(2)解法1:(分类讨论)由题意得f'(x)在x∈(0,+∞)上有负值区间。

当a<0时,g(x)=a x2+2(a-1)x+a的开口向下,在x∈(0,+∞)上 一 定有负值区间。

所以h'(x)在x∈(0,1)上有h'(x)<0,在x∈(1,+∞)上有h'(x)>0。

所以h(x)min=h(1)=

评注:解法1为常规思路,考虑导数有负值区间情况,对导数分类讨论;解法2非常巧妙地避开了容易出现恒成立问题的陷阱,转化为特称命题的证明,给人耳目一新的感觉。

(3)解法1:(构造数列)设数列{an}的前n项和Sn=l n(n+1),则an=Sn-Sn-1=l n(n+1)-l nn=l n

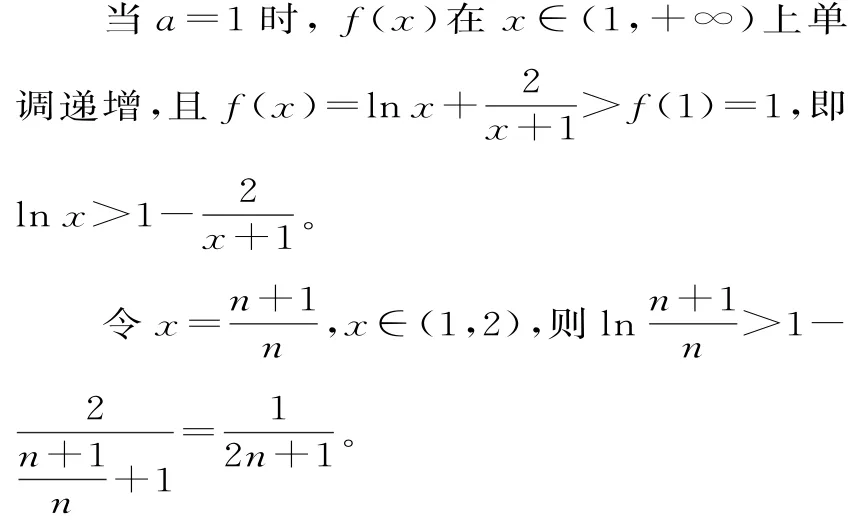
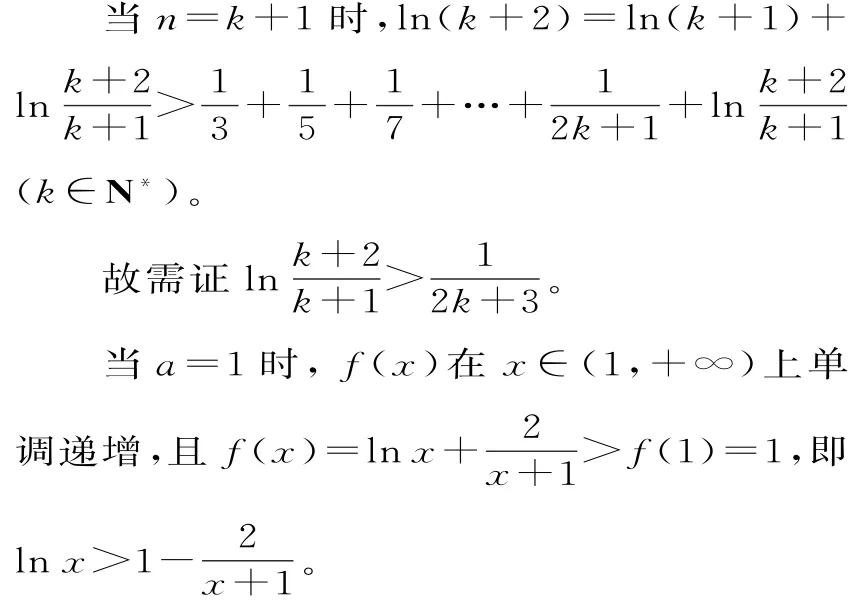
由①②得,原不等式成立。

评注:将上述两种方法比较可知,解法1是构造新数列,通过比较新数列与原数列通项大小证明不等式的,是一种常规思路;解法2的数学归纳法是同学们经常使用的办法,但不容易结合第(1)问证明。

这道例题的后两问都是用了两种方法,从不同角度求解证明,较好地体现了数学思想和数学方法的统一。在平时的学习中,我们要注意培养从不同角度分析问题的意识,尝试用多种方法解题,寻找最佳解题方法,掌握通性通法。只有这样,在解题时才能游刃有余。

(责任编辑 刘钟华)