拓扑切换的多传感器网络化系统分布式H∞滤波

池小波, 张利利, 贾新春

(山西大学 数学科学学院, 山西 太原 030006)

0 引言

随着无线传感器网络(WSN)在环境监测,智能电网,智能交通系统等领域中的广泛应用[1],基于传感器网络的分布式滤波或估计问题受到越来越多学者的关注[2-4].分布式滤波系统中传感器自身采集数据的同时,相邻节点间可以通过网络共享数据[2-5].因此,如何处理传感器间数据共享导致的网络特征和复杂耦合问题成为分布式滤波器设计的最重要的问题之一.实际应用中WSN的网络拓扑通常受多种因素的影响,例如节点故障、障碍物阻挡、环境以及其他网络诱导因素[1].因此,分布式滤波器的设计应考虑网络拓扑的变化[6,7].

据作者所知,有关拓扑切换的分布式滤波器的文献中很少有对其拓扑切换时刻的分析.另一方面,数据丢包,能量和带宽约束也是在WSN中需要考虑的要素之一[1].当两个采样数据之间存在微小波动,或者系统状态接近平衡态时,使用传统的周期采样传输方案会产生大量冗余包.为了克服传统数据传输方案的缺点,近年来,提出了离散事件触发传输方案[8].由于其能保持一定的系统性能,同时有效的降低传输负载而受到广泛的关注,参见文献[8-11].其次,针对数据丢包问题,大多数工作都是为了减小WSN中单信道丢包产生的影响[11].然而,为了保证通过事件触发机制传输的数据的可靠性,冗余信道的加入将有助于解决丢包问题,甚至减轻部分信道断开的影响[12，13].因此,在WSN中使用冗余信道来设计分布式滤波器是非常必要和重要的.据作者所知,关于具有冗余通道和事件触发传输机制的多传感器网络化系统的分布式H∞滤波问题迄今少有研究.

本文研究了具有网络拓扑和事件触发传输机制的多传感器网络化系统的分布式H∞滤波问题.主要贡献概括如下:(1)提出了一个新的监测机制来辨识拓扑切换时刻.并利用随机Markov链来表示若干拓扑模态切换过程.(2)基于拓扑切换时刻的采样数据提出了一类分布式事件触发传输方案.(3)同时考虑双通道数据丢包,拓扑切换和事件触发传输方案,将网络化滤波误差系统建模为随机时延系统.同时提出了一种事件触发参数和滤波器增益的协同设计方法.

1 问题描述

考虑一类多传感器网络化分布式滤波系统,如图1所示.利用多个传感器节点分别采集待估计系统的输出yi(i=1,2,…,n),并用于估计系统的信号.图1中的变量参见模型(1)和(2).每个传感器节点都分别由传感器、零阶保持器(ZOH)、滤波器、采样器、分布式数据处理器(DDP)和存储器组成.其中,传感器用于采集系统(1)的输出,采样器用于采集滤波器的状态,DDP用于检测事件触发条件来决定数据是否传输,存储器包含多个存储单元,可以检测新到达数据包的时间戳和ID,用来存储最新接收的采样状态,同时主动丢弃非邻居节点的过时数据.这里各节点之间依赖于WSN的拓扑结构进行通信.本文引入冗余信道2来保证被触发滤波器状态传输的可靠性.

图1 多传感器网络化分布式滤波系统

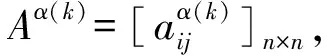
考虑如下的线性离散系统

(1)

式(1)中：x(k)∈Rnx和z(k)∈Rnz为系统状态和待估计系统信号,w(k)∈Rnw为外部干扰,满足w(k)∈l2[0,∞),矩阵A,B和M是适当维数的常值矩阵,x(0)=x0.

传感器i的噪声输出观测模型如下

yi(tk)=Cix(tk)+Div(tk)

(2)

式(2)中：yi(k)∈Rny是节点i的采样数据,v(k)∈Rnv为测量噪声,满足v(k)∈l2[0,∞),假设w和v相互独立.矩阵Ci和Di是适当维数的常值矩阵.tkh,k∈N表示由拓扑切换时刻决定的采样时刻.

注许多因素可能导致网络拓扑结构频繁的改变.因此,这里假设传感器只在网络拓扑切换时刻进行采样是合理的.下一小节将给出拓扑切换监测机制,用来识别切换时刻tkh.

随机变量ai(k)和bi(k)分别表示主通道和冗余通道的数据包丢失现象,假设ai(k)和bi(k)均为Bernoulli分布的随机序列,并满足

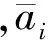
1.1 拓扑切换监测机制和切换模型

无线传感器网络由分布在监测区域内的大量传感器节点组成,如图1所示.每个节点除了要采集待估计系统的数据以外,还要将收集到的数据进行一定的处理，之后将处理后的数据通过无线通道以单跳的方式传输至邻居节点,但由于许多因素可能导致网络拓扑结构的改变,因此需要对邻居节点集进行监测.又因为无线传感器网络是以计算机为基础的数字网络,因此本文做如下假设:

(1)假设每个节点的集被周期性监测,监测时刻序列为Q1={0,h,…,kh,…} ,其中k∈N,传感器i只有在网络拓扑切换时刻才进行采样.

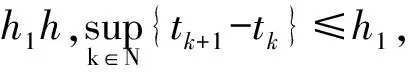
为了识别拓扑切换时刻,本文引入如下监测机制:在kh时刻,WSN中的所有传感器节点都发送具有ID的HELLO包,其中,邻居节点之间通过HELLO包相互通信,节点从邻居节点收到HELLO包,记录下每个包中所有节点的ID,最后形成该节点的邻居节点集.通过监测每个节点的邻居节点集的变化来识别拓扑切换时刻tkh.

根据上述拓扑切换监测机制,可以获得切换拓扑时刻序列.考虑实际应用中多传感器网络拓扑切换的随机性,利用Markovian随机模型来表示拓扑模态的切换,定义马尔科夫链α(tk)取值于Λ={1,2,…,q},且转移概率矩阵为Π=[πrs] ,其中r,s∈Λ表示马尔科夫模式,其转移概率如下:

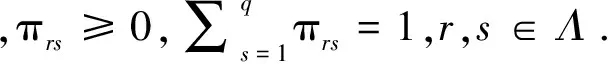
1.2 基于拓扑切换的分布式事件触发机制

为了使用相邻滤波器的数据来估计系统的信息同时节省WSN中受限资源的使用,本文提出一个基于WSN的数据传输机制来收集邻居滤波器的采样数据.具体如下：

Ri(k)∶=

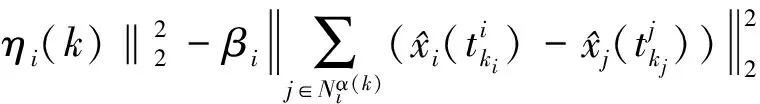
(4)

(5)

1.3 分布式滤波

基于事件触发传输机制和拓扑切换模型,设计分布式滤波模型如下：

(6)

式(6)中：

cj(k)=aj(k)χ(k)-(1-aj(k))bj(k)χ(k),

定义dk=k-tk,k∈[tk,tk+1)且满足0≤dk≤h1.

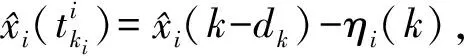
(7)

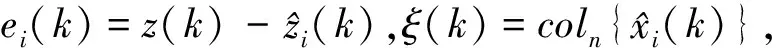
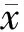
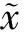
由以上结论得到滤波误差系统如下：

(8)

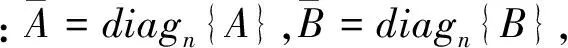
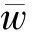
Γ(k)=diagn{ai(k)I},

W(k)=Γ(k)+(I-Γ(k))Υ(k),

Υ(k)=diagn{bi(k)I},α(k)=r,

t∈[tk,tk+1),r∈Λ.

由式(7)可得

(9)

E{‖φ(k)‖2}≤λσkE{‖φ(θ)‖2}

(10)

本文的主要目标是设计分布式H∞滤波器(6)和事件触发参数βi,使得系统(8)满足以下条件：

(2)在零初始条件下,滤波误差e(k)满足

(11)

2 主要结果

2.1 分布式H∞滤波性能分析

定义如下的李雅普诺夫泛函

(12)

式(12)中：

Hij=Hi-Hj,I2=[0,I],Pr>0,

r∈Λ,Q1>0,R1>0,

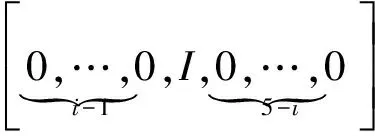
φ1(k)=

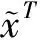
下面先介绍一个引理，用于定理的证明

引理[14]对于给定的正整数m,n,η∈(0,1)和矩阵W1,W2,R>0,对定义域Rm上的任意向量φ(k)定义函数f(η,R)为

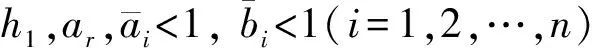
(13)

(14)

(15)

式(14)中：

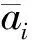
证明:考虑到切换时刻可能大于离散系统的运行时刻,因此存在两种情况:(1)系统的运行时刻就是切换时刻;(2)系统的运行时刻不是切换时刻.下面分别考虑系统运行时刻是否与随机切换时刻匹配的两种情形.

情形1当k=tk+1-1,k+1=tk+1时,网络拓扑将发生切换,则令α(k)=r∈Λ,沿轨迹(8)作V(k)的前向差分,有

ΔV1=E{V1(k+1)}-V1(k)=

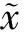
(16)

ΔV2=E{V2{k+1}}-V2(k)=

(17)

ΔV3=E{V3(k+1)}-V3(k)=

R1ϑ(k+u)}

(18)

利用Jensen不等式的性质,有

由引理得

(19)

由式(18)和(19),可得

(20)

(21)

式(21)中：

由(14)式和Schur补引理可知Σr<0,因此,有

ΔV(k)<-λmin(-Σr)‖φ1(k)‖2

(22)

其中,λmin(-Σr)是-Σr的最小特征值.根据文献[15]的引理1可知,滤波误差系统(8)是均方意义下指数稳定的.

接下来,将进行分布式H∞滤波性能分析,假设在零初始条件下,利用(20)有

[V(k+1)-V(k)]}-V(N+1)≤

(23)

式(23)中：

情形2当k∈[tk,tk+1-1),k+1≠tk+1时,网络拓扑保持不变,类似情形1的证明,可以得到式(15).证毕.

根据定理1,下面将给出分布式滤波(6)的设计方法.

2.2 滤波器参数设计

(24)

(25)

(26)

式(25)中：

3 仿真例子

考虑下面的离散线性系统

(27)

其中,系统初始状态为x0=[1.3 2.5],外部干扰选取w(k)=e-2k.利用3个传感器节点分别采集待估计系统的输出,每个传感器的量测模型为(2),其中C1=[-0.1 1],C2=C3=[-2 1],D1=D2=1,D3=0.15,v(k)=e-ksin(2k).

假设网络在以下两个拓扑模态下进行切换,其邻接矩阵对应如下：

基于以上参数和事件触发条件(4),利用Matlab中的Simulink模块进行仿真,其中实际输出z(k)和各个滤波器的输出估计值如图3所示.从图3可以看出,从12 s之后系统输出信号及其各滤波器估计值的轨迹基本重合,说明本文所设计的方法是有效的.图4表示了三个滤波器节点的两个连续传输时刻之间的时间间隔,基于文献[8]中的方法,可计算出3个滤波器之间的数据包传输率约为60.32%，这意味着通讯资源可节省39.68%,由此可以看出采用事件触发策略可以减少数据传输率.

图2 传感器网络的拓扑模态切换策略

图3 系统输出信号及其估计值

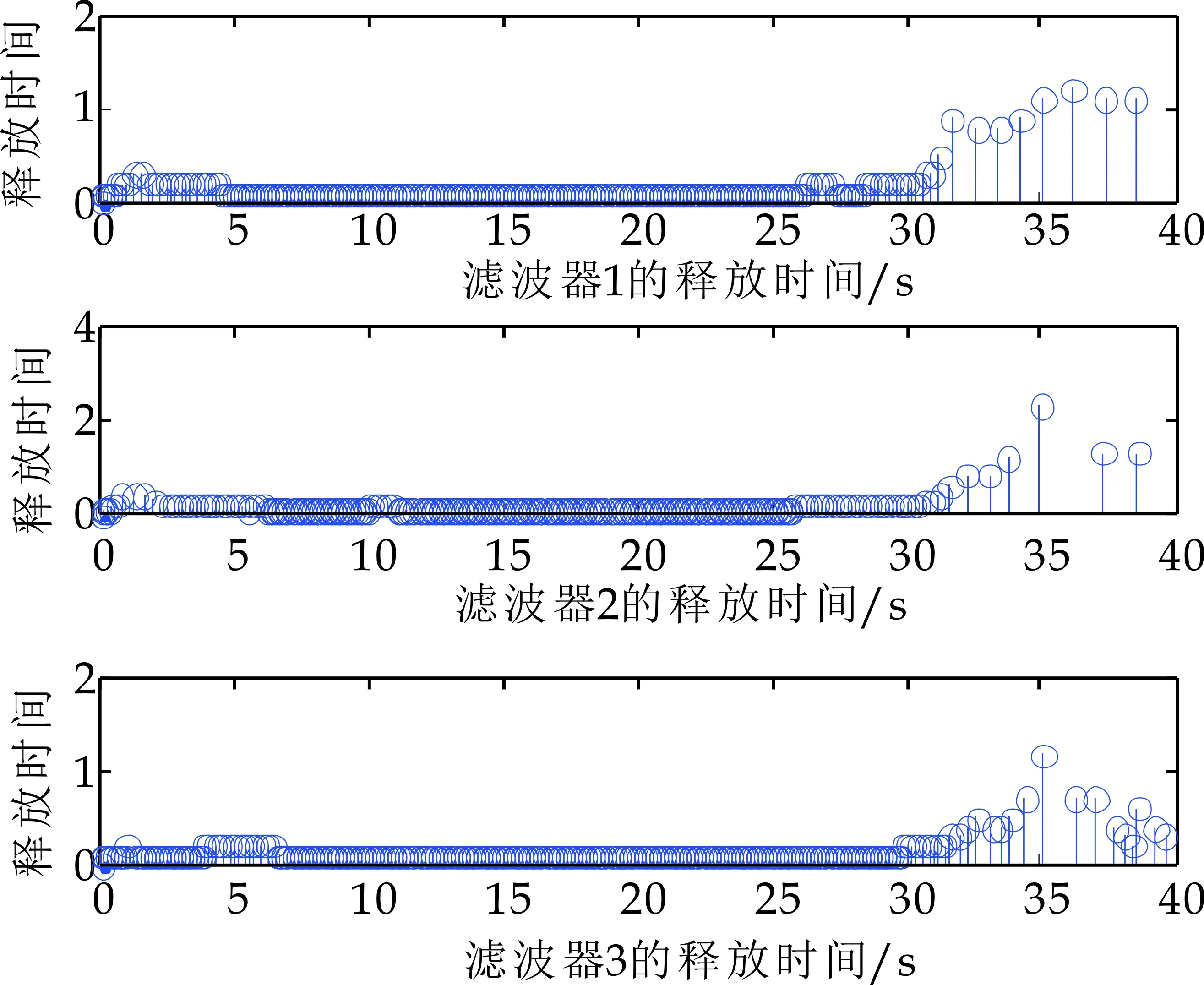
图4 两个连续释放时刻的释放时间间隔

4 结论

本文研究了一类具有丢包、拓扑切换和事件触发方案的WSN下的分布式滤波问题,并提出了一种滤波器增益和触发参数的协同设计方法.接下来将进一步研究具有采样机制和拓扑切换异步的传感器网络系统的分布式滤波问题.

[1] Yick J,Mukherjee B,Ghosal D.Wireless sensor network survey[J].Computer Networks,2008,52(12):2 292-2 330.

[2] Ge X H,Han Q L,Jiang X F.Distributed H∞filtering of sensor networks with/without asymmetric intercommunication delays[C]//2013 IEEE International Symposium on Industrial electronics.Taiwan:IEEE Industrial Electronics Society,2013:1-6.

[3] Matei I,Baras J S.Consensus-based linear distributed filtering[J].Automatica,2012,48(8):1 776-1 782.

[4] Ding D R,Wang Z D,Shen B.Recent advances on distributed filtering for stochastic systems over sensor networks[J].International Journal of General Systems,2014,43(3-4):372-386.

[5] Zhang X M,Han Q L,Yu X H.Survey on recent advances in networked control systems[J].IEEE Transactions on Industrial Informatics,2016,12(5):1 740-1 752.

[6] Liu B,Zhang X M,Han Q L.Event-triggered distributed H∞filtering for networked systems with switching topologies[C]//2015 IEEE 13th International Conference on Industrial Informatics.Cambridge,United Kingdom:IEEE Industrial Electronics Society,2015:162-167.

[7] 于海洋.传感器网络中的分布式H∞滤波方式[D].大连:大连理工大学,2014.

[8] Yue D,Tian E G,Han Q L.A delay system method for designing event-triggered controllers of networked control systems[J].IEEE Transactions on Automatic Control,2013,58(2):475-481.

[9] Zhang H,Hong Q Q,Yan H C,et al.Event-based distributed H∞filtering networks of 2-DOF quarter-car suspension systems[J].IEEE Transactions on Industrial Informatics,2017,13(1):312-321.

[10] Liu Q,Wang Z D,He X,et al.Event-based recursive distributed filtering over wireless sensor networks[J].IEEE Transactions on Automatic Control,2015,60(9):2 470-2 475.

[11] Zhang H,Zheng X Y,Yan H C,et al.Codesign of event-triggered and distributed H∞filtering for active semi-vehicle suspension systems[J].IEEE/ASME Transactions on Mechatronics,2017,22(2):1 047-1 058.

[12] Ding D R,Wang Z D,Shen B,et al.Envelope-constrained H∞filtering with fading measurements and randomly occurring nonlinearities:The finite horizon case[J].Automatica,2015,55:37-45.

[13] Zhang L X,Ning Z P,Wang Z D.Distributed filtering for fuzzy time-delay systems with packet dropouts and redundant channels[J].IEEE Transactions on Systems,Man and Cybernetics:Systems,2016,46(4):559-572.

[14] Park P G,Ko J W,Jeong C.Reciprocally convex approach to stability of systems with time-varying delays[J].Automatica,2011,47(1):235-238.

[15] Wang Z D,Yang F W,Liu X H,et al.Robust H∞filtering for stochastic time-delay systems with missing measurements[J].IEEE Transactions on Signal Processing,2006,54(7):2 579-2 587.