基于流场探测的发动机喘振控制仿真研究

梁俊龙，王玉峰，张贵田

(1.西北工业大学 燃烧、热结构与内流场重点实验室，陕西 西安 710072； 2.西安航天动力研究所，陕西 西安 710100)

基于流场探测的发动机喘振控制仿真研究

梁俊龙1，王玉峰2，张贵田1

(1.西北工业大学 燃烧、热结构与内流场重点实验室，陕西 西安 710072； 2.西安航天动力研究所，陕西 西安 710100)

为使冲压发动机性能最优并始终工作在安全状态，需要使其工作的喘振裕度最小且在喘振边界内。在喘振边界安装一种能够准确分辨超声速或亚声速流场状态的流场探测装置，控制进气道结尾激波位置。针对一维变截面流动控制方程，研究了流场探测装置的安装位置，以及激波越过流场探测装置后控制系统的减油规律。仿真研究结果表明，用试验数据修正理论仿真的方法可以准确地捕捉进气道结尾激波，同时根据某型冲压发动机的设计临界喘振裕度，确定了流场探测装置安装位置位于距进气道锥尖的距离；进气道沿程压力跟随发动机燃油流量的变化而变化，压力波传播时间相对于燃油调节时间可以忽略；由于进气道内激波前后运动存在明显的压力滞环现象，当激波越过喘振边界时，进气道出口压力会进一步上升，发动机喘振危险加大，应使用加速电磁阀快速减小燃油流量，控制激波回到安全区域。

冲压发动机；激波探测；喘振控制；仿真

0 引言

液体亚燃冲压发动机工作时，来流状态参数和燃烧室供油流量的变化会导致进气道结尾激波的前后运动。当结尾激波向进气道出口方向运动时，进气道喘振裕度增大，进气道的总压恢复系数降低，发动机性能下降；当结尾激波向进气道唇口方向运动时，进气道总压恢复系数提高，发动机性能提高。然而，一旦进气道结尾激波越过进气道喉道，发动机很容易进入喘振状态。因此，为保证发动机始终工作在安全状态，发动机控制规律设计时必须考虑喘振保护边界限制条件。

超声速进气道的喘振现象自1944年Oswatitsch[1]发现以来，一直备受科技工作者的重视。人们进行了大量的理论分析[2]、数值研究[3-5]和试验研究[6-11]工作，给出了进气道的喘振特征、喘振发展以及喘振时进气道唇口和喉道段流动特征的研究结果。在喘振机理研究上，研究者基本上都认为喘振是由气流分离引起正激波振荡这一机理，引起气流分离的原因可能是压缩面气流分离或斜激波与正激波相交，在交点处出现一个上下速度不连续的滑流层而产生的。由于喘振的危害性巨大，发动机控制规律必须考虑喘振保护，国内外进行了大量的喘振控制[12-17]，一般都是将发动机偏差模型、进气道及导弹或飞行器模型综合在一起，构成导弹或飞行器与发动机的一体化数学模型而进行发动机喘振保护控制。

本文主要是基于一种流场探测装置来辨别流场状态，该装置是具有特定气动型面的微型气动元件，试验表明对探测主流场扰动可以忽略，一般安装在主流道的径向中心位置，通过测量气动元件不同位置的压力可以准确分辨出所处的流场状态为超声速流场或亚声速流场。当流场探测装置处于超声速流场时，认为发动机的工作状态比较安全；当流场探测装置处于亚声速流场时，表明激波已越过流场探测装置向唇口方向运动，发动机进入危险工作状态。采用基于流场探测装置的喘振控制，可以对冲压发动机工作的超临界状态进行实时控制，使冲压发动机的性能发挥至最优。本文通过数值方法研究了在发动机燃烧室背压扰动下流场探测装置的安装位置，以及激波越过流场探测装置后控制系统的减油规律，以保证激波可以重新回到安全位置。

1 计算模型、控制方程及计算方法

1.1 计算模型

计算模型为轴对称头部进气固定几何结构的冲压发动机进气道喉道至进气道出口段。图1给出了计算模型的截面几何流通面积随轴向相对位置的变化曲线，其中，坐标原点为进气道的理论锥尖，x轴为轴向相对位置(当前位置与进气道长度的比值)，y轴为截面几何流通面积。

1.2 控制方程

为简化分析，假设气体为理想气体，一维变截面无粘流动的控制方程为：

(1)

为数值计算的统一性和一般性，对控制方程进行无量纲化，取喉部面积、入口密度、声速和进气道长度作为参考值，对面积、密度、速度、时间及长度进行无量纲化。令：

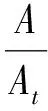
(2)

方程经无量纲化处理后，为简化方程，令:

(3)

经过上述简化，控制方程可简化为：

(4)

令U=[u1,u2,u3]T，F=[f1,f2,f3]T，J=[j1,j2,j3]T，则控制方程可进一步简化为：

∂U/∂t+∂F/∂x′=J

(5)

1.3 计算方法

利用二阶精度的空间Marcomack格式进行求解，该格式包括预测步和校正步，计算格式如下：

(6)

其中，粘性修正项为：

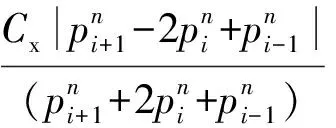
(7)

式中常数Cx为粘性修正系数，通常取0～1，数值越大粘性耗散越强，数值稳定性越好。

时间和空间步长应当满足CFL条件。进气道入口为超音速气流，入口边界条件固定；出口为亚音速状态，给定压力、密度或者速度三者中的任意一个均可，文中给定出口压力。

入口的边界条件为：

(8)

亚音速出口边界条件为：

(9)

对于固定几何结构的冲压发动机，发动机的设计点是冲压发动机性能发挥最好、喘振余量最小的点，而对于其他工作状态点，发动机均工作在超临界工作工作，因此，本文的研究着重关注发动机的设计状态点。

选取发动机设计的高度和马赫数状态点，根据该状态点进气道吹风的试验结果，在出口背压为0.85 MPa时进气道处于临界工作状态。计算采用的CFL数为0.6，人工粘性系数选取为0.6，收敛标准为密度残差小于10-5。

在发动机设计状态点的临界工作状态时，图2给出了计算得到的进气道沿程马赫数随轴向位置的变化曲线。可以看出，结尾激波前的马赫数在1.8左右，进气道出口直段马赫数约为0.432。进气道结尾激波距进气道锥尖的相对位置为0.227，距进气道喉部的相对位置为0.124，激波位置距离进气道喉部较远，此时进气道处于超临界而非临界工作状态，出现此现象的原因主要是没有考虑进气道内的摩擦阻力损失。

为确保计算的精确性，在控制方程中增加了摩摩擦阻力项，公式(1)中的动量方程的右端项变为：

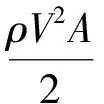
(10)

f=f1(lgRe)-2.58/(1+0.5Ma2)0.467

为了确定摩擦阻力系数值，以发动机处于该工作高度和马赫数状态时进气道临界状态为标准状态，来计算摩擦阻力系数值。图3给出了在不同的摩擦阻力系数下进气道的激波位置。可以看出，当摩擦阻力系数取为a2时，激波位置位于进气道喉道位置，与临界状态进气道的激波位置一致。因此，下文计算时选取的摩阻系数为a2。

2 仿真计算及结果分析

2.1 流场探测装置安装位置仿真研究

当发动机推力需求增大使燃烧室供油流量增大、室压提高时，进气道结尾激波位置前移越过流场探测装置时，探测装置能够及时准确地捕捉到流场状态的变化，并开始使发动机按预定的供油规律减少燃烧室的供油流量，必要时该燃油流量需要持续一定时间。如果激波仍然没有返回到安全位置，在该油量基础上进一步减少燃油流量。

根据上述喘振控制规律的要求，流场探测装置位置应该为发动机在设计高度和马赫数时进气道工作在临界喘振裕量时的进气道结尾激波位置。由进气道吹风试验结果，在该马赫数下进气道出口压力为0.795 MPa时达到临界喘振裕量，由定常计算结果可得进气道的激波位置见图4。可以看出，发动机达到临界喘振裕度时的结尾激波位置约在距进气道头锥的相对位置为0.192，该位置就是流场探测装置的安装位置，也就是冲压发动机的喘振保护边界，此时进气道的出口平直段的马赫数约为0.454。

2.2 燃烧室压力变化时进气道的压力响应特性

对于工作在某个确定状态的固定几何结构的冲压发动机来说，发动机供油流量的突然增加会导致燃烧室压力的突然跃升。这里仿真计算进气道的压力响应特性时暂不考虑燃油调节装置的控制调节时间，首先假定燃烧室压力阶跃增加。下面对不同的燃烧室压力扰动下进气道沿程压力的动态响应特性进行了研究。

在发动机设计状态的临界喘振余量下，燃烧室压力阶跃变化3%，6%及9%，图5距进气道锥尖轴向相对位置0.186处压力测点的响应情况。

该处压力测点位于结尾激波前，由图5可以看出，当进气道出口压力阶跃变化时，经过一定时间后，激波越过该测点，测点压力迅速升高。但是，不同的燃烧室压力扰动量，同一测点压力扰动的时滞是不同的。对于3%，6%及9%的压力扰动，其时间延迟分别为0.0153 s，0.013 85 s和0.013 25 s。压力扰动量越大，时间延迟越小；压力扰动波在通道内的传播速度与当地声速和激波运动时间有关，而激波运动速度与激波前后压比关系较大，当扰动量较大时，压比较大，故激波运动速度较快，时间延迟较短。

当冲压发动机实际工作时，由燃油调节指令发出到燃烧室室压爬升到额定值，该过程中室压的变化并非是阶跃增加的。图6给出了某次发动机试验中燃油流量调节指令和实际的燃油流量调节曲线，可以看出，实际燃油流量调节相对指令延迟0.1 s，从2.5 kg/s到3.0 kg/s耗时0.25 s，相对于发动机的燃油调节控制时间，进气道出口压力扰动引起的激波延迟时间几乎可以忽略不计。

当发动机的燃油流量按一定的调节特性调节3%的进气道出口压力时，发动机进气道出口压力按图8所示的曲线进行变化。图7和图9中给出了进气道的结尾激波后(距进气道锥尖相对位置0.222处)和结尾激波前(距进气道锥尖相对位置0.186处)的压力变化曲线，图8给出了激波位置随时间变化曲线。

由计算结果可以看出，当进气道出口压力按发动机供油控制的某调节特性变化时，结尾激波后的压力可以迅速响应，其变化趋势与出口压力基本相同。但是，结尾激波前的压力在出口压力开始爬升0.15 s后才开始爬升，结果表明燃烧室压力变化缓慢时，激波向前的运动速度较慢。也就是说，如果燃烧室的燃油供应量增大，从燃油流量开始增大到流场探测装置监测到激波越过流场探测装置所需的时间较长，一旦判断出激波越过流场探测装置，也会有较长的反应时间来减小油量，从而使激波重新回到安全位置。

2.3 喘振控制仿真计算

当发动机的燃油流量增大，燃烧室压力提高，进气道结尾激波越过流场探测装置后，意味着发动机即将发动机喘振，此时需要降低发动机燃烧室的供油流量。喘振控制规律需要确定激波越过流场探测装置后的供油流量减小比例以及燃油流量减小的快速性，以给发动机控制系统设计提供参考。

在发动机设计状态，进气道结尾激波位于距锥尖0.20的相对位置，进气道处于超临界工作状态。发动机在此工作状态下，先使进气道出口压力按燃油调节的额定速率爬升；当流场探测装置判断出激波越过流场探测装置后，进气道出口压力按额定速率下降。

图10和图11给出了进气道出口压力变化曲线、进气道内流场探测装置处的压力变化曲线。由计算结果可以看出，发动机进气道出口压力先爬升，当流场探测装置判断出激波越过流场探测装置后，进气道出口压力下降，减小幅度为当前压力的3%，进气道出口压力变化曲线见图10。从图11可知，进气道结尾激波在0.055 s后越过流场探测装置，控制系统捕捉到激波越过流场探测装置后，进气道出口压力开始降低，激波位置继续前移至距进气道锥尖相对位置0.186处，0.215 s后激波回到安全位置，从判断激波越过流场探测装置到控制激波回到安全位置的时间为0.165 s。由流场探测装置处的压力变化可以看出，激波越过流场探测装置后，该处压力有一个突然跃升，之后，由于背压开始降低，此处压力也开始逐渐降低，直到激波退回时越过此点，此处压力有突然下降。

当流场探测装置监测到激波进入危险区后，燃烧室供油流量如果采用加速电磁阀快速调节迅速下降，减小幅度为当前压力的3%，则整个激波位置的控制时间减小到0.05 s，见图12和图13。

上述仿真计算中，进气道出口压力爬升规律均是以PWM电磁阀的额定调节能力进行确定的。如果导弹或飞行器的机动推力需要快速增大，此时需要开启加速电磁阀，大速率增加燃油流量，当激波越过流场探测装置边界时，燃油流量以额定速率的减小，进气道出口压力下降幅度为原压力的3%，4%，5%及6%，如图14所示。

图15给出了流场探测装置处的压力曲线，图16给出了激波位置曲线，从中可以看出，当发动机燃油流量快速增大、进气道出口压力迅速跃升时，进气道结尾激波位置前移速度加快，0.02 s后激波越过流场探测装置，前移至约0.175的相对位置。此时，进气道的出口压力开始降低，如果降低的幅度较小(3%和4%)，激波位置往后端运动一段距离(相对位置0.180，0.187)，但并不能使激波重新回到流场探测装置后的安全位置。只有进气道出口压力降低到一定的幅度之后(5%)，进气道的结尾激波才能回到安全的位置。出现上述现象的主要原因是进气道结尾激波向后越过探测元件回到安全位置的压力(0.786 MPa)要远低于激波向前越过探测元件的压力(0.827 MPa)，激波前后运动存在压力迟滞环现象。

前个算例在计算时没有考虑发动机燃油供应控制调节系统的延迟时间，根据试验结果取该时间为0.1 s。考虑延迟时间后，进气道出口压力跃升仍按加速电磁阀快速调节速率调节，压力下降仍以燃油流量额定速率减小，仿真结果见图17和图18。可以看出，当进气道出口压力上升至0.854 MPa时越过流场探测装置，此时进气道出口压力仍持续上升，在0.05 s时升至最大0.863 MPa，此时激波位置也前传至距锥尖相对位置0.132，约0.1 s时进气道出口压力开始下降，但激波并没有马上后移，而是到0.14 s时才开始后移，当进气道出口压力降低到当前进气道出口压力的9%(即0.79 MPa)及以上时激波才再次越过流场探测装置回到安全位置。可以看出，发动机燃油系统的延迟作用使激波前后运动存在压力滞环现象更为明显。

上述仿真计算了当发动机燃油供应控制系统以额定、快速调节速率调节燃油流量进气道出口压力爬升和下降时，进气道内结尾激波的响应情况，可以看出：

使用PWM电磁阀额定调节燃油流量与使用加速电磁阀快速调节燃油流量相比，进气道出口压力爬升时间常数从0.055 s降为0.02 s，激波越过喘振边界耗时从0.05 s降为0.025 s，进气道结尾激波向唇口方向运动的相对位移从0.186降为0.175，进气道出口压力的最大值从0.814 MPa升至0.827 MPa，使激波控制回安全区域，进气道出口压力需要更大的降低幅值(从3%增至5%)，然而当激波控制回到喘振边界范围的安全区域后，进气道出口压力的绝对值基本一致，约为0.79 MPa。

当考虑发动机燃油供应控制系统的延迟时间后，进气道出口压力升至更高的0.854 MPa，结尾激波越过喘振保护边界后进一步往危险方向运动，结尾激波的相对位移从0.175移至0.132，此时需要大幅降低当前进气道出口压力值(9%)，直到进气道出口压力值达到约0.79 MPa时，激波才控制回到喘振保护边界范围内。

3 结论

本文提出了一种快速确定流场探测装置安装位置及确定激波控制策略的方法，基于该方法对某型号冲压发动机的流场探测装置的喘振控制过程进行了仿真研究，得出以下结论：

1)在一维变截面流动控制方程中增加摩擦阻力项可以较为准确的确定进气道的结尾激波位置。据此在某型号发动机设计工作高度和马赫数下的临界喘振裕度时，给出了流场探测装置的安装位置，也即发动机的喘振保护边界，位于距进气道锥尖相对位置0.192处。

2)当发动机燃烧室压力阶跃变化时，进气道喉道下游结尾激波前压力响应时间较短，而发动机的实际供油调节特性较慢，进气道内压力波传播时间相对于燃油调节时间基本可以忽略。

3)由于进气道内激波前后运动存在明显的压力滞环现象，当激波越过喘振边界时，进气道出口压力会进一步上升，发动机喘振危险加大，此时应使用加速电磁阀快速减小燃油流量使进气道出口压力降低， 可以快速控制激波回到喘振边界范围的安全区域。

[1] TRAPIERSimon， DECK Sébastien， DUVEAU Philippe， et al. Time-frequency analysis and detection of supersonic inlet buzz [J]. AIAA journal， 2007 45(9)： 7-13.

[2] STERBENTZ W， EVVARD J. Criterions for prediction and control of ramjet flow pulsations：NACA RM E51C27 [R]. USA： NACA， 1951.

[3] NEWSOME R. Numerical simulation of near-critical and unsteady， subcritical inlet flow [J]. AIAA journal， 1984， 22(10)： 1375-1379.

[4] LU P J， JAIN L T. Numerical investigation of inlet buzz flow [J]. Journal of propulsion and power， 1998， 14(1)： 90-100.

[5] TRAPIER S， DECK S， DUVEAU P， et al. Delayed detached-eddy simulation of supersonic inlet buzz： AIAA 2007-4353 [R]. USA： AIAA， 2007.

[6] FERRI A， NUCCI L M. The origin of aerodynamic instability of supersonic inlets at subcritical conditions： NACA RM L50K30 [R]. USA： NACA， 1951.

[7] DAILEY C L. Supersonic diffuser instability [D]. Pasadena， CA： California Inst. of Technology， 1954.

[8] TRIMPI R. A Theory for stability and buzz pulsation amplitude in ramjets and an experimental investigation including scale effects [R]. USA： NACA Rept， 1956.

[9] FISHER S A， NEALE M C， BROOKS A J. On the sub-critical stability of variable ramp intakes at Mach numbers around 2： ARC-R/M-3711 [R]. England： National Gas Turbine Establishment， 1970.

[10] NAGASHIMA T， OBOKATA T， ASANUMA T. Experiment of supersonic air intake buzz [R] Tokyo： Institute of Space and Aeronautical Science， 1972.

[11] HONGPRAPAS Sorarat， KOZAK J D， MOSES Brooks， et al. A small scale experiment for investigating the stability of a supersonic inlet [J]. AIAA journal， 1997， 27： 1031-1037

[12] 孙健国，黄金泉. 发动机喘振裕度自适应控制[J]. 航空动力学报. 1993.7(3)： 279-282.

[13] 何中伟，张世英. 轴对称超音速进气道喘振及其控制[J]. 航空学报. 1983(2)： 73-82.

[14] OHSHIMA Takao， KANBE Katsuhiro. Control of the intake shock-position in the test rig for ramjet engine： AIAA 1977-2885 [R]. USA： AIAA， 1977.

[15] STERBENTZ W H.， EVVARD J C. Criterions for prediction and control of ram-jet flow pulsations： NACA 3506 [R]. USA： NACA，1955.

[16] CROWL R， DUNBAR W R， WENTWORTH C. Experimental investigation of marquard shock-positioning control unit on a 28-inch ramjet engine： NACA RM E56E09 [R]. USA： NACA，1967.

[17] HURRELLH G， VASU George， DUNBAR W R. Experimental study of shock-positioning method of ram-jet-engine control： NACA RM E55F21 [R]. USA： NACA， 1955.

Simulation research on ramjet buzz control based on flow field detecting technology

LIANG Junlong1， WANG Yufeng2， ZHANG Guitian1

(1. State Key Laboratory of Combustion， Thermal Structure and Inner Flow Field， School of Astronautics， Northwestern Polytechnical University， Xi’an 710072，China； 2. Xi’an Aerospace Propulsion Institute， Xi’an 710100，China)

In order to make the ramjet performance optimization and always work in a security state， the ramjet’s buzz margin should be keep in minimum and within the buzz boundary. A flow field detecting device that can distinguish the supersonic or subsonic flow field status is installed in the buzz boundary to control shock wave location at the intake terminal. Aiming at the one-dimensional variable cross-section flow control equations， the installation position of the flow field detecting device and the fuel reduction law of the control system after the shock wave goes through flow field detecting device are studied in this paper. The simulation result indicates that the method to use the test data to correct theoretical simulation data can accurately catch the shock wave at intake terminal， and according to the critical buzz margin designed for a certain type ramjet， can determine the installation location of the shock exploring device. The pressure along intake changes with the variation of engine’s fuel flow， pressure wave propagation time relative to the fuel regulating time can be ignored. As the existence of the pressure hysteresis phenomenon is obvious before and after the intake shock motion， when the shock goes through the buzz boundary， the pressure at intake exit will rise further， the engine buzz risk increases， and the acceleration electromagnetic valve should be adopted to quickly reduce fuel flow， so as to make the shock wave go back to a safe area.

ramjet；shock wave detection；buzz control；simulation

2016-12-28；

2017-03-19

共用技术基础研究项目(304030202)

梁俊龙(1977—)，男，博士，研究领域为航空宇航推进理论与工程

V235.213-34

A

1672-9374(2017)06-0061-09

(编辑：马 杰)