基于相关算法的PSK信号载频和码速率估计方法研究

王琦琦，董春曦

(西安电子科技大学，陕西 西安 710071)

基于相关算法的PSK信号载频和码速率估计方法研究

王琦琦，董春曦

(西安电子科技大学，陕西 西安 710071)

针对估计相移键控(PSK)信号的码速率时需要构建多维矩阵从而导致计算复杂度高的问题，提出首先使用循环自相关的一维切片估计信号载频，然后根据载频的估计值构造相关接收机，使用相关接收机得到码元宽度的粗估计结果后，以此作为循环自相关计算的延迟值并以此缩小循环频率计算区间，从而得到码速率的精确估计结果。此方法的运算复杂度低，操作简单，能够获得载频及码速率的精确估计结果，且适用于低信噪比的情况。分析了此方法的运算复杂度，并通过仿真实验对该估计方法进行了验证，实验结果证实了方法的有效性。

循环自相关；相关接收机；码速率

1 研究背景

在电子对抗领域，只有准确地获取信号的调制参数才能更加有效地实施干扰，信号参数的估计因此具有非常重要的作用。然而，由于侦察方完全未知信号的各种信息，需要对大量数据进行各种变换才能得到参数的估计，这造成了很大的困难。此外，对于侦察方来说，截获的信号往往具有比较低的信噪比，使得估计算法必须具有很好的抑制噪声的能力。

早在1948年，Ville把Wigner提出的分布方法应用于信号分析领域后，Wigner-Ville分布(WVD)在非平稳信号分析中占据重要地位。调制信号作为非平稳信号可以使用Wigner-Ville分布有效地得到其能量分布情况，与传统的傅里叶变换相比有很大的优越性。直到Gardner等人提出循环平稳理论后，一种基于循环平稳的循环谱估计方法被广泛研究并在许多领域得到应用。Gardner本人在文献[1]和[2]中分别介绍了循环谱相关的方法在模拟调制以及数字调制信号中的应用。

2 研究现状

循环谱估计的方法对噪声的抑制性很好，可以有效地估计信号的参数，并且具有广泛的用途。但是，循环密度谱的方法属于三维计算，计算复杂度高，需要进行2次傅里叶变换的计算，不易于理解和实现。在循环密度谱方法的基础上，文献[3]提出了基于循环自相关统计量，运用一维切片搜索的方法进行载频以及码速率的估计，大大减少了计算量，但是由于无法确定合适的延迟时间，需要计算1组时间延迟下的循环自相关结果，难以实际应用。文献[4]提出使用相关接收机的方法进行码速率的估计，这种方法的计算复杂度低，适合快速处理，但是要事先知道信号的载频，且估计精度不高。本文针对2种方法中的缺点，结合使用2种方法，使用循环自相关估计信号的载频，然后构造相关接收机法进行码速率的粗估计，使用粗估计结果获得合适的延迟时间，得到码速率的精确估计。

3 理论依据

3.1 循环自相关的理论基础

设x(t)为一离散循环平稳随机过程，其时变相关函数定义为[5]：

Rx(t;τ)=E{x(t)x*(t-τ)}

(1)

则x(t)的循环自相关函数定义为：

(2)

式中：α为循环频率；τ为延迟时间。

对于二进制相移键控(BPSK)信号，可建模为：

(3)

式中：q(t)为调制脉冲；Tc为码元宽度；f0为信号载频；θn为相位信息，且等概率取值0和π；t0为信号起始时刻；φ0为信号初相。

由此可得，BPSK信号的循环自相关函数为：

(4)

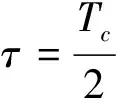
3.2 相关接收机的理论基础

对于含有噪声的BPSK信号，表示为：

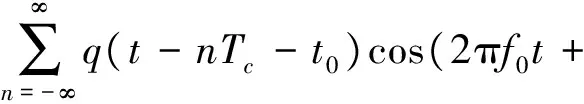
θn+φ0)+n(t)

(5)

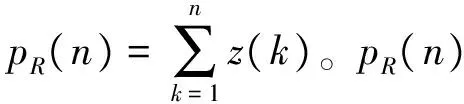
4 优化的载频和码速率估计方法

4.1 载频和码速率估计方法

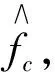
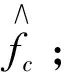
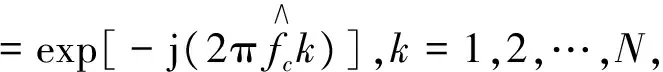
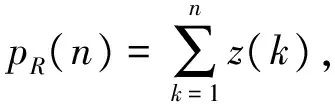
(4) 搜索pR(n)拐点位置，得到数列p(i)(i=1,2,…l)，其中l为拐点的个数，根据p(i)获得每个拐点之间的间隔N(j)=[p(i+1)-p(i)](j=1,2,…，l-1)，N(j)表示2个拐点之间的采样点数，也就是每次相位跳变之间的采样点数。假设每个码元宽度内的采样点数为Nd，则N(j)=kNd,k∈N；

(5) 选取N(j)的最小值作为1个码元中所包含的采样点数的估计值，得到循环自相关计算的延迟间隔τn=min{N(j),j=1,2,…，l-1}/2；

(6) 计算信号s(k)在延迟时间τn、循环频率[-2fs/Nd,2fs/Nd]下的循环自相关函数，搜索距离零频最近的峰值位置，得到码速率的精确估计结果。

4.2 计算量分析

对于样本总数为N的样本，在固定延迟下，对于每个循环频率，一次循环自相关计算的乘法次数为N次，加法次数为N-1次。如果使用文献[3]中所提到的方法，延迟时间取1组长度为Nτ的数组，则对于Nα个循环频率点的信号的循环自相关函数需要计算的次数为(2N-1)·Nτ·Nα。对于相关接收机的计算，需要进行N次乘法以及N-1次加法来获得拐点曲线pR(n)，以及O(N)次数量级的计算来获得拐点间隔。因此，使用本文所提的方法，若Nd为使用相关接收机估计所得每个码元内的采样点数，延迟时间取估计所得的固定值Nd/2，循环频率计算区间为[-2fs/Nd,2fs/Nd]，则循环自相关进行码速率估计的计算减少为(2N-1)·4Nd+O(N)。对于采样点数8 000点，循环频率4 000点的BPSK信号来说，如果延迟数组取为100组，1个码元宽度内的采样点数为50点，则文献[3]中的方法计算量为6.399 6×109，而本文所提方法的计算量为3.207 8×106，计算量减少了一半，如果采样点数越多，改善量越明显。

5 仿真验证

仿真采样频率fs=4 000 Hz，载频fc=650 Hz，码元速率fd=100 Hz，信噪比为=0 dB的BPSK信号，采样数据点数为8 000点。

计算延迟时间τ=0时的循环自相关函数Rs(α;0)，结果如图1所示。

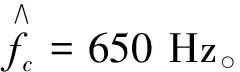
构建相关接收机，使信号通过相关接收机后得到结果pR(n)以及为消除毛刺的影响平滑滤波后的结果，如图2、图3所示。

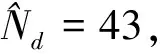
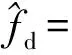
6 结束语

本文提出了一种将循环自相关码速率精确估计以及相关接收机码速率粗估计相结合的新方法，弥补了2种方法各自的缺点，在计算量大大减少的情况下也能够非常准确地估计信号码速率。此外，构建相关接收机时所需要的载频值的先验知识也可以使用循环自相关的方法在τ=0的延迟时间下获得非常准确的估计值，这样就不需要引入第3种算法。由于循环自相关以及相关接收机2种方法都是基于相关计算的，对于噪声有很好的抑制效果，所以将2种算法结合后在比较低的信噪比下仍可准确地估计载频和码速率。

[1] GARDNER W A.Spectral correlation of modulated signals:PartⅠ-analog modulation[J].IEEE Transactions on Communication,1987,35(6):584-594.

[2] GARDNER W A ,BROWN W A,CHEN C.Spectral correlation of modulated signals:PartⅡ-digital modulation[J].IEEE Transactions on Communication,1987,35(6):595-601.

[3] 金艳，姬红兵.基于循环自相关的PSK信号盲参数估计新方法[J].西安电子科技大学学报(自然科学版)，2006,33(6):892-896.

[4] 邓振淼，刘渝，梁帅.PSK伪码速率估计[J].南京航空航天大学学报，2006,38(1):91-95.

[5] 张贤达，保铮.非平稳信号分析[M].3版.北京：国防工业出版社，1998.

ResearchintoEstimationMethodofCarrierFrequencyandCodeRateforPSKSignalsBasedonRelatedAlgorithms

WANG Qi-qi,DONG Chun-xi

(Xidian University，Xi'an 710071，China)

The calculation complexity is high due to multi-dimension matrix construction when the code rate of phase-shift keying (PSK) signals is estimated,so this paper presents a method,which firstly uses one-dimension slice of the cyclic autocorrelation for signal to estimate the carrier frequency of signals,then a correlation receiver is obtained according to the estimated parameters of carrier frequency.After the code rate is estimated roughly by using the correlation receiver，the rate is taken as the delay value of the cyclic autocorrelation and the interval of the cycle frequency can be lessened,thereby the accurate estimation of the code rate can be obtained.The complication of this method is low,and the method is simple in operation,accurate in estimation and effective for situations of low signal to noise ratio (SNR).This paper analyzes the computation complexity of this method,validates the estimation method through simulation experiment,and the experiment result verifies the effectiveness of this method.

cyclic autocorrelation;correlation receiver;code rate

2017-03-17

TN971.1

A

CN32-1413(2017)06-0083-04

10.16426/j.cnki.jcdzdk.2017.06.018