一种基于相关数据段自适应可变长的频偏估计方法
2018-01-11黄子甲
黄子甲
(西安导航技术研究所,陕西 西安 710068)
一种基于相关数据段自适应可变长的频偏估计方法
黄子甲
(西安导航技术研究所,陕西 西安 710068)
为了克服现有技术的不足,提出了基于频率范围受限的自适应可变长的频偏估计方法。即利用随机变化的信噪比,得到自适应的自相关特殊数据段的长度,并通过限制频偏估计范围,进而降低特殊数据段的自相关运算复杂度,实现在自相关运算复杂度得到控制的条件下自适应信噪比的变化,提高频偏估计的抗噪性和精度。
频偏估计;自相关数据段;信噪比
0 引 言
为了在宽带数字接收机系统中消除由于多普勒效应和收发端晶振不一致等因素引起的频偏,基于频率范围受限的频偏估计技术[1-2]被提出。接收信号中特殊的数据段的相关值是很容易检测到的,该值包含着频偏值,避免了因为需要调整本地特殊序列而不得不额外增加载波同步和相位同步算法,提高了同步效率。
当前基于频率范围受限的频偏估计方法主要关注于在特殊数据段的固定长度条件下的自相关运算[3]。这些方案对于信噪比随机变化和需要较低的自相关运算复杂度的环境是很难执行的。对于已有的可以实现控制自相关运算复杂度的基于频率范围受限的频率估计方法[4],虽然可以通过调节相关数据段的长度控制自相关的运算复杂度,但是这些方法不能自适应控制和调节相关数据段的长度,而且忽略了由于缩短相关数据段的长度而导致的抗噪性能的下降,以及由于过度扩展相关长度所引起的频偏估计范围的缩小,这些缺点都会直接影响频偏估计的准确性。
本文分析了相邻2段数据做频偏估计相关时信噪比与相关数据段长度的关系,并提出一种相关数据段长度根据信噪比自适应变化的频偏估计算法,实现在自相关运算复杂度得到控制的条件下自适应信噪比的变化。
1 系统模型
利用同步头完成数据帧的捕获,在捕获的基础上利用训练序列进行可变长相关数据段长度的频偏估计和校正。
传统的频偏估计结构如图1所示,无噪声情况下,收端的基带信号模型为s(n)=AejωΔn,其中wΔ为频偏,A为信号幅度,设相关距离为K,则该信号模型的自相关函数可以表示为:

|A|2ejωΔK
(1)
可以看到,相位中包含了信号的频率信息。因而频偏的估计值为:
(2)
由于Frank序列优秀的自相关性质,频偏估计使用Frank序列作为训练序列。
2 信噪比与相关距离的长度关系
时域自相关频率估计算法的性能主要受自相关函数估计中所产生误差的影响。文献[4]、[5]给出了信噪比与相关距离的长度关系,其频偏估计误差的均方差为:

(3)
这就是传统算法中信噪比γ、相关距离K、频偏估计数据长度N-K和相位误差的均方差var[δω]的关系式。频偏估计误差的均方差var[δω]反映了频偏估计的准确性。
但是这种关系需要进一步扩展到具体的频偏估计的相关数据结构中。
以下进行相邻两数据段频偏估计的相关运算。考虑一种经常用到的场景,即采用相邻2段数据做频偏估计相关运算,于是K-1=N-K,所以min(N-K,K)=N-K,于是:
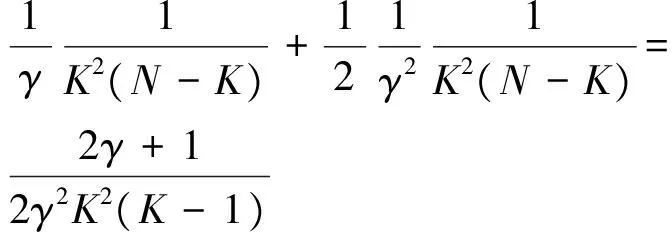
(4)
可得:
(5)
这就是当采用相邻2段数据做频偏估计相关运算时,信噪比γ与相关距离K的关系。但是这种解的形式不便于分析,于是对式(5)变形得:
(6)
当var[δω]固定,相关距离K变大时,需要的信噪比减小。由于是采用相邻2段数据做频偏估计相关运算,相关距离K变大时,相关数据段长度也要变大。
进一步,由于相关数据段长度为K-1=N-K,所以信噪比与相关数据段长度的关系为:
(7)
式(6)、(7)本质上是一致的。采用相邻2段数据做频偏估计相关运算,当var[δω]固定时,若相关距离K或相关数据段长度变大,均可降低对信噪比的要求。
由结论可知:对于相邻数据段时域相关频偏估计,相关距离或者相关数据段越短,频偏估计越不准。
3 建议算法
可以根据式(7),令L′=N-K,因为L′≫1,可得:
(8)
可以根据相关数据段长度L′与信噪比γ的关系,根据信噪比自适应调节所需相关数据段的长度,再进行频偏估计,具体算法如下:
步骤1:根据系统中存在频偏的上限fΔ_max得到参与相关数据长度L的最大值Lmax,即:
(9)

步骤3:构建相邻2段含有若干个Frank序列的数据结构作为频偏估计数据段。即每一段数据结构均含有N个连续的Frank序列,二者结构和数据完全一致,长度均为NM。数据结构如下:[F1,F2,…,Fi,…,FN,F1,F2,…,Fi,…,FN],其中Fi代表第i个Frank序列,令相关距离K=NM+1。
步骤4:系统根据信噪比调节参与相关的数据段的长短,即利用式(8)调节。

步骤6:相关运算得到频偏估计值。
4 仿真与分析
系统采用OQPSK调制,信息速率120 Mbps,采样速率120 MHz,滚降系数0.2,仿真统计结果为 100 000次独立运行所得到的误比特率的平均值,Frank序列长度为分别取L=64,128,256,信噪比在-5~25 dB 之间。频偏估计序列的总长度为2 046 bit,包含2个1 024 bit的自相关段,对应于64、128、256,每个自相关段包含的Frank序列个数分别为16,8,4。对比算法采用传统算法,即直接用2段1 024 bit的Frank数据做自相关,进行频偏估计。
由图2可得,由于传统算法始终采用全部的Frank序列,并没有选择部分Frank序列进行自相关频偏估计,所以性能保持最好。建议算法L=64的曲线与传统算法的曲线非常接近,说明建议算法L=64的不仅有着趋近于传统算法的性能,而且可以随着信噪比的增加而灵活选择合适的Frank的个数。L=64是Frank的最小长度,提供了较多的灵活性;而建议算法L=128和建议算法L=256,相对于L=64,由于Frank过于长,使得在根据信噪比选择相关数据段长度时,不得不为了得到整数个Frank序列而失去频偏估计的精确性,丧失了灵活性。所以建议算法L=128和建议算法L=256的性能均低于建议算法L=64。
5 结束语
针对传统频偏估计算法中相关数据段长度在高信噪比下固定不变的缺点,本文分析了相邻2段数据做频偏估计相关时,信噪比与相关数据段长度的关系,并提出了频偏估计误差随相关距离的增大而急剧减小,频偏估计进而精准等结论,然后提出一种相关数据段长度根据信噪比自适应变化的频偏估计算法,最后通过仿真证明了建议算法的有效性。
[1] FITZ M.Futher results in the fast estimation of a single frequency[J].IEEE Transactions on Communication,1994,42(2-4):862-864.
[2] ANDREAN A,MENGALI U,REGGIANNINI R.The modified Cramer-Rao bound and its applicaction to synchronization problems[J].IEEE Transactions on Communication,1994,3(6):1391-1399.
[3] LANK G,REED I,POLLON G.A semicoherent detection and Doppler estimation statistic [J].IEEE Transactions on Aerospace Electronic System,1973,9(2):151-165.
[4] 杨萃.噪声环境下频率估计算法研究[D].广州:华南理工大学,2010.
[5] HANDEL P,ERIKSSON A,WIGREN T.Performance analysis of a correlation based single tone frequency estimation [J].Signal Processing,1995(5):223-231.
AFrequencyOffsetEstimationMethodBasedonAdaptiveVariable-lengthofCorrelativeDataSegment
HUANG Zi-jia
(Xi'an Research Institute of Navigation Technology,Xi'an 710068,China)
In order to overcome the shortcomings of existing technologies,this paper puts forward an adaptive variable-length frequency offset estimation method based on frequency range limitation,which uses the randomized signal to noise ratio to obtain the length of adaptive autocorrelation special data segment,and reduces the autocorrelation operation complexity of special data segment by limiting the frequency offset estimation range,realizes the change of adaptive signal to noise ratio under the conditions that the autocorrelation operation complexity is controlled,improves the anti-noise performance and accuracy of frequency offset estimation.
frequency offset estimation;autocorrelation data segment;signal to noise ratio
2017-05-09
TN821
A
CN32-1413(2017)06-0072-03
10.16426/j.cnki.jcdzdk.2017.06.015
