环境参数对L波段盐度计观测亮温的影响研究

王迎强 ，严 明 ，严 卫 ，张 锐 ，李 萍

（1．国防科技大学 气象海洋学院，江苏 南京211101;2．中国航海图书出版社，天津 300450；3．94755部队，福建 漳州 363000，4．陆军工程大学，江苏 南京 211101）

海表面盐度是海洋-气候系统中最重要的参数之一，在大洋环流、海气相互作用等全球大气、海洋过程中起着重要的作用，是认识海洋、揭示海洋现象必不可少的要素。传统手段对海表面盐度的观测主要依靠船舶、浮标以及固定平台等方式实现，覆盖面相对较小，观测周期不稳定，所获得的海表面盐度数据不能满足科学研究的需要。航空遥感虽然机动性较强，分辨率较高，但费用较为昂贵，不适宜进行大范围长时间观测。星载海洋盐度计依据海表面盐度在微波波段的辐射特性，通过构建海面微波辐射探测器，利用海面辐射亮温、海表面粗糙度以及海面温度等信息反演得到海表面盐度，是实现全球海洋盐度观测的有效手段。

随着获取全球高精度海表盐度数据的迫切需求，除了已经在轨运行的ESA的SMOS卫星以及NASA的Aquarius卫星以外，还有ESA计划实施的SMOSSops卫星和SMOSops-H卫星，我国的“海洋盐度探测卫星”工程也已步上正轨。从目前在轨运行的盐度卫星情况来看，两颗卫星的盐度测量精度均未达到设计指标，这与未采用校正温度的同步测量手段、RFI污染、系统长时间漂移、物理模型的合理性、环境参数等因素有关[1]。本文在构建L波段盐度计正演模型的基础上，利用敏感性分析方法研究海洋大气空间环境参数对盐度计观测亮温的影响，从而为提高海表盐度反演精度提供一定的理论依据。

1 L波段辐射正演模型

对于星载盐度计而言，它所接收到的辐射亮温来源包括海面辐射的亮温Tbsea、大气上行辐射亮温Tbup、大气下行辐射亮温Tbdown以及海面反射的宇宙背景辐射亮温Tbcos。从而，盐度计接收到的总的辐射亮温TbAF可以表示为[2]:

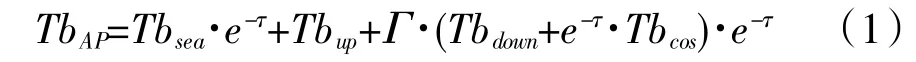
式中：τ为大气光学厚度；Γ为海面反射率。

由式（1）可以看出，L波段辐射传输正演模型主要包括海面部分、大气部分、电离层部分以及宇宙辐射等部分，其中海面部又分为平静海面部分以及由海面风场引起的风生亮温部分两块内容。L波段辐射传输正演模型框架如图1所示，其输入量为海表面盐度、海面温度、入射角、海面风速、风向、大气水汽含量、海表大气温压、宇宙背景辐射、法拉第旋转角等，输出量为辐射计的各极化通道观测亮温。对于海表面盐度的反演而言主要使用了辐射计的垂直极化通道和水平极化通道亮温。

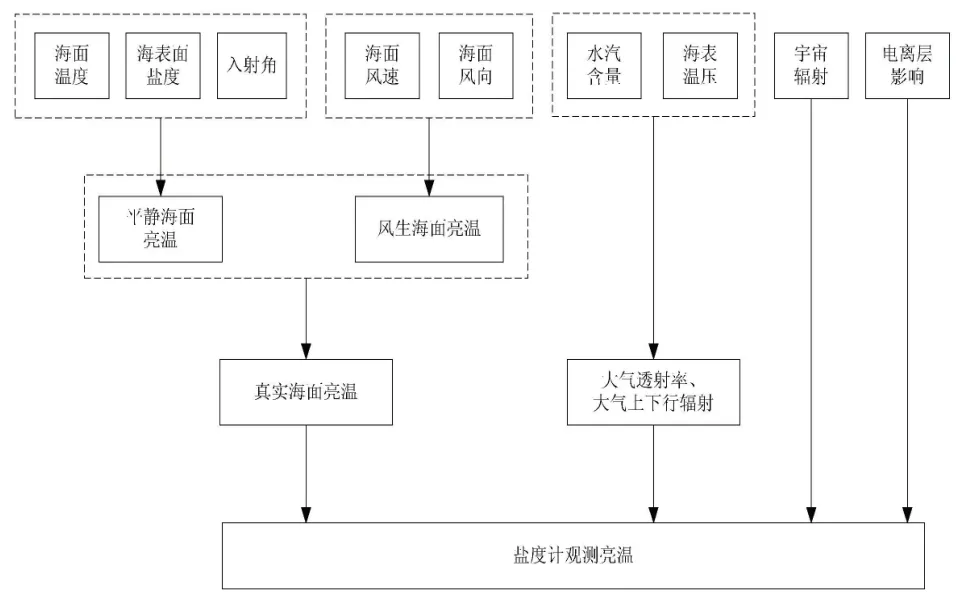
图1 L波段辐射传输正演框架图

平静海面亮温的计算需要用到海水介电常数模型，针对L波段的介电常数模型主要有Klern-Swift（KS）模型[3]、Messiner-Wentz（MW）模型[4]、Blanch模型[5]、GW模型[6]等，目前已经在轨的两颗盐度遥感卫星中，SMOS卫星在反演算法中使用KS模型，Aquarius卫星使用MW模型，本文选用的是在微波波段使用广泛的KS模型。

风生海面亮温的计算需要用到海面粗糙度模型，目前海面粗糙度模型主要有双尺度模型、小斜率模型以及经验模型等。SMOS卫星使用的海面粗糙度模型分别是双尺度模型[7]（使用修正的Durden&Vesecky海浪谱，并加入了海面泡沫模型）、小斜率模型[8]（使用Kudryatsev海浪谱）以及Gabarro′经验模型[9]，而Aquarius卫星由于其主被动结合的体制，海面粗糙度模型采用的则是基于实测数据得到一种经验关系模型[10]。双尺度加泡沫模型不仅考虑了海面风速和风向对海表亮温的影响，并且加入了由风引起海浪破碎产生的海面泡沫覆盖，具有较高的仿真能力[11]，本文使用该模型来计算风生海面亮温。

大气校正的计算主要是考虑大气氧气和水汽的吸收衰减作用。SMOS团队利用Zine等提出的经验化的L波段大气辐射传输模型用以替代需要基于Ulaby关于氧气和水汽衰减系数计算的多层模型[12-13]。Aquarius团队则是根据NCEP温压湿廓线数据，基于Liebe等的氧气吸收模型以及Rosenkranz的水汽吸收模型，结合大气辐射传输模型计算出大气辐射参数，从而进行大气校正[14-15]。为了计算方便，本文首先利用考虑了氧气和水汽吸收衰减的Zine经验模型，其次在研究降水的影响时，利用Liebe的MPM93传播模型进行仿真计算[16-17]。

电离层影响主要考虑到电磁波穿越电离层时的法拉第旋转效应，可表示为[18]：

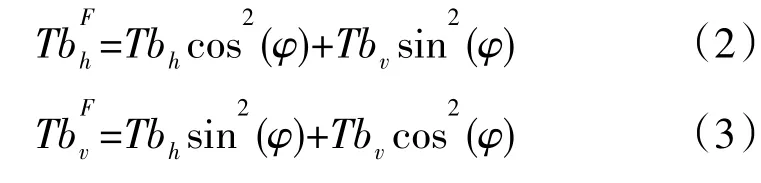
式中：TbFh和TbFv为经过法拉第旋转后的水平和垂直极化亮温；Tbh和Tbv为法拉第旋转前的水平和垂直极化亮温；φ为法拉第旋转角。

2 敏感性分析

敏感性分析是一种定量描述模型输入变量对输出变量的重要性程度的方法[19]。当模型的输入量发生一个微小变化时，输出量也会随之发生相应的变化，输出量的变化程度越大，则说明对该输入量的敏感性程度越高。敏感性程度的高低可以用敏感度系数来衡量。敏感度系数定义为：

式中：S为敏感度系数；ΔP为输入量的变化量；ΔT为输出量的变化量，本文中ΔP为正演模型中各参数的变化量，ΔT为辐射计观测亮温的变化量。

由图1可知，对L波段辐射传输正演模型的主要输入参数有海表面盐度、温度、入射角、海面风速、海面风向、海面气压、海表气温、大气水汽含量、法拉第旋转角以及降雨强度等。通过敏感性分析，可以得知辐射计观测亮温受这些输入参数的影响程度，从而确定辐射计在不同环境条件下对哪些参数较为敏感，哪些参数不敏感，为减小外界因素对海表面盐度反演精度的不利影响提供理论依据。

在进行敏感性分析前，首先要假设一个固定的背景场，然后在一合理范围内改变背景场中某一要素，通过仿真模型确定亮温随之发生的改变。假设背景场中的海表面盐度、温度、海表气温、风速、风向、海面气压、、大气水汽含量、降雨强度以及法拉第旋转角的变化范围如表1所示。

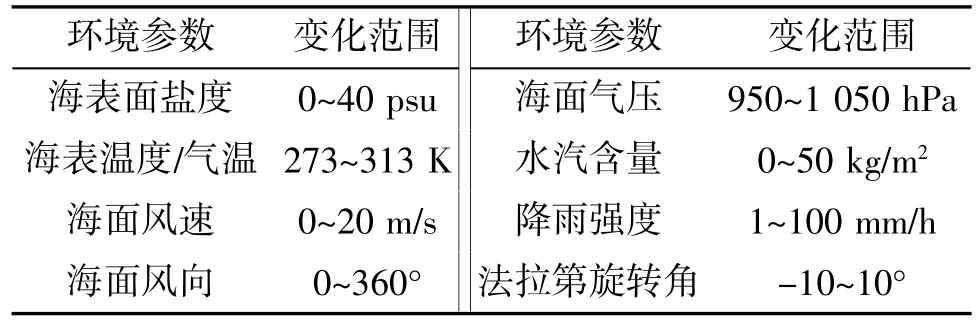
表1 主要环境影响要素的变化范围

2.1 海表面盐度的敏感性分析

假设海面风速为5 m/s，风向与辐射计观测方位角的相对夹角为0°，海表气温为288 K，海面气压为1 013 hPa，大气水汽含量为30 kg/m2，法拉第旋转角为0°。当辐射计入射角分别为10°、30°和50°时，敏感度系数在不同海面温度条件下随海表面盐度的变化情况如图2所示。

图2 亮温对海表面盐度的敏感度变化

从图2可以明显看出，辐射计观测亮温随海表面盐度敏感性在高盐度范围内的敏感性要整体优于低盐度范围内的敏感性，这说明辐射计的观测亮温在低盐环境下对海表面盐度较不敏感；海面温度越高，辐射计观测亮温随海表面盐度敏感性越强，这说明辐射计的观测亮温在低温环境下对海表面盐度较不敏感，而在高温环境下对海表面盐度较为敏感。

此外，入射角的变化会对亮温随盐度变化的敏感性产生一定影响。当入射角由10°增大到50°时，垂直极化通道亮温对海表面盐度的敏感性有所增加，而水平极化通道亮温在高盐度范围内对海表面盐度的敏感性有所减少，在低盐范围内敏感性有所加强。

2.2 海面温度的敏感性分析

假设海面风速为5 m/s，风向与辐射计观测方位角的相对夹角为0°，海表气温为288 K，海面气压为1 013 hPa，大气水汽含量为30 kg/m2，法拉第旋转角为 0°。当入射角分别为 10°、30°和 50°时，敏感度系数在不同海表面盐度条件下随海面温度的变化情况如图3所示。

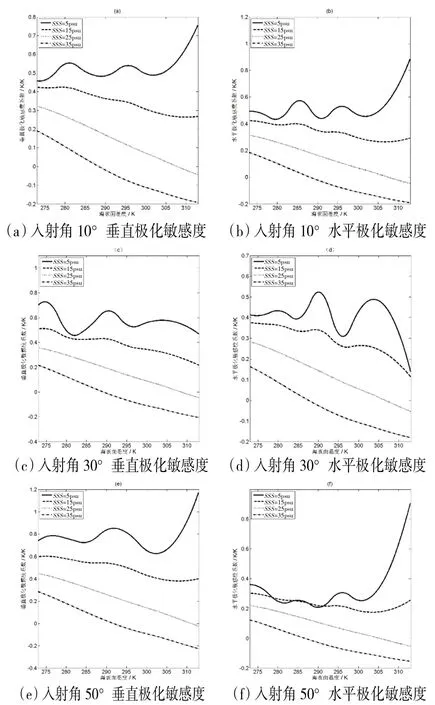
图3 亮温对海面温度的敏感度变化

从图3可以看出，随着海表面盐度的升高，垂直极化通道和水平极化通道亮温对海面温度的敏感性逐渐减少。在海表面盐度为35 psu的条件下，垂直极化通道亮温和水平极化通道亮温对海面温度的敏感度系数均约为-0．2 K/K～0．2 K/K。而在海表面盐度为5 psu的条件下，垂直极化通道亮温和水平极化通道亮温对海面温度的敏感性较高，其敏感度系数呈现波动变化，最高甚至可以达到1 K/K以上，这意味着1 K的温度误差将引起1 K以上的辐射计测温误差，严重影响到海表面盐度的反演精度。

当盐度为25 psu时，海面温度为30～40℃的范围内，垂直极化通道亮温和水平极化通道亮温的变化程度都很小，其敏感度系数接近等于零。而当盐度为35 psu时，敏感度系数较小。这说明在海表面盐度值处于通常情况下，辐射计观测亮温对海水温度较不敏感，因此在反演中海面温度误差对盐度反演精度的影响较小，但低温条件下海面温度误差对海表面盐度反演精度的影响不容忽视。

2.3 海面风场的敏感性分析

2．3．1 海面风速的敏感性分析 假设海表面盐度为35 psu，海面温度为290 K，海表气温为288 K，海面气压为1 013 hPa，大气水汽含量为30 kg/m2，风向与辐射计观测方位角的相对夹角为0°，法拉第旋转角为0°。那么当辐射计入射角分别为10°，30°，50°时，敏感度系数随海面风速的变化如图4所示。

图4 垂直和水平极化通道亮温对海面风速敏感度的变化

从图4可以看出，整体而言，垂直和水平极化通道敏感度系数都随着海面风速的增大而增大。在2～5 m/s的海面风速范围内，辐射计观测亮温对海面风速的敏感度系数较小，大约为0．1～0．3 K/（m/s）。当风速增大至20 m/s时，其敏感度系数可达1．5 K/（m/s），这主要是由于高风速条件下不仅对海面粗糙度大大增加，并且风浪破碎产生了泡沫覆盖，对海面亮温的贡献十分明显。此外，随着入射角的增大，垂直极化通道亮温对海面风速的敏感性逐渐下降。在风速为20 m/s入射角为50°的条件下，垂直极化通道亮温对海面风速的敏感度系数约为0．8 K/（m/s），而入射角为30°条件下的敏感度系数约为1．3 K/（m/s）。水平极化通道亮温在低风速段对风速的敏感性随着入射角的增大而增大，在风速大于13 m/s时也随这入射角的增大而减小。因此在高风速条件下，选择大入射角观测可以降低辐射计观测亮温对海面风速的敏感性，从而减小风速误差对海表面盐度反演精度的影响。

2．3．2 海面风向的敏感性分析 假设海表面盐度为35 psu，海面温度为290 K，海表气温为288 K，海面气压为1 013 hPa，大气水汽含量为30 kg/m2，海面风速为10 m/s，辐射计的观测方位角为0°，法拉第旋转角为0°。那么当辐射计入射角分别为10°，30°，50°时，敏感度系数随海面风向的变化如图5所示。

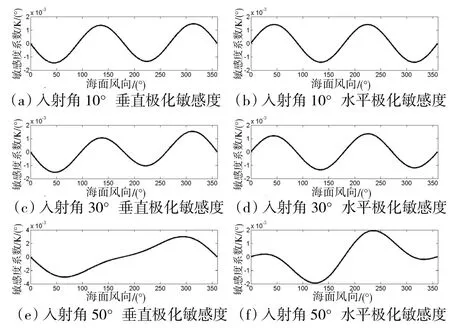
图5 亮温对海面风向敏感度的变化

从图5可以看出，随着海面风向的变化，垂直极化通道亮温和水平极化通道亮温敏感度系数呈现波动特征，在入射角为10°和30°的条件下，二者的波动方向恰好相反。总体而言，两个通道的敏感度系数十分微小，因此，风向的变化对辐射计观测亮温带来的影响要远小于风速变化的影响。

2.4 大气部分的敏感性分析

2．4．1 海表气温的敏感性分析 假设海表面盐度为35 psu，海面温度为290 K，海面气压为1 013 hPa，大气水汽含量为30 kg/m2，海面风速为5 m/s，风向与辐射计观测方位角的相对夹角为0°，法拉第旋转角为 0°。那么当辐射计入射角分别为 10°，30°，50°时，敏感度系数随海表气温的变化如图6所示。

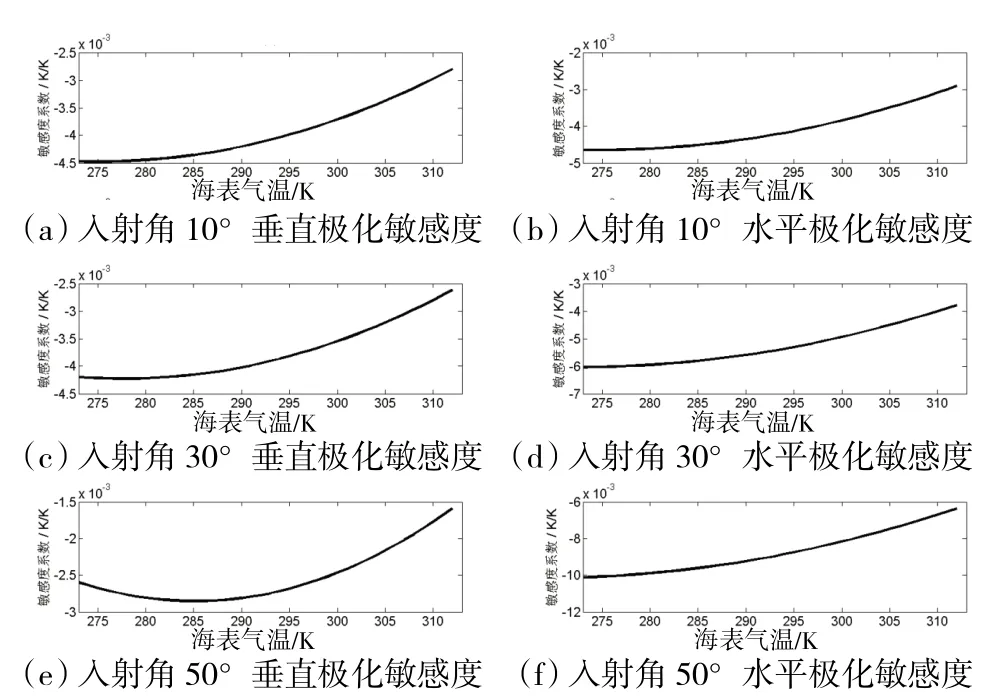
图6 亮温对海表气温敏感度的变化

由图6可以看出，垂直极化通道亮温对海表气温的敏感性都随着入射角的增大而减小，水平极化通道相反。尽管如此，两者的敏感度系数仍然较低，垂直极化通道敏感度系数在小入射角时约为-0．004 5～-0．025 K/K，水平极化通道的敏感度系数约为-0．006～-0．01 K/K。目前海表气温资料的精度可达2 K[20]，所引起的亮温变化不超过0．02 K，因此海表气温误差对盐度反演精度造成的影响很小。

2．4．2 海面气压的敏感性分析 假设海表面盐度为35 psu，海面温度为290 K，海表气温为288 K，大气水汽含量为30 kg/m2，海面风速为5 m/s，风向与辐射计观测方位角的相对夹角为0°，法拉第旋转角为 0°。那么当辐射计入射角分别为 10°，30°，50°时，敏感度系数随海面气压的变化如图7所示。

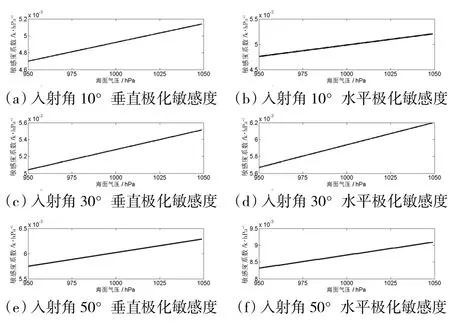
图7 亮温对海表气温敏感度的变化

从图7可以看出，垂直极化通道和水平极化通道的亮温敏感性都随着海面气压的升高而升高，且两者都随着入射角的增大而增大，尽管如此，垂直极化通道和水平极化通道的亮温对海面气压的敏感度系数大约为 0．004 7～0．009 K/hPa，目前海面气压资料的精度可达10 hPa[20]，所引起的亮温观测误差不超过0．1 K，因此海面气压误差对盐度反演精度的影响较小。

2．4．3 水汽含量的敏感性分析 假设海表面盐度为35 psu，海面温度为290 K，海表气温为288 K，海面气压为1 013 hPa，海面风速为5 m/s，风向与辐射计观测方位角的相对夹角为0°，法拉第旋转角为0°。那么当辐射计入射角分别为 10°，30°，50°时，敏感度系数随水汽含量的变化，如图8所示。

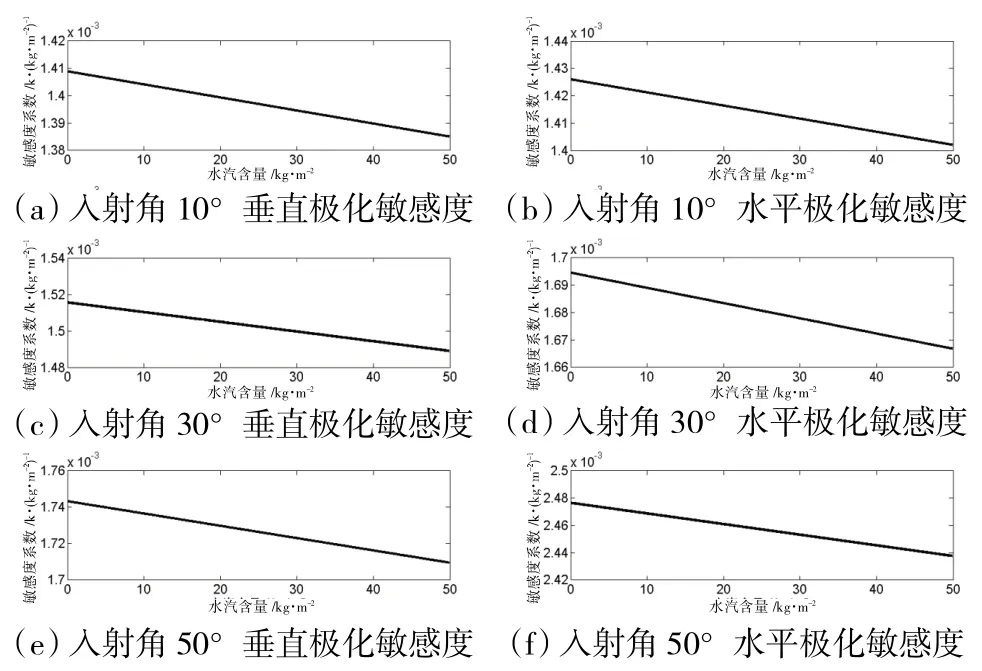
图8 亮温对水汽含量敏感度的变化

由图8可以看出，垂直极化通道和水平极化通道亮温敏感性系数都随着水汽含量的升高而减小，随入射角的增大而增大。垂直极化通道亮温对水汽含量的敏感度系数的变化范围约为0．001 38～0．001 74 K/（kg/m2），水平极化通道亮温对水汽含量的敏感度系数变化范围约为0．001 4～0．002 48 K/（kg/m2）。

2．4．4 降雨的敏感性分析 为了计算有降雨时的敏感度系数，首先需要利用MPM93毫米波传播模型计算有降雨时的大气衰减系数，其次根据微波辐射传输方程计算出垂直和水平极化亮温。这里假设降雨云的云底高为1．3 km，云顶高为2 km，云内液态水含量为 1．5 g/m3，地面水汽密度为 7．7 g/m3，海表面盐度为35 psu，海面温度为290 K，海表气温为288 K，海面气压为1 013 hPa，海面风速为5 m/s，风向与辐射计观测方位角的相对夹角为0°，法拉第旋转角为0°，那么当辐射计入射角分别为10°，30°，50°时，敏感度系数随降雨强度的变化如图9所示。

由图9可以看出，垂直极化通道和水平极化通道亮温敏感性系数都随着降雨强度的升高而减小，随入射角的增大而增大。垂直极化通道亮温对降雨强度的敏感度系数比水平极化通道小，分别在0．031 6～0．081 6 K/(mm/h)、0．031 9～0．105 4 K/(mm/h)，现有翻斗雨量计的降雨强度测量误差为0．1mm/h，因此降雨强度误差对盐度反演精度的影响较小。

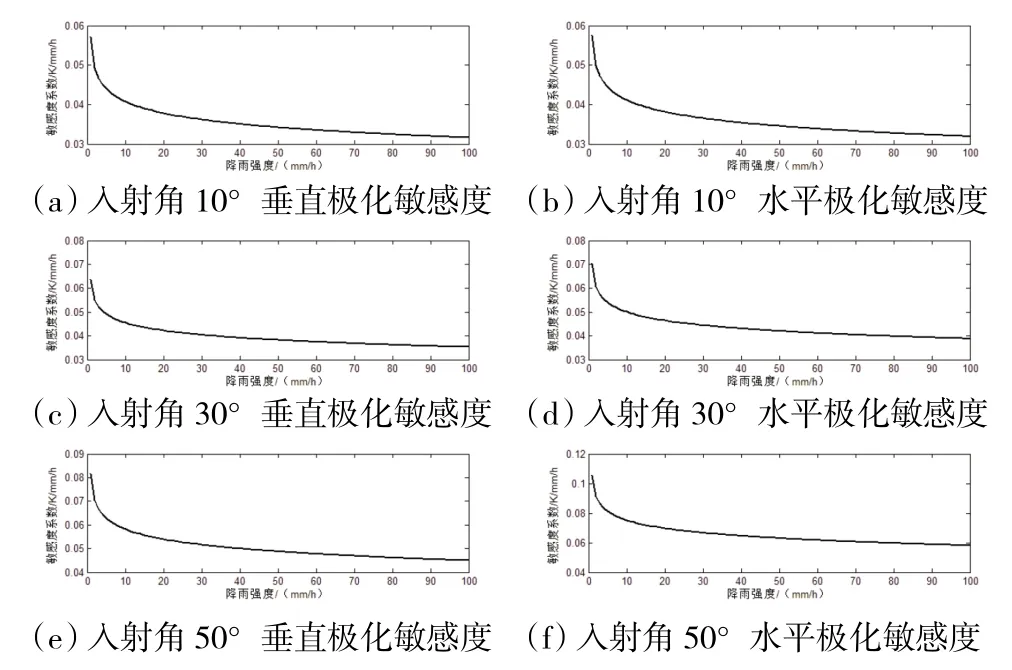
图9 亮温对降雨强度敏感度的变化

2.5 法拉第旋转角的敏感性分析

假设海表面盐度为35 psu，海面温度为290 K，海表气温为288 K，海面气压为1 013 hPa，海面风速为5 m/s，水汽含量为30 kg/m2，风向与辐射计观测方位角的相对夹角为0°。那么当辐射计入射角分别为 10°，30°，50°时，敏感度系数随法拉第旋转角的变化如图10所示。

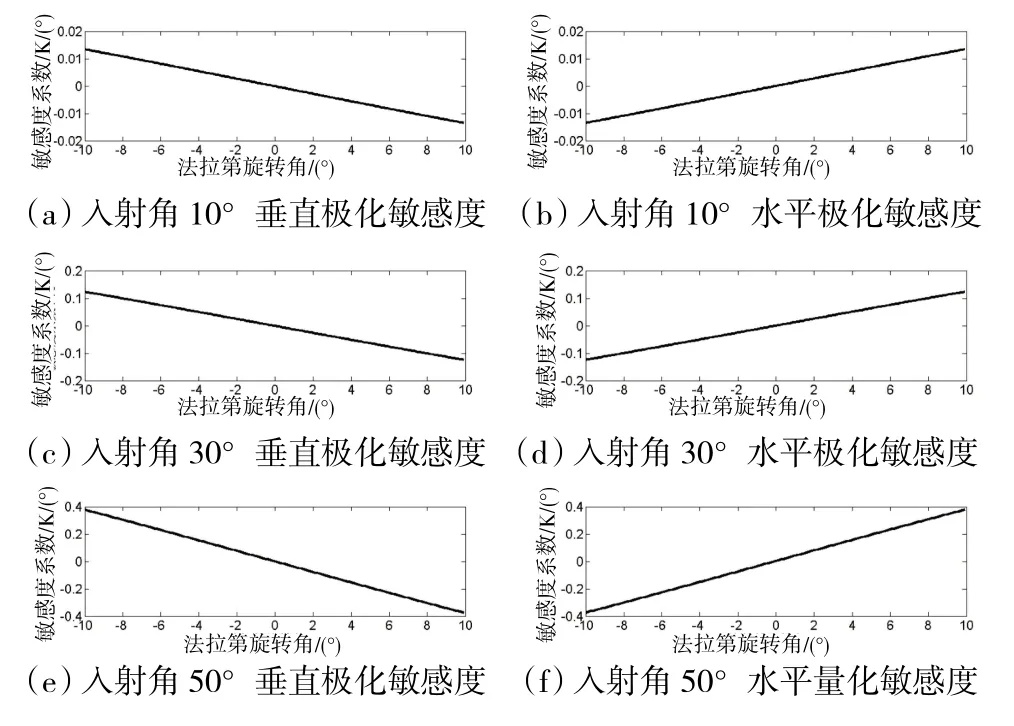
图10 亮温对法拉第旋转角敏感度的变化

由图10可以看出，当法拉第旋转角为正值时，垂直极化通道亮温和水平极化通道亮温对法拉第旋转角的敏感度系数都随着法拉第旋转角的增大而增大，负值时相反，同时也随着入射角的增大而增大。在入射角为10°时，其敏感度系数很小，约为-0．013 K/(°)～ 0．013 K/(°)，入射角为 30°时，敏感度系数约为-0．1 K/(°)～0．1 K/(°)，而当入射角为 50°时，敏感度系数约-0．4 K/(°)～0．4 K/(°)。因此，在小入射角条件下，法拉第旋转角的变化对辐射计观测亮温的影响很小，对盐度反演精度的影响可以忽略不计。在入射角和法拉第旋转角都较大时，法拉第旋转角的变化对辐射计观测亮温较为显著。

3 结论

本文利用L波段辐射传输正演模型，分析了辐射计观测亮温对海表面盐度、温度、海面风速、海面风向、海面气压、海表气温、大气水汽含量、降雨以及法拉第旋转角的敏感性特征，得出了以下主要结论：

（1）辐射计观测亮温对海表面盐度在低盐度条件下不敏感，而在正常盐度以及高盐度条件下较为敏感。亮温对海表面盐度在低温条件下也不敏感，在高温条件下较为敏感，其敏感性随着海水温度的升高而升高。

（2）辐射计观测亮温对海面温度在通常条件下敏感性较低，在低温低盐条件下，亮温对海面温度的敏感性较强，而此条件下亮温对海表面盐度的敏感性却不强。因此低温低盐条件的盐度反演精度要受海水温度资料精度的影响程度较大。

（3）辐射计观测亮温对海面风速的敏感性较高，风速越大，越加敏感。垂直极化通道亮温对风速的敏感性随着入射角的增大有明显的下降，水平极化通道亮温对风速的敏感性在大风速段也随着入射角的增大而有一定下降。因此大入射角有利于减少海面风速误差对盐度反演精度的影响。海面风向的变化对亮温观测有一定的影响，但要远小于海面风速对亮温的影响。

（4）辐射计观测亮温对大气模块部分的海表气温、海面气压、水汽含量以及降雨强度等输入参数的敏感度系数均较小，因此大气部分的环境参数不是影响亮温观测的主要因素，这里需要强调的是降雨强度变化对亮温观测影响不大的前提是已将降雨纳入到正演模型中去，但是如果在有降雨时未将其纳入到正演模型中去，则影响较大。

（5）辐射计观测亮温对法拉第旋转角的敏感性随法拉第旋转角的增大而增大，在小入射角的条件下，法拉第旋转效应的影响十分微弱。在大入射角条件下，法拉第旋转效应的影响较为明显。

[1]殷小军,张庆君,王睿，等.海洋盐度探测卫星的现状分析和未来趋势[J].航天器工程,2016,25(1):119-123.

[2]张培昌,王振会.大气微波遥感基础[M].北京：气象出版社,1995.

[3]Klein L,Swift C.An improved model for the dielectric constant of sea water at microwave frequencies[J].Antennas and Propagation,IEEE Transactions on,1977,25(1):104-111.

[4]Meissner T,Wentz F J.The emissivity of the ocean surface between 6 and 90 GHz over a large range of wind speeds and earth incidence angles[J].Geoscience and Remote Sensing,IEEE Transactions on,2012,50(8):3004-3026.

[5]Blanch S,Aguasca A.Seawater dielectric permittivity model from measurements at L band[C]//Geoscience and Remote Sensing Symposium,2004.IGARSS'04.Proceedings.2004 IEEE International.IEEE,2004,2:1362-1365.

[6]Lang R H,Jin Y,Utku C,et al.A new model function for the permittivity of seawater at 1.413 GHZ[C]//Microwave Radiometry and Remote Sensing of the Environment(MicroRad),2010 11th Specialist Meeting on.IEEE,2010:121-123.

[7]Yin X,Boutin J,Martin N,et al.Optimization of L-band sea surface emissivity models deduced from SMOS data[J].IEEE Transactions on Geoscience and Remote Sensing,2012,50(5):1414-1426.

[8]Kudryavtsev V N,Makin V K,Chapron B.Coupled sea surface-atmosphere model:2.Spectrum of short wind waves[J].Journal of Geophysical Research:Oceans,1999,104(C4):7625-7639.

[9]Gabarró C,Font J,Camps A,et al.A new empirical model of sea surface microwave emissivity for salinity remote sensing[J].Geophysical Research Letters,2004,31(1):169-178.

[10]T Meissner,F Wentz,G Lagerloef,et al.The Aquarius salinity retrieval algorithm[C]//the 12th Specialist Meeting on Microwave Radiometry and Remote Sensing of the Environment，Rome,Italy,2012.

[11]王迎强,严卫,严明.基于星载微波辐射计的海面风场对海表盐度反演影响研究[J].遥感技术与应用,2016,31(6):1037-1044.

[12]Ulaby F T,Moore R K,Fung A K.Microwave remote sensing active and passive-volume III:from theory to applications[J].Artech House Inc,1986,22(5):1223-1227.

[13]Zine S,Boutin J,Font J,et al.Overview of the SMOS sea surface salinity prototype processor[J].Geoscience and Remote Sensing,IEEE Transactions on,2008,46(3):621-645.

[14]Liebe H J,P W Rosenkranz,G A Hufford.Atmospheric 60-GHz oxygen spectrum:New laboratory measurements and line parameters[J].Journal of Quantitative Spectroscopy&Radiative Transfer,1992,48,629-643.

[15]Rosenkranz P.Water vapor microwave continuum absorption:A comparison of measurements and models[J].Radio Science,1998,33(4):919-928.

[16]Liebe H J.MPM-An atmospheric millimeter-wave propagation model[J].International Journal of Infrared and Millimeter Wave,1989,10(6):631-650.

[17]Liebe H J,Hufford G A,Cotton M G.Propagation modeling of moist air and suspended water/ice particles at frequencies below 1000 GHz[C]//AGARD 52nd Specialists'Meeting of the Electromagnetic Wave Propagation Panel,3.1-3.10AGARD,Loughton,Essex,1993.

[18]Yueh S H.Estimates of faraday retation with passive microwave polarimetry for microwave remote sensing of earth surfaces[J].IEEE Trans Geosic Remote Sens,2000,38(5):2434-2438.

[19]蔡毅.敏感性分析综述[J].中国学术期刊文摘,2008,14(11):1-1.