MY准则解析受内压薄圆环极限压力

章顺虎，姜兴睿

（苏州大学 沙钢钢铁学院，江苏 苏州 215021）

MY准则解析受内压薄圆环极限压力

章顺虎，姜兴睿

（苏州大学 沙钢钢铁学院，江苏 苏州 215021）

目的 探明受内压薄圆环极限承压能力。方法 首次以MY（平均屈服）准则对受内压薄圆环进行弹塑性分析，克服Mises准则数学求解的困难性，导出塑性区内的应力场，并获得塑性极限压力的解析解。此外，还给出了弹塑性临界半径与内压之间的依赖关系，并分析了二者间的变化规律。结果 塑性极限压力的解析解表明，塑性极限压力是材料屈服强度、半径比值的函数；与已有的Tresca、TSS准则获得的结果比较表明，Tresca准则给出极限压力下限，TSS屈服准则给出极限压力上限，MY准则给出极限压力居于两者之间，可作为Mises解的替代。结论 文中结果对于充分发挥材料性能，进而对薄圆环的设计、选材以及安全评估具有实际工程意义。

MY准则；薄圆环；应力场；极限压力；解析解

金属薄圆环是一种典型的工程结构件，在建筑、航空、机械等领域具有较为广泛的应用[1]。薄圆环受内压作用是其常见的受力形式，求解该载荷作用下的塑性极限压力对充分发挥材料潜力具有实际工程意义[2]。目前通过联解平衡微分方程、屈服条件及边界条件求解薄圆环极限压力的传统方法已近成熟[3—4]，Tresca准则因忽略中间主应力的影响而常给出偏低结果；TSS准则给出结果偏高，浪费材料；Mises屈服条件由于其非线性，获得解析解困难，目前鲜见报道[5—6]。基于以上考虑，文中采用与Mises非线性屈服准则非常逼近的线性 MY屈服准则对受内压作用薄圆环进行弹塑性极限分析，获得了薄圆环全部进入塑性状态时极限压力解析解，并定量分析了弹塑性临界半径与内压之间的变化规律。文中研究可为薄圆环的选材、设计以及安全评估提供理论依据。

1 MY准则

MY准则[7]已在材料成形[8—10]和爆破压力[11]等领域获得应用。设主应力其表达式见式(1)。该准则在π平面上屈服轨迹见图1，其中双剪应力(TSS)屈服轨迹是 Mises圆的外切正六边形[12]，Tresca屈服轨迹为Mises圆的内接正六边形，而MY屈服轨迹是非常逼近Mises圆的十二边形[7]，其屈服函数为TSS与 Tresca屈服函数的平均值。平面应力下的屈服轨迹见图2。由式(1)可得MY准则在平面应力下(σ2=0)的表达式见式(2)。

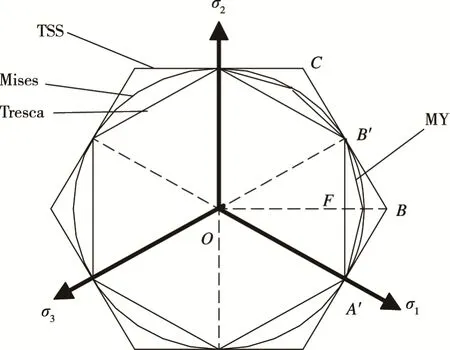
图1 π平面上的MY屈服轨迹Fig.1 MY yield locus in π-plane

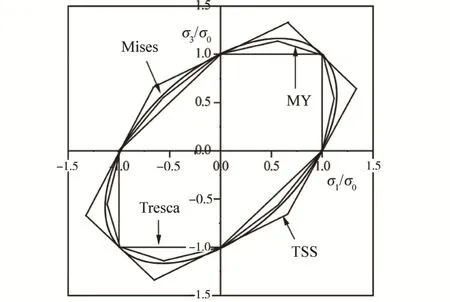
图2 双轴应力的MY屈服轨迹Fig.2 MY yield locus in biaxial stress

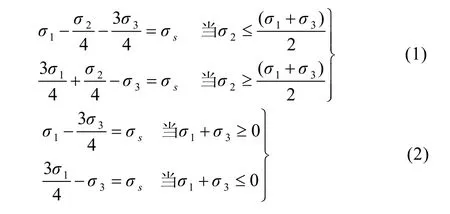
2 薄圆环的弹塑性极限分析

受内压p作用的薄圆环见图3。其中，ra和rb分别为薄圆环的内径与外径，rc为弹塑性临界半径。

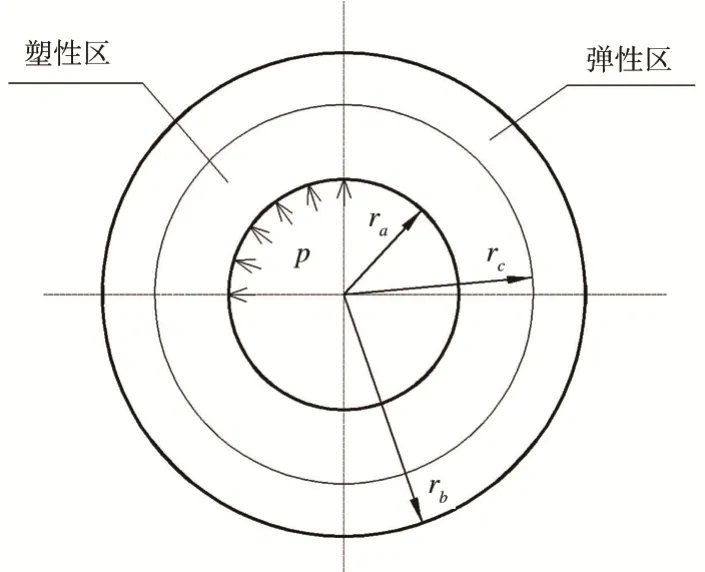
图3 受内压薄圆环Fig.3 Thin ring under internal pressure

2.1 弹性极限压力

当内压较小时，此时整个薄圆环均处于弹性状态，此时圆环的应力场为[13]：

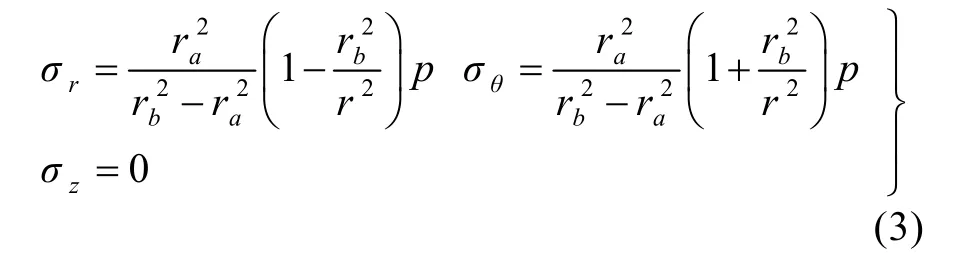
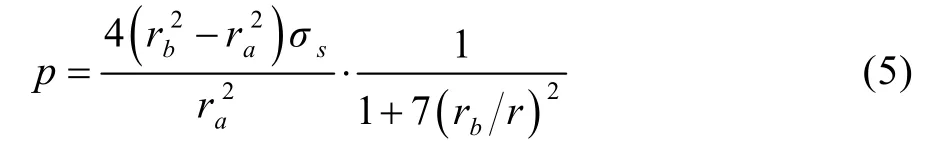
由式(5)可见，载荷p在区间[ra,rb]为r的单调增函数，因此，圆环内壁处对应的内压最小，弹性极限压力pe在r=ra处取得，为：

弹性极限压力随着半径比值的变化曲线见图4。可见，随着半径比值的增加，弹性极限压力增加。

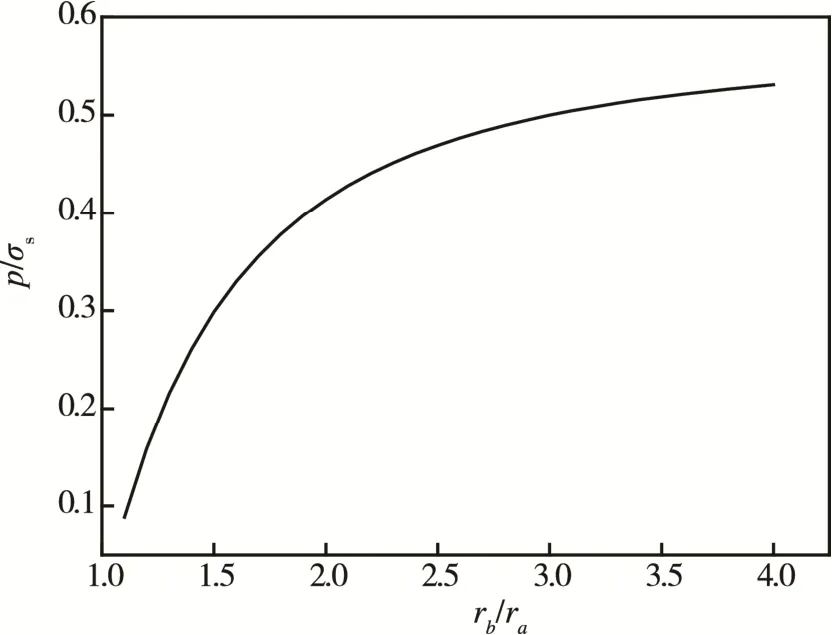
图4 弹性极限压力与半径比值的关系Fig.4 Relationship between elastic limit load and radius ratio

2.2 塑性极限压力

当内压p大于弹性极限压力后，圆环的塑性区将从内壁向外壁扩展，形成如图 3所示的内层塑性区和外层弹性区其中，在塑性区中，应力分量满足如下平衡微分方程和边界条件：

联立式(2)的第一式、式(7)和式(8)，可得塑性区应力场为：

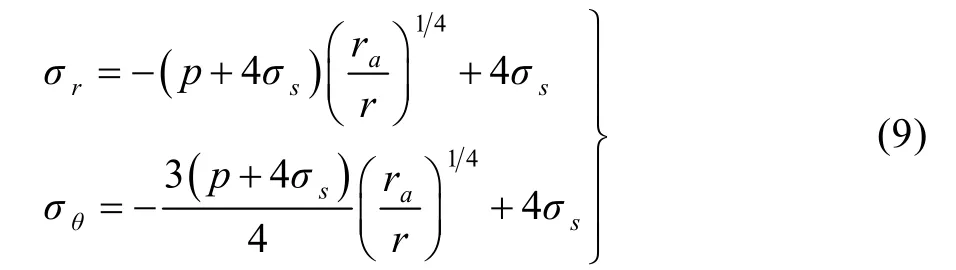
在弹性区内，参照应力场表达式(3)，可设预先满足微分方程(7)的通解表达式为：

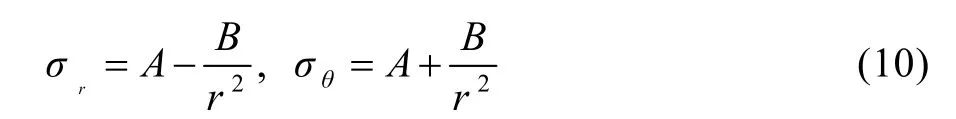
式(10)在r=rc时，σr连续，且满足应力边界条件于是，待定系数A,B如下：

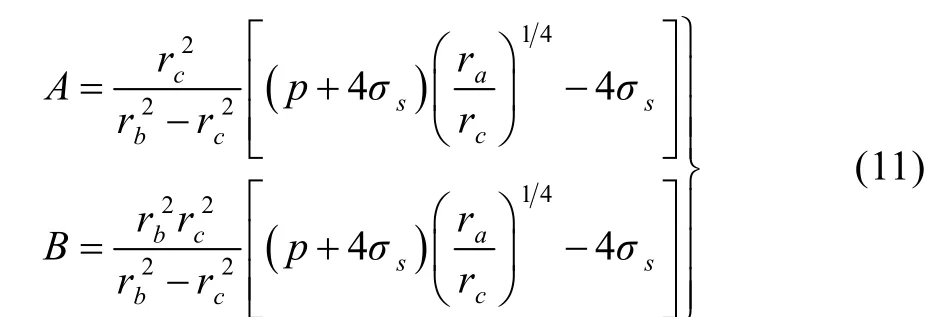
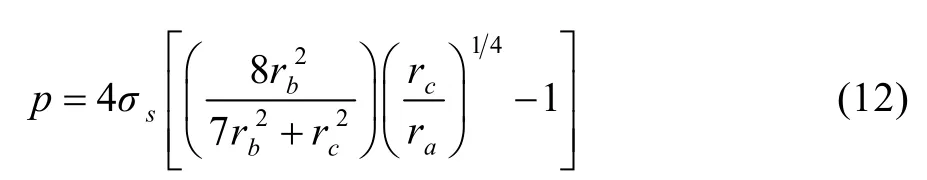
将式(11)、(12)代入到式(10)，可得塑性区范围内应力场为：

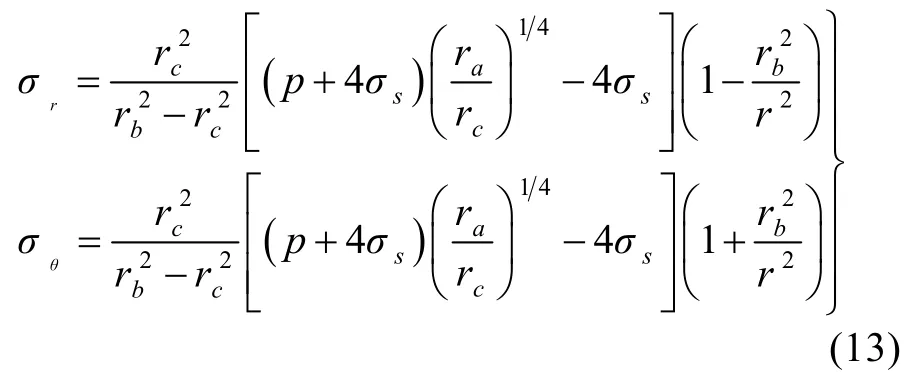
随着内压p增加，塑性区逐渐从rc范围内扩展到外径rb，因此，极限压力在整个圆环进入塑性状态时求得，见式(14)，该式表明，塑性极限压力是屈服强度与半径比值的函数。

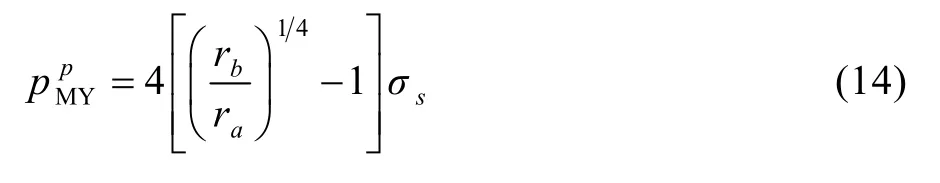
3 分析与讨论

对于本文求解对象，采用相同的解析方法，赵均海给出的Treaca解[5]和刘协权给出的TSS解[6]如下：

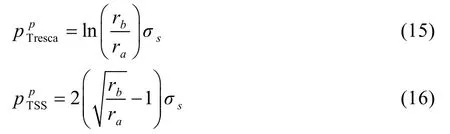
MY解与Tresca解、TSS解的对比情况见图5。可见，随着半径比值的增大，极限压力均增大，其中TSS提供极限压力上限，Tresca提供下限，MY准则居于二者之间。考虑MY准则对Mises准则具有较高的线性逼近程度，因此本文MY解可作为Mises解的替代。时的值从1开始，每隔0.5（增量）递增至比值为5条件下的关系曲线见图6。图6表明，内压随着弹塑性临界半径的增大而增大，当rc=rb，内压达到最大，为塑性极限压力条件下，塑性区内应力场分布见图7，可知，径向应力σr为负，为压应力，且随着半径r的增大而减小；周向应力σθ为正，为拉应力，且随着半径r的增大而增大。此外，因最大主应力为σθ，两应力始终存在着的大小关系。

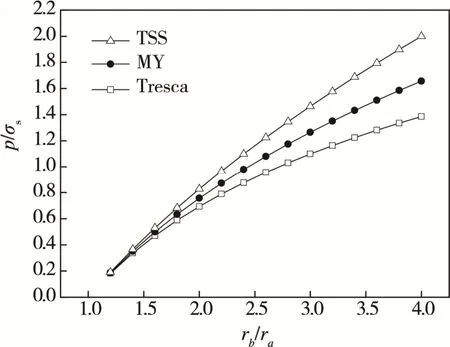
图5 依赖于屈服准则的塑性极限压力Fig.5 Plastic limit pressure depending on yield criteria

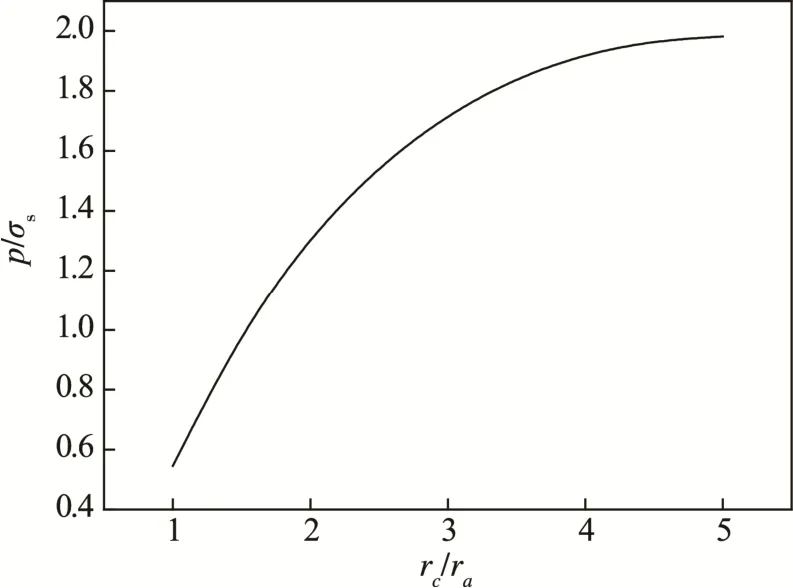
图6 内压与弹塑性临界半径间的变化关系Fig 6. Relationship between internal pressure and elastic-plastic critical radius

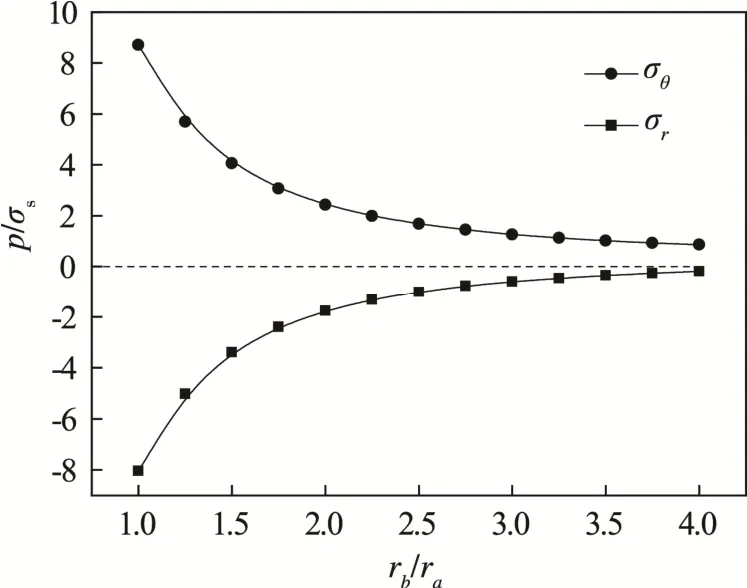
图7 塑性区内应力场分布Fig.7 Stress field distribution in plastic zone

4 结论

1) 圆环内壁处最先达到弹性极限状态，求得的弹性极限压力依赖于半径比值与屈服强度，随着半径比值的增大而增大。

2) 理论导出了受内压作用薄圆环塑性区内的应力场。分析表明，塑性区内的径向应力为负，周向应力为正。

3) 首次以 MY准则获得圆环内压条件下塑性极限压力解析解。结果表明，极限压力是半径比值与屈服强度的函数，随着半径比值的增大而增大。MY准则预测的塑性极限压力介于Tresca与TSS极限压力之间，可作为Mises解的替代。

4) 内压与弹塑性临界半径的关系表明，内压随着临界半径由内径向外径推移，不断增大，最终在外径处获得塑性极限压力。

[1] 叶开沅, 汤任基, 甄继庆. 非均匀变截面弹性圆环在任意载荷下的弯曲问题[J]. 应用数学和力学, 1981, 2(1):1—12.YE Kai-yuan, TANG Ren-ji, ZHEN Ji-qing. Bending of Non-homogeneous Variable Thickness Elastic Circular Ring Under Arbitrarily Distributed Loads[J]. Applied Mathematics and Mechanics, 1981, 2(1): 1—12.

[2] KIM N H, OH C S, KIM Y J, et al. Limit Loads and Fracture Mechanics Parameters for Thick-walled Pipes[J].International Journal of Pressure Vessels and Piping, 2011,88(10): 403—414.

[3] SAVE M A. Plastic Analysis and Design of Plates, Shells and Disks[M]. Netherland: North Holland Pub Co., 1972.

[4] BOYLE J T, HAMILTON R, SHI J, et al. A Simple Method of Calculating Lower Bound Limit Loads for Axisymmetric Thin Shells[J]. Journal of Pressure Vessel Technology, 1997, 119(2): 236—242.

[5] 赵均海, 顾强. 薄圆环极限载荷统一解[J]. 西安建筑工程学院学报(自然科学版), 2001, 18(1): 1—4.ZHAO Jun-hai, GU Qiang. Unified Ultimate Load Solution of Thin Ring[J]. Journal of Architecture and Civil Engineering (Natural Sciences), 2001, 18(1): 1—4.

[6] 刘协权, 倪新华, 焦耀斌. 用双剪强度理论计算拉压异形材料薄圆环的极限载荷[C].“力学2000”学术大会论文集, 2000年.LIU Xie-quan, NI Xin-hua, JIAO Yao-bin. Limit Load Calculation of Thin Ring of S-D Effect Material with TSS Theory[C]. “Mechanics 2000” Conference Prceedings of Academic Conference, 2000.

[7] 赵德文, 刘相华, 王国栋. 依赖Tresca与双剪屈服函数均值的屈服准则[J]. 东北大学学报(自然科学版), 2002,23(10): 976—980.ZHAO De-wen, LIU Xiang-hua, WANG Guo-dong.Yield Criterion Based on the Mean Function of Tresca and Twin Shear Stress Yield Functions[J]. Journal of Northeastern University: Natural Science, 2002, 23(10):976—979.

[8] ZHAO De-wen, XIE Ying-jie, WANG Xiao-wen, et al.Derivation of Plastic Work Rate Per Unit Volume for Mean yield Criterion and Its Application[J]. Journal of Material Science Technology, 2005, 21(4): 433—437.

[9] ZHANG Shun-hu, SONG Bin-na, WANG Xiao-dong, et al. Analysis of Plate Rolling by MY Criterion and Global Weighted Velocity Field[J]. Applied Mathematical Mod-eling, 2014, 38(14): 3485—3494.

[10] ZHANG Shun-hu, CHEN Xiao-dong, HOU Ji-xin. Analysis of Broadside Rolling for Heavy Plate by Weighted Velocity Field and Mean Yield Criterion[J]. Meccanica,2016, 51(5): 1189—1199.

[11] 李灿明, 赵德文, 章顺虎, 等. MY准则解析 X80钢油气输送管道爆破压力[J]. 东北大学学报(自然科学版),2011, 32(7): 964—967.LI Can-ming, ZHAO De-wen, ZHANG Shun-hu, et al.Analysis of Burst Pressure for X80 Steel Pipeline with MY Criterion[J]. Journal of Northeastern University(Natural Science), 2011, 32(7): 964—967.

[12] YU M H. Twin Shear Stress Yield Criterion[J]. International Journal of Mechanical Science, 1983, 25: 71—74.

[13] 刘士光, 张涛. 弹塑性力学基础理论[M]. 武汉: 华中科技大学出版社, 2008.LIU Shi-guang, ZHANG Tao. Elastoplastic Mechanics Theory[M]. Wuhan: Huazhong University of Science and Technology Press, 2008.

[14] 同济大学数学系. 高等数学(下册)[M]. 北京: 高等教育出版社, 2009.Mathematics Department of Tongji University. Advanced Mathematics[M]. Beijing: Higher Education Press, 2009.

[15] 章顺虎, 赵德文, 王力, 等. MY准则解析线性和均布载荷下简支圆板的极限载荷[J]. 东北大学学报(自然科学版), 2012, 33(7): 975—978.ZHANG Shun-hu, ZHAO De-wen, WANG Li, et al. Limit Load Analysis of Simply Supported Circular Plate Under Linearly and Uniformly Distributed Load with MY Criterion[J]. Journal of Northeastern University (Natural Science), 2012, 33(7): 975—978.

Analysis of Limit Pressure for Thin Ring Subjected to Internal Pressure with MY Criterion

ZHANG Shun-hu,JIANG Xing-rui
(Shagang School of Iron and Steel, Soochow University, Suzhou 215021, China)

To clarify the ultimate loading capacity of thin ring subjected to internal pressure, the elastic-plastic analysis of thin ring under internal pressure was first carried out with MY criterion to overcome the difficulty of mathematical solving of Mises criterion. The stress field in the plastic zone was derived, and an analytical solution of plastic limit load was then deduced.The dependency relationship between elastic-plastic critical radius and internal pressure was given. And the change rules of them were analyzed. It was shown in the solution that the plastic limit pressure was a function of yield stress and radius ratio. By comparing the plastic limit pressure with those obtained based on Tresca and TSS, Tresca criterion provided a lower bound, TSS provided an upper bound, while the solution of the MY criterion lay between them, and could be taken as the approximation of Mises solution. The present result has realistic engineering significance in full using of material properties, and further in guiding of the design, material selecting, and safety assessment of thin ring.

MY criterion; thin ring; stress field; limit pressure; analytical solution

2017-11-15

国家自然科学基金（51504156）；江苏省基础研究计划（自然科学基金）（BK20140334）；江苏省高校自然科学研究（14KJB460024）；中国博士后科学基金（2014M561707）

章顺虎（1986—），男，副教授，主要研究方向为塑性成形理论与工艺。

10.3969/j.issn.1674-6457.2018.01.015

TG301

A

1674-6457(2018)01-0122-05