基于区间集对势的土体胀缩性评价模型

李亚峰, 汪明武, 朱 宇, 金菊良

(合肥工业大学 土木与水利工程学院,安徽 合肥 230009)

基于区间集对势的土体胀缩性评价模型

李亚峰, 汪明武, 朱 宇, 金菊良

(合肥工业大学 土木与水利工程学院,安徽 合肥 230009)

文章应用区间数和集对分析耦合理论,探讨了膨胀土与石灰改良土的胀缩性区间集对势评价模型。该模型首先基于区间数表达实测指标和评价标准,进而转换为联系数,以计算集对势及构建评价标准的区间集对势,进而统一分析样本与评价标准间的同异反关系态势与判定样本的胀缩性等级。结果表明,该模型应用于膨胀土和石灰改良土胀缩性评价是有效可行的,且能充分表达评价指标区间动态变化特点和从势角度分析胀缩性转换态势,并解决了区间数难于对比分析的难题,也为其他类似不确定性问题分析提供了参考。

区间数;集对势;胀缩性;评价

膨胀土具有吸水膨胀和失水收缩的显著特性,且具有长期反复的特性,对工程安全具有潜在危害性,故工程界常用掺石灰方法来改良膨胀土,但改良后的土收缩性对工程仍有影响[1-4]。因此,膨胀土和改良土的胀缩性等级评价对确定合理工程措施和确保工程安全具有重要意义。然而,膨胀土胀缩性评价受诸多不确定性因素影响,是一个复杂的不确定系统分析问题,虽然以往人们针对该问题提出了可变模糊集法[5]、联系期望值法[6]和可拓方法[7]等方法,但这些方法大多基于实测指标均值表达,而实测样本指标值常表现为区间数特点,因此这些方法评价结果往往同实际情况存在差异,显然土体胀缩性等级评价问题至今尚未得到很好的解决。为此,本文应用更贴近实际指标特点的区间数来表达胀缩性评价问题,并应用集对分析耦合方法统一分析样本与评价标准间的同异反关系,并从势的角度深入挖掘分析胀缩性等级转换问题,从而真实反映样本所能提供的动态多元信息,使评价结果更符合事物的客观本质及表征指标的动态不确定性,从而达到提高膨胀性等级评价的可靠性和准确性。

1 区间集对势评价模型

1.1 基本原理

基于区间联系势评价的基本原理如下:基于区间数表达实测样本指标值和评价标准集界限点,并转换为联系数计算样本的集对势值和评价标准的区间集对势,以便于分析样本和评价标准区间数间的关系;进而判定待评样本集对势与评价标准区间集对势间的同异反关系,确定待评样本的等级。

1.2 区间集对势定义

因为不确定性问题属性常常是一个范围值,所以用区间数能较好描述和刻画不确定属性。二元区间数的定义如下:若设∀xL,xU∈R,且xL≤xU,则称[x]为二元区间数,其中xL和xU分别称为下极限和上极限,若xL=xU,则区间数退化为普通的实数。目前区间数理论和应用尚不成熟,特别是2个区间数之间的关系研究,因此本文引入集对势来分析2个区间数之间的联系及相互转化态势。

基于整体思维的势科学认为事物差别促进联系,联系扩大差别。集对势则是集对分析理论中一种处理同异反联系转化态势的分析理论[8-10]。集对分析把不确定性与确定性统一在一个同异反系统中进行辨证分析和数据挖掘,并用联系数刻画集对的同异反关系及演化态势,相应的数学模型为:

μ=a+bi+cj

(1)

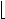
μ=γL+(γU-γL)i+(1-γU)j

(2)

其中,γL、γU为区间数的下限和上限;μ为区间数转换后的联系数,则相应的区间集对势可定义如下：

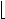
(3)

其中,[SPP(H)]为区间数表达形式的联系势,在此定义为区间集对势;SPP(H)为相应联系数集对势;n为样本m的指标数。可见,区间集对势是分析区间数间同异反关系的一种有效方法。

1.3 评价流程

基于区间联系势的评价模型操作步骤如下。

(1) 基于区间数形式表达待评样本和评价标准。若[xmn]表示第m个样本的n指标实测值,则它们相应的区间数矩阵X为：

X=[xmn]M×N=

相应n指标p等级的区间数表达形式为基于界限点的区间数,则基于等级[qpn]的上、下限点可构造成区间数形式Q:

(6)

其中,qpn为n指标p等级标准的下限或上限。

(2) 区间数矩阵规范化。因不同指标或者属性之间一般存在不可公度性和矛盾性,为消除量纲、数量级和类型对决策或者评价结果的影响,需进行指标规范化处理。本文采用极差变化法,将集合X和Q转化为规范化矩阵Y和Z,具体方法为：

(3) 加权规范化矩阵构建。若评价指标的权重为W={ω1,ω2,…,ωN},则加权后Y和Z可表示为L和K,即

(11)

(4) 区间数矩阵元素转化为联系数,并计算样本集对势和构建评价标准区间集对势以判定等级。经加权规范化后区间数实质上是一种差别与距离相比较的势,表达了样本胀缩性趋向等级高的态势,则样本的联系数μm、区间集对势SPP(H)m、评价标准的集成联系数μp和区间集对势SPP(H)p可依据(2)～(4)式分别求出,并通过比较待评样本的集对势和区间数形式表达评价标准集对势,即可确定待评样本的等级。

2 实例应用

实例采用文献[6]中的合肥新桥机场膨胀土现场实测和室内实测资料,应用区间数集对势评价模型进行等级评价并与其他分析方法的结果进行对比研究,以验证讨论模型的可行性和可靠性。实例中选取了液限、胀缩总率、塑性指数、天然含水率和自由胀缩率等5个指标,胀缩性等级划分为Ⅰ(极高)、Ⅱ(高)、Ⅲ(中)和Ⅳ(低)4个等级[12]。胀缩性等级评价指标标准见表1所列,取评价指标标准的界限点值用区间数的形式表达,见表2所列。样本的实测值见表3所列,权重直接采用文献[6]中数据,即ωj={0.23,0.22,0.20,0.19,0.16},∑ωj=1。依据(2)式、(4)式、(7)式、(11)式可得区间界限点和样本的集成联系数和区间集对势，结果见表4所列。按评价准则可得样本的胀缩性等级,实例评价结果及与其他方法对比结果见表5所列。

由表5结果可知,实例应用中基于区间集对势评价模型的分析结果与其他方法结果基本吻合,表明该方法应用于膨胀土等级评价是有效可行的。同时,可变模糊集方法中隶属函数的确定具有一定的主观性,且对区间数提供的不确定性信息没有充分利用。而联系期望法则侧重于实测指标的均值,对样本向其他等级的转化态势没有很好地刻画。而本文模型通过引入区间集对势的概念,不仅有效表达了样本实测值的区间变化特征,而且可定量表达与分类标准之间的同异反关系以及向其他等级转化的态势,显然避免了基于实测指标均值的缺陷,有利于表达和挖掘样本指标的确定性与不确定性,达到简洁有效地刻画指标所包含的各类有用信息的目的。

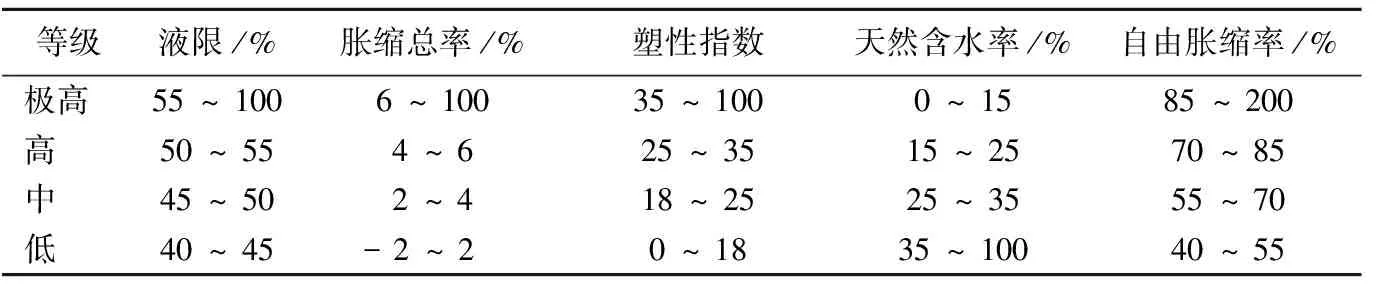
表1 胀缩性等级评价指标标准

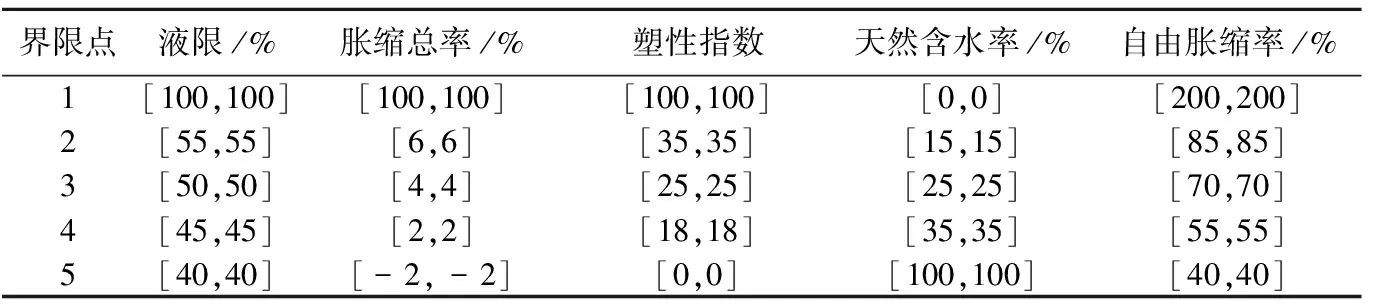
表2 胀缩性等级评价指标界限点的区间数表达

基于区间数转化为联系数,以集对势分析样本的确定性与不确定性转换态势,有利于分析样本胀缩性发展趋势,从而真实地反映样本的胀缩特性与确定等级。因此,区间集对势评价模型能充分表达评价指标区间动态变化特性,且克服了传统区间数分析方法难于对比的缺陷。

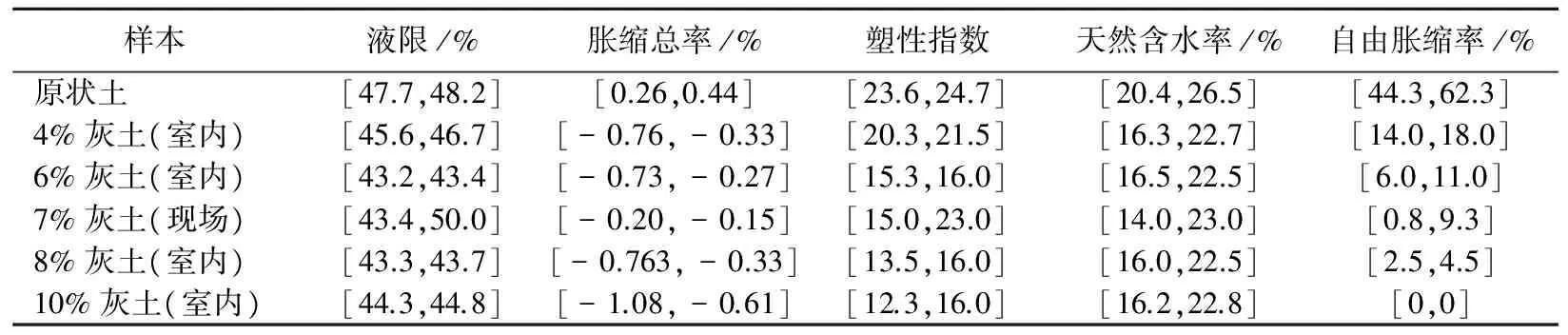
表3 区间数表达的实测评价指标

表4 胀缩性等级评价标准的区间集对势表达

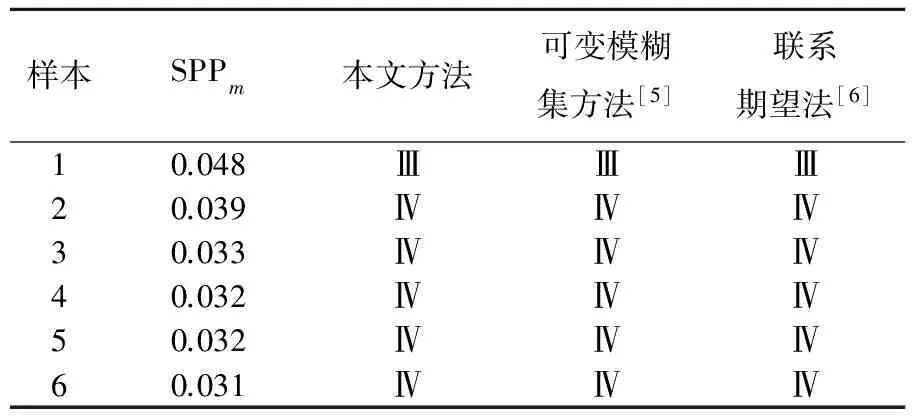
表5 实例样本联系数与结果对比

3 结 论

土体胀缩性等级评价涉及多类型的动态复杂信息,是一个极为复杂的不确定性难题。本文基于区间集对势概念,探讨了胀缩性等级的区间集对势评价模型,实例应用和与其他方法对比结果表明，该模型不仅克服了传统方法基于均值表征样本指标与实际指标分布不符的缺陷，解决了以往区间数分析过程繁琐的难题,而且能反映样本胀缩性等级的转化态势,为土体胀缩性动态分析提供了新的方法。

[1] 刘松玉,季鹏,方磊.击实膨胀土的循环膨胀特性研究[J].岩土工程学报,1999,21(1):9-13.

[2] 唐朝生,施斌.干湿循环过程中膨胀土的胀缩变形特征[J].岩土力学,2011,33(9):1376-1384.

[3] 查甫生,崔可锐,刘松玉,等.膨胀土的循环胀缩特性试验研究[J].合肥工业大学学报(自然科学版),2009,32(3):399-402.

[4] WANG M,LI J,GE S,et al.Moisture migration tests on unsaturated expansive clays in Hefei,China[J].Applied Clay Science,2013,79:30-35.

[5] 罗文柯,杨果林.模糊数学对湖南膨胀土分类与判别实际工程应用研究[J].南华大学学报(自然科学版),2006,20(2):12-16.

[6] 汪明武,赵奎元,张立彪.基于联系期望的膨胀土和改良土胀缩性评价模型[J].岩土工程学报,2014,36(8):1553-1557.

[7] 汪明武,金菊良,李丽.可拓学在膨胀土胀缩等级评判中的应用[J].岩土工程学报,2003,25(6):754-757.

[8] 赵克勤.集对分析及其初步应用[M].杭州:浙江科学技术出版社,2000.

[9] 张清河.多元联系数在地基处理方案模糊选优中的应用[J].水文地质工程地质,2005(6):112-115.

[10] 童英伟,刘志斌,常欢,等.集对分析法在河流水质评价中的应用[J].安全与环境学报,2008,8(6):84-86.

[11] 汪明武,金菊良,周玉良.集对分析耦合方法与应用[M].北京:科学出版社,2014.

[12] 王广月,马华月,刘健.路基膨胀土胀缩等级的物元可拓识别模型[J].公路交通科技,2005,22(11):30-33.

Anovelevaluationmodelforswelling-shrinkagegradeofsoilmassbasedonintervalpotentialofsetpair

LI Yafeng, WANG Mingwu, ZHU Yu, JIN Juliang

(School of Civil and Hydraulic Engineering, Hefei University of Technology, Hefei 230009, China)

Based on the interval number theory and set pair analysis, the evaluation model for the swelling-shrinkage behaviors of expansive soil and lime improved soil using interval potential of set pair was discussed. Firstly, interval numbers were utilized to express the variable evaluation indicators and classification standard, and were transferred into connection numbers in order to calculate the interval potential of set pair consisting of the measured indicators and boundary points of classification standard. Then the identity-discrepancy-contrary state relationship between the sample and standard as well as the swelling-shrinkage grade of the sample was determined. The results show that the proposed model, which overcomes the defect of the traditional methods which have difficulty with the comparison among interval numbers, is effective and feasible, and can fully express the changes in the evaluation indicators and depict the transformation of swelling-shrinkage grade from a perspective of connection potential. It also provides a reference for other similar uncertainty problems.

interval number; set pair potential; swelling-shrinkage behavior; evaluation

2016-05-03；

2016-06-12

国家自然科学基金资助项目 (41172274;51579059)

李亚峰(1992-),男,安徽滁州人,合肥工业大学硕士生;

汪明武(1972-),男,安徽歙县人,博士,合肥工业大学教授,博士生导师;

金菊良(1966-),男,江苏苏州人,博士,合肥工业大学教授,博士生导师.

10.3969/j.issn.1003-5060.2017.12.018

TU443

A

1003-5060(2017)12-1675-04

(责任编辑马国锋)