具有学习过程的贝叶斯决策模型与统计模拟

周丽莉，胡 军，章 昊

（南昌大学 经济管理学院，南昌 330031）

0 引言

面对复杂的市场环境，决策者将根据获得的信息不断更新自己的信念，综合后验信念和外部约束条件进行决策，即金融市场上的学习行为[1]。Matthew以及Kahneman and Smith（2002年获得诺贝尔经济学奖）都认为决策主体在有意识的识别并解释外部信息的过程中进行决策，也就是在有限的时间、知识和其他资源条件下，通过学习过程分析环境特征给出决策。市场参与者的行为受到信念影响，这种信念将随外部环境的变化而不断调整，与之相伴随的就是学习过程[2]。

对于传统风险度量方法难以描述的市场现象，在考虑市场学习行为后构建的统计模型在一定程度上能够给出解释，特别是面对以下一些难题：第一，为较少发生而影响巨大的事件指定概率是非常困难的，例如很少有先例的金融危机，这意味着在理解这些进程发展的过程中，对事件发生似然性的评估将随之改变，有时甚至是大幅度的变化[3]；第二，对于初始条件和外界扰动的变化，金融系统的行为是非常敏感的，原因可能是受限于多重均衡，表现出强烈的路径依赖和滞后现象[4]；第三，与复杂的物理系统不同，金融市场上的现象更加难以预测，因为驱动金融系统的变量与人们的认知紧密相关。金融市场参与者对于经济形势的不确定性，使其表现出更加保守的风险承担行为，这反过来进一步削弱经济发展的势头[5]。这种由学习行为获取的信念将随外部环境的变化不断调整，结果是几乎没有静态的稳定参数描述系统间变量的关系。国内近年来开始有大量的学者结合中国金融市场环境，基于学习行为和信念变化研究投资动态、消费特征以及资产价格的异常现象[6]。但是相关研究仍处于起步阶段，而且利用西方行为决策模型无法全部解释中国特定环境中出现的行为偏离现象[7]。

本文将给出考虑市场学习行为时的贝叶斯决策模型构建方法，并以消费-储蓄决策模型为例，通过数据模拟说明模型的有效性。

1 具有学习过程的贝叶斯决策模型

1.1 贝叶斯学习过程

根据近年来不确定性经济学和贝叶斯统计决策理论的最新研究进展[8]，在外部市场环境存在不确定性时，决策者在获取外部信息的过程中需要综合过去、现在和未来的信息不断学习认知，在一定的风险约束条件下，结合具体目标做出决策，其中基本的学习过程遵循贝叶斯法则（见图1）。

图1 具有学习过程的市场参与者决策过程

统计决策函数定义于样本空间而取值于行动空间。以θ表示参数，δ表示决策函数，当获取样本x后，决策者可能承担的损失为 L（θ，δ（x））。通常在损失函数达到极小值时，δ为最优决策。但损失值依赖于真实参数θ和样本x，参数值未知，同时样本具有随机性，因而需要基于损失L（θ，δ（x））的期望值构建风险函数：

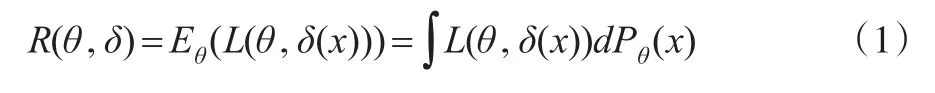
R（θ，δ）即为风险函数，其中 Eθ和 Pθ是为了强调在参数值为θ的条件下计算期望和概率[9]。传统风险度量方法中需要给出静态条件下θ的稳定估计值，而市场学习行为的存在意味着决策者在获取新的信息后将更新对θ的认知π（θ），这个更新过程就是在贝叶斯框架下描述学习过程的有效途径[10]。假定在没有获取任何信息时，当前关于θ的信念表示为期望值θ0和方差为的正态分布π0。当观测到θ的T个独立信息时，令st=θ+εt，其中εt是均值为0方差已知σ2的正态变量。根据贝叶斯法则，θ后验分布的期望值和方差分别为：

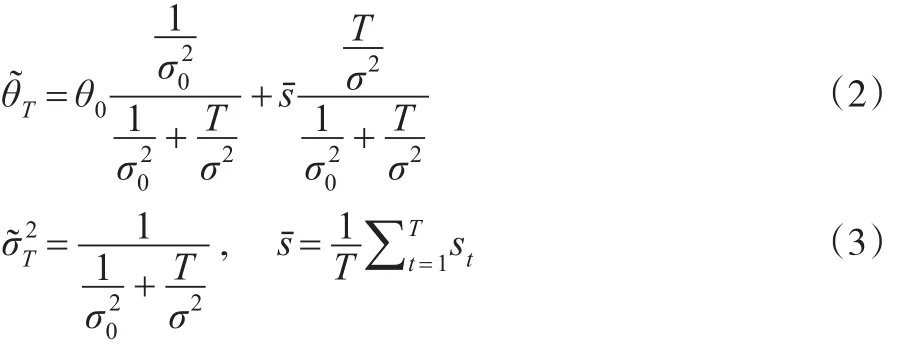
1.2 贝叶斯决策模型

首先考虑一个无限时域的决策问题，代理人具有离散形式的贴现效用：

其中折现因子λ∈[0，1]，u通常是凹性效用函数，如通常文献中采用的冯·诺依曼-摩根斯坦效用函数[11]。δi表示给定第i期约束时的行为决策变量。代理人在参数分布π（θ）和预期收益 fi的影响下进行决策以达到效用最大化：

对于储蓄-消费问题来说，并不是任何时候都有必要考察决策行为的不确定性。比如在构建模型时，仅仅是对于总消费变量存在不确定性，那么在模型中可以采用与π（θ）相同的边际分布建立决策函数，不会对期望效用的贴现值产生影响。在这种情形下，贝叶斯决策模型就退化为普通的风险度量模型。但是对于多数的市场参与者来说，都如图1所示能够在金融市场获取信息，通过认知、更新和交流。当消费者对于收入有选择储蓄减少消费，或者通过借款增加消费的自由时，这时从收入变化衍生出的间接效用就会充分的展现出具有市场学习行为时的决策特点。

为了具体说明如何构建具有学习行为的贝叶斯决策模型，首先假定在经过初始阶段的收益积累之后，才会发生消费。在收益积累之后再实行分期消费，这个假定简化了间接效用的计算，也使得学习过程表现得更加透彻，之后本文将放宽假定进一步分析当收入和财富可变时的消费-储蓄问题。当消费者察觉短期收入异常时，会将其作为长期收入预期的潜在信息，这样获取信息的学习过程导致消费出现更大的波动[12]。

在传统的风险度量方法中，通常假定决策者能够获取静态的稳定参数，或者是决策者具有参数θ可能的分布形表示在得到参数θ的估值后，基于预期收益 fi计算期望值。实际上，在这样简化的假设下U1和U2的主要区别就在于是否将参数θ视为静态的稳定参数。如果决策函数Ui对于θ是严格凸的，那么U2必然大于U1。这表明了在面对复杂的市场环境时，决策者需要不断学习获取外部信息以确定更优消费决策，帮助决策者确定最优决策的信息是具有价值的，这与不确定性经济学中决策以牺牲经济利润为代价的基本观点相一致。如果排除平滑消费的情形，U1和U2就是相等的。但是在现实的经济环境中，一定程度的消费平滑是必然存在的，从而考虑学习行为的决策模型就可以更好地解释消费行为的动态特征。为了进一步说明贝叶斯模型下决策行为与传统风险模型中的差别，取式（5）和式（6）的反函数：

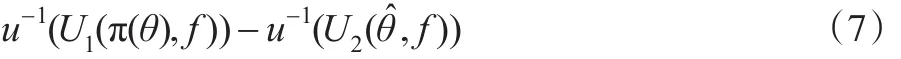
由于间接效用函数的反函数是支出函数，所以式（7）体现了由于学习行为的存在对消费流的影响。以具体消费方式为例，如资产每期都有收益，但是最终分红是在n+1期一起支付的，那么消费需要在n+1期发生，这样和收益的分离可以很容易地发现U1和U2是相等的，也就是说没有对期望效用产生影响。但是式（7）的结果却不一定为0，下面本文将通过具体的统计模拟说明考虑市场学习行为时消费流的动态特征。式，经过数据更新可以给出参数θ的估计[13]。令表示参数θ的估值，传统度量方法中的决策函数可以表示为：

2 市场学习行为对决策的影响及统计模拟

在上述的模型构建中，消费需要在收入实现之后才能发生，消费流依赖于过去实现的所有收入之和。这种简化性的假设实际上是对过去的收入做了最简单的平滑。本文将在更加贴近现实的模型中考察学习行为的影响，即放宽上述假定，允许消费流和收入流在每期都会发生。

2.1 模型的拓展

由于消费流和收入流在每期都会发生，所以每一期开始消费者都面临两个状态，真实的财富状态和在当前信息下财富的信念，分别用mt和πt表示。消费决策可以表示为状态的函数δ（wt，πt）。首先可以给出真实财富的演化过程：

其中δt是第t期的消费量，储蓄的收益率r＞0。在决策者具有市场学习过程时，信念状态的演化遵循贝叶斯法则。为了在描述学习行为下消费决策的动态特征，需要设定效用函数的具体形式，如指数形式，这里假定折现因子为最常见的形式消费的最优解应该满足欧拉方程：

对于指数效用来说，边际效用是一个常量乘以效用水平。因而通过将上式迭代推导可得任意时期的解，从而获得消费流的具体数值。

2.2 学习行为对决策的影响

针对指数形式的效用函数，已有很多研究在没有考虑市场学习行为的假定下推导出了消费流的演化过程[14]。下面给出主要的结果：

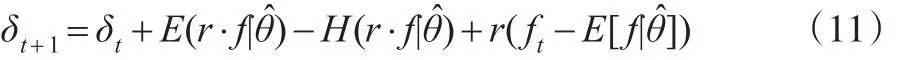
分布，可以很明显看出式（11）的最后一项期望值为0。因而中间两项的差值就是主要影响消费流的漂移项。如果 f的分布替换为均值保留展形，那么风险溢价将上升。由微观经济理论可知，凹性效用的确定性等价总是小于期望值，所以只要参数θ不是固定的静态稳定值就必然大于0。在特殊的情形下，如果未来的红利r⋅f已知，那么风险溢价为0。由此可以明确，这两项的差值存在的原因就是预防性储蓄。

为了说明学习行为对消费决策的影响，首先需要明确在指数效用形式下，风险态度与财富水平无关。这样给定参数θ的信念π，依据式（10）最优消费决策函数需满足：

δ*（π，0）表示在消费流发生的初期没有财富。原因在于风险态度与财富水平无关，所以 δ*（π）≡δ*（π，0），而且对于π来说消费函数是凸函数。接下来参照式（11）的推导过程，在具有学习行为时，也需要提取出一项风险溢价，即πt，πt+1不同信念下的消费流之差如果 π有静态的分布，可以给出θ的稳定估计值，那么这项溢价就与式（11）中的一致。如果决策者在不断获取市场信息过程中具有学习行为，则消费流的演化过程将表现出不同的动态特征。依式（12）有同时根据式（8）给出的真实财富演化过程可以得到：所以有：

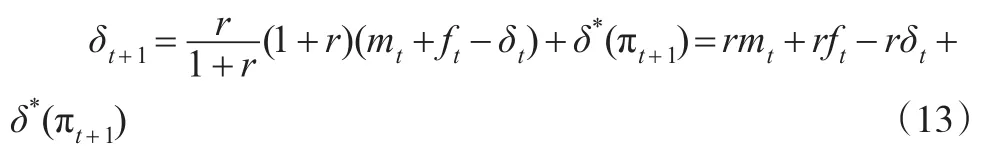
将上式按照式（11）的形式，在右端加上一项rEπt[ft]，再减去rEπt[ft]，合并后可得：

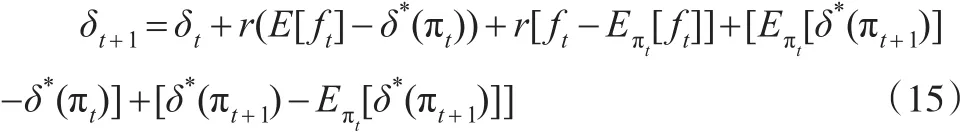
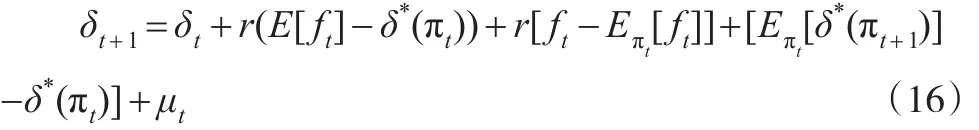
这样就得到了在具有市场学习行为时的消费决策函数的演化过程。式（16）的第一行与式（11）的表述基本一致。第二行则包含了学习过程的影响。首先从漂移项[Eπt[δ*（πt+1）]- δ*（πt）]可以看出，如果能够得到 θ 的稳定估计值，则该项为0。如果存在学习过程，则πt，πt+1分别体现了不同时点下的决策者信念，而且能够推断只要πt不是一个固定的点，那么该式严格为正（根据詹森不等式）。最后一项随机扰动项μt的存在是由于信息流的持续影响，特别是当前获取的红利是预期未来红利的重要信息，因而单纯的第t+1期消费决策和在t期信息基础上给出的第t+1期消费决策期望值会有一定差异。

2.3 统计模拟

在贝叶斯框架下，学习行为通过决策者对外部信息的信念更新表示出来，下文应用消费-储蓄模型的参数化形式通过统计模拟说明学习行为对决策的影响。

2.3.1 传统风险模型

动态经济模型中通常假定决策者对经济变量未来的变动能够做出符合理性的预期，也就是说信念与观测到的经验频率相一致。为了有效比较统计模拟结果，本文假定消费者的信念与外生收入过程观测到的经验频率相一致。在传统风险度量模型推断过程中，需要依据模型的约束以及过去一段时间内收入的观测值给出参数的稳定估计值。如果观测序列值足够多，那么估计值将概率逼近真实值θ。之后将假定决策者在获取后依据式（10）给出最优消费决策，从而估计模型其余的参数。这种跨方程限制的方法有效地将自由变量“预期”变为估计值再进行经验分析。

以具体统计模拟计算为例，假定收入是二值变量f∈{ }0，1，利率r=0.01，决定收入实现的参数真实值θ=0.7，同时消费流发生的初期没有财富。依据大量的序列观测估计得到的将逼近于0.7。由于估计方法并不是这里讨论的重点，所以为了方便起见，假定不存在抽样误差=θ。在此基础上，消费的演化过程将同样遵循自回归方程，以θ=0.7代入式（11），进而通过迭代可以模拟得到传统风险度量模型中消费函数的具体数值。

2.3.2 不确定性的影响

消费者的信念与经验分布一致暗含着两个假定：一是具有大量的观测值；二是决策者相信未来的动态与过去一致，也就是说从已有观测值推断的参数将在未来同样决定数据的分布。当存在市场学习行为时，决策者质疑用观测值估计未来参数的方法，此时不能应用稳定的静态参数值给出消费的最优决策，而是遵循式（16）的演化过程。由于市场学习行为的存在，信念状态πt是随着新出现的信息而不断更新的，这对于决策结果至关重要。在式（16）可以明显的看到，消费演化过程中多了漂移项和均值为0的扰动项。由于消费决策函数的演化无法解析推导，但是同样可以采用模拟计算的方式说明学习行为的影响。仍然假定真实参数θ=0.7，决策者在事前缺乏足够的信息，选择位于区间[0，1]上的均匀分布π作为初始信念。从式（16）的演化过程可以获得相对应的消费决策函数模拟值。

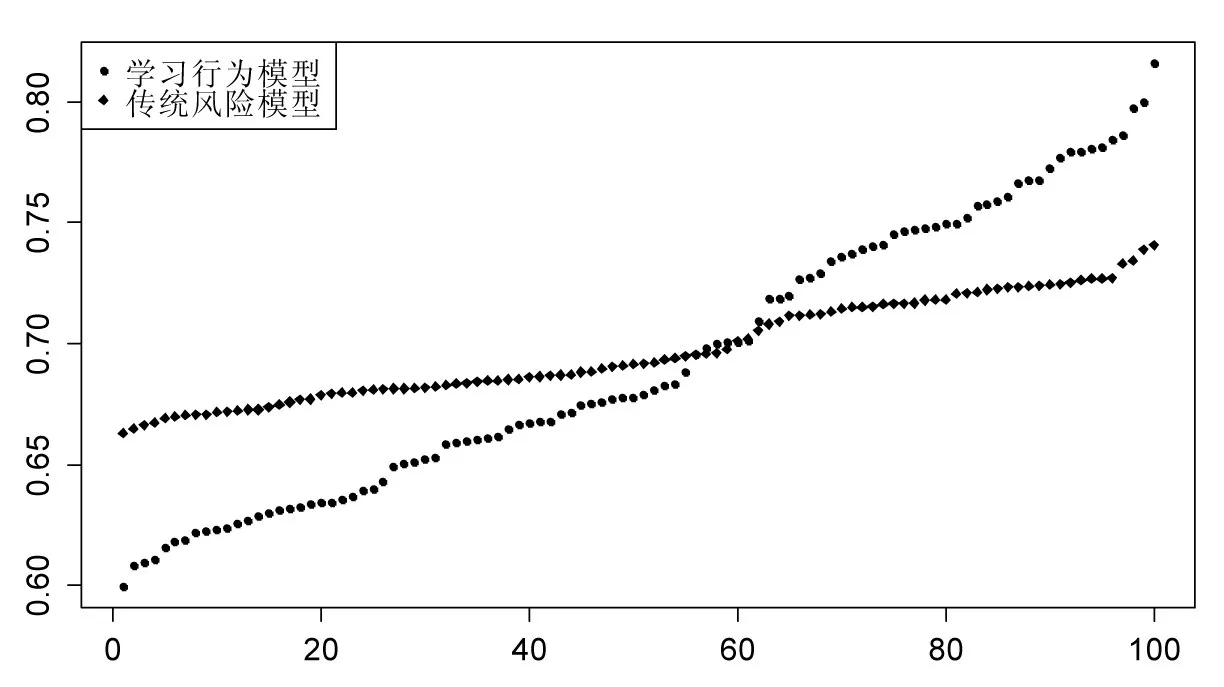
图2 市场学习行为对消费决策的影响

图2给出了分别基于式（11）和式（16），在最优消费决策下模拟计算得到的消费流。为了消除随机扰动的影响，具体做法是每次模拟生成1000个样本，然后对这些样本计算参数均值，共模拟100次。可以发现风险度量模型中的消费流贴近0.7上下波动。而在考虑学习行为的贝叶斯决策模型中，开始的消费偏低，这反映了消费者在初期获取的信息有限，对真实参数θ的信念仍需不断更新，从而提高了预防性储蓄。不过随后消费将逐渐上升，甚至超过理性预期假设下的消费量。这是因为消费者在初期积累了更多的财富，获得更多的利息收入，而且随着学习过程积累的信息，对参数的信念更加可靠，从而逐渐提高了消费量。

3 结论

本文在贝叶斯框架下构建了考虑市场学习行为的决策模型，并以消费-储蓄模型为例说明了学习行为对决策的影响。通过学习模型的构建和应用，可以发现一些决策问题不再是简单的模型求解过程，外部的约束和自身的学习不断交互进行，在贝叶斯框架下能够得到较为灵活的处理。而且对于传统模型中难以描述的市场现象，考虑市场学习行为后构建的贝叶斯模型在一定程度上能够给出解释，这值得引起对传统风险度量方法的反思，进而不断完善统计决策方法。

值得说明的是，如果在建模时假定决策者的信念与抽样估计值一致，但实际上并不相符，将会导致模型残差出现序列相关及异方差等问题，表现为消费者会有更加激进的预防储蓄行为。另外在参数独立同分布的假定下，收益由真实参数生成，如果不知道真实值的决策者在主观上认为未来的收益会出现更高的波动性，这将导致决策者担心收入过程可能会出现结构转变等现象，动摇了其从过去收入数据获得经验的信念。这些问题会对模型的内生变量造成显著影响，是未来值得进一步研究的方向。

[1]Christiano J,Motto R,Rostagno M.Risk Shocks[J].American Eco⁃nomic Review,2014,104（2）.

[2]Pástor L,Veronesi P.Learning in Financial Markets[J].Annual Re⁃view of Financial Economics,2009,1（1）.

[3]Hansen L.Sargent T.Fragile Beliefs and the Price of Uncertainty[J].Quantitative Economics,2010,1（1）.

[4]Bekaert G,Hoerova M,Duca L.Risk,Uncertainty,and Monetary Poli⁃cy[J].Journal of Monetary Economics,2013,60（3）.

[5]Blanchard O,Ariccia G,Mauro P.Rethinking Macroeconomic Policy[J].Journal of Money Credit and Banking,2010,42（1）.

[6]徐元栋,黄登仕,刘思峰.奈特不确定性下的行为决策理论研究综述[J].系统管理学报,2008,17（5）.

[7]高金窑.奈特不确定性与非流动资产定价:理论与实证[J].经济研究,2013,（10）.

[8]Guy T,Karny M,Wolpert D.Decision Making:Uncertainty,Imperfec⁃tion,Deliberation and Scalability[M].New York:Springer,2015.

[9]Machina M,Viscusi W.Handbook of the Economics of Risk and Un⁃certainty[M].Oxford:North Holland,2014.

[10]Weitzman M.Subjective Expectations and Asset-return Puzzles[J].American Economic Review,2007,97（4）.

[11]Blanchard O,Romer D,Spence M,et al.In the Wake of the Crisis:Leading Economists Reassess Economic Policy[M].Cambridge:MIT Press,2014.

[12]Galati G,Moessner R.Macroprudential Policy.A Literature Review[J].Journal of Economic Surveys,2013,27（5）.

[13]Bloom N.The Impact of Uncertainty Shocks[J].Econometrica,2009,77（2）.

[14]Al-Najjar N,Weinstein J.A Bayesian Model ofKnightianUncertainty[R].ReiheÖkonomie/Economics Series,InstitutfürHöhereStudien（IHS）,No.300,2013.