一种粮粒图像快速重构方法
2018-01-09许德刚廉飞宇
许德刚 ,廉飞宇 *
(河南工业大学 1.粮食信息处理与控制教育部重点实验室;2.粮食光电探测与控制河南省重点实验室;3.信息科学与工程学院,河南 郑州 450001)
一种粮粒图像快速重构方法
许德刚1,2,3,廉飞宇1,2,3*
(河南工业大学 1.粮食信息处理与控制教育部重点实验室;2.粮食光电探测与控制河南省重点实验室;3.信息科学与工程学院,河南 郑州 450001)
针对粮情实时检测过程中图像清晰度下降,给后续分析造成困难的问题,提出一种新的图像重建记忆梯度追踪(MGP)算法,用于减少压缩感知方向追踪算法的重构时间并提高重构精度。该算法结合正则化正交匹配追踪(ROMP)的元胞生成方法,利用非单调非精确阿米霍线搜索方法确定迭代步长,利用MGP算法锁定搜索方向,可以在保证图像重构精度的同时,缩短重构时间。对原有MGP算法的方向参数公式进行了推导和改进,得到了效率更高的计算公式,使得算法的运行时间较共轭梯度追踪算法节省30%,并可精确重构二维粮粒图像信号。本算法的运行结果表明,在相同硬件平台下,其二维粮粒图像信号的重构性能优于其他的同类重构算法。
粮粒检测;压缩感知;方向追踪;记忆梯度;图像重构
0 引言
我国是粮食生产、流通、消费大国,随着人们生活水平的提高,粮食供求的主要矛盾已从数量上的欠缺转为质量上的担忧。当前,粮食品质检测还停留在利用传统手段人工观测的水平,有关品质指标的确定缺乏客观性和科学性,而且无法满足快速检测的要求,给粮食的分级利用造成了困难。
目前,将图像处理技术引入粮食颗粒外观品质检测,成为了国内外的研究热点[1]。在实际应用中,粮食收储环境复杂,外部噪声和干扰很强,对粮粒成像质量造成影响,为图像的后续分析带来困难,因此粮粒图像的快速恢复重建十分重要。近年来,压缩感知(CS)理论受到广泛关注,它突破了传统的Naquist定理的限制,带来了信号获取方式的变革。在CS中,信号的恢复重建是一个基本的关键问题,其算法应当能够对信号进行精确重构,这实质上可归结为一个优化问题的求解过程[2-3]。因此,将压缩感知(CS)理论方法应用于粮粒图像重构,提升成像质量,对于促进粮食颗粒品质检测技术发展以及应用领域拓展有重要的实际意义。
在目前的压缩感知重建算法中,贪婪算法是应用最为广泛的一类,其要点有两个:匹配追踪和方向追踪。在匹配追踪中,通常采用正交匹配追踪(orthogonal matching pursuit,MP)算法。该算法继承了匹配追踪(matching pursuit,MP)算法的元胞生成方法,并在选中元胞后进行正交化。但该算法对于高维观测矩阵需要大量投影计算,时间复杂度较高,因而一系列改进算法又被提了出来,如正则化正交匹配追踪(regularized OMP)[4]、分段正交匹配追踪(blockOMP)等。在方向追踪中,常用的算法是基于贪婪算法的方向追踪算法[5],主要包括:梯度追踪法(gradientpursuit,GP)、近似共轭梯度追踪法(approximate conjugate gradient pursuit,ACGP)、 共轭梯度追踪法(conjugate gradient pursuit, CGP)、谱投影梯度追踪法(spectral projected gradient pursuit,SPGP)[6]和分段弱阈值共轭梯度追踪法[7]等。
方向追踪法和匹配追踪法的元胞生成方式相同,不同之处在于:方向追踪法采用的是共轭梯度、负梯度方向作为搜索方向进行求解,而不是采用匹配追踪法中较为耗时的最小二乘法进行求解,但其缺陷是重建精度不够高。作者针对这一问题,在正则化正交匹配追踪基础上,采用非单调记忆梯度的方向更新机制,提出一种新的记忆梯度追踪算法,该算法克服了共轭梯度追踪法计算量大且收敛速度慢的问题。
1 元胞生成方法
对于长度为N的一维信号xϵRN,若其不为零的元素个数为S且S<N,则称信号是稀疏的。由压缩感知理论,对于随机测量矩阵 AϵRM×N,当 M<N且满足一定条件时,通过压缩感知可得到长度为M的一维观测信号y,且有如下关系:

称测量矩阵A的列向量Ai为元胞。根据文献[8],信号x通过M个在测量矩阵A上的非相干投影,即可实现重建。本文的元胞生成方法采用正则化正交匹配追踪算法[4]。该方法首先进行元胞的第一次筛选,方法是通过求矩阵A中各个元胞与余量r的内积(Ai, )
r的绝对值来求取相关系数u,即:

通过此方法筛选出S个元胞,并将其索引值存到侯选集J中。然后进行第2次筛选,即对筛选出的元胞先进行正则化,根据式(2)将第1次筛选出的元胞的系数进行分组,生成系数值最大的一组元胞,并将其序号存入侯选集J0中,J0在文中又称为初次侯选集。
选择正则化正交匹配追踪算法的目的在于避免采用最小二乘法进行信号逼近带来的算法复杂性问题,其算法的简单流程为:
(1)初始化参数。初始余量r0=y,迭代次数n=1,估计信号稀疏度为S,索引值集合A=φ,J=φ;
(2)根据式(2)计算相关系数u;
(3)对u降序排列,取前S个最大值,更新 J中对应的索引值;
(4) 正则化。筛选满足|u(i)|≤2|u(j)|,i,jϵJ 的元胞,将其索引值存入集合J0中;
(5) 更新支撑集 AΛ,其中 Λ=Λ∪J0。
2 非单调记忆梯度算法
记忆梯度法不用矩阵的存储和计算,是改进的共轭梯度法,适用于无约束优化问题的求解[9],算法简单,是常用的最优化方法之一,常采用如下迭代式:

式中:xn为估计值;αn为搜索步长;dn为更新方向。
CGP算法采用共轭梯度方向[5]确定更新方向,而在记忆梯度法中,则是由前一迭代点的搜索方向dn-1和当前迭代点的反梯度方向-gn组合成搜索方向,这种组合不仅利用了当前点的方向信息,也利用了前一迭代点的方向信息,提高了参数选择灵活性,因而使收敛更为稳定[9]。
下面利用梯度追踪法求解式(1):
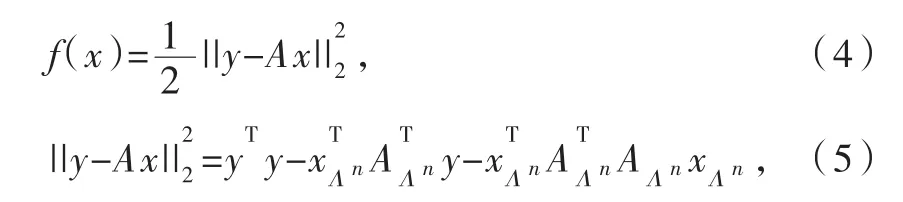
式中:Λn为在n次迭代时,选取元胞下标的集合,AΛn为Λn对应的元胞组成的矩阵。

将式(4)代入式(6),

重建图像时,GP算法有两个问题需要解决:一是如何确定循环步长,二是如何确定前一迭代点负梯度的方向。设gn为梯度函数,则:

而更新方向的计算如下:
(1)当||gn||=0,停止迭代,否则继续;
(2)确定搜索方向:

在CGP算法中,最优步长的求法依赖单调精确搜索算法[12],如下式所示。

式中:琢可根据文献[11]确定。
求解无约束优化问题时,单调精确算法的效率较低,甚至会有锯齿现象[12],采用非单调搜索算法[13],解决了一些缺点,使算法的整体性能有了很大的改善。本文采用文献[11]的方法,它是一种非单调改进Armijo线搜索,具有运算量少、速度快、易于实现的优点。
3 记忆梯度追踪算法的改进
方向追踪算法的元胞生成方法与MP算法是相同的,不同之处是它的余差更新方式是记忆梯度算法,而不是最小二乘算法,从而更容易得到全局最优解。
在记忆梯度算法中,搜索方向中的参数βn,根据文献[14],由式(3)可得:

记忆梯度法的算法流程如图1所示。算法首先进行初始化:r0=y,索引集 J=Ø,I0=Ø,迭代变量 n=1;然后重复以下步骤:

图1 记忆梯度算法流程图Fig.1 The flow diagram of the memory gradient algorithm
(1)利用ROMP算法得到投影系数值μ,进行元胞选择,得到候选元胞集,进行正则化,得到最大能量子集,即
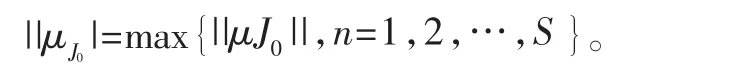
(2)采用非单调记忆梯度法求解 xn,dn,rn,步骤如下:①计算梯度;②计算方向,将本节推导的 βn带入式(9)求得③计算步长;④求的近似解;⑤观测余量信号更新,即
重复步骤(1)和步骤(2)直到满足迭代停止条件。最后输出重构信号的元胞支撑集
上述MPG算法的时间复杂度主要由两个方面决定,一是元胞的选择,需要计算ATr,其时间复杂度记为O(A),和正则化元胞的二次筛选,其时间复杂度为O(KMN),二是更新方向和步长的计算,时间复杂度分别为 O(A)和O(M)。从总体上看,MGP算法的时间复杂度与CGP算法处于相同级别上。
通过上述流程,本文的记忆梯度算法与其他算法相比,其优势为:(1)元胞生成方法采用方向追踪与正则化正交匹配追踪选择相结合,提高了每次迭代的速率;(2)采用非单调线搜索,减少了步长计算的时间,提高了收敛效率,避免了锯齿现象的发生。
4 测试结果和性能分析
首先通过重构一个一维稀疏信号,比较本文算法与传统的梯度追踪算法、正交匹配算法在时间复杂性、相对误差方面的性能;然后通过重构一个二维粮粒图像信号,比较本文算法与上述两种算法在时间复杂性、相对误差方面的性能。
对相对误差的定义[15]:
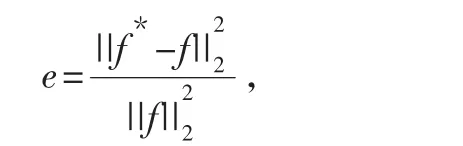
式中:f*为原始信号,f为重构信号,e为相对误差,e越小表明精度越高。
本文算法及其他算法的比较均在Windows 7系统下运行,硬件配置为:CPU2GHz,内存4GBDDR2,显卡支持DirectX 9,硬盘 500 GB。仿真软件使用的是MATLAB R2013a。仿真参数如表1所示。

表1 仿真参数Table 1 Simulation parameters
4.1 一维稀疏信号的重构性能
对本文的改进记忆梯度追踪算法、传统梯度追踪算法、近似共轭梯度追踪算法以及正则化正交匹配追踪算法进行了重构误差和运算时间上的比较。考虑到信号中通常含有高斯噪声,在高斯噪声方差为σ2时,各算法对一维稀疏信号的重构精度和时间如表2所示。
由表2可知,4种算法的运算时间在一个数量级上。当σ2=1×10-3时,4种算法的相对误差均较小,随着σ2增大,正则化正交匹配追踪和改进型记忆梯度追踪算法的时间逐渐延长,当σ2=5×10-3时,这两种算法所需时间较短。总体上看,正则化正交匹配追踪算法对高斯噪声比较敏感,而改进型记忆梯度追踪算法则稳定性较好,抗干扰性能优于其他算法。由图2可见,从重建效果上看,改进型记忆梯度追踪算法对一维稀疏信号的重构质量和运算时间均优于近似共轭梯度追踪算法和正则化正交匹配追踪算法。

表2 一维信号的重建时间和重建误差Table 2 The reconstruction time and error of one-dimensional signal


图2 一维稀疏信号的重构性能(稀疏度,方差0.001)Fig.2 The reconstruction performance of one-dimensional sparse signal(sparsenes,variance:0.001)
4.2 二维粮粒图像信号的重构性能
改进型记忆梯度追踪算法是一种对稀疏信号进行精确重构的算法,在用于对粮粒图像的重构时,首先需要将粮粒图像表示为稀疏信号。常用方法有小波变换法、快速傅里叶变换法等。本文采用小波变换法。重构粮粒图像信号的流程为:①将高斯随机矩阵与小波基相乘,得到测量矩阵;②利用测量矩阵得到粮粒图像信号的测量值;③利用改进型记忆梯度追踪算法,重构出粮粒图像的小波系数;④通过小波反变换重构出原始粮粒图像。
图3为采用M/N=0.5的采样率,4种算法的粮粒图像重构效果,相应的峰值信噪比如表3所示。图3中的粮粒图像来源于河南工业大学粮食信息处理与控制教育部重点实验室,像素尺寸均为512×512。


图3 不同算法对粮粒图像的重建效果Fig.3 The reconstruction effect of the grain images of four algorithms

表3 不同算法图像重建峰值信噪比Table 3 The peak signal to noise ratio of four algorithms dB
由图3可以看出,改进型记忆梯度追踪算法的峰值信噪比最大,且算法运行时间比近似共轭梯度追踪算法减少30%。当M/N=0.5时,具有相对更高的重构精度。
图4表明了采样率对粮粒图像重构的影响。由图4可知,4种算法随着测量次数的增加,粮粒图像的重构质量均有所提高。当采样率小于0.2时,4种算法的重构效果相差不大,但当采样率大于0.2时,改进型记忆梯度追踪算法的峰值信噪比高于其他算法,因而具有更好的特性。虽然正则化正交匹配追踪具有与记忆梯度追踪相同的元胞生成方法,但正则化正交匹配追踪算法的图像重构质量最差。这是因为本文改进型记忆梯度追踪算法采用的是不同方向的步长更新机制,因而使其性能得到大幅度提高。

图4 不同采样率的粮粒图像重建效果Fig.4 The reconstruction effect of the grain images of four sampling frequency
5 结论
针对粮情实时监测过程中图像清晰度不足造成识别困难的问题,提出了一种新的图像重构算法——改进型记忆梯度追踪算法(MGP),用于提高粮食品质在线监测中粮粒图像的恢复效果。该算法吸收正则化正交匹配追踪算法的元胞吸收方法,结合方向梯度算法,采用记忆梯度最终确定搜索方向,采用非单调非精确Armijo线搜索准则确定补偿,使得在提高信号重构精确度的同时,缩短了重构时间。仿真结果表明,本算法可显著改善粮粒图像和其他实时粮情监测图像的重构质量。算法存在的问题是,在时间复杂度上还没有显著的优化,另外,目前还没有考虑彩色图像的重构,需要在今后的工作中做进一步的研究。
[1] 周志强,成军虎,潘石.基于计算机视觉的稻米品质评价研究进展[J].河南工业大学学报(自然科学版), 2012, 33(6):95-100.
[2] 周燕,曾凡智.基于二维压缩感知和分层特征的图像检索算法[J].电子学报,2016,44(2):453-460.
[3] 刘芳,武娇,杨淑媛,等.结构化压缩感知进展[J].自动化学报,2013,39(12):1980-1995.
[4] 刘哲,张鹤妮,张永亮,等.基于弱选择正则化正交匹配追踪的图像重构算法[J].光子学报,2012,41(10):1217-1221.
[5] 刘盼盼.压缩感知中梯度追踪算法的研究[D].南京:南京邮电大学,2015.
[6] 李志林,陈后金,姚畅,等.基于谱投影梯度追踪的压缩感知重建算法[J].自动化学报,2012,38(7):1218-1223.
[7] BLUMENSATH T,DAVIES M E.Gradient pursuits[J].IEEE Transactions on Signal Processing, 2008, 56(6):2370-2382.
[8] 方红,杨海蓉.贪婪算法与压缩感知理论[J].自动化学报,2011,37(12):1413-1421.
[9] 时贞军.无约束优化的超记忆梯度算法[J].工程数学学报,2000,17(2):99-104.
[10] JIAN B J,ZENG F Y,TANG C M.A generalized super-memory gradient projection method of strongly sub-feasible directions with strong convergence for nonlinear inequality constrained optimization[J].Computers and Mathematics with Applications, 2007,54(4):507-524.
[11] 汤京永,董丽.一类新的记忆梯度法及其收敛性[J].工程数学学报,2010,27(4):637-642.
[12] 汤京永,董丽.非单调线搜索下的记忆梯度法及其全局收敛性[J].四川师范大学学报(自然科学版),2010,33(1):32-35.
[13] 汤京永,贺国平,董丽.一类新的求解无约束优化问题的记忆梯度法[J].数学杂志,2011,31(2):362-368.
[14] MALLAT S,陈刚,张亶,等.应用数学和信号处理相遇[J].高校应用数学学报, 1999,14(3):350-366.
[15] 郭强,孙鹏,赵迎春,等.基于记忆梯度追踪的高效稀疏跟踪算法[J].计算机辅助设计与图形学学报,2016,28(4):565-571.
A FAST METHOD FOR IMAGE RECONSTRUCTION OF GRAIN KERNELS
XU Degang1,2,3,LIAN Feiyu1,2,3
(Henan University of Technology,1.Key Laboratory of Ministry of Education for Grain Information Processing and Control;2.Key Laboratory of Henan Province for Grain Photodetection and Control;3.School of Information Science and Engineering,Zhengzhou 450001,China)
For the problem that charity of images decreasing in the real-time monitoring of grain kernels situation, which causing difficulties for the subsequent analysis, a new image reconstruction method based on memory gradient pursuit (MGP)algorithm was proposed used to reduce the reconstruction time and improve the reconstruction precision of the compressed sensing direction tracking algorithm. The algorithm combined the cell generation method of regularized orthogonal matching pursuit,utilizing non-monotonic and un-precise Armijo linear search to determine step size, and using MGP to lock search direction, which could reduce reconstruction time under satisfactory reconstruction precision. In this study,the former formula of direction parameters for MGP was inferred and improved, and the formula with higher efficiency was afforded, which made the proposed algorithm to save time 30% compared with Conjugate gradient tracking algorithm,and could also reconstruct two-dimensional images of grian precisely. Experimental results indicated that the method proposed in the present study had better reconstruction performance of grain images than other algorithms under the same test conditions.
grain kernels detection;compressive sensing;direction tracking;memory gradient method;image reconstruction
TP391.9
B
1673-2383(2017)06-0074-06
http://kns.cnki.net/kcms/detail/41.1378.N.20171226.1723.026.html
网络出版时间:2017-12-26 17:24:10
2017-03-17
河南省科技发展计划项目(162102310405);河南省基础与前沿计划项目 (152300410079);国家重点研发计划项目(2017YFD0401003)
许德刚(1978—),男,河南周口人,副教授,研究方向为智能优化算法、图像处理。
*通信作者
