空心钢锭凝固过程缺陷的模拟研究

张 博，朱 花,赵晓东,何文武,陈慧琴

(太原科技大学材料科学与工程学院，太原 030024)

空心钢锭凝固过程缺陷的模拟研究

张 博，朱 花,赵晓东,何文武,陈慧琴

(太原科技大学材料科学与工程学院，太原 030024)

利用有限元软件ProCAST对65t空心钢锭底注式凝固过程进行了数值模拟。根据实验条件和实验结果，分析确定了最终凝固位置在距离内壁35%壁厚处时的内壁界面换热系数为400 W/m2·K.采用相同的锭型、浇注方式和边界条件对4.2 t Mn18Cr18N空心钢锭进行了模拟研究，分析了不同浇注温度和浇注速度下的凝固过程。结果表明，在浇注温度为1 415 ℃，浇注速度为25 kg/s 条件下，实现了顺序凝固，最终凝固位置在冒口内，钢锭内没有出现宏观缩孔疏松，冒口根部下方靠近钢锭内壁处存在条状的显微缩松。

空心钢锭；数值模拟；凝固；缩孔缩松

传统的空心钢锭是由实心钢锭经过多道机械加工工序得到的，例如镦粗、冲孔等。传统制造技术存在许多弊端，例如能耗高、工序繁琐、材料利用率低、生产周期长等。为了解决这些弊端，空心钢锭制造技术应运而生。法国、日本、德国等多个国家在这一技术上取得了突出的成绩。空心钢锭制造技术与传统制造技术相比具有缩短工艺流程、降低生产成本以及提高生产效率等一系列的优势[1-4]。

早期由于技术手段的不发达，主要采取实物解剖的方法对钢锭进行研究，虽然结果准确，但是存在费用高、浪费大、实验周期长等缺点，阻碍了钢锭的研发生产。计算机技术的飞速发展，使得模拟仿真技术成为研究钢锭质量与性能的一种全新手段，如今该技术已基本成熟，进入了实用化阶段。模拟仿真技术可以对多种类型的模型进行计算和分析，预测凝固结束后钢锭内部是否产生缺陷以及缺陷的形貌和位置，预测铸件的显微组织等[5-7]。

空心钢锭制造技术的关键是芯子的设计，芯子主要有两种：双套筒式和单套筒式，本文采用由日本川崎制铁公司发明的双套筒式芯子进行模拟计算[8-10]。

1 65 t空心钢锭凝固过程模拟及内壁界面换热系数的确定

1.1 有限元模型的建立

采用底注双套筒式的浇注系统对空心钢锭进行浇注。底注式浇注可以使充型过程中金属液上升平稳，避免金属液发生激溅、氧化等缺陷。65 t空心钢锭高2 410 mm，内径700 mm，顶部外径2 375 mm，底部外径2170 mm.利用三维建模软件建模后直接导入铸造模拟软件ProCAST中进行网格的划分[11]，得到2D四边形网格单元47 048个，3D六面体网格单元626 624个。

1.2 浇注工艺参数

底注式的浇注系统较为复杂，所以设计合理的浇注工艺参数是十分必要的，如果参数设计的不合理，会在充型过程中产生断流，卷气等现象，在一定程度上降低空心钢锭的质量[12]。

根据文献[3]，65 t空心钢锭的材质是20MnSi.其液相线温度为1 501 ℃，固相线温度为1 110 ℃.浇注温度为1 548 ℃.浇注系统采用两个内浇道，经过计算可以得到直浇道、横浇道和两个内浇道的尺寸分别为D直=86 mm、D横=86 mm、D内=68 mm.浇注速度为300 mm/min，这里的浇注速度是指型腔内钢液的上升速度。浇注时间是482 s.钢锭模初始温度为200 ℃，环境温度为20℃.采用保温冒口，在冒口外加保温层，保温层厚度为20 mm.耐火材料采用铬矿砂加树脂，为保证芯子的强度，耐火材料的厚度为30 mm.钢锭模与空气之间采用空冷。重力加速度为g=9.8 m/s2.

1.3 内壁界面换热系数对钢锭最终凝固位置的影响

在空心钢锭凝固过程中，钢锭内外壁的冷却条件是不同的。其中外壁的冷却条件随空心钢锭尺寸的变化影响较小，而内壁的冷却条件则取决于芯子的冷却条件。将外壁换热系数设为定值，选取不同内壁换热系数，分析内壁换热系数对空心钢锭最终凝固位置的影响。用冒口根部处最终凝固位置的分数值(最终凝固位置至内壁的距离/钢锭厚度)来衡量内壁换热系数对最终凝固位置的影响。设置钢液与钢锭模之间的换热系数为1 000 W/m2·K；钢液与保温层之间的换热系数为50 W/m2·K；钢液与底部砂模之间的换热系数为300 W/m2·K；内壁换热系数分别取100 W/m2·K、200 W/m2·K、300 W/m2·K、400 W/m2·K、500 W/m2·K.数值模拟结果如表1所示。从表1中可以看出，随着内壁界面换热系数的增大，最终凝固位置逐渐远离内壁，向钢锭壁厚中部靠近。

钢水采用真空炉冶炼。凝固结束后先脱模，然后取出芯子的内套筒。在切割冒口后对冒口根部进行酸硫印及酸洗，检查冒口根部处的最终凝固位置，明显地观察到当内壁换热系数为400 W/m2·K时，65 t空心钢锭最终凝固位置位于冒口根部下方距离内壁的35%壁厚处，模拟结果与实际结果吻合较好。

表1 最终凝固位置的模拟结果

Tab.1 The simulation results of the final solidification positions

内壁界面换热系数/W/m2·K最终凝固位置至内壁的距离/mm最终凝固位置距内壁的壁厚百分数10025932．6%20026333．1%30027434．4%40027935．0%50030338．2%

图1为内壁界面换热系数为400 W/m2·K时，65 t空心钢锭不同时刻充型凝固状态图。由图中可看出，在空心钢锭的充型过程中，钢液液面上升平稳，没有发生激溅等较大的起伏现象。金属液在478 s时基本将整个型腔充满，与计算所得的482 s的误差在合理的误差范围内，说明各浇注工艺参数的设定是合理的。

空心钢锭理想状态下的凝固顺序是内外壁向中心、由下向上的逐层凝固，最终凝固位置位于钢锭的中上部或冒口内。从图1中可以看到，轴向上由空心钢锭底部向冒口处推进。由于内外壁的换热系数不同，壁厚剖面内温度场对称轴靠近内壁，即外壁换热系数较大，外壁冷却较内壁快，即径向上由钢锭的内外壁向钢锭中部推进，最终凝固位置位于靠近内壁的冒口内。

2 Mn18Cr18N空心钢锭凝固过程模拟分析

2.1 有限元模型的建立

Mn18Cr18N空心钢锭的尺寸图与网格划分半剖面图如图2所示。建模后导入ProCAST软件中进行网格划分，得到2D四边形网格63 952个，3D六面体网格655 363个。钢锭模进行预热，初始温度为200℃.环境温度20 ℃.冒口采用保温板保温，保温层厚度为10 mm.耐火材料选用树脂砂，厚度为20 mm.其他边界条件均采用与最终凝固位置为35%时的65 t空心钢锭相同的设置。

图1 65 t空心钢锭不同时刻充型凝固状态图

Fig.1 The filling and solidification states at different times of the 65 t hollow ingot

(a)尺寸图 (b)网格划分图

图2 Mn18Cr18N空心钢锭尺寸和网格划分图

Fig.2 The size and the FE model of Mn18Cr18N hollow ingot

2.2 浇注工艺参数的确定

Mn18Cr18N护环材料的化学成分如表2所示。液相线温度为1 385 ℃，固相线温度为1 170 ℃.经过计算可得到直浇道、横浇道、两个内浇道的尺寸分别为D直=60 mm、D横=60 mm、D内=48 mm.

2.3 缩孔缩松判据的理论基础

高温合金在凝固过程中会发生体积收缩现象，最终凝固部位有可能因得不到钢液的及时补充而产生的宏观空隙缺陷，即缩孔。若孔洞细小而分散，则又称缩松(疏松)。

铸件因凝固收缩产生的缺陷不仅仅有宏观的缩孔缩松，还会在枝晶间产生显微缩松。这里采用Niyama判据来对显微缩松出现的可能性进行模拟预测。Niyama判据是一种基于枝晶间显微缩松的预测判据，可以较准确的预测显微缩松可能产生的位置和分布情况。表达式如下所示。

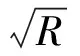
(1)

表2 Mn18Cr18N的化学成分(质量分数%)

Tab.2 Chemical composition of Mn18Cr18N (mass fraction%)

化学成分CMnCrNNiSiCuPS质量分数0．0719．2120．10．640．140．470．070．0120．07

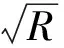
文献[15]中根据达西定律和枝晶间的渗流补缩理论推导出Niyama判据计算公式：

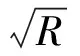
(2)

由公式(2)可以看出，Niyama判据是结合糊状区枝晶的生长机制与渗流补缩理论推导出来的，其实质是在凝固过程中产生于枝晶间的显微缩松，即在凝固前沿糊状区域内，由于枝晶臂闭合生长后形成的微小尺度孔洞。所以从理论上讲，Niyama准则是一种用于判断枝晶间显微缩松的预测判据，其值的大小主要表现显微缩松的倾向性。

2.4 凝固过程分析

浇注时间可以用经验公式计算得到：

τ=Amn

(3)

式中τ是浇注时间，s；m是铸件或浇注金属的质量，kg；A，n是经验系数，其取值范围分别选取1.5～2.35, 0.5时最为合适。

浇注速度v可以用每秒钟进入型腔的钢液量进行表示，用式(4)计算可得：

v=M/τ

(4)

式中M是铸件的质量，kg；τ是浇注时间，s[16].

2.4.1 不同浇注温度下的凝固过程

采用底注法对钢锭进行浇注时，过热度不宜选取过高，Mn18Cr18N的液相线温度为1 385 ℃.根据过热度高出液相线30～50 ℃的合理范围，分别选取浇注温度为1 415 ℃、1 425 ℃、1 435 ℃对凝固过程进行模拟计算，模拟结束后空心钢锭内部显微缩松的分布情况如图3所示。

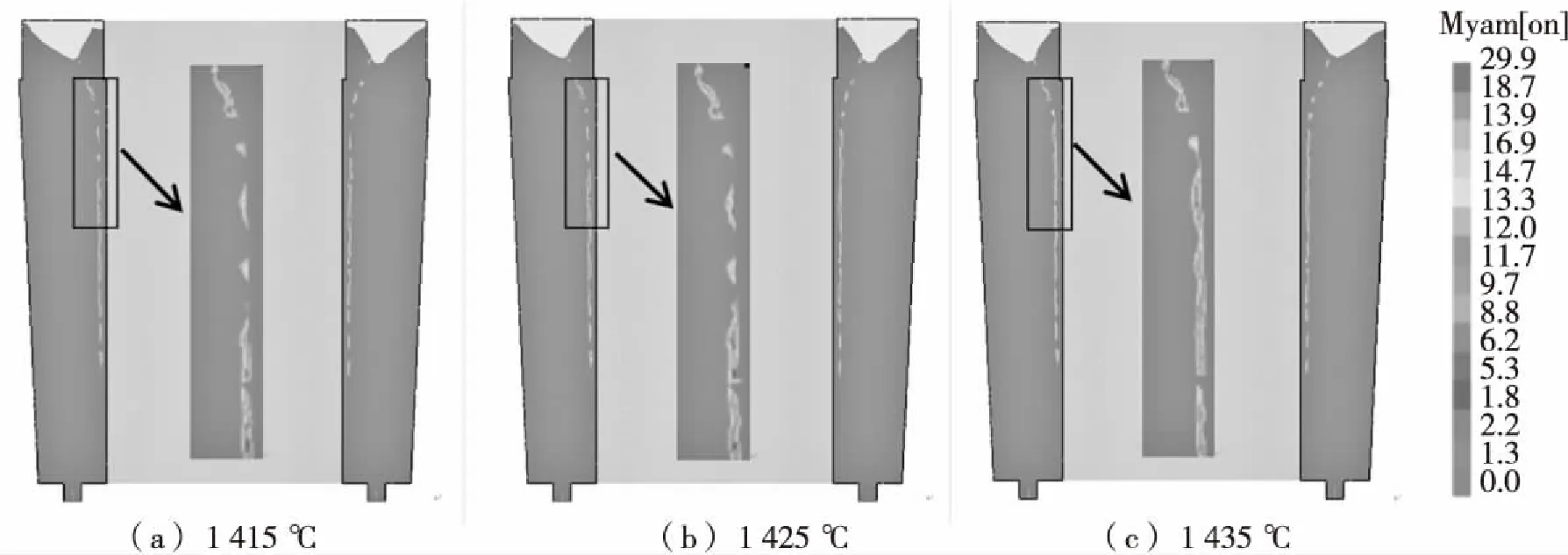
图3 不同浇注温度下模拟的显微缩松结果

Fig.3 Micro-porosities results of the simulation at different pouring temperatures

浇注温度对合金流动性的影响显著，提高浇注温度有利于提高金属的流动性。但会加大缩孔缩松缺陷的程度，造成晶粒粗大等现象；而浇注温度过低会造成浇不足、冷隔、夹砂等现象。所以设置合适的浇注温度十分必要。从图3中可以看出，空心钢锭凝固后，在冒口根部下方靠近内壁处会出现长条状的缩松区域，一直延伸至钢锭下部。这是因为凝固前沿的枝晶互相搭接成固相骨架，进行闭合生长，闭合区域内的残余液相构成一个个孤立的微小熔池，这些液相在转变成固相的过程中会造成体积损失，若此时得不到外部金属液的及时补充或不能进行补充时，就会产生枝晶间的显微缩松。在对显微缩松的严重程度进行比较时，既可以通过Niyama数值进行比较，也可以对显微缩松区域的长度或宽度进行测量，通过长度值或宽度值来综合衡量显微缩松的严重程度。由图可以看到，随着浇注温度的升高，Niyama数值逐渐减小，说明产生显微缩松的倾向性逐渐增大。但显微缩松区域的长度逐渐减小，长度分别约为689 mm、688 mm、661 mm.综合考虑显微缩松程度呈逐渐增大趋势，所以浇注时可取较低的浇注温度为1 415 ℃.

2.4.2 不同浇注速度下的凝固过程

经过式(4)的计算可得到浇注速度为33 kg/s，这里当浇注温度为1 415 ℃时，分别设置浇注速度为25 kg/s、33 kg/s、45 kg/s对空心钢锭凝固过程进行模拟，模拟结果如图4所示。

图4 不同浇注速度下模拟的显微缩松结果

Fig.4 Micro-porosities results of the simulation at different pouring velocities

选用较小的浇注速度的优点是充型过程中金属液上升平稳，一直保持水平状态直到充型结束，基本上不存在卷气现象。但是在直浇道中，由于金属液下降会受到重力加速度的影响，上下两端的金属液流动速度之间存在较大差值，会发生液体分离现象，造成浇不满等缺陷。选用较大的浇注速度可以减轻甚至避免上述的液体分离现象，但过快流入型腔的金属液会与型腔内壁产生强烈碰撞，可能使型壁破损产生砂眼，同时也会增大卷气的倾向[17]。从图4中可以看到，空心钢锭冒口根部下方靠近内壁处出现了一定的显微缩松。随着浇注速度的增大，Niyama数值逐渐减小，说明产生显微缩松的倾向性逐渐增大。三种不同浇注速度下显微缩松区域的长度相差不大，均约为688 mm，但区域宽度有所增加，分别约为44 mm、46 mm和48 mm.结合上述两种判断可以得到，显微缩松的程度随着浇注速度的增大呈现增大的趋势。所以，可以选取较低的浇注速度为25 kg/s.

综上所述，在对Mn18Cr18N空心钢锭进行浇注参数设计时，可以采用“低温慢注”工艺，即浇注温度为1 415 ℃，浇注速度为25 kg/s.

2.4.3 合理浇注工艺参数下的模拟分析

图5为浇注温度为1 415 ℃，浇注速度为25 kg/s时，Mn18Cr18N空心钢锭固相线、宏观缩孔缩松和显微缩松的分布图。

从图5(a)可以看出，随着凝固过程的进行，径向上由内外表面向中心逐渐凝固。但由于钢锭内外壁的冷却条件不同，所以外壁冷却速率大于内壁冷却速率。轴向上由底部逐渐向顶部移动，最终凝固位置位于冒口中，符合顺序凝固的特征。

图5 凝固过程固相线

Fig.5 Fraction solid the solidification process

图5(b)是凝固冷却后宏观缩孔缩松的模拟结果。可以看到，钢锭锭身中不存在宏观缩孔缩松缺陷，缺陷集中在冒口中最后凝固的位置，说明冒口的尺寸设计和保温条件均合理，可以在凝固过程中对钢锭进行有效的补缩。同时由于外壁冷却速率大于内壁冷却速率，宏观缩孔缩松出现在距离内壁大约89 mm处。图5(c)是显微缩松模拟结果。可以看到，空心钢锭凝固后，在冒口根部下方靠近内壁出现条状的显微缩松区域，一直延伸至钢锭下部约1/3处。

在钢锭的凝固过程中出现宏观的缩孔缩松缺陷是不可避免的[18]，可以根据通过设计合理的浇注工艺参数和选择合适的冒口，将缩孔缩松缺陷完全置于冒口内，后期加工时将冒口切除，保证了钢锭锭身内没有宏观的缩孔疏松缺陷。本文采用的护环钢材料Mn18Cr18N奥氏体不锈钢是一种凝固区间较大的合金，这类合金在凝固过程中除了会产生宏观缩孔外，往往还伴随着显微缩松的产生，该种缺陷是不可避免的，不能通过上述方法进行消除，但是可以通过后续的加工工序的压实闭合进行消除，得到致密的锻件。

3 结 论

(1)对65 t空心钢锭进行模拟研究得出，随着内壁界面换热系数的增大，最终凝固位置逐渐靠近钢锭内壁。在内壁界面换热系数为400 W/m2·K时，冒口根部处最终凝固线大约在距离内壁的35%壁厚处，与实际生产中钢锭的最终凝固位置一致。

(2)采用与65 t空心钢锭相同的边界条件，对4.2 t Mn18Cr18N空心钢锭进行模拟研究。结果表明，随着浇注温度升高与浇注速度的增大，空心钢锭冒口根部下方靠近内壁出现条状显微缩松区域，均呈增大趋势。所以采用浇注温度为1 415 ℃，浇注速度为25 kg/s的“低温慢注”的浇注参数较为合理。凝固结束后，空心钢锭锭身内部没有出现宏观缩孔缩松，冒口根部下方靠近内壁处存在条状显微缩松区域，可通过锻造工序消除。

[1] TOMLINSON M, TALAMANTES SILVA J, DAVIES P. The development of hollow ingot technology at Sheffield forge masters international Ltd[J]. Materials Shaping Technology, 2007,24：45-48.

[2] YOSHIHARA IIDA. Development of hollow steel ingot for large forgings[J]. Transaction ISIJ,1982,22:333- 341.

[3] 许天华.空心钢锭的制造技术[J].一重技术,2004(2):28-31

[4] 张向琨,王本一,刘庄.空心钢锭技术文献综述[J].大型铸锻件,2000,88(2): 44-48.

[5] 李昊. 空心钢锭凝固过程的温度场模拟[D]. 沈阳: 沈阳大学, 2015.

[6] 张向琨,石伟,高国峰，等.空心钢锭凝固过程温度场模拟与缩孔、疏松预测[J].铸造,2000,49(6):344- 348.

[7] 许晓浩,郝润元,刘浩.新型冷拔钢管工艺数值模拟机实验研究[J].太原科技大学学报,2015,36(5):353- 356.

[8] 赵长春,赵林,宋雷钧.大型空心钢锭的研制[J].大型铸锻件,1999,86(4): 17-20.

[9] 郭显胜,田丰,杜旋，等.空心钢锭制造技术发展现状[J].大型铸锻件, 2015(2): 12-16.

[10] 陈玉明,宋雷钧,韩学三.空心钢锭制造技术在一重的发展概况及应用前景[J].铸锻件,2002,96(2): 42- 44.

[11] 李日,马军贤,崔启玉.ProCAST从入门到精通[M].北京:中国水利水电出版社,2010.

[12] 丛勉,李隆盛.铸造手册[M].北京:机械工业出版社,1991.

[13] NIYAMA E, UCHIDA T.A method of shrinkage prediction and its application to steel casting practice. AFS Int[J]. Cast Metal,1998,7:52-63.

[14] 崔吉顺,李文珍. 铸件缩孔缩松多种预测判据的应用[J]. 清华大学学报:自然科学版,2001,41(8):5-8.

[15] 贾宝仟,柳百成. 基于枝晶间渗流理论的砂型铸件缩孔缩松判据N=G/R的讨论及应用[J]. 热加工工艺,1996(2):34-36.

[16] 丛勉,李隆盛.铸造手册[M].北京:机械工业出版社,1991.

[17] 仇春荔,陶盼,廖恒成,等.浇注速度对铸件充型过程流场影响的数值模拟[J].铸造, 2007,56(11): 1190-1194.

[18] SUN Xiao-xia,MENG Wen-jun.Design Method of a Vertical Screw Conveyor Based on Taylor-couette-Poiseuille stable helical vortex[J].Advances in Mechanical Engineering,2017,9(7):1-11.

SimulationofSolidificationProcessesofHollowIngots

ZHANG Bo1, ZHU Hua, ZHAO Xiao-dong, HE Wen-wu, CHEN Hui-qin

(School of Materials Science and Engineering, Taiyuan University of Science and Technology, Taiyuan 030024, China)

The bottom filling solidification processes of a hollow ingot with 65 t weight was simulated by ProCAST. The interface heat transfer coefficient between the core and the hollow ingot was analyzed to be 400 W/m2·K based on test conditions and result of the final solidification position located at 35% wall thickness far from the core, the solidification processes of a Mn18Cr18N hollow ingot with 4.2 t weight was also simulated using the same ingot cases and gating system under the same boundary conditions. The influence of pouring temperature and pouring velocity on solidification processes has been analyzed. The results indicate that the sequential solidification and the final solidification position located at riser can be obtained at the pouring temperature of 1 415℃ and the pouring velocity of 25 kg/s. The solidification hollow ingot is free from shrinkage cavities. However, some micro-porosities have been observed in the hollow ingot close to internal surfaces under the root of riser.

hollow ingots， numerical simulation， solidification， shrinkage cavities and micro-porosities

1673-2057(2018)01-0035-07

2016-11-13

国家自然基金重点项目(51575372)

张博(1992-)，女，硕士研究生，主要研究方向为难变型合金锻造理论与技术。

TG111

A

10.3969/j.issn.1673-2057.2018.01.007