改进EMD在轴承故障诊断中的应用

孙永鹏，董增寿

(太原科技大学 电子信息工程学院，太原 030024)

改进EMD在轴承故障诊断中的应用

孙永鹏，董增寿

(太原科技大学 电子信息工程学院，太原 030024)

为解决传统镜像延拓经验模态分解(mirror Empirical Mode Decomposition,简称mirror-EMD)在对信号分解过程中易受随机噪声干扰，易产生虚假固有模态分量(Intrinsic Mode Function,简称IMF)的缺点，论文提出了一种将自适应小波阈值去噪，镜像延拓EMD分解，相关系数法剔除虚假IMF三者相结合的改进EMD方法 (简称wt-mirror-EMD).该方法首先对原始故障信号去噪，然后对去噪后信号镜像延拓EMD分解，得到若干个IMF分量，最后对各IMF分量计算相关系数，对相关系数大的主IMF作频谱分析。仿真信号和实际轴承信号分析均表明，wt-mirror-EMD，该方法相对于传统改进mirror-EMD方法，尤其是当有噪声干扰时，检测结果更加准确。

小波阈值去噪；镜像延拓EMD；轴承；故障诊断

轴承是现代化生产中大型关键设备的重要部件，也是易损件之一[1]。其一个微小的故障往往会导致整个生产现场或者流水线停机，不但会造成巨大的经济损失，而且很可能会直接危害到人的生命安全，因此，提前预知轴承可能发生的故障，防患于未然，对此问题系统分析研究已然迫在眉睫。

近年来，各行各业的科研工作者从没停止过对轴承故障诊断的探索和研究，从最初的听音辨形识别到后来各种时频分析方法的相继应用。听音辨形该方法，其单靠巡检者经验判断，可靠性差。目前，常见的时频分析方法有维格纳分布、短时傅里叶变换、小波变换等[2]，然而，维格纳分布存在交叉项干扰的问题，短时傅立叶变换信号时频窗口固定，无法对信号进行多分辨分析，而小波变换虽为信号添加了灵活可变的时频窗口，可窥探信号任何细节，可是其在分解时小波基函数与分解层数的选取问题具有不确定性，易受科研工作者主观影响，综上，三种分析方法都有不同程度的缺点，不具备自适应性。

经验模态分解(Empirical Mode Decom-position,简称EMD)[3]是一种先进的信号处理方法，尤其针对非平稳信号，它能够根据信号的不同特点选择不同的基函数，从本质上脱离了傅立叶变换的束缚，具有自适应性。该方法已经被广泛应用到结构损伤检测[4]、电力谐波检测[5]、机械故障诊断领域[6]等方方面面。然而，基本EMD分解在使用三次样条插值拟合信号幅值曲线的极大极小值点构造上下包络线时，由于原幅值曲线的端点往往并不是极值点，随着不断的筛分，产生的固有模态分量(Intrinsic Mode Function,简称IMF)失真严重，端点效应由此产生[7]。传统改进EMD采用镜像延拓法(简称mirror-EMD)，该方法先对信号延拓后在分解，得到的IMF分量波形有了明显改善。然而，若把此法放在实际信号中，实际信号往往夹杂着多种噪声干扰，这势必对传统改进EMD分解造成一定的影响，噪声的存在会严重干扰后续对主IMF分量频谱分析的研究[8]，因此，针对这一问题，先对信号做去噪处理，滤除多余干扰，凸显故障特征，接着对其应用镜像延拓法EMD分解，再对分解后的主IMF做相关系数法筛选，这一方法也就应运而生。为便于后续描述，本文将此法简称为wt-mirror-EMD.

1 自适应小波阈值降噪处理

在工程实际中，滚动轴承故障振动信号中往往既有有用信号又同时夹杂着噪声干扰，有用信号往往被淹没在强噪声背景中，因此信号的信噪比低，故障检测难度大，只有有效的滤除噪声，才能获得准确的故障信息。

小波阈值去噪是一种常用的方法，其步骤分为3步[9]:对于任何一个给定信号，首先，经过反复多次实验，确定一个合适的小波基和分解层数，其次，小波分解后会产生一序列高低频系数，对高频细节部分，选取一个恰当的阈值，进行量化去噪处理，最后，将阈值处理后的各层高频细节系数与最后一层低频近似系数重构，重构信号即为去噪信号。

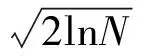
2 基本经验模态分解(EMD)

EMD是一种先进的信号处理方法，它能够根据信号的不同特点自适应选择基函数，彻底脱离了傅里叶变换的束缚，具有自适应性。

其具体分解步骤如下所示[11]：

(1)对于任何一个给定信号x(t)，找出该信号幅值曲线上所有的极大极小值点，将这些极值点用三次样条插值拟合，上下极值点分别构成上下包络线e+(t)与e-(t)，在计算上下包络线的均值，记为m1(t).

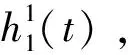
(3)接着，用原信号x(t)减去第一个高频分量c1(t)，重复步骤1，继续筛分，就这样，一个个IMF分量被分解出来，直到最后一个分量幅值曲线变为单调函数为止。

经过上述步骤，一个原始信号就被分解为了若干个固有模态分量与残余量的和，并且是根据信号特征的自适应分解，其公式如下：

(1)

上式中，ci(t)表示从一阶到n阶各阶固有模态分量，而rn(t)代表单调残余量。

3 改进EMD

端点效应是EMD方法的一个核心问题，其产生原因在于在EMD分解步骤1中，要通过三次样条函数插值拟合原信号幅值曲线的极大极小值点，形成上下包络线。而一般情况下，原信号端点处它并不一定是极值点，这样，在第一次筛分时，就会出现拟合误差，刚开始误差可能还小，可是随着筛分步骤的不断循环，第一次筛分误差会累计到第二次，第二次筛分误差会累积到第三次，一着不慎，满盘皆输，最后，IMF分量波形将会严重失真。

针对这个问题，传统改进EMD采用的是镜像延拓法，即mirror-EMD，其顾名思义是先对信号镜像延拓，在对延拓后的信号分解，这种方法相当于把镜子放在原信号幅值曲线对称处，这样，透过镜子的另一端，就会得到另一个原信号，相当于把原信号扩展了一倍，透过镜子，端点处实现了对接，闭合，在对延拓后信号应用步骤1分解，分解完毕，截取需要的那段信号即可。经过实验验证表明，镜像延拓法可以很好的抑制EMD端点效应的影响[12]。

但是mirror-EMD未充分考虑一点的就是噪声干扰问题，实际信号中，工况那么复杂，常常会夹杂着多种噪声干扰，而噪声会严重影响到mirror-EMD的分解质量。针对这个问题，先对信号做去噪处理，滤除多余干扰，凸显故障特征，接着对其应用镜像延拓法EMD分解，再对分解后的主IMF做相关系数法筛选，wt-mirror-EMD，这一方法也就应运而生。

4 相关系数法

在EMD分解过程中，常会因为其过分解导致虚假伪分量的产生，这些分量所含的能量值极小，往往是低频成分，假设把它们看成是有用分量去一起做频谱分析，其频谱线势必会产生干扰和杂波，对此问题，参照数学相似系数[13]概念，引入一种相关系数法来鉴别虚假分量，此方法通过计算各个IMF分量与原信号的相关系数，相关系数越大，则表示越相关。那么，哪些分量更相关，比较相关或者不相关呢？这就需要选定一个阈值，前人理论研究表明，阈值的选取通常为最大相关系数的1/10[14]即可，其具体计算公式如下：

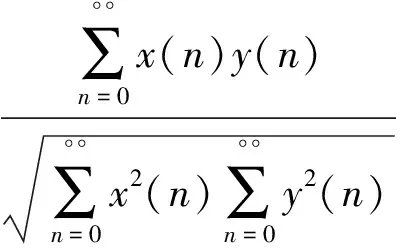
(2)

上式中，ρxy代表相关系数大小，x(n)、y(n)代表需要比较的两个序列。

5 仿真信号分析

本课题选用下面的信号仿真分析

a=cos(2*pi*10*t)+

10*cos(2*pi*50*t)+2*randn(1,1 000)

式中仿真信号由10 Hz和50 Hz两种频率成分组成，采样点数N为1 000，采样频率f为1 000 Hz，并加入了randn随机噪声，噪声强度为2，加噪后信号波形如图1所示，对该信号采用小波阈值去噪，阈值选取自适应阈值，经过反复多次试验，选定db3小波基并进行2层小波分解，去噪后信号波形如图2所示，分别对图1和图2信号进行EMD分解，然后选取主IMF分量作希尔伯特分析，得到波形如下，(a)图为用传统mirror-EMD方法得到的波形，(b)图为用改进wt-mirror-EMD方法得到的波形。

仿真结果分析：

观察图3(a)，传统改进mirror-EMD方法中，分解出了8个IMF分量和一个残余量，IMF1为其高频随机噪声干扰，理论上IMF2与IMF3分别应该对应仿真信号的两个谐波频率：10 Hz与50 Hz，但由于受到噪声的干扰，其分解的两个IMF幅值波形幅度不一，时大时小。将两分量重构，对重构后的信号作希尔伯特分析，由图4(a)、4(b)可看到其频谱图含有较多的虚假频率和杂波，尽管50 Hz的频率比较显著，但10 Hz的频率成分被噪声所淹没，无法区分清楚。

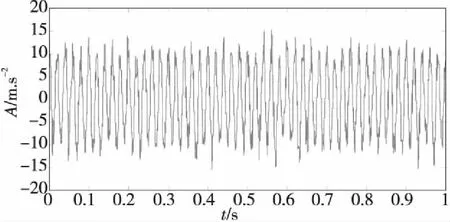
图1 仿真信号含噪波形

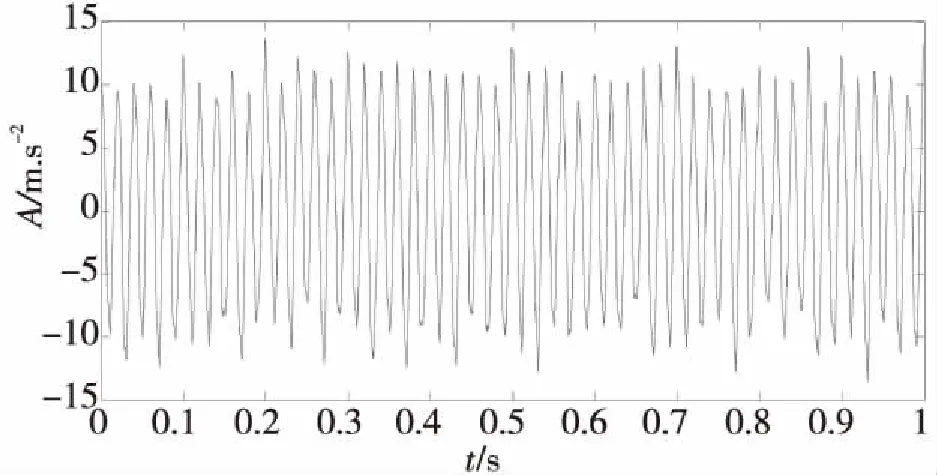
图2 去噪后波形

图3 EMD分解图比较Fig.3 The comparison of EMD decomposition chart

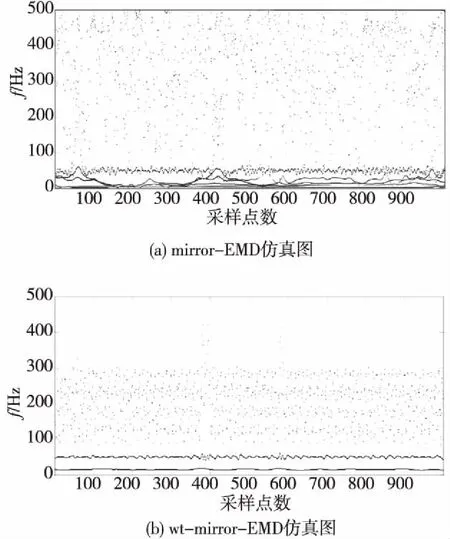
图4 希尔伯特谱图比较

观察图3(b)，采用本文wt-mirror-EMD方法分解，仅仅分解出5个IMF分量和一个残余量，不仅相对于图3(a)，虚假分量个数减少，而且本文方法去除了高频干扰成分，IMF1,IMF2分量波形较平稳，其后对此两个主IMF分量重构，对重构后信号作希尔伯特分析，由4(b)、5(b)两图可明显清晰看出50 Hz，10 Hz的频率成分，这是由于自适应小波阈值去噪在一定程度上滤除了噪声影响，更加凸显了故障信息，可见本文方法相对传统方法的有效性。

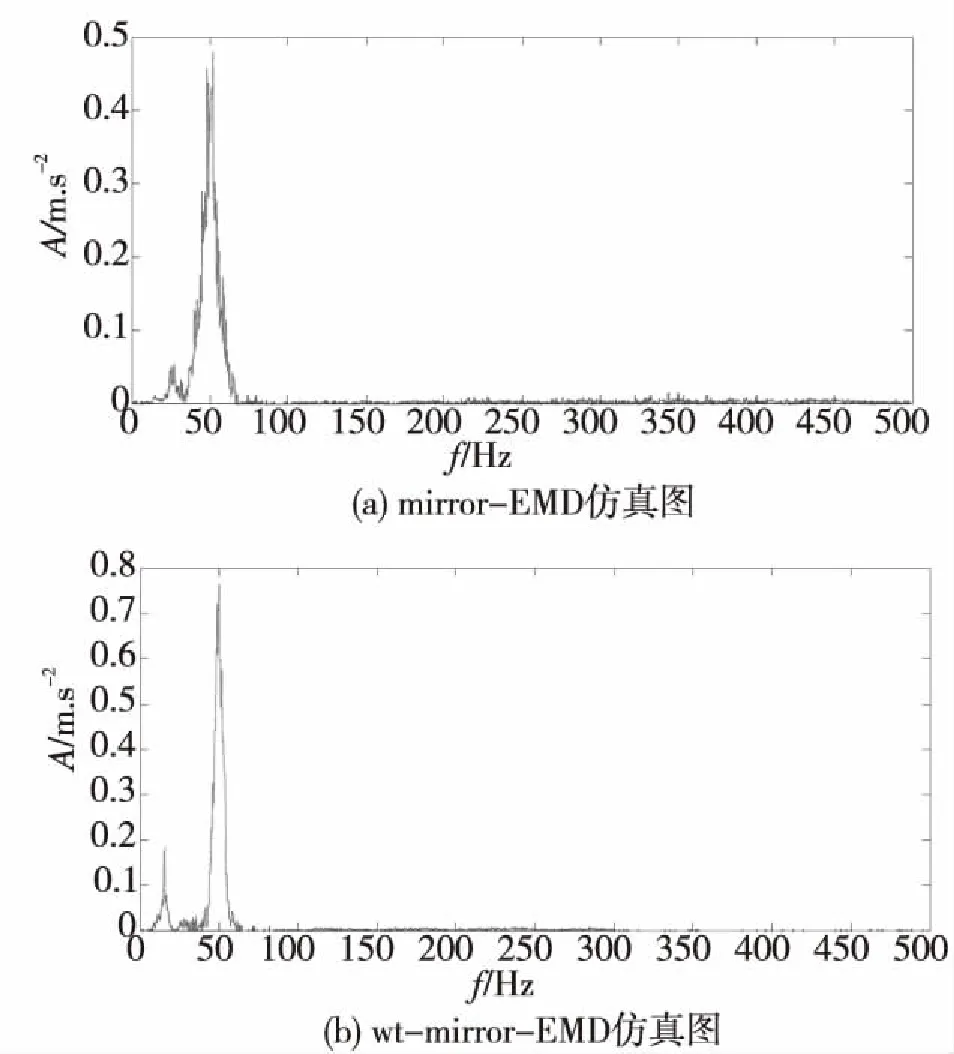
图5 希尔伯特边际谱图比较

6 实际轴承信号的分解

本实验所用轴承数据来自西储大学电气工程实验室，选用6205-2RSJEM SKF深沟球轴承，该实验设置内圈故障直径0.014 inch，在轴承座安装加速度传感器，用来采集信号，采样频率为12 000 Hz，采样点数为1 024个，轴承旋转频率29.95 Hz，发动机转速1 797 r/min.按照理论计算，可得到其内圈故障特征频率为162.21 Hz.原信号时域波形如图6所示，对该故障波形去噪，阈值选取自适应阈值，经过反复多次试验，采用db3小波并进行2层分解，重构后的去噪信号如图7所示

比较图6与图7，去噪后的信号明显降低了噪声干扰，故障冲击成分更加明显，接着对去噪后的波形进行经验模态分解，得到了7个固有模态IMF分量和一个残余量,如下图8所示。

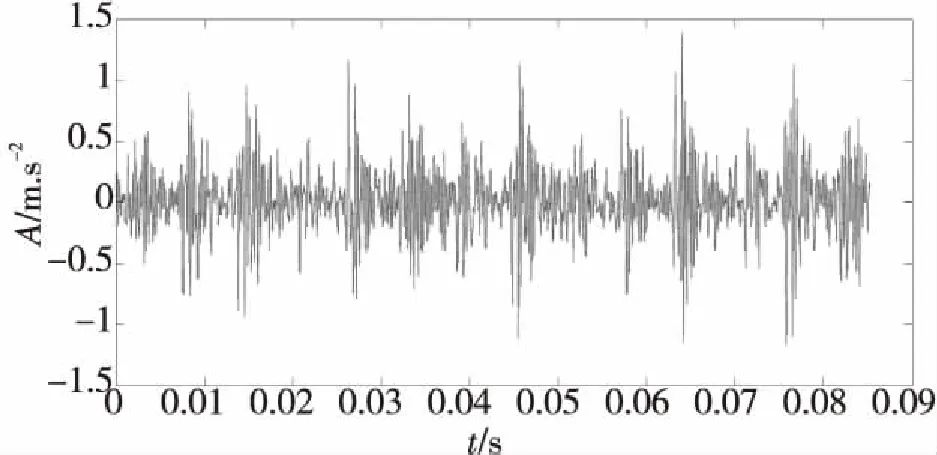
图6 原故障信号波形

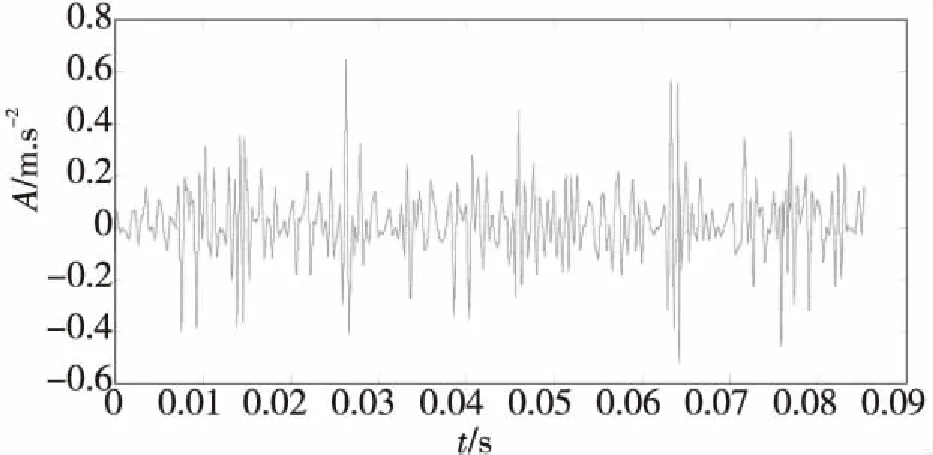
图7 去噪后波形

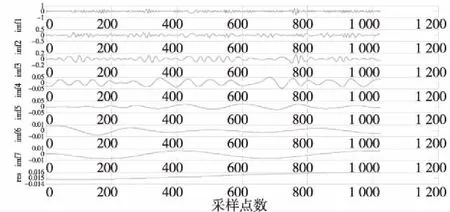
图8 wt-mirror-EMD分解图

在根据上述公式计算出各IMF分量与去噪后信号的相关系数，7个IMF分量相关系数分别为0.656 2、0.426 3、0.213 2、0.077 0、0.009 5、0.003 8、0.004 0，根据阈值的设置通常为序列中最大相关系数的1/10原则，可得阈值为0.065 62，由此可知前4个IMF分量包含了轴承故障的主要特征，其余IMF则为虚假分量，将前4个IMF重构，对重构后的主IMF做包络谱分析，包络谱波形如图9(b)所示，同理，对原信号进行传统改进EMD方法分解，筛选出主IMF并做包络谱分析，包络谱波形如图9(a)所示。

实际轴承仿真分析：

图9(a)mirror-EMD中，前3个较高频率冲击成分分别为60 Hz、104.38 Hz，161.9 Hz，其中60 Hz接近旋转频率的二倍频，161.9 Hz虽接近轴承内圈理论故障特征频率162.21 Hz，但是在其104.38 Hz处存在较高的虚假频率冲击成分，易对分析故障类型产生误判，而在图9(b)wt-mirror-EMD方法中，可以清晰地看出只有两个较高的频率冲击成分，60 Hz与161.9 Hz，60 Hz对应着二倍旋转倍频，161.9 Hz频率接近轴承内圈故障频率162.21 Hz，中间的虚假成分幅值减弱，而且300 Hz后的干扰成分也得到了一定程度抑制。

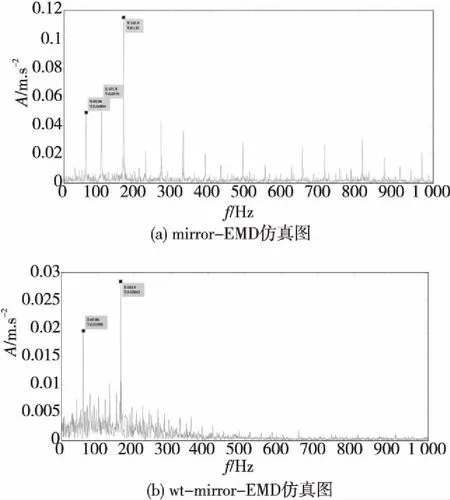
图9 IMF包络谱图比较

7 结 论

本文采用先对故障信号小波去噪处理，在对去噪后信号EMD分解wt-mirror-EMD方法，滤除了原故障信号中的大部分干扰和噪声分量，噪声对分解结果的影响也就微乎其微，得到的IMF分量更加准确，通过仿真和实测轴承信号验证了此方法的可靠性。

[1] 李兴林，张仰平，曹茂来,等. 滚动轴承故障监测诊断技术应用进展[J]. 工程与试验，2009，49(4):1-5.

[2] 李舜酩，郭海东，李殿荣. 振动信号处理方法综述[J]. 仪器仪表学报，2013，34(8):1907-1915.

[3] FLANDRIN P，RILLING G，Goncalves P. Empirical mode decomposition as a filter bank[J]. IEEE Signal Processing Letters，2004，11(2):112-114.

[4] 董银峰，李英民，赖明. 基于EMD和VARMA模型的结构损伤识别[J]. 振动与冲击，2010，29(12):141-147.

[5] 杨晓萍，刘普森，钟彦儒. 基于经验模式分解的有源滤波器谐波检测[J]. 电工技术学报，2009，24(5):197-202.

[6] 刘立君，王奇，杨克己,等. 基于EMD和频谱校正的故障诊断方法[J]. 仪器仪表学报，2011，32(6):1278-1283.

[7] 祁艳杰，王黎明，杨泽辉,等. 几种改善EMD端点效应方法的比较研究[J]. 现代电子技术，2013,36(22):50-52.

[8] 黎恒，李智，莫玮,等. 噪声干扰环境下抑制EMD模态混叠方法[J]. 信号处理，2015,31(8):956-961.

[9] 张德丰. MATLAB小波分析[M]. 北京：机械工业出版社，2009.

[10] 郭继坤，马鹏飞，赵肖东. 基于新阈值函数的小波阈值去噪算法及仿真[J]. 工业仪表与自动化装置，2015(1):117-121.

[11] 杨永锋. 经验模态分解在振动分析中的应用[M]. 北京：国防工业出版社，2013.

[12] 曹端超，康建设，赵劲松,等. EMD端点效应抑制方法仿真比较与实例分析研究[J]. 机械传动，2013,37(3):83-87.

[13] 晋民杰，王快，范英,等. 一种基于相似系数的权重确定方法[J]. 太原科技大学学报，2015,36(1):60-64.

[14] 丁常富，蔡志成. EMD中有效IMF选取方法的研究[J]. 热力发电，2014,43(1):36-40.

ApplicationofImprovedEMDinFaultDiagnosisofBearing

SUN Yong-peng, DONG Zeng-shou

(School of Electronic Information Engineering, Taiyuan University of Science and Technology,Taiyuan 030024, China)

In signal decomposition process, traditional mirror extension of empirical mode decomposition is susceptible to random noise and is also easily to produce false IMF components. To solve these shortcomings, a new EMD method is proposed, it combined adaptive wavelet threshold denoising, mirror extension EMD and the removal of false component with correlation coefficient. For this method, the first step is to denoise the original fault signal, and then the denoising signal with mirror extension of empirical mode decomposition is decomposed. In this way, some IMF components can be got. Finally, the correlation coefficient of IMF was calculated, the spectrum of high correlation coefficients of IMF components was analysed. Both the simulation and the actual bearing signal analysis show that the proposed method is more accurate than the traditional EMD, especially when there is noise interference.

wavelet threshold denoising, mirror extension EMD, bearing,fault diagnosis

1673-2057(2018)01-0025-06

2016-07-26

太原科技大学校博士启动基金(20132021)

孙永鹏(1989-)，男，硕士研究生，主要研究方向为电气设备故障诊断。

TH133.33

A

10.3969/j.issn.1673-2057.2018.01.005