α稳态分布噪声下单基MIMO雷达DOA估计
2018-01-09楼顺天郭艺夺
宫 健,楼顺天,郭艺夺
(1.西安电子科技大学,陕西西安710071;2.空军工程大学,陕西西安710051)
α稳态分布噪声下单基MIMO雷达DOA估计
宫 健1,2,楼顺天1,郭艺夺2
(1.西安电子科技大学,陕西西安710071;2.空军工程大学,陕西西安710051)
MIMO雷达实际中的噪声通常是没有二阶以上的矩的α稳态分布冲击噪声,基于二阶或更高阶累积量的常用角度估计算法很难实现目标DOA估计。为此,提出了一种基于FLOM-RC-MUSIC算法的MIMO雷达DOA方法,通过利用匹配滤波后数据先进行降维处理,减小了算法的运算复杂度,再构造分数低阶协方差矩阵实现对冲击噪声的有效抑制,弥补了传统的处理算法不适用于冲击噪声的缺陷,增强了噪声子空间估计算法的稳健性。
α稳态分布;MIMO雷达;噪声子空间;目标定位
0 引言
相较传统相控阵雷达,MIMO雷达在杂波抑制、目标检测及参数估计等方面[1-5]均具有明显优点,同时还具有抗干扰能力强和截获概率低的特性[6-7],因此关于MIMO雷达的研究已成当前新体制雷达技术研究的热点,并取得了一系列的理论成果和实验结论。但是,以上研究大多都是基于Gauss噪声环境假设的,尤其是有关冲击噪声背景下的MIMO雷达角度估计的文章还鲜见报道。大量的试验数据表明,雷达实际的工作环境经常是在冲击噪声背景下,这种噪声具有代数拖尾概率密度函数,服从α稳态分布且不具有二阶以上的矩,这就意味着高斯噪声背景下基于二阶或更高阶累积量的角度估计算法的性能将急剧下降。鉴于此,解决冲击噪声背景下MIMO雷达的目标角度估计问题具有重要的理论意义和应用价值。
1 MIMO雷达噪声模型和信号模型
1.1 冲击噪声模型及其特点
大量研究表明冲击噪声服从α稳态分布,通过对其特征函数求反傅里叶变换可以得到α稳态分布的概率密度函数,满足下式:
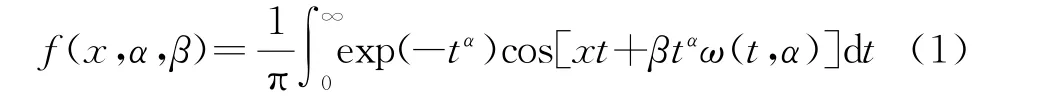
式中:α为特征指数,α∈(0,2],代表了分布冲击性的大小;β为对称参数,β∈[-1,1],代表了分布的扭曲程度,当β=0时的分布称为对称α稳态分布(SαS)。
用Matlab仿真不同α时SαS的随机变量样本如图1所示,该图可以反映冲击噪声的脉冲特性。
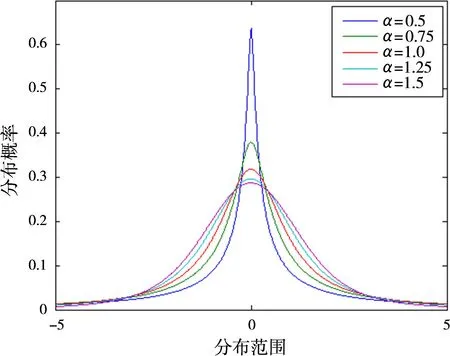
图1 SαS分布噪声脉冲特性
由仿真可以看出,α值越小,分布的拖尾越长,相应的分布的冲击性越强;相反,随着α值增大,分布的拖尾变薄,分布的冲击性变弱。结合式(1)可知,当α=2时,式(1)变成了Φ(t)=exp{jμtγ|t|α},为高斯分布;当α=1,β=0时为柯西分布,这一点通过仿真图可以得到印证。通常,为了区分α=2的高斯分布和0<α<2的非高斯稳态分布,定义后者为分数低价α稳态分布。
1.2 MIMO雷达的信号模型
考虑如图2所示的MIMO雷达系统,其中阵列天线收发共用,并且为M阵元的等距离线阵,阵元间距分别为d,为保证各接收信号不产生分辨模糊,取d=λ/2,λ为载波波长。
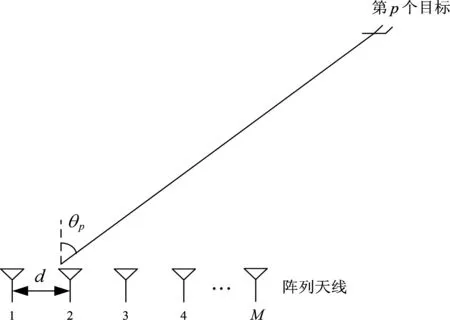
图2 MIMO雷达的阵列天线结构
MIMO雷达各发射阵元同时发射相互正交的信号。假设雷达远场有P个目标,DOA为θp。则目标为理想点目标情况下,接收的回波信号为
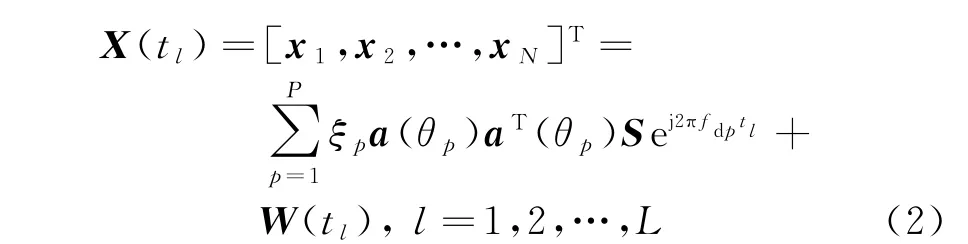
式中:x n为第n个接收阵元接收的回波信号;ξp为第p个目标的反射系数;fdp为第p个目标的多普勒频率;a(θp)为阵列对应于第p个目标的导向矢量,表达式为
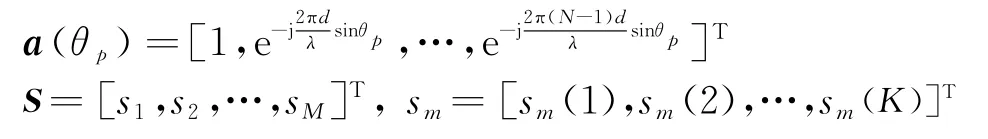
表示第m个阵元发射的正交信号;W(t l)∈C N×K为冲击噪声,K为每个脉冲重复周期内的快拍数,L表示脉冲数。
接收端匹配滤波器的结构如图3所示,则接收的回波信号经过匹配滤波后,可得
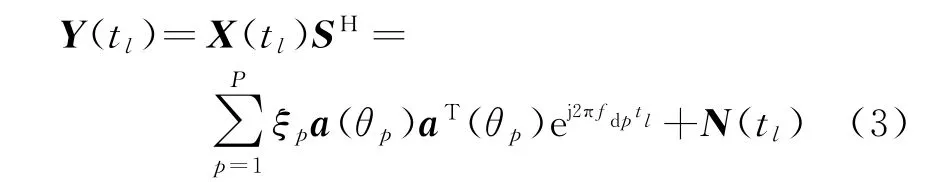
式中,N(t l)=W(t l)SH为滤波后噪声矩阵。
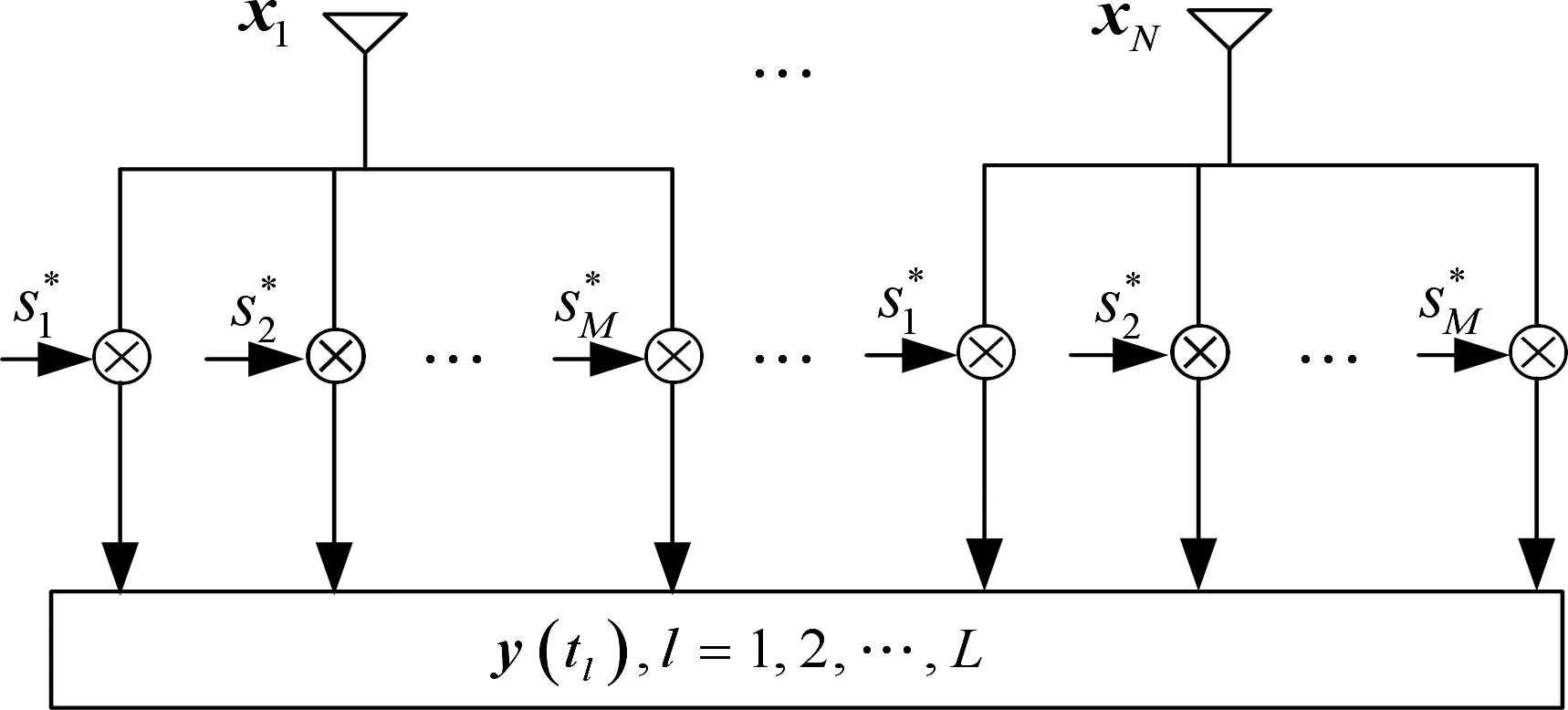
图3 MIMO雷达匹配滤波处理
将Y(t l)按列堆栈并表示成矩阵形式,可得
式中,A=[a(θ1)⊗a(φ1),a(θ2)⊗a(φ2),…,a(θP)⊗a(φP)],a(t l)=ξpej2πfdptl,n(t l)=vec(N(t l)),vec(·)表示将矩阵按列向量化,⊗表示Kronecker积。
2 基于噪声子空间的目标角度估计方法
2.1 MIMO雷达低复杂度MUSIC算法
构造MUSIC空间谱函数为
式 中,a(θp)=[1,ex p(-j sin(θp)),… ,exp(-j(M-1)sin(θp))]H。
对函数fMUSIC(θp)进行搜索,则最大峰值处即可作为目标的角度估计值。但是这种基本的M USIC算法的计算复杂度较高。本文采用一种基于降维变换处理的低复杂度M USIC算法(RC-MUSIC)。
构造矩阵G,使下式成立:
则矩阵A可以表示为
式中,B=[b(θ1),b(θ2),…,b(θK)]∈C(2M-1)K。
根据式(7),定义W=GHG,可以将W写成

假设数据的噪声子空间为E n,因此可以构造RC-M USIC空间谱函数为
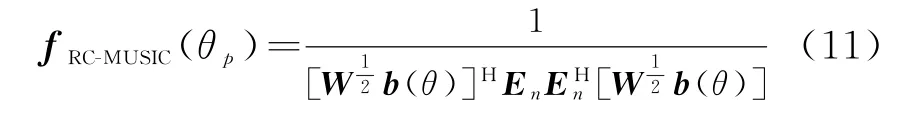
函数fRC-MUSIC(θp)的P个最大峰值处即为目标的角度估计值。
2.2 FLOM-RC-MUSIC算法原理
当噪声背景为冲击噪声时,接收数据y′(t l)不具有二阶以上的矩,这就意味着上述RC-MUSIC算法中噪声无法获得协方差矩阵,为此可以重构随机变量y′(t l)的分数低阶协方差FLOM[8]为
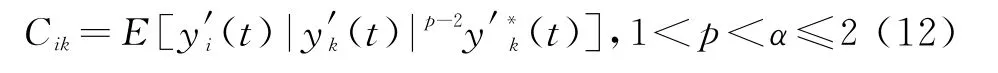
式中 ,y i(t),y k(t)为MIMO雷达的输出。从C ik的公式可以看出,重构的分数低阶协方差是共轭对称的,并且当1<α≤2时是有界的。
将其代入算法并写成矩阵的形式为
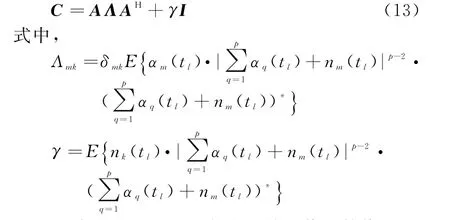
矩阵C的M2-P个较小的特征值的数值为γ,这些特征值对应的特征矢量张成与矩阵A的各个列向量正交的噪声子空间E n。
根据以上的推导,将FLOM-RC-MUSIC算法的步骤总结如下:
Step 1:对MIMO雷达匹配滤波后的数据进行降维变换为
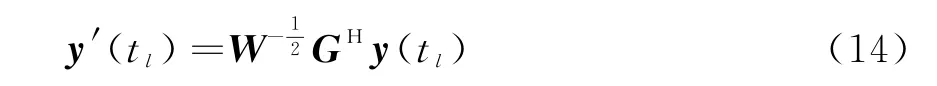
Step 2:计算M2×M2维分数低阶协方差矩阵,其元素为
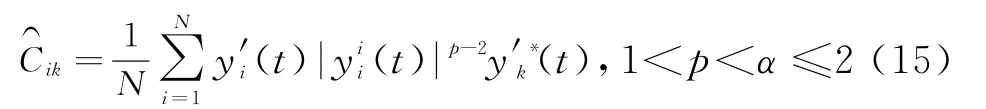
Step 4:通过对式(11)函数fRC-MUSIC(θp)进行搜索,估计P个目标的角度值。
3 算法性能仿真分析
冲击噪声的分布特性可以根据特征指数α和分散系数γ来决定,因而可以用信号平均功率和分散系数γ的比值即广义信噪比(GSNR)来代替一般信噪比,表达式如下:
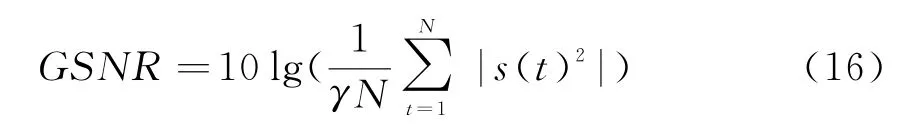
式中,N为采样快拍数。当α=2时,广义信噪比与普通的信噪比一样。
实验1:假设空中存在两个目标,目标相对阵列天线的角度分别为20°和45°,取α=1.5的SαS分布的独立冲击噪声,采用阵元数为8的均匀线阵,快拍数为1 024,GSNR=10 d B,分别使用传统的M USIC算法和FLOM-RC-M USIC算法进行角度估计,得到算法的谱峰搜索图如图4所示。
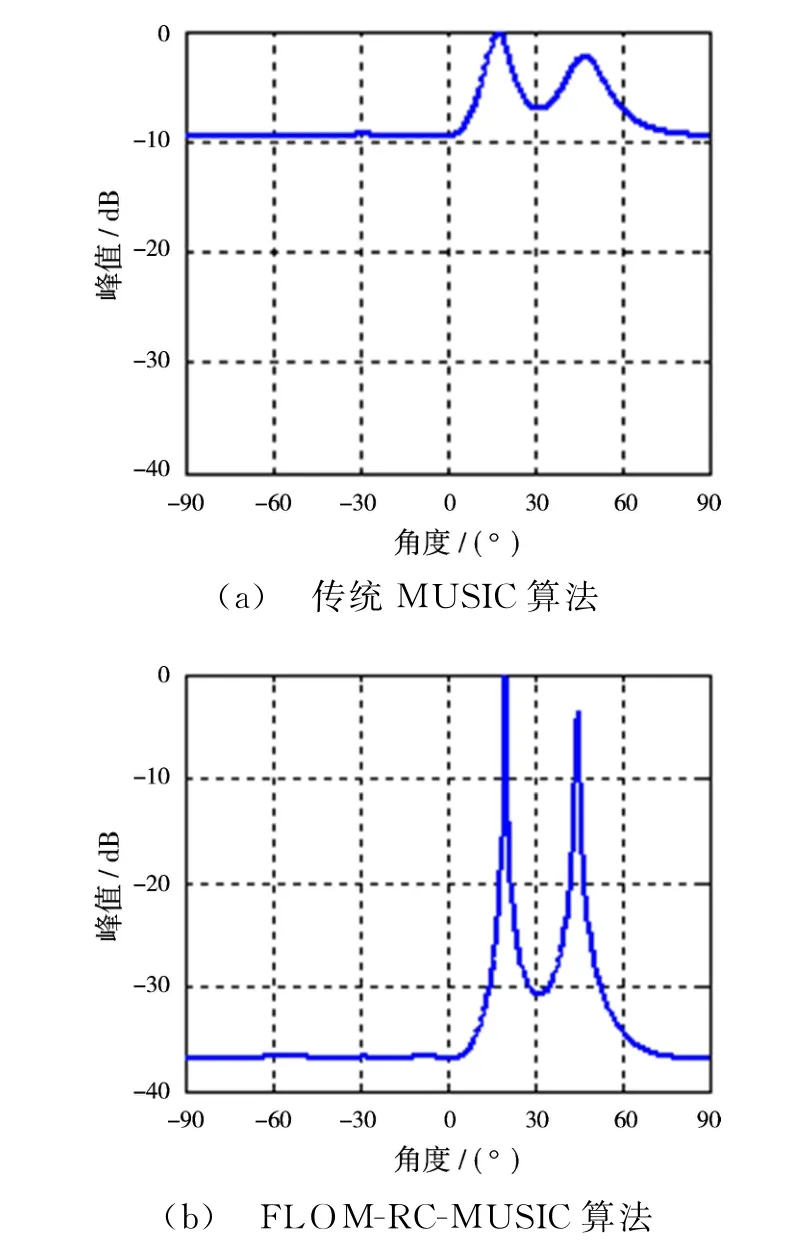
图4 两种算法角度估计的谱峰搜索图
由仿真结果可以看出,传统的MUSIC算法对强冲击噪声的抑制作用较差,伪峰和干扰较大,而且谱峰不够尖锐;而本文采用的FLOM-RC-M USIC算法对冲击噪声具有较好的抑制作用,而且谱峰明显,角度估计性能要明显优于传统的算法。
实验2:定义目标角估计的均方根误差(RSME)为
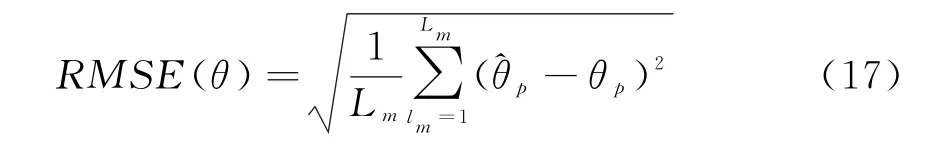
式中,L m为Monte Carlo实验的次数,分别为目标的角度估计值和实际值。
假设空中目标相对阵列的角度为10°,采用阵元数为8的均匀线阵,快拍数为1 024,分别使用传统的MUSIC算法和FLOM-RC-MUSIC算法对目标进行50次Monte Carlo实验,得到目标的角估计均方根误差(RMSE)随广义信噪比(GSNR)的变化,如图5所示。
由仿真可知,本文所采用的FLOM-RC-MUSIC算法在冲击噪声背景下具有比传统的MUSIC算法更好的估计性能;随着信噪比增大,RMSE逐渐减小,即角度估计性能随着信噪比的增大逐渐提高。
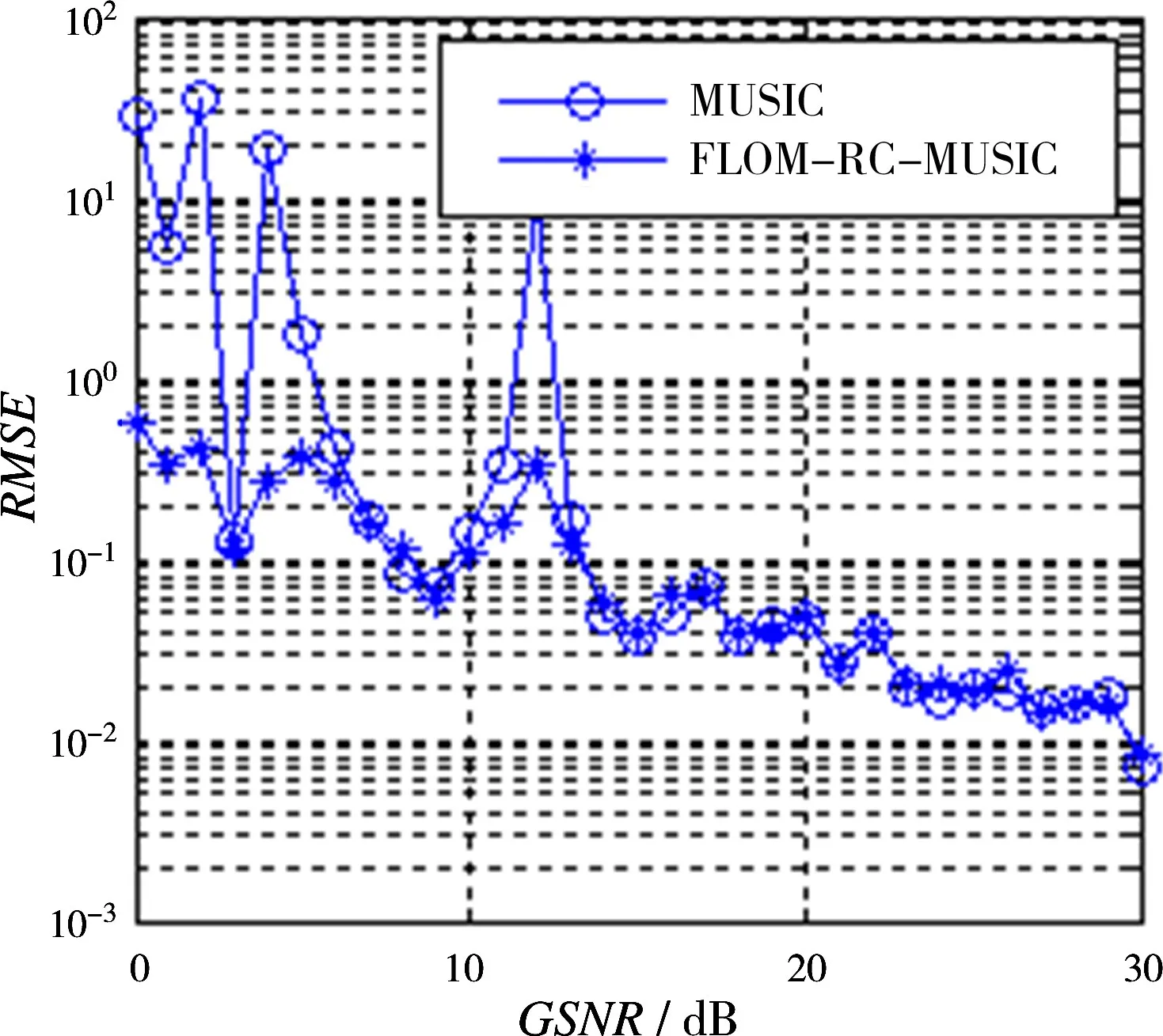
图5 两种算法RMSE随GSNR变化关系
4 结束语
本文提出了一种基于FLOM-RC-MUSIC算法的MIMO雷达收发角度估计方法,算法通过预先对MIMO雷达匹配滤波后数据进行降维变换,有效减小了角度估计的运算复杂度,再利用构造的分数低阶协方差矩阵实现了对服从SαS稳态分布冲击噪声的有效抑制,弥补了传统的二阶或四阶统计模型及相应的处理算法不适用于冲击噪声环境的缺陷,增强了噪声子空间估计算法的稳健性,研究新的方法对MIMO雷达的实用化和工程化能够起到一定的推动作用。
[1]HU Tong,ZHANG Gong,LI Jianfeng,et al.Angle Estimation in MIMO Radar with Non-Circular Signals Based on Real-Valued ESPRIT[J].Acta Aeronautica et Astronautica Sinica,2013,34(8):1953-1959.
[2]BENCHEIKH M L,WANG Y D,HE H Y.Polynomial Root Finding Technique for Joint DOA DOD Estimation in Bistatic MIMO Radar[J].Signal Processing,2010,90(9):2723-2730.
[3]徐定杰,李沫璇,王咸鹏,等.色噪声环境下双基地MIMO雷达收发角度估计[J].哈尔滨工程大学学报,2013,34(5):623-627.
[4]BENCHEIKH M L,WANG Y.Joint DOD-DOA Estimation Using Combined ESPRIT-MUSIC Approach in MIMO Radar[J].Electronics Letters,2010,46(15):1081-1083.
[5]LIU F,SUN C,WANG J,et al.Virtual Unitary-ESPRIT Algorithm for Joint DOD and DOA Estimation in Bistatic MIMO Radar[J].ICIC ExpressLetters,2010,4(5):1457-1463.
[6]马红星,陈思佳.水面杂波背景的统计MIMO雷达检测方法研究[J].雷达科学与技术,2015,13(5):479-484.MA Hongxing,CHEN Sijia.Statistical MIMO Radar Detection Approaches Against Water Clutter[J].Radar Science and Technology,2015,13(5):479-484.(in Chinese)
[7]刁鸣,安春莲.冲击噪声背景下的DOA估计新方法[J].北京邮电大学学报,2013,36(5):99-104.
[8]刁鸣,刘磊,安春莲.冲击噪声背景下独立信号与相干信号并存的测向自适应新方法[J].中南大学学报(自然科学版),2016,47(1):108-113.
DOA Estimation in Monostatic MIMO Radar Under Alpha Stable Distribution Noise
GONG Jian1,2,LOU Shuntian1,GUO Yiduo2
(1.Xidian University,Xi’an710071,China;2.Air Force Engineering University,Xi’an710051,China)
The MIMO radar is usually with algebraic tail probability density function of the impulsive noise.This noise has no more than two orders.It is difficult to accurately locate the target when the algorithm is based on the two or higher orders.A new DOA estimation method based on FLOM-RC-MUSIC algorithm is presented.By using the matched filter data and then dimensionality reduction,the computational complexity of the algorithm is reduced.The effective suppression of noise impact is achieved.The algorithm enhances the robustness of the noise subspace algorithm.
alpha stable distribution;MIMO radar;noise subspace;target location
TN958;TN974
A
1672-2337(2017)01-0039-04
10.3969/j.issn.1672-2337.2017.01.007
2016-08-23;
2016-09-28
国家自然科学基金(No.61601502,61501501);航空基金(No.20150196007,20150196003)

宫健男,1984年7月出生于山东德州,博士研究生,主要研究方向为MIMO雷达信号处理。E-mail:xidianbo2014@163.com
