一种旋翼叶片微动特征提取新方法

2018-01-09

雷达科学与技术 2017年1期

(空军预警学院三系,湖北武汉430019)

一种旋翼叶片微动特征提取新方法

陈永彬,李少东,杨军,陈梁栋

(空军预警学院三系,湖北武汉430019)

利用旋翼目标的旋转运动引起的微多普勒效应,实现目标微动特征的准确提取,可为目标的精确识别提供重要依据。该文以旋翼叶片为例,提出一种基于自相关函数和图像域的微动特征快速提取方法。首先基于目标的回波信号的周期性,利用回波自相关函数的图像峰值位置与目标旋转频率的关系,实现旋转频率的快速提取。然后在图像域提取目标微多普勒特征的边缘信息,通过边缘信息获得叶片散射点位置和初相信息。仿真结果验证了该方法的有效性。

相关性;图像域;旋翼叶片;特征提取

0 引言

通过对自旋等微动目标,如直升机旋翼、弹头进行特征参数提取,获得其结构、尺寸等物理特征,可为目标探测、识别提供重要的依据,因此应用微动特征识别目标成为近年来空间探测、反导防御等领域的研究热点[1-3]。

自Chen提出微多普勒的概念以来,有关微动特征提取的技术,如时频分析方法、回波分析方法、参数估计与提取方法等受到众多研究人员的关注。文献[4]提出一种基于短时迭代自适应(Short Time Iterative Adaptive Approach,STIAA)的时频分析方法,在一定程度上获得了较高的时频分辨率和较小的交叉项影响。文献[5]利用统计学的直方图获得了良好的刚体点和旋转点的回波分离,具有比文献[6]中基于L-statistics的回波分离方法更好的效果。文献[7]利用时频分布的循环相关系数进行了目标自旋速度的估计方法研究。文献[8]利用一维高分辨径向距离测量方法对微动特征参数进行提取。文献[9]基于宽带雷达利用回波的高阶矩函数提取目标的旋转频率、半径和初相等微动特征。

为进一步提升目标微动特征的提取能力,本文在旋翼叶片散射点的微多普勒效应分析的基础上,提出了一种基于自相关函数和图像域的微动特征提取方法。该方法利用回波信号的周期性与自相关函数峰值位置的关系,快速准确提取旋翼叶片的旋转频率。通过图像处理方法对微多普勒特征进行预处理,在此基础上利用边缘信息获得叶片散射点位置和初相信息。仿真结果表明该方法能快速、有效地提取目标微动特征,并具有一定的抗噪性。

1 旋翼叶片散射点微多普勒效应分析

从电磁散射的观点来看,旋翼的每个叶片由散射中心组成,而每个散射中点都被考虑成具有某种反射率的点[10]。由文献[11]可知在处理带有方向的桨叶时,总是将其等效为多个散射点,为了便于分析,本文将叶毂(旋转中心)认为是强散射点,即旋翼每个叶片等效为4个散射点。雷达与旋翼散射点的空间几何关系如图1(a)所示,其二维关系(投影至平面XOY)如图1(b)所示。

图1 雷达与旋翼散射点的几何关系

设雷达视线与旋翼中心O′的初始距离为R0,方位角和俯仰角分别为α和β(图1(b)为α=β=0°的情况),旋翼叶片以恒定的旋转频率frot绕旋翼中心旋转(Ω=2πfrot),叶片长度为l。叶片上的散射点P i到旋翼中心的距离为x i(0≤x≤l),初始旋转角为θ1。通常悬停情况下有R0≫x i,则P i与雷达的距离[10]为

当雷达发射载频为fc的单频连续波信号,散射点P i的基带回波为

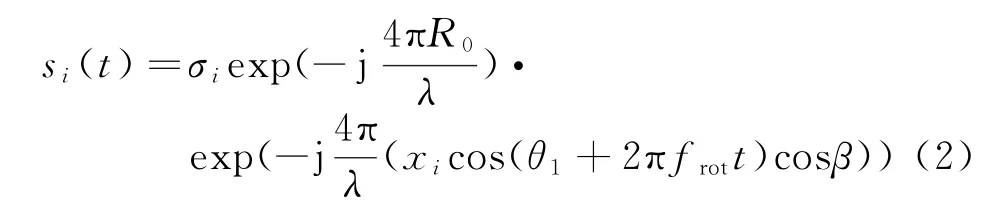
式中,σi为后向散射系数。

假设旋翼共有N个叶片(每个叶片上有K个散射点),则N个叶片有N个不同的初始旋转角,即

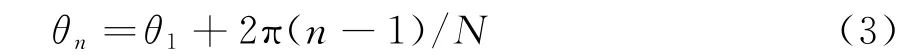
令每个叶片的散射点有一样的散射系数和位置,则旋翼回波可表示为

由式(4)可知由第n个叶片上第i个散射点引起的相位函数为

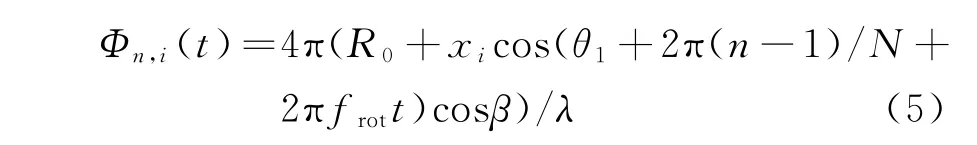
由此可得该点引起的多普勒频率为

由式(6)可知,散射点的微多普勒呈现正弦函数形式,而正弦函数的周期与旋翼旋转周期是一致的,即

式中,Trot=1/frot为旋翼的旋转周期。

且由式(6)可知,不同叶片上散射点引起的微多普勒曲线有着不同的初相,而同一叶片散射点初相是一致的,差异在于多普勒频率峰值的差异。结合式(6)可综合判断叶片数目和初相、散射点个数和位置等微动特征。

2 微动特征的提取

2.1 旋转频率的提取

令t=t+Trot,代入式(4),有

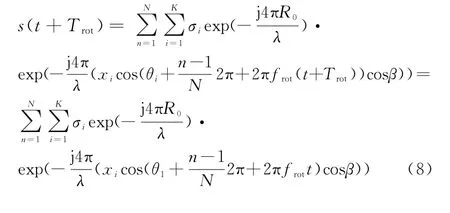
即

由式(9)可知,旋翼周期性的旋转微动导致雷达回波亦呈现周期性,因此可利用回波相关性[12]进行估计旋翼周期,进而提取微动频率。

设旋翼叶片回波s(t)的离散表示为s(m),其中,m=1,2,…,M表示时域回波的第m个时间点,M为时域回波信号点数,则回波自相关可表示为

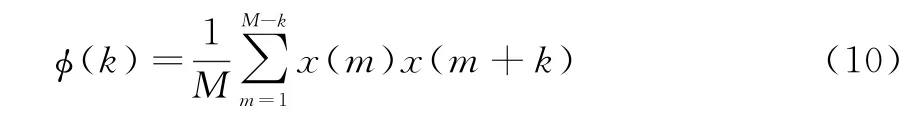
由函数相关特性可知,ϕ(k)在回波周期的整数倍处峰值,可反映回波的周期性。令相邻峰值之间的时间点平均间隔为,转换为时间间隔,即

此时估计目标的旋转频率f′rot为

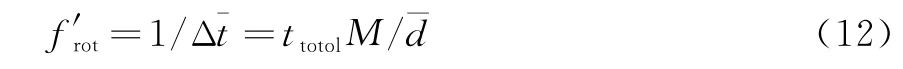
式中,ttotol为总观测时间。在处理过程中最终可直接将时间点m变为对应的时间刻度,这样可直接估计旋转频率。

由文献[13]对叶片的奇偶性与旋翼回波幅度闪烁[14]的关系分析可知,叶片的奇偶性将影响回波幅度的周期性。当叶片个数为偶数,即旋翼叶片处于对称状态时,对称的叶片引起的回波幅度将是相同的,而叶片个数为奇数时,由于叶片的非对称性,每个叶片引起的回波形式是一致的,只是位置有所差异,因此在时域上无法准确提取叶片的个数。而在微多普勒特征图像中可以明显地区分出每个叶片,故可结合时频分析先预判断叶片的个数,再更新由相关性提取旋转频率,即最终估计的旋转频率为

2.2 散射点位置、初相提取

以一个散射点为例,由式(6)有,假设cosβ=1,当微多普勒频率取到正最大值,即fd_n,i_max=4πfrotx i/λ,因此可提取表征散射点位置的特征x i,即

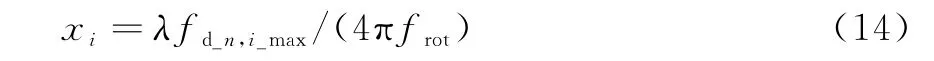
由于受到时频分布分辨率的制约,得到的微多普勒曲线往往存在一定的展宽效应,直接利用微多普勒曲线提取微动特征的准确性往往不高。而时频分布作为谱图,可考虑采用图像处理[15]的方式进行对谱图预处理,提高分析精度。数学形态学是图像信号处理的一个重要分支,为大量的图像处理问题提供了一种有力方法。如采用骨架提取算法提取旋翼微多普勒曲线的骨架,有利于消除展宽效应,提高时频分析的精度。

本文考虑将叶片散射点微多普勒曲线的谱图进行平滑处理,之后设置合适阈值将其转换为二值图像,在此基础上利用边缘检测技术提取曲线的边缘信息。检测出微多普勒曲线的边缘信息后,原先展宽的每一条“粗”微多普勒曲线将会变成两条“细”微多普勒曲线,但“细”曲线对应的旋转频率、微多普勒频率值和旋转初始角等参数都与“粗”曲线对应参数是一致的,只是在得到的基线位置上有所差异,通过对检测到的两条曲线的基线进行加权平均可得到准确的基线位置。利用对“细”微多普勒曲线进行参数估计将消除展宽效应,提高检测准确性。具体而言,假设两条“细”微多普勒曲线的峰值频率分别为d_n,i_max_1和d_n,i_max_2,利用加权平均思想可得该散射点的多普勒频率峰值为则结合2.1节估计的rot可提取散射点位置为

对于散射点初相而言,由于叶片之间是等分的,因此只需估计出一个叶片散射点的初相即可。利用上述均值方法可得某时刻t′的多普勒频率值,结合估计的rot和有初相为

综合2.1和2.2节的分析,基于相关性和图像处理的微动特征提取流程图如图2所示。

图2 基于相关性和图像域的微动特征提取流程

3 仿真与分析

本文使用仿真数据验证所提方法的有效性,仿真参数具体如下:雷达发射单载频脉冲,波长为0.15 m,脉冲重复频率为4 000 Hz,观测时间为1 s。雷达与旋翼中心的初始距离为50 km,与旋转平面的方位角和俯仰角均为0°。旋翼叶片数为2,叶片初相分别为0,πrad,旋转频率为2.667 Hz,每个叶片上散射点位置依次距离旋转中心为0,2.5,4和6 m,对应的散射系数依次为1,0.6,0.8和1。仿真的时域回波(加入10 dB的高斯白噪声)和微多普勒特征如图3所示。

图3 旋翼散射点仿真结果

3.1 提取旋转频率

由图3(a)的时域回波可知,回波呈现周期性,但从中无法直接提取周期,且无法准确提取旋翼叶片数目。而由图3(b)对称的微多普勒曲线可判断叶片数目=2。

对时域回波进行自相关处理,结果如图4所示。

图4 旋翼散射点回波的自相关

提取图4中归一化相关系数的相邻峰值时间依次为0,0.187 5,0.374 8,0.562 4,0.749 9,采用均值化处理可得,由式(13)解得2.666 7 Hz,与仿真值的误差小于1%。

3.2 提取散射点位置、初相

基于2.2节的图像处理分析,对时频分布图像(3(b))依次进行平滑处理、二值化处理、边缘检测和骨架提取,结果如图5所示。

由于在回波中加入10 dB的噪声,因此图3(b)除了显示散射点微多普勒频率曲线以外,背景还有噪声的影响,采用维纳滤波进行平滑处理,得到图5(a)的结果,此时微多普勒特征图像中的背景噪声已经被较好地消除了。再进一步将图5(a)转换为二值图像(如图5(b)所示),图中黑色代表1,白色背景代表0。基于此,利用边缘检测算法提取到的边缘信息如图5(c)所示,再对此进行骨架提取可得图5(d)的结果,此时时频分析的精度比图3(b)有所提高。虽然图5(c)、(d)并不能很好地解决部分图像交叉的问题,但并不影响我们进行散射点位置和初相的提取。

图5 微多普勒特征图像处理结果

首先分析图5(c),提取图中第一个最大频率值的信息为(0.092 73 s,1 409 Hz),利用此信息提取图中该列含有的微多普勒正频率值(含零频附近的值)依次为1 409 Hz和1 278 Hz,957.4 Hz和827.1 Hz,616.5 Hz和506.5 Hz,85.21 Hz和-75.19 Hz,即根据2.2节分析利用均值可得4个频率值依次为1 343.5,892.25,561.5和5.01 Hz。同理分析图5(d),图中第一个最大频率值信息为(0.092 73 s,1 348 Hz),提取该列的微多普勒正频率值依次为1 348,897.2,566.4和5.013 Hz。

利用式(15)和相对误差可得图5(c)、(d)提取散射点位置的结果,如表1所示。

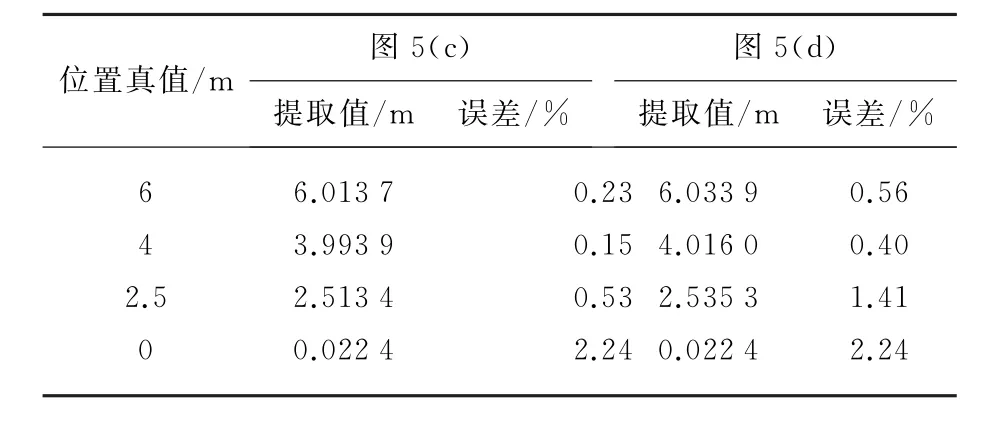
表1 提取散射点位置结果对比

由表1可知,图5(c)、(d)提取的散射点位置信息的误差均在一定可承受的范围内,验证了基于图像处理的提取方法的合理性。同时对比两者误差可知,利用边缘检测再进行均值的方法有助于提高特征提取的精度。

利用图5(c)提取的频率值信息(0.092 73 s,1 343.5 Hz)和对应的位置信息^x=6.013 7 m,由式(16)可得该点的初相为-0.017 1 rad,与仿真值误差为1.71%。由两个叶片的对称性可知另一叶片散射点初相为3.124 5 rad。

3.3 不同信噪比下提取微动特征的均方根误差分析

为验证在不同信噪比(SNR)下本文方法提取微动特征的鲁棒性,本文进行蒙特卡罗实验,并进行均方根误差(Root Mean Square Error,RMSE)分析。

首先分析旋转频率,则RMSE的表达式为

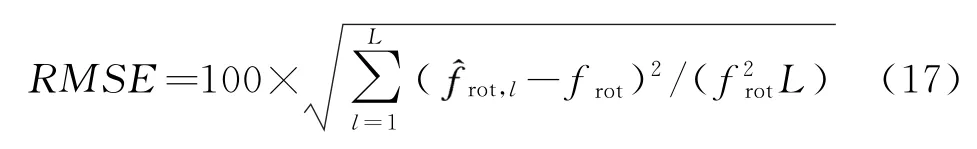
式中,L为蒙特卡罗实验次数,本文取L=100,为每一估计的旋转频率。本文设置SNR的范围为-20～14 dB,步进2 d B,图6为RMSE结果。

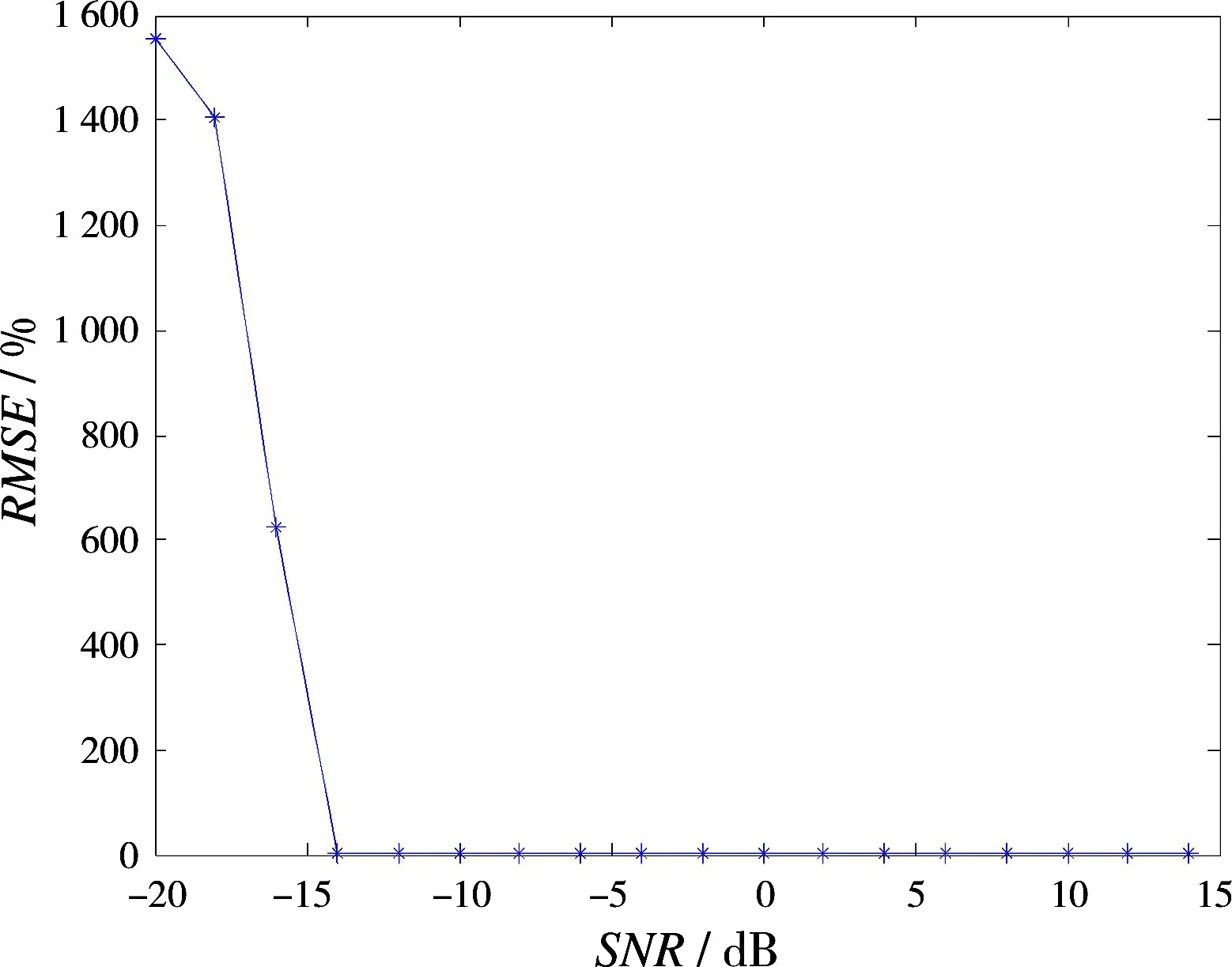
图6 提取旋转频率的RMSE结果

由图6可知,估计旋转频率的RMSE随着信噪比(SNR)的提高而降低,当SNR达到-14 dB以上时,RMSE的值小于1%,说明基于自相关的频率估计方法具有一定的抗噪性。

其次分析散射点位置和叶片初相:由于散射点位置和叶片初相都不是单一的,此时求出每一个散射点位置或叶片初相的RMSE,然后取均值作为散射点位置或叶片初相的均方根误差值。由于在低信噪比的条件下,时频分析结果中散射点的微多普勒曲线往往被噪声淹没,因此本文主要考虑时频分析结果较好的情形,即SNR的范围为-2～14 dB,设置步进2 d B,RMSE结果如图7所示。

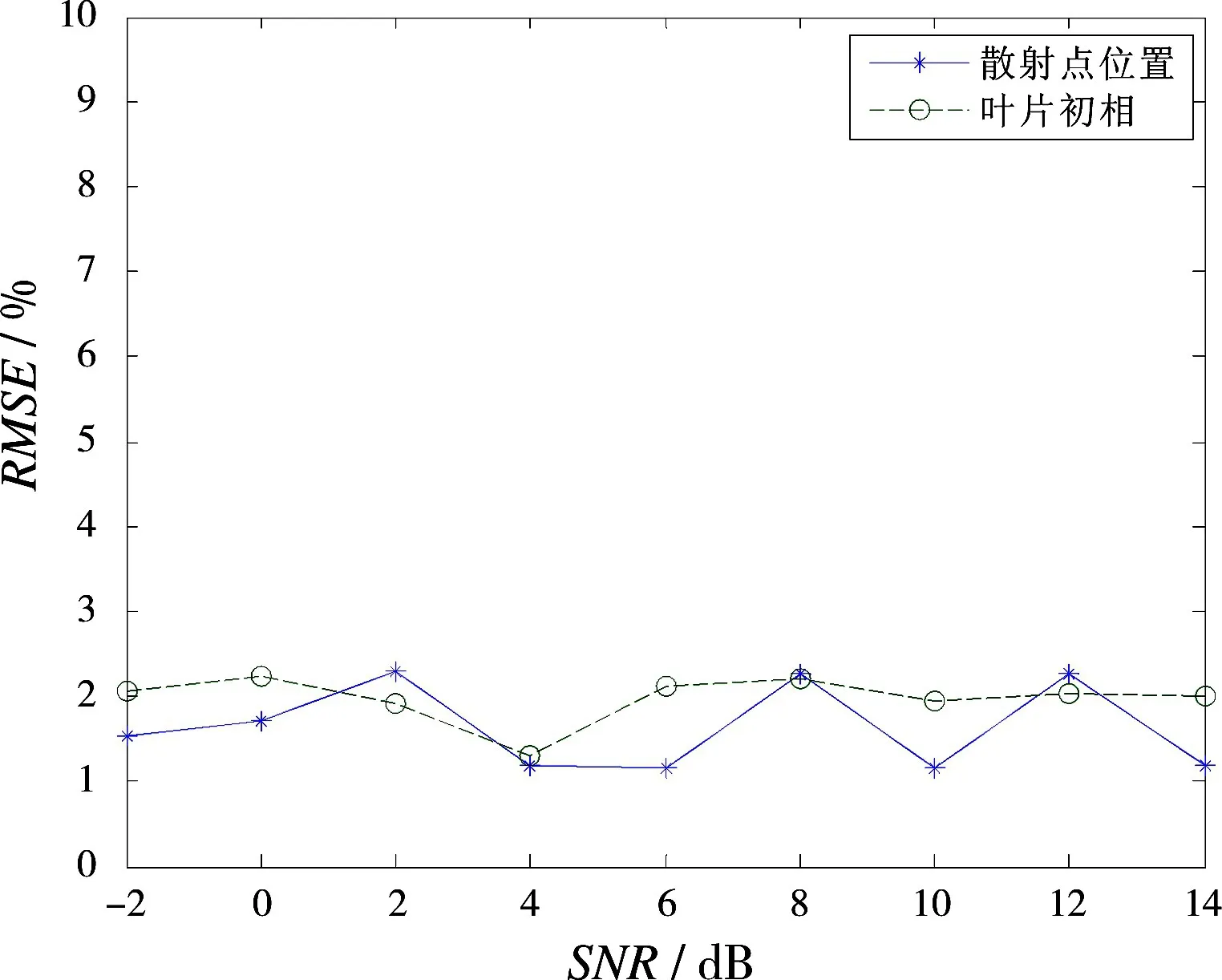
图7 提取散射点位置和叶片初相的RMSE结果

由图7可知,提取散射点位置和叶片初相的RMSE随着信噪比(SNR)的提高呈波动状态,但RMSE的值均处于小于3%的状态,验证了在信噪比为-2～14 dB情况下,利用图像域提取的散射点位置和初相的方法的有效性。

4 结束语

雷达目标微动特征的提取已成为当前目标分类和识别领域研究的一个热点。本文提出了一种基于自相关和图像域的微动特征提取方法。该方法利用回波信号的周期性,通过寻找回波自相关函数的峰值位置,快速准确地获得了旋翼叶片的旋转频率。通过图像处理方法对微多普勒特征进行预处理,在此基础上利用边缘信息准确地获得了叶片散射点位置和初相信息。仿真结果表明该方法能快速、有效地提取目标微动特征,并具有一定的抗噪性。

[1]宋新景.低分辨雷达的目标分类识别研究[J].雷达科学与技术,2016,14(3):286-290.SONG Xinjing.Target Identification for Low Resolution Radar[J].Radar Science and Technology,2016,14(3):286-290.(in Chinese)

[2]BAI Xueru,ZHOU Feng,BAO Zheng.High-Resolution 3-D Imaging of Group Rotating Targets[J].IEEE Trans on Aerospace and Electronic Systems,2014,50(2):1066-1077.

[3]胡晓伟,童宁宁,何兴宇,等.基于窄带雷达组网的高速自旋目标成像[J].系统工程与电子技术,2016,38(4):792-798.

[4]赵彤璐,廖桂生,杨志伟.基于短时迭代自适应—逆Radon变换的微多普勒提取方法[J].电子学报,2016,44(3):505-513.

[5]ZHANG Rui,LI Gang,ZHANG Y D.Micro-Doppler Interference Removal via Histogram Analysis in Time-Frequency Domain[J].IEEE Trans on Aerospace and Electronic Systems,2016,52(2):755-768.

[6]STANKOVIC L,THAYAPARAN T,DAKOVIC M,et al.Micro-Doppler Removal in the Radar Imaging Analysis[J].IEEE Trans on Aerospace and Electronic Systems,2013,49(2):1234-1250.

[7]ZHANG Wenpeng,LI Kangle,JIANG Weidong.Parameter Estimation of Radar Targets with Macro-Motion and Micro-Motion Based on Circular Correlation Coefficients[J].IEEE Signal Processing Letters,2015,22(5):633-637.

[8]HONG Ling,DAI Fengzhou,LIU Hongwei.Motion-Parameter Estimation for Precession-With-Nutation Space Targets Based on Wideband Radar Measurements[J].IEEE Trans on Aerospace and Electronic Systems,2016,52(2):643-657.

[9]邓冬虎,张群,李宏伟,等.基于高阶矩函数的宽带雷达微动特征提取[J].电子与信息学报,2013,35(9):2126-2132.

[10]CHEN V C.The Micro-Doppler Effect in Radar[M].Norwood,MA:Artech House,2011.

[11]HUO Kai,LIU Yongxiang,HU Jiemin,et al.A Novel Imaging Method for Fast Rotating Targets Based on the Segmental Pseudo Keystone Transform[J].IEEE Trans on Geoscience and Remote Sensing,2011,49(4):1464-1472.

[12]高铭江.弹道目标运动参数估计方法研究及软件设计[D].西安:西安电子科技大学,2014.

[13]杜兰,李林森,李玮璐,等.基于时域回波相关性特征的飞机目标分类方法[J].雷达学报,2015,4(6):621-629.

[14]陈永彬,李少东,杨军,等.旋翼叶片回波建模与闪烁现象机理分析[J].物理学报,2016,65(13):1-11

[15]张群,罗迎.雷达目标微多普勒效应[M].北京:国防工业出版社,2013.

A New Method for Micro-Motion Signature Extraction of Rotor Blades

CHEN Yongbin,LI Shaodong,YANG Jun,CHEN Liangdong

(No.3Department,Air Force Early Warning Academy,Wuhan430019,China)

The micro-Doppler(m-D)effect induced by the rotating motion of the rotor target can be used to extract the micro-motion signature exactly,which can provide an important basis for the accurate indentification of the target.Taking rotor blades as an example,a fast extraction method based on the autocorrelation function and the image domain is proposed in this paper.Firstly,based on the periodicity of the target’s echo,it can realize the fast extraction of the rotation frequency by finding the correlation between the peak position of the echo autocorrelation function and the rotation frequency.Then,the edge information of the m-D signature is extracted in image domain.The position and initial phase of the scattering points are obtained by using the edge information.Computer simulation verifies the effectiveness of the proposed method.

correlation;image domain;rotor blades;signature extraction

TN957.52

1672-2337(2017)01-0013-06

10.3969/j.issn.1672-2337.2017.01.003

2016-07-12;

2016-08-28