中国实验快堆堆坑在丧失外电源事故下的温度分布数值模拟

马崇扬，张东辉，王长茂，别业旺

(1.中国原子能科学研究院，北京 102413；2.环境保护部核与辐射安全中心，北京 100082)

中国实验快堆堆坑在丧失外电源事故下的温度分布数值模拟

马崇扬1，张东辉1，王长茂1，别业旺2

(1.中国原子能科学研究院，北京 102413；2.环境保护部核与辐射安全中心，北京 100082)

堆坑是中国实验快堆(CEFR)的重要组成部分，它采用通风冷却的方法来降低堆坑混凝土温度，防止其温度过高、脱水而导致支撑堆容器的力学性能降低。本文对丧失外电源事故下的堆坑内部温度分布进行了二维数值模拟，采用Jones-Launder的k-ε低Reynolds数湍流模型。得到了堆坑温度场、保温层外壁和混凝土内壁在竖直方向的温度分布、混凝土内壁最高位置温度随时间的变化，为CEFR运行提供参考。

中国实验快堆；堆坑；温度分布；数值模拟

中国实验快堆(CEFR)堆坑(见图1)由整体的钢筋混凝土浇筑，为圆柱状空间。堆坑作为CEFR主要的安全包容设施之一，其内安装的设备有保护容器、主容器及堆本体构件，堆坑上部由堆顶固定屏蔽密封。其中，保护容器外壁包有保温层，用来减少一回路系统热量的损失。正常运行工况时，CEFR堆坑冷却由反应堆装置冷却通风系统进行强迫冷却，但在该系统丧失动力电源后，堆芯余热及反应堆蓄热经主容器、保护容器及其保温层最终传至堆坑，堆坑混凝土温度过高将引起混凝土脱水，进而可能破坏混凝土的力学性能，使其失去对堆容器的支撑作用，引起严重安全事故。因此，必须分析研究在失去通风冷却功能后，保温层外壁温度、混凝土内壁温度和堆坑温度场的变化以及这些变化对堆坑混凝土的影响程度。在冷却通风系统丧失动力电源丧失情况下，自然对流是最主要的换热方式，因此，需对这种情况下堆坑内部产生的自然对流进行研究。

本文的研究初始假设是：额定功率运行时，全厂失去外电源导致紧急停堆工况下，操纵员在半小时内未进行干预，堆坑失去强迫循环冷却。本研究基于原始变量有限容积法，SIMPLE算法处理压力与速度耦合，湍流模型采用Jones-Launder[1]的k-ε低Reynolds数模型，对堆坑的温度分布进行数值研究，数值结果可为CEFR运行提供参考。

1 基本模型与数学描述

1.1 问题描述与模型

在动力电源丧失情况下，我们只关心堆坑内的温度场、混凝土内壁和保温层外壁的温度分布。要对图1所示的环形空间进行数值模拟非常困难，因此对它进行保守的简化处理。

(1) 忽略CEFR堆坑内构件的影响，认为堆坑为轴对称竖直封闭环形腔，采用二维模型；

(2) 计算热边界为保护容器，取CEFR额定功率运行时保护容器壁实测温度，并认为短时间内不变化；

(3) 考虑混凝土厚度和保护容器外壁保温层厚度，但不计算固体区域的温度分布，采用附加源项法处理混凝土和保温层边界；

(4) 忽略堆顶固定屏蔽和堆坑底部的散热；

(5) 不考虑辐射换热的影响；

(6) 牛顿流体，忽略黏性耗散。

图1 CEFR堆坑示意图Fig.1 Schematic diagram of CEFR reactor pit

计算边界条件：

(1)混凝土外壁温度303.15K；

(2)保护容器壁温度533.15K；

(3)堆坑上部和下部绝热；

(4)固体壁面的速度、湍流动能及其耗散率为零。

物性参数选取：保温层材料导热系数取0.0705W/(m·K)，混凝土导热系数取0.79W/(m·K)，空气导热系数取0.029W/(m·K)。计算流体为空气(Pr=0.69)，符合Boussinesq假设，计算时间步长为0.0372s。

1.2 控制方程

通用控制方程(圆柱坐标：x为垂直方向坐标，r为半径方向坐标)：

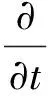
(1)

式中：

质量方程：Γ=1，φ=1，S=0

(2)

动量方程：

对于速度分量u：Γ=η+ηt，φ=u，

(3)

对于速度分量v：Γ=η+ηt，φ=v，

(4)

(5)

S=Gk+Pb-ρε+Dk

(6)

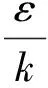
(7)

其中：

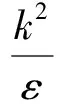
(8)

(9)

(10)

(11)

(12)

(13)

(14)

(15)

c3=tanh|u/v|

(16)

β=1/Tref，Tref=(TC+TH)/2

(17)

cμ=0.09，cε1=1.44，cε2=1.92，σk=1.0，σT=0.9，σε=1.3。

利用附加源项法处理边界(保温层和混凝土厚度)，具体推导过程参考文献[2-3]，这里只列出结果，如下所示。

高温侧：

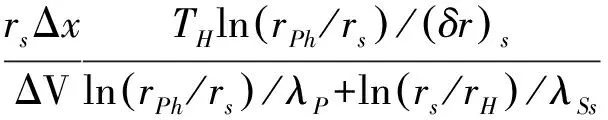
(18)

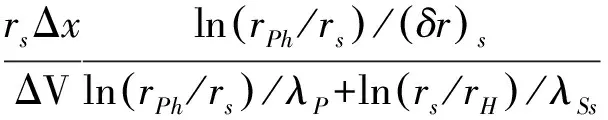
(19)

低温侧：

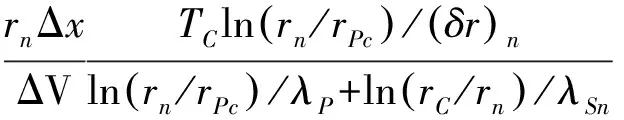
(20)

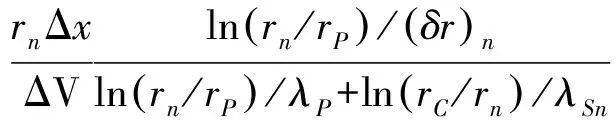
(21)

保温层外壁局部Nu定义为：

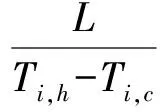
(22)

保温层外壁平均Nu数为：

(23)

式中：φ——通用变量；

Γ，S——广义扩散系数和源项；

x，r——空间坐标，m；

u，v——x和r方向速度分量，m·s-1；

p——压力，Pa；

T——温度，K；

g——重力加速度，m·s-2；

ρ——流体密度，kg·m-3；

k——湍流动能，m2·s-2；

ε——湍流动能耗散率，W·kg-1；

ηt——湍流动力黏性系数，Pa·s-1；

η——分子动力黏性系数，Pa·s-1；

t——时间变量，s;

β——热膨胀系数，K-1；

λSs——保温层导热系数，W·(m·K)-1；

λSn——混凝土导热系数，W.(m·K)-1；

λP——流体的导热系数，W·(m·K)-1；

rs，——保温层外壁半径，m；

rn——混凝土内壁半径，m；

rPh——与保温层最近节点的半径，m；

rPc——与混凝土最近节点的半径，m；

rH——保护容器外壁半径，m；

rC——混凝土外壁半径，m；

(δr)s——保温层与最近的节点的距离，m；

(δr)n——混凝土与最近的节点的距离，m；

Δx——边界控制容积的宽度，m；

ΔV——边界控制容积的体积，m3；

TC——混凝土外壁温度，K；

TH——保护容器壁温度，K；

Ti，h——热边界第i节点的温度，K；

Ti，c——冷边界第i节点的温度，K；

A——热边界的表面积，m2；

Ai——热边界第i个控制容积换热面积，m2；

L——特征尺度(取堆坑空腔的宽度)，m。

计算区域的初始条件：

u=v=k=ε=0，T=303.15K。

本文采用基于原始变量的有限容积法，将所计算的区域划分成一系列控制容积，每个控制容积都有一个节点作代表，通过将控制方程对控制容积做积分来导出离散方程，其中对流-扩散项离散采用乘方格式。用迭代法求解该离散方程，求解过程中用SIMPLE方法处理压力与速度耦合。判断计算收敛的标准是|(Nu(k+n)-Nu(k))/Nu(k+n)|≤10-6，其中n=10。采用非均分网格，使用文献[4]中的加密方法对壁面进行加密处理，取102×82，162×102非均分网格进行验算，所得Nu相对差别小于0.5%，可将102×82非均分网格计算结果可看成与网格无关的解，因此本计算中采用非均分网格102×82。

2 计算结果与分析

2.1 堆坑温度场分布

图2 堆坑等温线图 (K)Fig.2 Isotherms of reactor pit (K)

图2示出了在稳态时堆坑腔内的等温线图，由图可知，堆坑内温度场在垂直方向出现分层现象，且温度逐步升高，这是由于高温壁面与低温壁面温差较大，使得自然对流换热强度大。

2.2 混凝土内壁和保温层外壁温度分布

图3示出了在稳态时保温层外壁和混凝土内壁在竖直方向的温度分布，由图可知温度分布都随竖直方向高度的增加而增加，保温层外壁的最高和最低温度分别为480K和389.9K，混凝土内壁的最高和最低温度分别为437.7K和347.7K。

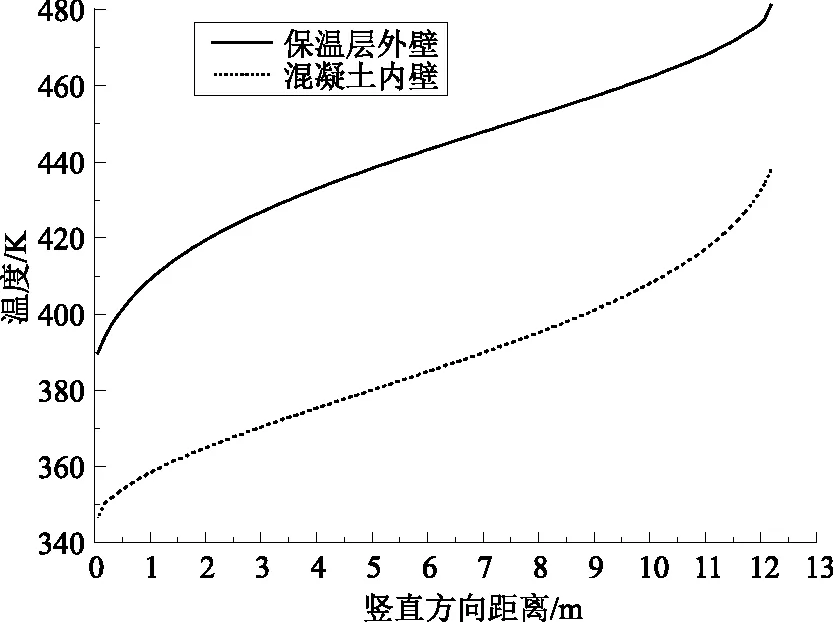
图3 保温层外壁和混凝土内壁在竖直方向的温度分布Fig.3 The temperature distribution of the outer insulation wall and inner concrete wall in the vertical direction

2.3 混凝土内壁最高位置温度随时间的变化

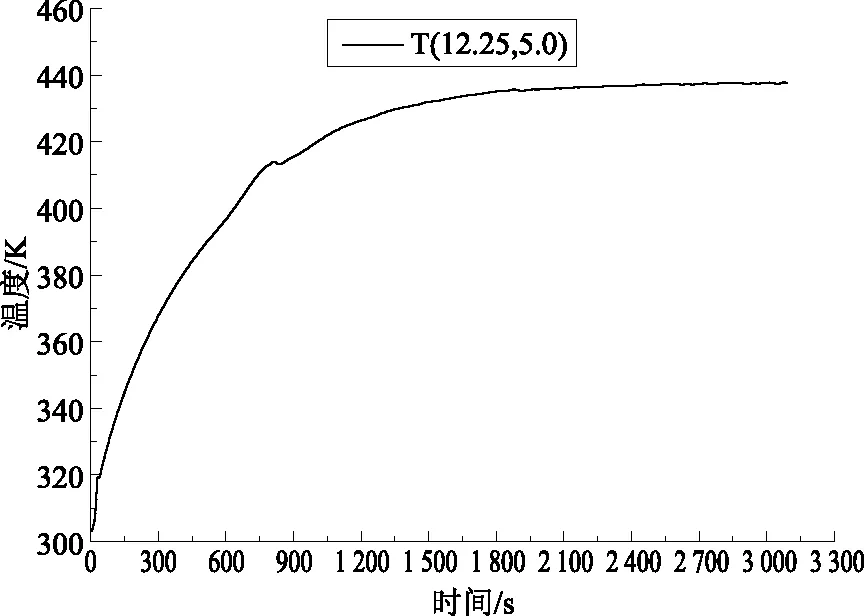
图4 混凝土内壁最高位置温度随时间的变化Fig.4 The change of inner concrete wall temperature in the highest spot with the time

图4示出了T(12.25，5.0)温度随时间的变化，其中T(12.25，5.0)表示竖直方向距离12.25m，径向距离5.0m位置的温度，为混凝土内壁最高位置的温度，由图4可知，刚开始温度迅速上升，在200s时，温度达到353K，在2400s以后，温度基本维持在437.7K。从图4可以发现在815s到832s之间，温度由414K下降至413.2K，温度下降0.8℃，之后温度又开始上升，可能是由于流动的不稳定引起的温度波动。

本文计算冷边界为恒温303.15K，热边界恒温533.15K，当堆坑内的流动和传热不随时间变化时可认为达到稳态阶段。

3 结论

本文使用Jones-Launder的k-ε低Reynolds数湍流模型对CEFR堆坑在丧失外电源冷却下的温度分布进行了数值模拟，计算结果显示。

(1) 堆坑内温度场在垂直方向出现分层现象，且温度逐步升高。

(2) 保温层外壁的最高和最低温度分别为480K和389.9K，混凝土内壁的最高和最低温度分别为437.7K和347.7K。

(3) 混凝土内壁最高位置的温度在200s时，温度达到353K；在2400s以后，温度基本维持在437.7K。

上述计算结果可为CEFR运行提供参考。

[1] Henkes R A W M，Vlugt F F V D，Hoogendoorn C J. Natural convection flow in a square cavity calculated with low-Reynolds-number turbulence models[J]. International Journal of Heat & Mass Transfer，1991，34(91)：377-388.

[2] 陶文铨.数值传热学[M]. 2版. 西安：西安交通大学出版社，2008.

[3] 杨世铭，陶文铨.传热学[M]. 三版. 北京：高等教育出版社，2003.

[4] 马洪林. 封闭腔内高瑞利数(Ra)层流与湍流自然对流数值模拟[D]. 华中科技大学，2004.

NumericalSimulationofCEFRReactorPitTemperatureDistributionintheAccidentofPowerSupplyFailure

MAChong-yang1，ZHANGDong-hui1，WANGChang-mao1，BIEYe-wang2

(1. Institute of Atomic Energy，Beijing 102413，China;2. Nuclear and Radiation Safety Center，MEP，Beijing 100082，China)

Reactor pit is the important component of CEFR. The pit concrete is cooled by the ventilation in order to avoid concrete high temperature and then dehydration. That leads to concrete strength deterioration and cannot support the reactor vessel. This paper studied the two-dimension numerical simulation of reactor pit temperature distribution in the accident of power supply failure. The Jones-Launder low-Reynolds-numberk-ε turbulent model is accepted. The temperature distribution of reactor pit，the temperature distribution of the outer insulation wall and inner concrete wall in the vertical direction and the change of inner concrete wall temperature in the highest spot with the time are obtained. These solutions are useful to the operation of CEFR.

CEFR；Reactor pit；Temperature distribution；Numerical simulation

2016-06-29

马崇扬(1983—)，男，陕西定边人，工程师，博士，现主要从事反应堆热工流体研究

别业旺，bieyewang@chinansc.cn

Tk124

A

0258-0918(2017)06-1008-05