干式储藏137Cs源反散射份额的计算研究
2018-01-08程昌浩颜拥军祁铁涛
程昌浩,颜拥军,祁铁涛,屠 荆
(1.南华大学核科学技术学院,湖南 衡阳 421001;2.西北核技术研究所,陕西 西安 710024)
干式储藏137Cs源反散射份额的计算研究
程昌浩1,颜拥军1,祁铁涛1,屠 荆2
(1.南华大学核科学技术学院,湖南 衡阳 421001;2.西北核技术研究所,陕西 西安 710024)
干式储藏137Cs源由于其自身结构特点,放射源发射的γ射线中含有反散射光子,采用此类型的储藏源校准剂量计,会存在一定的偏差。本文首先建立了多源照射器实验室三维模型,利用该模型理论计算并分析了实验室墙壁对反散射峰计数的影响。然后测量137Cs能谱,采用两种方式扣除康普顿坪并计算出反散射峰与全能峰的计数之比。实验解谱结果表明,在实验室内离源6m处反散射光子与661.66keV光子计数之比为0.0909,实验解谱数据与蒙卡模拟数据相对偏差为-13.8%。
137Cs源;反散射;干式储藏源;康普顿坪
活度很高的放射源储存方式一种是湿式存储(水池),通过水带走它的热量、屏蔽它的放射性。现在国际上比较成熟的,采用比较多的是另外一种,即干式储存。干式储存靠特殊气体、惰性气体或者空气对放射源进行冷却,也可以有效保障安全。干式储藏γ射线源常用来做剂量计校准,能量刻度等工作。但由于干式储藏源自身的结构特点,放射源不仅发射γ射线,还与源后屏蔽材料发生康普顿效应,产生反散射光子。虽然反散射光子能量低于全能峰光子,但是反散射光子注量与全能峰注量比例并不明确,采用此类型的储藏源校准剂量计,会存在一定的偏差。本文利用蒙卡程序和测量实验谱计算反散射峰与全能峰之比,以期对剂量校准工作提供更准确的数据。论文思路框架如图1所示。

图1 思路框图Fig.1 Train of thought
1 蒙特卡罗方法计算离源不同距离处反散射光子份额
某单位校准用γ射线多源照射器采用干法储源的方式,同时存储多枚防护级放射源[2],包括安全容器、准直装置、快门以及控制系统几部分。通过选择不同的放射源以及快门的开闭控制,来为核探测系统灵敏度标定、核仪器仪表检定等实验提供不同能量和强度范围的标准γ射线辐射场。各源之间的散射可以忽略不计[3],本实验采用137Cs源作为实验源。
干式储藏源结构不同于大型辐照源(见图2),其周围有很厚的屏蔽体,正前方有准直孔。正是由于这样的结构,γ射线与源衬材料发生康普顿效应,造成其测量能谱的畸变。研究表明,对于已知活度标准源发出某一能量的γ射线,都存在饱和厚度[4,5],即达到饱和厚度后,反散射光子计数不再发生变化,而干式储藏源的厚度远远大于饱和厚度,因此诸如此类储藏源的反散射光子计数都已达到最大。

图2 γ射线多源照射器结构模型1—放射源;2—安全容器;3—芯体;4—准直器;5—快门;6—光阑Fig.2 Gamma rays multi-source irradiator structure model
放射源实验室结构布局见图3所示。实验室空间大小为:长9.55m,宽4.12m,高4.2m,墙体材料为水泥,放射源主屏蔽体材料为铅,准直孔为钨合金,出射口加有5mm厚的石墨盲板。在准直孔水平高度正前方1m至6.8m分别设置直径为1cm的点探测器。

图3 实验室布局示意图Fig.3 Laboratory layout diagram
实验室墙壁会造成反散射光子计数的增加,因此在数值模拟中,分别对有实验室墙壁和无实验室墙壁情况下的反散射光子比例进行了计算。得出有墙和无墙情况下反散射比例的差别。
本文的模拟计算采用mcnp5程序对多源照射器及其实验室进行了建模,设置照射源为137Cs各向同性源,模拟计算得到的不同距离处的能谱见图4图与图5。从模拟计算结果可以得出,无论是否存在墙壁反射,137Cs干式储藏源在200keV附近都存在反射峰,但计数不同。

图4 有墙时离源不同距离137Cs能谱Fig.4 The 137Cs energy spectrum with wall at different distance to the source

图5 无墙时离源不同距离137Cs能谱Fig.5 The 137Cs energy spectrum without wall at different distance to the source
从模拟能谱可以看出,在有墙无墙的情况下,不同距离的反散射峰计数是不同的,无墙情况下的反散射峰为源本身所自有的,与墙壁散射无关。但实际情况是我们所有的实验都是在有墙的情况下进行的,无墙只是理想情况,因此,弄清反散射中墙壁的贡献份额同样十分重要。
在mcnp模拟中,将墙壁密度填充为0,代表是真空状态,墙壁主要成分为水泥,密度为2.3g/cm3,利用直径为1cm的点探测器进行计数,得到有墙情况下反散射与全能峰比例见表1,无墙情况下反散射与全能峰比例见表2。

表1 有墙时不同距离不同能区散射所占比例Table 1 The ratios of scattering in different range at different distance with wall

表2 无墙时不同距离不同能区散射所占比例Table 2 The ratios of scattering in different range at different distance without wall

表3 模拟计算反散射与661.66keV全能峰计数之比Table 3 Ratio of backscattering to 661.66 keV full-energy peak in simulation counting
从模拟计算结果可以得出:
1) 在有屏蔽墙时,随着测量点远离源中心位置,反散射在低能区(58~220keV)所占的比例呈下降趋势,与全能峰和总计数的比例呈上升趋势;
2) 在无屏蔽墙时,随着测量点远离源中心位置,反散射在低能区(58~220keV)所占的比例基本保持不变;
3) 对于源自身产生的散射能区与全能峰之比的接近10%,在小剂量的辐照实验及标定实验中,如果要达到较高的测量精度,则需要考虑这方面的影响。
2 实验测量谱解析反散射峰比例
本实验所用137Cs源出厂活度为10Ci,出厂时间为2007年,实验能谱测量时间为2014年11月20日至11月21日。由于放射源活度较高,近距离测量能谱会造成在PHA(脉冲高度分析)方式工作下的能谱分析系统死时间过高,计数率超过测量系统的上限。因此在测量时选取了小平面型HPGe探测器,该探测器具有对低能部分探测效率高,高能探测效率低的特点,具有良好的能量分辨率。本实验首先对探测器进行参数测试,测量了探测器离源不同距离的能谱;然后建立了HPGe探测器探头模型,并且利用建立的探测器模型对探测效率进行了计算;最后采用扣除数值模拟康普顿坪法和按比例扣除康普顿坪法,解析离源6m测量位置的反散射与全能峰计数之比。
2.1 探测器参数测试
要正确解析测量能谱的反散射峰,需要得到探测器的本征效率或者在不同距离的探测器效率。距离较远的探测效率标定比较困难,通过蒙卡模拟得到修正探测器模型,而后得到探测器的本征效率,这对于本实验是可行且值得探索的。为了使本征效率计算更为准确,首先利用标准源137Cs和152Eu获得探测器能量刻度和效率刻度,能量刻度曲线结果见图6,效率刻度曲线见图7。
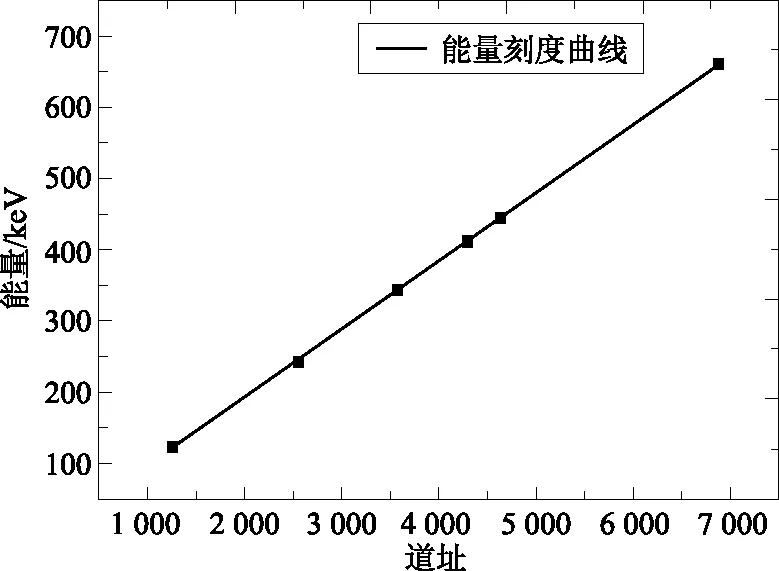
图6 HPGe探测器能量刻度曲线Fig.6 HPGe detector energy calibration curve

图7 HPGe探测器效率刻度曲线Fig.7 The HPGe detector efficiency calibration curve
从图6中可以看到,该探测器在我们所关注的能量范围120~670keV内具有良好的能量线性和能量分辨率,满足本实验的需求。
2.2 137Cs能谱测量
在对探测器进行了能量刻度后,继续添加液氮冷却探测器,待探测器性能稳定后对137Cs源进行测量。

图8 多源实验室本底谱Fig.8 The background energy spectrum of multi-source in the laboratory
从测量能谱来看,多源实验室本底谱相对于源能谱来说计数非常低,可以忽略。离源不同距离的137Cs实验测量能谱如图9所示。在137Cs测量能谱中,我们可以很明显地发现在200keV附近的反散射峰,这和我们在多源照射器数值模拟中看到的谱是一致的;其次就是在653keV附近出现小角散射峰,这也与数值模拟谱中观察到的现象是一致的。

图9 离源不同距离的137Cs能谱Fig.9 The 137Cs energy spectrum at different distance to the source
2.3 建立HPGe探测器数值模拟模型
在上面的实验及理论分析中我们发现建立HPGe探测器数值模拟模型是非常有必要的,而数值模拟一般是建立在实验基础上的,只有和实验数据吻合,才能说明建立的模型可用。因此我们首先在固定位置(相对较近的距离)用标准的137Cs、152Eu平面源对探测器进行效率刻度,然后结合ORTEC公司给出的产品说明书对建立的模型进行适当调节,从而得到准确可用的探测器模型。
HPGe探测器建模见图10所示,在建立探测器模型时忽略了对实验结果很小的液氮罐部分。

图10 HPGe探测器建模图Fig.10 HPGe detector modeling
通过计算模拟效率和实验效率之间的均方相对偏差来判断建立模型是否可用。均方相对偏差计算式为:
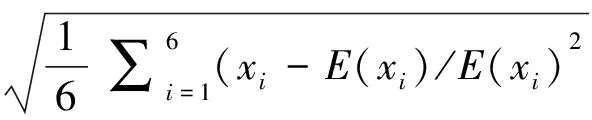
(1)
式中xi中为蒙卡计算效率,E(xi)为实验测量效率,i=1,2,3,4,5,6为分别表示为121.78keV,244.7keV,344.28keV,411.12keV,443.96keV,661keV 6种能量。最终得到HPGe理论计算效率与实验效率的对比见表4,效率相对偏差在7%之内,说明建立的模型可用[9]。

表4 实验效率与模拟计算效率相对偏差Table 4 The experiment and simulation computation efficiency relative deviation
2.4 反散射峰解析
如图3所示,在上面的模型建立好后,在探测器正前方设置单能单向平面源,平面源直径与探测器灵敏体积直径相同。得出单能康普顿坪实验能谱(见图11)。结合能谱图,确定反散射峰左边界点为170keV,右边界点为220keV。按照上述边界与本征效率可得出反散射峰面积,即:
(2)
式(2)中SR为反散射峰面积,Si为扣除康普顿坪后每道计数,εi为对应能量的本征效率。表5列出了170~220keV和661.66keV的本征效率,其他能量本征效率可以通过插值得出。
由第一部分模拟计算结果可知,测量点距离源中心位置6m以上时墙壁散射增加,然而对放射源自身的反散射却变化不大。考虑实际情况后选取6m这一个测量位置的能谱进行解析对比,将测量能谱中的反散射峰扣除康普顿本底后,利用修正的探测器模型计算出本征效率后,便可以得出实验测量中的反散射光子与661.66keV光子计数之比,由表6数据得到两者之比为0.1261。而经过理论计算得出两者之比为0.1055。

图11 单能康普顿坪实验能谱Fig.11 The spectrum of monoenergetic Compton plateau

表5 本征效率计算结果Table 5 The intrinsic efficiency of the detector

表6 峰面积计算结果Table 6 The results of calculation of peak area
从上面的能谱实验结果及分析可以看出,正确解析反散射峰面积关系到整个实验结果的准确性。除了扣除数值模拟康普顿坪法之外,我们也可以通过理论推导实验能谱中反散射注量与全能峰注量之比,然后按比例扣除康普顿坪。
假设点源活度为A,在源衬材料足够厚的情况下,反散射的产生几率为εR,如果空气对反散射光子产生衰减,经空气衰减后反散射光子依然存在的概率为εRS,单能放射源的发射几率为Pγ,在空间r处反散射光子依然存在的概率为εS,几何效率乘积为εo,反散射光子注量φR与全能峰光子注量φO在距离r处别分为:
φR=APγεRεRS
(3)
φO=APγεoεS
(4)
因此,r处的反散射与全能峰光子注量之比为:
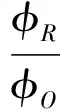
(5)
如果入射到探测器里,由于:

因此测量能谱上解出的反散射光子峰面积与全能峰峰面积之比实际上是r处φR与φO之比再乘以各自能量对应的本征效率之比。记反散射光子能量为ER,探测器对ER的本征效率为εBR,全能峰能量为EO,本征效率为εBO,探测器对两种能量的光子计数分别为nR和nO,则:

(6)
我们在第一部分建立了多源照射器及实验室模型并模拟计算了放射源在实验室内不同位置的能谱。mcnp程序计算粒子输运过程实际就是抽取一个粒子[6,7],然后根据库截面计算粒子在不同位置出现的几率。多源照射器及实验室模型都是真实可验证的,而mcnp计算的粒子探测效率或者说粒子出现几率的问题是相当准确的。
对于干式储藏源,反散射光子产生几率、空气散射后光子的存活率、准直孔多次散射产生的散射光子几率、墙壁散射产生光子的几率等等,这些通过理论公式计算是相当难完成的,mcnp的计数实际已经完全耦合了各种几率,即:
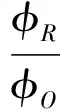
(7)
NR和NO分别为mcnp计算所得反散射计数和主射线计数。
我们在模拟康普顿坪法中求出HPGe探测器本征效率,而全能峰峰面积是标准的高斯峰形,易求解得出,只需要确定测量能谱中反散射峰的左右边界,然后根据全能峰峰面积与反散射峰面积之比就可以得出反散射峰面积,即:
(8)
利用推导法得出反散射与全能峰计数之比实际是相应能区的对应效率之比。而测量能谱中反散射计数nR与全能峰计数nO之比则需要乘上对应的本征效率。由于全能峰计数nO相对易求,便可利用nR与nO之比得出测量谱中的反散射计数。模拟结果为:nR=3995779,nO=1877716,nR/nO=2.218。在既定能区170~220keV范围内,计算得出需整体扣除本底计数为9100。
康普顿坪(此能区可视为常数)扣除示意图见图12,经效率刻度后反散射峰面积为37184601,全能峰面积为409088453。反散射与全能峰计数之比的实验与模拟计算结果比较见表7。
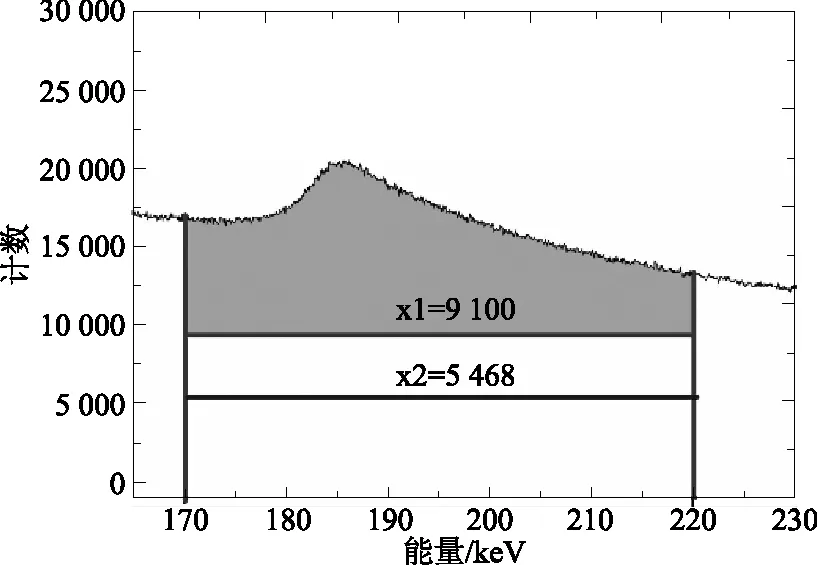
图12 扣除康普顿坪以解析反散射峰面积Fig.12 Excluding Compton Plateau to calculate backscattering peak area

表7 反散射与全能峰计数之比的实验与模拟计算结果比较Table 7 Results comparison of backscattering with full-energy peak count in simulations and experiments
3 结论
本实验对某单位的多源照射器及其实验室建立了三维计算模型,利用该模型理论计算了实验室墙壁对反散射峰计数的影响。实验测量了多源照射器离源不同距离的能谱,证实了干式储藏源的确存在反散射峰。本文采用两种方法扣除测量能谱中的康普顿坪,计算得到所列的干式储藏源反散射与全能峰面积之比分别为0.1261和0.0909。而模拟计算得到此位置的计数之比为0.1055,后者更接近模拟计算结果,相对偏差为-13.8%。模拟计算与实验解谱结果存在较大偏差的原因可能是探测器模型与实际情况有差别。反散射峰康普顿坪的扣除是近似扣除,也是造成较大偏差的一个原因。
[1] Frank Herbert Attix. Introduction to Radiological Physics and Radiation Dosimetry.[M]. Germany:Wiley-VCH,1991:90-120.
[2] 苗亮亮,全林,袁建新,等.校准用γ射线多源照射器研制[C]//第二届全国核技术及应用研究学术研讨会大会论文摘要集,2009.
[3] 全林,朱广宁,苗亮亮,等. 多源照射器屏蔽计算[C]//全国核技术及应用研究学术研讨会, 2009.
[4] Akar Tarim U,N. Ozmutlu E,Gurler O,et al. Monte Carlo analyses of multiple backscattering of gamma rays[J]. Journal of Radioanalytical & Nuclear Chemistry,2013,295(2):901-905.
[5] Sabharwal,D. A,Singh,et al. Investigations of multiple backscattering and albedos of 1.12MeV gamma photons in elements and alloys[J]. Nuclear Instruments & Methods in Physics Research,2009,267(1):151-156.
[6] 许淑艳. 蒙特卡罗方法在实验核物理中的应用[M]. 北京:原子能出版社,2006.
[7] BRIESMEISTER J F. Monte Carlo-N-Particle Transport[R]. LA-13709-M,Los Alamos National Laboratory,2000.
[8] 田自宁,欧阳晓平,殷经鹏,等. BEGe探测器晶体参数的蒙特卡罗计算与实验表征技术研究[J].原子能科学技术,2013,47(8):1411-1417.
[9] 杨东. 航空高纯锗探测器Monte Carlo刻度方法的初步研究[D].北京:中国原子能科学研究院,2005.
TheCalculationofRatiooftheDryStorage137CsSourceBackscatteringPeak
CHENGChang-hao1,YANYong-jun1,QITie-tao1,TUJing2
(1. School of Nuclear Science & Technology,University of South China,Hengyang of Hunan Prov. 421001,China;2. Northwest Institute of Nuclear Technology,Xi’an of Shaanxi Prov.710024,China)
Because of the special structures of the137Cs source,the γ ray emitted by the radioactive source contains backscattering photons. And using this type of storage source in dosimeter’s calibration,there will be some deviations. In this paper,a three dimensional model of the multi-source illuminator is established,which is used to calculate and analyze the effects of the walls to the backscattering counting. Then the137Cs energy spectrum is measured,and two methods to deduct Compton plateau are used to calculate the ratio of the backscattering peak to the full energy peak. The experimental results show that the ratio of backscattering photon at 6 meter in the laboratory to the 661.66keV photon was 0.0909 and the relative deviation was -13.8% between the experimental analysis and the Monte Carlo simulations results.
137Cs source;Backscattering;Dry storage source;Compton plateau
2017-03-30
国家自然科学基金(11575081)
程昌浩(1993—),男,湖北黄冈人,硕士研究生,现从事核技术应用方面研究
颜拥军:yan_jason@163.com
TL812
A
0258-0918(2017)06-0929-07
