基于情景萤火虫算法的机器人路径规划

罗天洪，梁 爽，何泽银，张 霞

(重庆交通大学 机电与车辆工程学院，重庆 400074)

基于情景萤火虫算法的机器人路径规划

罗天洪，梁 爽*，何泽银，张 霞

(重庆交通大学 机电与车辆工程学院，重庆 400074)

针对传统非结构环境下路径规划时机器人运动状态振荡和适应性差等问题，提出了一种基于情景萤火虫算法(SGSO)的机器人路径规划策略。该算法基于混沌系统的规律性、随机性和历遍性以实现初始化，并利用黄金比分割法进行后期优化，以提高种群的多样性，抑制算法的早熟和局部收敛；同时，引入关于萤火虫“天敌”的情景理解，改进萤火虫种群的选择机制，解决萤火虫在非结构环境下寻迹过程中的搁浅现象，增强了算法的适应性和鲁棒性。四个测试函数的仿真实验结果表明，所提算法的求解精度、收敛效率优于基本萤火虫种群优化(GSO)算法；将该算法应用于非结构环境下移动机器人的路径规划中，检测结果表明，基于SGSO的规划路径更短，且转角处更光滑，有效避免了机器人大角度转向对动力系统造成的额外负荷，验证了所提算法的可行性和有效性。

萤火虫群优化算法；路径规划；非结构环境；搁浅现象；移动机器人

0 引言

非结构环境存在表面材质性能不均、结构尺寸变化不规律且不稳定、环境信息非固定或不可知等问题，因此机器人在非机构环境中的路径规划存在较大的难度。现存的算法中人工势场法[1]多被运用到非结构环境规划中的运动，可以实现较低层的实时控制；但该方法易出现局部最优解，并产生死锁现象。因此，亟需一种算法实现移动机器人在非结构环境中的路径规划问题。萤火虫群优化(Glowworm Swarm Optimization, GSO)[2]算法自提出以来被广泛应用于机器人轨迹规划、路径规划和全局分布优化等领域；但该算法存在易陷入局部最优解、早熟、精度低等缺点。现有文献中已有大量分别关于GSO算法或非结构环境下路径规划的研究:郁书好等[3]利用混沌系统的规律性、随机性和遍历性对GSO进行初始化，提高了算法的求解精度及全收敛效率，并成功用于车辆路径问题；Liao等[4]通过对萤火虫的步长选择方式进行修改，调整了萤火虫的分布结构，应用到无障碍环境中传感器分布问题,并有效提高了传感器的覆盖率；Marinaki等[5]提出一种基于空间分布优化的萤火虫算法，通过连续优化的方式解决了存在随机需求车辆的路径规划问题；Zhang等[6]通过对机器人传感器系统进行优化使机器人对障碍物进行感知，并基于力分布应用到对机器人的控制，实现非机构环境下的平稳行走；于乃功等[7]提出了一种基于梯度守恒假设和局部加权对光流的移动机器人避障策略，抑制光照和噪声等变量对其影响，实现非结构环境下的无碰撞行走。此外，文献[8-9]对萤火虫的选择机制进行了优化，提高了萤火虫种群的利用率；文献[10-12]将GSO算法应用到物理和机械领域，验证了GSO算法相比其他智能算法的优点。目前将GSO算法运用到非机构环境下进行路径规划的研究较少。

本文根据非结构环境的特点，提出一种基于情景萤火虫算法(GSO algorithm of Scene understanding, SGSO)的路径规划策略。该算法引入了萤火虫“天敌”的概念，解决萤火虫面对“天敌”时出现的搁浅现象,对萤火虫的选择机制进行影响，保障了求解的精度，降低了传统萤火虫算法早熟和局部收敛的发生概率；同时引入混沌变量与黄金比分割法则优化萤火虫种群，增强在算法在应用过程中的自适应性和鲁棒性。

1 情景萤火虫算法

1.1 情景萤火虫算法原理

GSO算法的原理[10]如下：在多维空间随机分布N个萤火虫个体，每个萤火虫个体带有定量的荧光素li(t)；以概率pij(t)向邻域集合Ni(t)中选取的较优个体移动。计算出适应函数J(xi(t))所对应值，并重复这一过程直到达到一定的迭代次数，得到问题较优解的位置。

GSO算法一个迭代循环如下所示：

(1)

(2)

(3)

(4)

li(t+1)=(1-ρ)li(t)+γ*J[xi(t+1)]

(5)

其中：rs为个体的最大感识半径；β为感识半径变化系数；nt为萤火虫个体附近邻域阈值；Ni(t)为萤火虫个体的邻域集合；s为萤火虫个体移动的步长；ρ为荧光素挥发系数，ρ∈(0,1)；dij(t)为个体i和个体j之间的距离；γ为用于调节函数值的常数量，可以放缩适应度函数J[xi(t+1)]。

与现有的智能群算法相比较，萤火虫算法中需调节的参数简单，且不存在较为繁琐的进化，易于实现，稳定性高；但收敛速度慢、早熟和求解精度不高等缺陷对搜寻最优解造成一定的影响。

1.2 情景萤火虫选择策略

为了增强萤火虫群的搜索能力，拟加入萤火虫的“天敌”，并引入参数暗度di(t)以表示萤火虫对天敌的排斥效果，与基本萤火虫算法中存在荧光素吸引作用共同作用，综合模拟萤火虫在动态环境和未知环境中寻迹的真实过程。

“天敌”对萤火虫选择有抑制作用，参数Oi(t)表示萤火虫邻域内存在的天敌数量，影响萤火虫感识半径的更新，使邻域内萤火虫和天敌共同决定萤火虫的选择机制。

(6)

其中：dii(t)表示萤火虫个体i与感识半径内天敌i所在点之间的距离。为将天敌对于萤火虫路径选择策略的干扰，引入暗度di(t)表示萤火虫个体i邻域内天敌对荧光素传递的抑制效果，暗度di(t)与天敌数量Oi(t)的关系为：

(7)

若萤火虫的感识半径内天敌数量过多或体积过大，萤火虫易停止搜索，因此设最大暗度dmax,防止感识半径减小到0。

由于具备了天敌对萤火虫的刺激作用，个体i向相邻邻域中第j只萤火虫方向移动的概率为：

(8)

加入暗度影响后，选择机制的概率分布从[0,1]扩展到[-1,1]，更利于萤火虫选取最优解。

1.3 情景萤火虫种群的优化

为抑制GSO算法中因为随机初始分布而陷入局部解和早熟收敛的问题，在算法中采用混沌变量[3]作为萤火虫的初始种群，以提高搜索的遍历性、随机性和规律性。前期通过混沌变量进一步提高萤火虫种群的丰富度和收敛速度，后期通过将适应度较低的萤火虫个体进行黄金分割优化，解决萤火虫的“搁浅现象”，保障了求解精度，增强了萤火虫种群初始位置的质量以提高后期收敛效率。

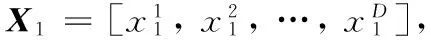
xn+1=cos(narccosxn)

(9)

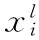
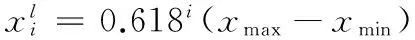
(10)

其中：xmax和xmin分别表示萤火虫个体搜索范围的阈值。

然后通过黄金比分割法则重新分布后的部分个体依式(9)迭代得到xn+1，将经过二次优化后的萤火虫和较高荧光素的种群组成萤火虫的初始种群。

1.4 情景萤火虫算法的描述

情景萤火虫算法总的流程如图1所示，相应步骤描述如下。

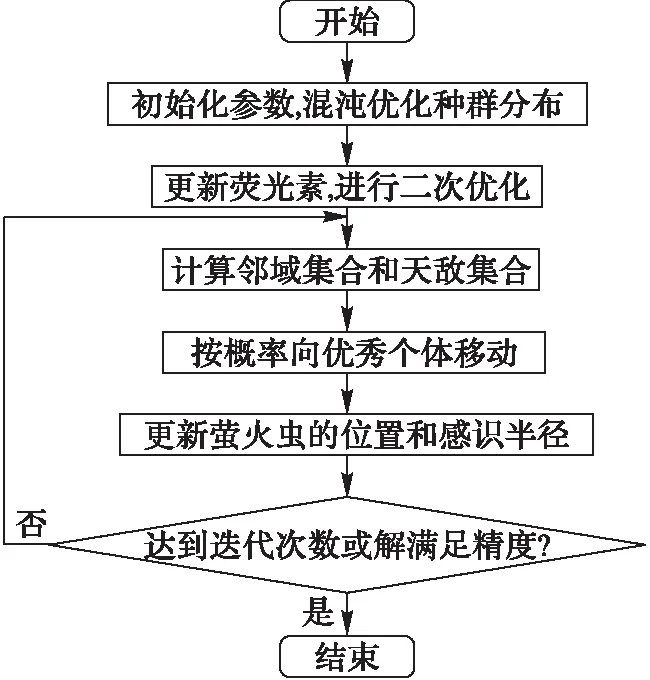
图1 情景萤火虫算法流程Fig.1 Flow chart of SGSO

步骤1 初始化ρ、γ、li(0)及其他常量参数。随机生成D维向量X0=[x0.1,x0.2,…,x0.D]，根据式(9)进行第一次优化，依次得到X1，X2，…，XN，将上述N个混沌向量映射到求解区域内。

步骤2 根据式(5)更新萤火虫种群的荧光素值，筛选出荧光素较低的k个个体，根据式(10)进行二次优化后和一次优化后荧光素较高的部分个体混合组成初始种群。

步骤3 根据式(4)与式(6)分别计算出萤火虫个体i的邻域集合Ni(t)和天敌集合Oi(t)。

步骤4 根据式(8)计算出萤火虫i向邻域内高荧光素个体j移动的概率。

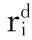
步骤6 判断所求解是否满足条件或者达到最大迭代次数：若满足条件或达到最大迭代次数即输出结果；否则转到步骤3。

2 非结构环境下共融机器人的路径规划

2.1 非结构环境中障碍物的识别和分类

机器人在非结构环境中须通过传感器对工作环境进行感知和识别，提取可能存在的障碍物信息并作出相应的决策以躲避障碍物。为了在复杂工况下保障自身安全，机器人的传感集成系统多包含不同种类的传感器。中央控制系统需将各传感器的信息输入进行融合以及处理，为机器人的运动进行规划。

非结构环境下障碍物分布不规律、体积不规则，而障碍物的随机性往往对移动机器人的运动性能造成影响。因此，对于不同种类障碍物，机器人根据其特点作出相应的避障决策，从而达到路径规划的目的。障碍物的分类如表1所示。

表1 非结构环境中常见障碍物分类Tab. 1 Common obstacle classification in unstructured environment

2.2 非结构环境下路径规划的情景理解

传统路径规划的算法在建立模型的过程中，障碍物和机器人的外型通常经过结构化或其他简化处理，为考虑实际运动过程中由体积因素可能带来的碰撞或冲击等不利工况，为了细致地描述环境的特点，更为精确地在算法中模拟障碍物的分布情况，本文算法在确定环境参数的过程中需增加机器人与障碍物的体积对路径的影响，以再现运动过程中机器人和障碍物之间相对位置关系。

通过关于障碍物各参数的收集与处理，分析机器人可识别范围内障碍物体积等可增益变量的影响范围，量化各类障碍物对于机器人路径选择策略的影响因子，实现对于障碍物的膨胀保护，保证机器人在运动过程中的安全。

(11)

其中：α表示机器人识别障碍物的展角，rk1表示障碍物k到传感器最短的距离，rk2表示感知范围内障碍物k到传感器最远的距离，G表示障碍物量化增益系数。根据式(11)对萤火虫个体感知范围内的障碍物进行识别和量化。

由于非结构环境具有未知性和不确定性，且目前传感器的测量与分析水平有限，实际环境中的障碍物和理想模型中的传感器必然存在一定的误差。为避免上述测量误差可能引起的碰撞与跌落现象，引入安全系数s以确保机器人与障碍物之间始终保持一定的间隙，从而保障寻迹过程的稳定性。其中s∈[1.05，1.20]。当环境中障碍物数量较少时，选取较小的安全系数，以减少机器人的移动路径；当环境中障碍物数量较多时，选取较大的安全系数，以保障运动过程中的无冲撞[13]。

2.3 非结构环境下路径规划的目标描述

非结构环境下的路径规划就是确定移动机器人从出发点到目标点所经过m+1个点的集合[13]，由于非结构环境的障碍存在不确定的因素，机器人的移动路径应适应于存在各种障碍的环境，因此模型的建立必须不依赖障碍物的任何参数。如图2所示，以机器人的出发点O与目标点Pm的连线建立X轴，过出发点O且垂直于X轴的直线作为Y轴，建立全局坐标系O-XY。然后将OPm等分成m段，并过每一个等分点作垂线,从而的到垂线族(h1,h2,…,hm-1)，而各垂线与路径的交点即为路径中部分必须经过的目标点(P1,P2,…,Pm-1)。在不影响结果的前提下，为减小计算量，且便于观察，将X轴进行平移后提取出新的坐标系。通过上述策略将移动机器人的路径规划转变为一系列目标点的选取过程。

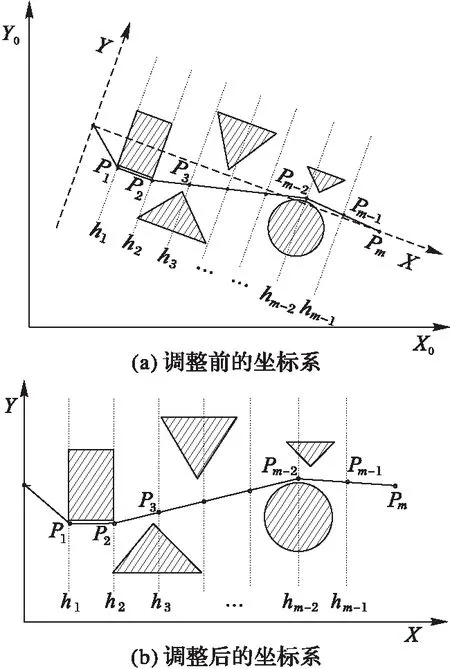
图2 路径规划过程Fig. 2 Process of path planning

为了减小能量的消耗，机器人从起点到终点所经历总路程应尽量短，即要满足函数L取最小值。

(12)

其中：LOP1表示点O到点P1间的距离，LPjPj+1表示点Pj到Pj+1间的距离。也可以用坐标表示式(12)为：

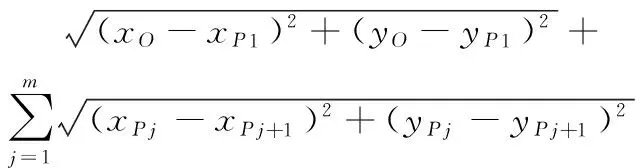
(13)

最终机器人的路径规划转化为对于式(13)的函数在取值范围内寻找最小的函数值Lmin。通过多次目标转换，使模型的目标锁定为最短路程，且适应于非结构环境下障碍物随机分布的特点。

3 算法性能分析

为了进一步验证SGSO的有效性，将SGSO与GSO算法、混沌GSO(Chaotic GSO, CGSO)进行性能对比。为方便对比，选取参考文献[3]中基准测试函数分布进行对比测试。首先对各参数进行初始化，如表2所示。

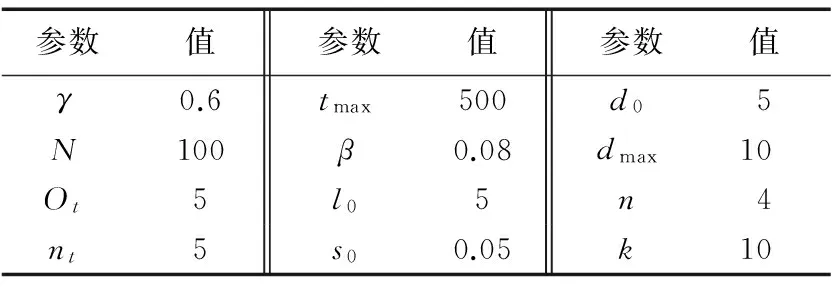
表2 SGSO与GSO算法的初始化参数Tab. 2 Initialization parameters of SGSO and GSO algorithms

具体函数如下：

f1=(|x1|-5)2+(|x2|+5)2；xi∈[-10,10]，i=1,2

该函数的全局最小值为25。

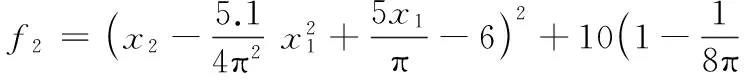
x1∈[-5,10],x2∈[0,15]

该函数的全局最优值为0.397 898。

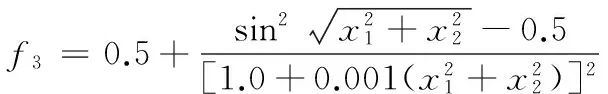
x1∈[-5,10],x2∈[0,15]

该函数的全局最小值为0。

f4=100(x2-x1)2+[6.4(x2-0.5)2-x1-0.6]2；

xi∈[-5,5]；i=1,2

该函数的全局最小值为0。

由于单次实验结果不具有代表性，分别通过GSO算法和SGSO对上述测试函数进行100次运行，并提取出结果中的各项值，如表3。

从表3中的数据可以看出：求解精度方面，通过SGSO所得到4个函数的最差值和平均值皆优于GSO算法和CGSO算法，但函数f3和f4的最优值精度不如CGSO算法；通过GSO算法得出函数f1的最优值与最差值与标准值的差值分别为5.654 9×10-3和3.719 6，而通过SGSO的对应值分别为4.512 3×10-6和1.283 894×10-4，其误差值相比减小到原来的1/29 060和1/1 253。稳定性方面，SGSO的标准偏差值均低于GSO算法和SGSO，其中，通过SGSO得到函数f3的标准偏差相对GSO算法和SGSO的进一步优化程度较小，但仍提高23%。收敛效率方面，从图3可以看出，SGSO的收敛曲线中拐点出现较早，都出现于100次迭代之前，收敛速度明显快于GSO算法；种群分布方面，从图4可以看出，在函数f1和f3中，SGSO中萤火虫种群收敛于在最优解的附近，说明改进后的SGSO情景理解模式和选择机制提高了算法的求解性能。综上所述，SGSO求解精度较高，稳定性良好，种群分布合理性强，收敛速度快。

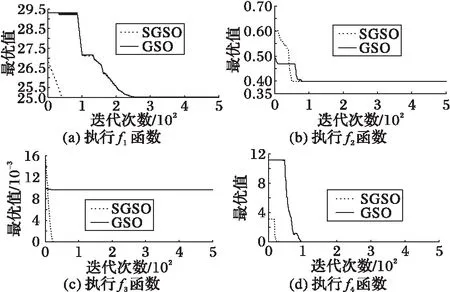
图3 不同算法执行f1～f4函数收敛对比Fig. 3 Convergence comparison of f1-f4 functions implemented by different algorithms

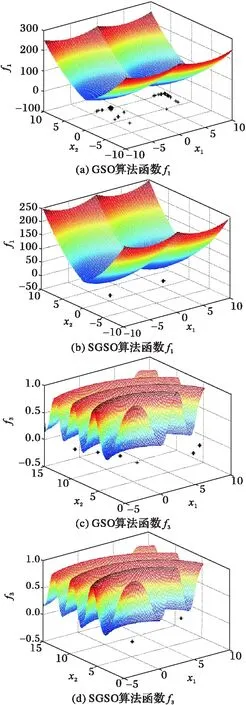
图4 不同算法函数f1、 f3萤火虫最终分布Fig. 4 Glowworm final distribution of f1, f3 with different algorithm表3 GSO、CGSO与SGSO函数求解结果Tab. 3 Functional test results of GSO, CGSO and SGSO

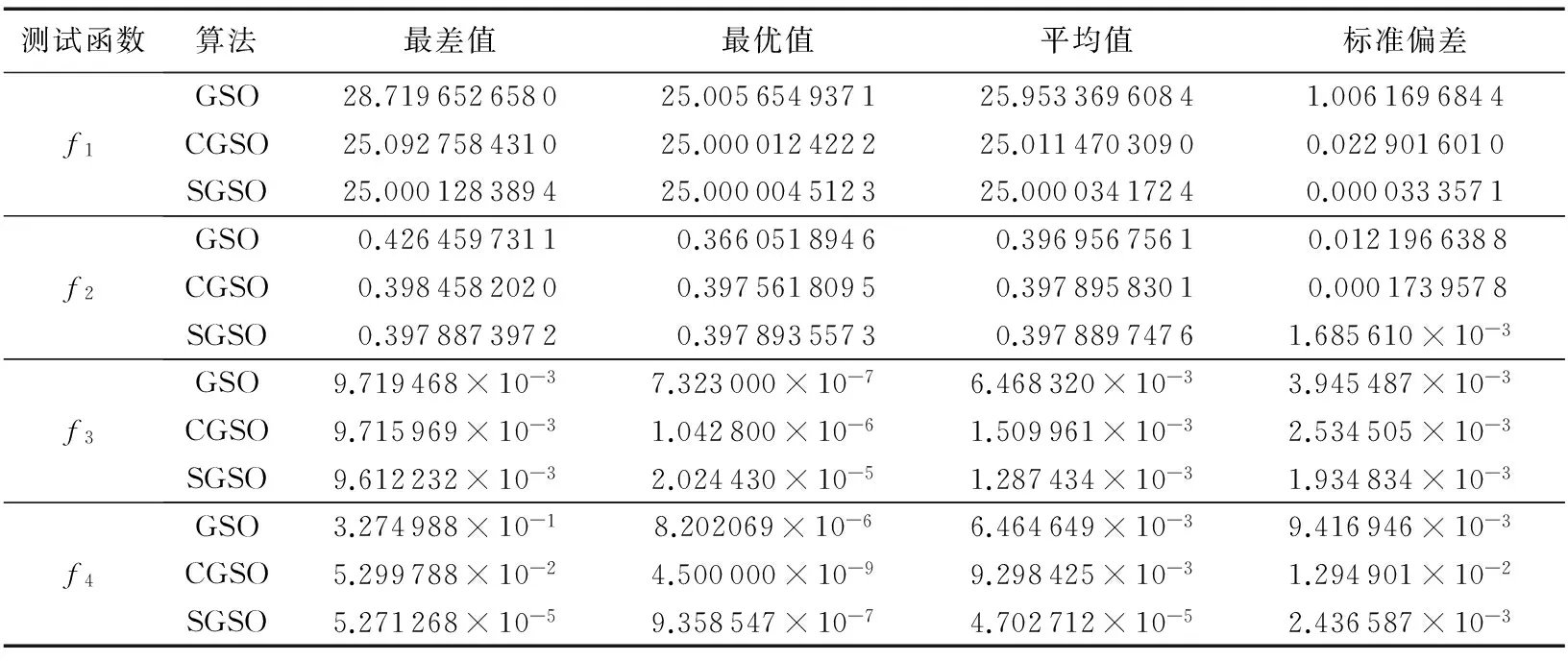
测试函数算法最差值最优值平均值标准偏差f1GSO28.719652658025.005654937125.95336960841.0061696844CGSO25.092758431025.000012422225.01147030900.0229016010SGSO25.000128389425.000004512325.00003417240.0000333571f2GSO0.42645973110.36605189460.39695675610.0121966388CGSO0.39845820200.39756180950.39789583010.0001739578SGSO0.39788739720.39789355730.39788974761.685610×10-3f3GSO9.719468×10-37.323000×10-76.468320×10-33.945487×10-3CGSO9.715969×10-31.042800×10-61.509961×10-32.534505×10-3SGSO9.612232×10-32.024430×10-51.287434×10-31.934834×10-3f4GSO3.274988×10-18.202069×10-66.464649×10-39.416946×10-3CGSO5.299788×10-24.500000×10-99.298425×10-31.294901×10-2SGSO5.271268×10-59.358547×10-74.702712×10-52.436587×10-3

4 SGSO在危桥检测路径规划的应用

本文针对的非结构环境为存在隐患的危桥部分桥面，其模型参数为：截取部分长度L1=8 m，宽度L2=6 m，桥面随机存在5到9个位置未知、尺寸未知的障碍。为验证本文算法不受障碍物分布的随机性的影响，选取6次不同障碍分布的情景分别进行路径规划。机器人出发点的坐标为(0,3)，计算机器人移动到目标点(8,3)的路径。通过SGSO对目标函数进行100次优化，在100次优化结果中移动路径的各类值，从而得出路径规划的最优解。

图5是SGSO在6类不同障碍分布的危桥桥面路径规划结果。图5(a) ～(b)中分别随机分布了5个障碍物，代表障碍物较少的桥面，结合表4的数据，与GSO算法相比，SGSO的平均路径分别缩短了0.97%和1.8%；图5(c) ～(d)中分别随机分布了7个障碍物，代表障碍物较多的桥面，平均路径分别缩短了1.2%和1.7%；图5(e) ～(f)中代表含陷阱障碍物，平均路径分别缩短了1.9%和2.2%，避开陷阱的成功率为100%。此外，GSO算法生成的路径在靠近圆形或椭圆形时距离障碍物较近，而靠近直角或锐角障碍时较远；SGSO生成路径距离各类障碍的距离具有较好的一致性。

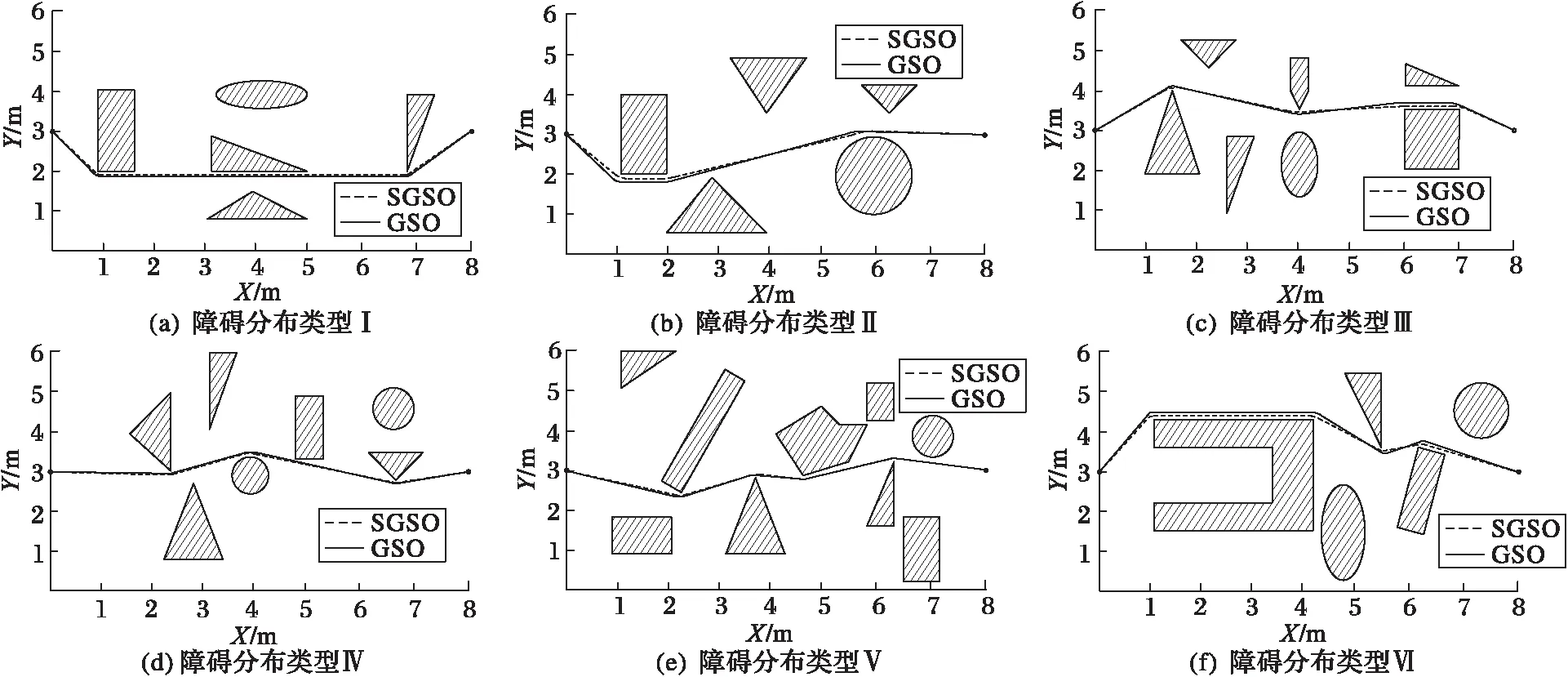
图5 不同障碍分布类型下不同算法路径规划结果Fig. 5 Path planning results of different algorithms under different obstacle distribution types

传统路径规划中机器人的移动路径多与障碍物相切，本文模型建立的过程中加入了安全系数，优化后的路径与障碍物之间保持了一定的间隙，该方式使移动距离略有增加，但极大地降低了与障碍物冲撞的概率，提高了运动过程的安全性。为进一步观察SGSO关于运动效率与避障能力的兼顾性，选取了两处含尖锐障碍物的局部细节图，以观察SGSO的路径规划表现，如图6所示。从图6中可以看出来，相比通过GSO算法，通过SGSO所生成的路径在拐点处与障碍物所保持的距离更加稳定，且路径具备更好的光滑度，减小了机器人过弯的转角调整，有利于避免机器人运动状态振荡。

图6 不同障碍物分布类型下局部路径细节Fig. 6 Local paths details under under different obstacle distribution types

由于模型的建立不受障碍的位置、性质的影响，GSO算法和SGSO皆可以在障碍物随机分布的桥面完成移动机器人的路径规划。通过数据对比，SGSO的求解精度和迭代稳定性皆高于GSO算法。

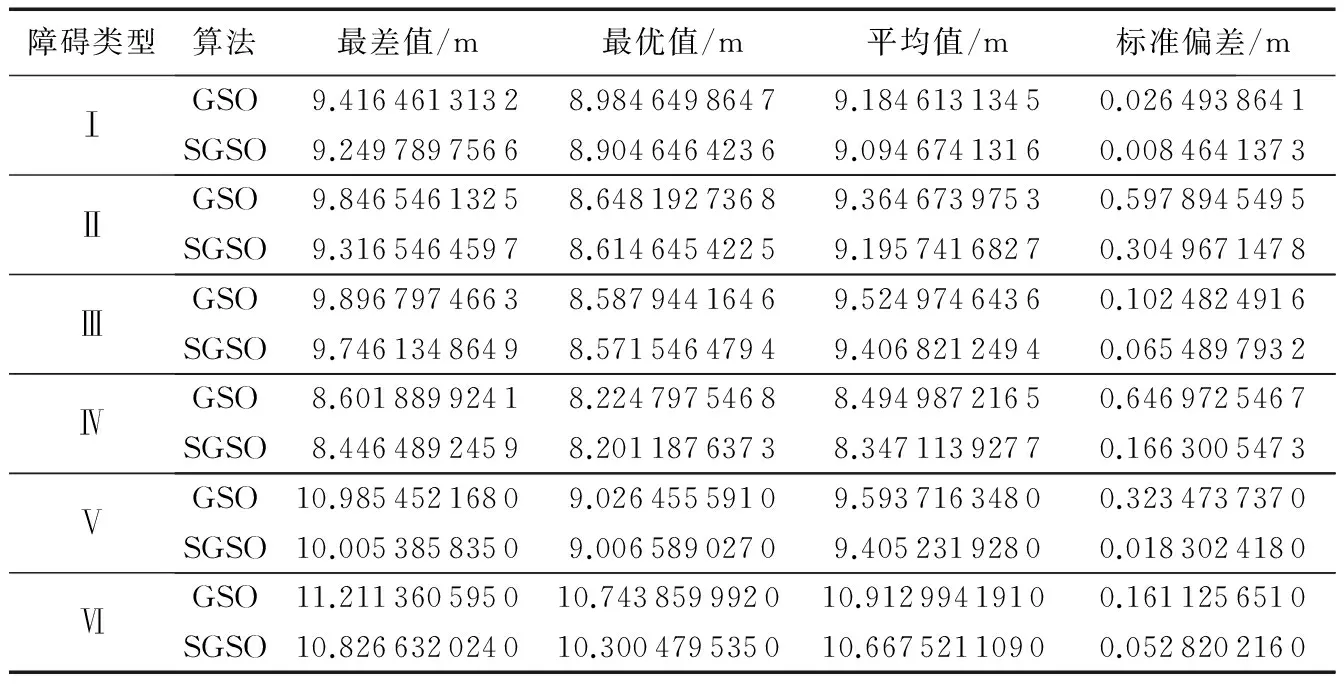
表4 GSO与SGSO算法路径规划结果Tab. 4 Path planning results of GSO and SGSO algorithms

5 结语

为克服传统萤火虫算法易陷入局部最优解、早熟、精度低等缺点，本文提出情景萤火虫算法(SGSO)，用于在非环境结构下为移动机器人提供可行的路径规划策略。该算法基于混沌映射的历遍性、随机性和规律性实现种群初始化，通过黄金比分割法优化提高种群的多样性和机动性，并引入萤火虫“天敌”的情景理解改善个体的选择阈值和精度，进化萤火虫的选择机制。通过标准函数的仿真实验及对比分析可知，SGSO比GSO算法及同类算法具备更高的求解精度、稳定性和迭代效率，种群的最终分布位置均收敛于最优解附近；危桥检测应用的结果也验证了所提算法的可行性和有效性。

实际的非结构环境具备更多不确定性，下一步将在建模的过程中考虑传感器的时滞性、测量过程的非线性误差以及边界条件的变化，进一步探索SGSO在非结构环境中的理论研究和应用意义。

References)

[1] LI C, JIANG X, WANG W, et al. A simplified car-following model based on the artificial potential field [J]. Procedia Engineering, 2016, 137: 13-20.

[2] KRISHNANAND K N, GHOSE D. A glowworm swarm optimization based multi-robot system for signal source localization [M]// Design and Control of Intelligent Robotic Systems. Berlin: Springer, 2009: 49-68.

[3] 郁书好,苏守宝.混沌萤火虫优化算法的研究及应用[J].计算机科学与探索,2014,8(3):352-358.(YU S H, SU S B. Research and application of chaotic glowworm swarm optimization algorithm [J]. Journal of Frontiers of Computer Science and Technology,2014, 8(3): 352-358.)

[4] LIAO W H, KAO Y C, LI Y S. A sensor deployment approach using glowworm swarm optimization algorithm in wireless sensor networks [J]. Expert Systems with Applications, 2011, 38(10): 12180-12188.

[5] MARINAKI M, MARINAKIS Y. Glowworm swarm optimization algorithm for the vehicle routing problem with stochastic demands [J]. Expert Systems With Applications, 2016, 46(C): 145-163.

[6] ZHANG H, LIU Y B, ZHAO J, et al. Development of a bionic hexapod robot for walking on unstructured zerrain [J]. Journal of Bionic Engineering, 2014, 11(2): 176-187.

[7] 于乃功,郑宇凌,徐丽,等.基于光流的非结构化环境中移动机器人避障方法[J].北京工业大学学报,2017,43(1):65-69.(YU N G, ZHENG Y L, XU L, et al. Optical flow based mobile robot obstacle avoidance method in unstructured environment [J]. Journal of Beijing Universityof Technology, 2017, 43(1): 65-69.)

[8] 刘佳,梁秋丽,王书青,等.基于模拟退火算法的萤火虫群优化算法研究[J].计算机仿真,2014,31(5):284-288.(LIU J, LIANG Q L, WANG S Q, et al. Research on improved glowworm swarm optimization algorithm based on simulated annealing algorithm [J]. Computer Simulation, 2014, 31(5): 284-288.)

[9] ORAMUS P. Improvements to glowworm swarm optimization algorithm [J]. Computer Science, 2010, 11: 7-20.

[10] 罗天洪,陈才,李富盈.基于时变萤火虫群算法的冗余机器人手臂逆解[J].计算机集成制造系统,2016,22(2):576-582.(LUO T H, CHEN C, LI F Y. Inverse solution of redundant robot arm based on glow-worm swarm optimization algorithm of time-varying [J]. Computer Integrated Manufacturing Systems, 2016, 22(2): 576-582.)

[11] DING S, AN Y, ZHANG X, et al. Wavelet twin support vector machines based on glowworm swarm optimization [J]. Neurocomputing, 2017, 225(C): 157-163.

[12] CUI H, FENG J, GUO J, et al. A novel single multiplicative neuron model trained by an improved glowworm swarm optimization algorithm for time series prediction [J]. Knowledge-Based Systems, 2015, 88(C): 195-209.

[13] 孙波,陈卫东,席裕庚.基于粒子群优化算法的移动机器人全局路径规划[J].控制与决策,2005,20(9):1052-1055,1060.(SUN B, CHEN W D, XI Y G. Particle swarm optimization based global path planning for mobile robots [J]. Control and Decision, 2005, 20(9): 1052-1055, 1060.)

This work is partially supported by the National Natural Science Foundation of China (51375519).

LUOTianhong,born in 1975, Ph.D., professor. His research interests include robotics, mechatronics.

LIANGShuang, born in 1993, M. S. candidate. His research interests include robot dynamics and system control.

HEZeyin, born in 1985, Ph. D.,associate professor. His research interests include mechanical design and theory, mechanical reliability analysis.

ZHANGXia,born in 1982, Ph. D., associate professor. Her research interests include robot control method and theory, exoskeleton motion assisted robot.

Pathplanningofrobotbasedonglowwormswarmoptimizationalgorithmofsceneunderstanding

LUO Tianhong, LIANG Shuang*, HE Zeyin, ZHANG Xia

(SchoolofMechanotronicsandVehicleEngineering,ChongqingJiaotongUniversity,Chongqing400074,China)

Against at the problems of oscillation and poor adaptability of robot motion state in the path planning of traditional unstructured environment, a new path planning strategy based on Glowworm Swarm Optimization algorithm of Scene understanding (SGSO) was proposed. The initialization was realized based on the regularity, randomness and generalization of chaotic systems, and golden section method was used for later optimization, which improved the diversity of the population, suppressed the premature and local convergence of the algorithm. And, by introducing scene understanding of glowworm “natural enemy”, the selection mechanism of glowworm swarm was optimized to solve the grounding phenomenon of glowworm in the process of tracing under unstructured environment, which enhanced the adaptability and robustness of the algorithm. The simulation results of four test functions show that, the proposed algorithm is superior to the basic Glowworm Swarm Optimization (GSO) algorithm in solving precision and convergence efficiency. The proposed algorithm was applied to the path planning of mobile robots in unstructured environment, the test results show that the planning path based on SGSO was shorter and the corner was more smooth, which could effectively avoid the additional load on power system caused by large angle steering of robot, verifying the feasibility and effectiveness of the proposed algorithm.

Glowworm Swarm Optimization (GSO) algorithm; path planning; unstructured environment; grounding phenomenon; mobile robot

2017- 05- 08;

2017- 06- 20。

国家自然科学基金资助项目(51375519)。

罗天洪(1975—)，男，四川乐至人，教授，博士，主要研究方向：机器人、机电一体化； 梁爽(1993—)，男，重庆人，硕士研究生，主要研究方向：机器人动力学与系统控制； 何泽银(1985—)，男，四川遂宁人，副教授，博士，主要研究方向：机械设计及理论、机械可靠性分析；张霞(1982—)，女，重庆铜梁人，副教授，博士，主要研究方向：机器人控制方法与理论、外骨骼运动辅助机器人。

1001- 9081(2017)12- 3608- 06

10.11772/j.issn.1001- 9081.2017.12.3608

(*通信作者电子邮箱137377539@qq.com)

TP391.9;TP242

A