马尔可夫随机场的空间相关模型在非负矩阵分解线性解混中的应用

袁 博

(南阳理工学院 计算机与信息工程学院，河南 南阳 473004)

马尔可夫随机场的空间相关模型在非负矩阵分解线性解混中的应用

袁 博*

(南阳理工学院 计算机与信息工程学院，河南 南阳 473004)

针对基于非负矩阵分解(NMF)的高光谱解混存在的初始化与“局部极小”等问题，提出一种基于马尔可夫随机场(MRF)的空间相关约束NMF线性解混算法(MRF-NMF)。首先，通过基于最小误差的高光谱信号识别(HySime)法估算端元数量，同时利用顶点成分分析(VCA)和全约束最小二乘法(FCLS)初始化端元矩阵与丰度矩阵；其次，利用MRF模型建立描述地物空间分布规律的能量函数，以此描述地物分布的空间相关特征；最后，将基于MRF的空间相关约束函数与NMF标准目标函数以交替迭代的形式参与解混，得出高光谱数据的端元信息与丰度分解结果。理论分析和真实数据实验结果表明，在高光谱数据空间相关程度较低的情况下，相比最小体积约束的NMF(MVC-NMF)、分段平滑和稀疏约束的NMF(PSNMFSC)和交互投影子梯度非负矩阵分解(APS-NMF)三种参考算法，所提算法的端元分解精度仍分别提高了7.82%、12.4%和10.1%，其丰度分解精度仍分别提高了8.34%、12.6%和9.87%。MRF-NMF能够弥补NMF对于空间相关特征描述能力的不足，减小解混结果中地物的空间能量分布误差。

非负矩阵分解；高光谱线性解混；空间相关；马尔可夫随机场; 交替迭代；空间能量

0 引言

“混合像元”是影响高光谱定量遥感应用精度的关键问题之一。随着高光谱数据应用领域的不断拓展及应用精度要求的不断提高，各种解混方法层出不穷。其中，文献[1]提出的非负矩阵分解(Non-negative Matrix Factorization, NMF)技术由于适合处理高维数据，且排除了无意义的负值元素，形式上类似于线性光谱混合模型，使得基于NMF的解混算法成为高光谱线性解混研究中的热点。

由于存在初始化、“非凸”导致“局部极小”等问题，标准NMF的解混效果并不理想，大量用于高光谱解混的NMF扩展方法不断涌现。这些方法的共同特点在于：通过在标准NMF目标函数内部加入描述某种高光谱图像典型特征的约束项，达到缩小解空间、加快迭代并提高解混精度等目的。例如，文献[2]提出了一种基于NMF的光谱解混算法，向标准NMF算法中加入了端元光谱的平滑性和丰度的稀疏性约束；文献[3]提出了最小体积约束的NMF(Minimum Volume Constrained NMF, MVC-NMF)算法；文献[4]提出了交互投影子梯度非负矩阵分解(NMF with Alternating Projected Subgradients, APS-NMF)；文献[5]也提出了分段平滑和稀疏约束的NMF(Piecewise Smoothness NMF with Sparseness Constraints, PSNMFSC)，但需要预先指定稀疏度。

上述NMF扩展方法的共同问题在于：首先，仅将高光谱数据视为各类光谱信息或统计信息的集合，忽略了空间属性，特别是各地物(端元)类型之间显著的空间相关特征；其次，扩展后的目标函数往往包含多个内部函数项，容易产生相互干扰。上述两点在不同程度上制约了高光谱解混精度的进一步提高。

近年来，基于空间相关特征的高光谱解混研究也取得了大量学术成果。例如，文献[6]提出了一种基于图正则化的半监督NMF算法(Graph regularized-based Semi-supervised NMF, GSNMF)，克服了NMF忽略样本数据局部几何结构的缺陷；文献[7]利用训练数据构造结构化字典，添加空间相关性约束项和训练数据的空间信息，提出了一种新的高光谱解混方法；文献[8]利用先验概率密度函数表达两个相邻区域的空间相关程度，提出了一种区域相关的NMF解混算法；文献[9]提出了一种基于稀疏约束和图正则化的半监督NMF方法，在进行低维非负分解时，能够保持数据几何结构。

上述算法需要大量先验知识，对于部分先验知识不足或难以实地获取的真实高光谱数据来说，算法精度与应用效果受到一定制约。针对上述问题，本文提出一种基于马尔可夫随机场 (Markov Random Field, MRF)模型的NMF线性解混算法(NMF linear unmixing algorithm based on MRF, MRF-NMF)。MRF-NMF可归类为非监督算法，对先验知识依赖程度低，利用NMF实现高光谱数据的线性解混并保证基本的解混精度，通过引入MRF模型描述高光谱图像的地物空间相关特征，修正NMF标准目标函数产生的解混误差，进一步改善解混精度。

1 基于MRF模型的NMF解混

由于具有二维空间图像属性，高光谱遥感图像在包含大量光谱信息和统计信息的同时，也含有丰富的空间信息。例如，自然地物的空间分布具有成片、连续的特点，导致高光谱图像中邻近像元取值相近，且端元的空间分布具有连续性和相关性。

高光谱图像的空间能量大小由地物的空间变化频率和幅度决定，频率越低、幅度越小，则空间能量越小。由于端元的空间相关性，决定了局部邻域内端元变化地频率低、幅度小，即理想的NMF分解结果中，端元的“空间能量”应尽可能小。因此，一般情况下度量空间能量大小的能量函数取值越小，越接近地面真实情况。

文献[10]指出，如果NMF解混方法没有考虑邻近地物间的相似关系，忽略了端元分布的空间相关性，解混结果中端元分布受到其他类型端元或噪声的干扰程度就高，容易导致端元“空间能量”偏大，亦即端元在各混合像元中的分布比例失真程度偏大，影响解混精度。

为解决上述问题，需要构建一种描述端元分布空间相关性的模型，使解混过程中端元分布“空间能量”不断向理想状态(最小)靠近，提高结果中端元空间分布与地面真实情况的符合程度。

1.1 MRF模型

MRF模型是根据像元局部空间相关性建立其联合概率分布的一种有力工具，其最大优点在于既能利用像元本身的特征信息，又能利用相邻像元之间的相关信息。设x={x1,x2,…,xB}是随机变量簇X={X1,X2,…,XB}的一个实现，所有可能的实现组成一个空间T，N={Nt,t∈T}为定义在T上的邻域系统，若随机场X满足条件(1)，则称X是以N为邻域系统的MRF：

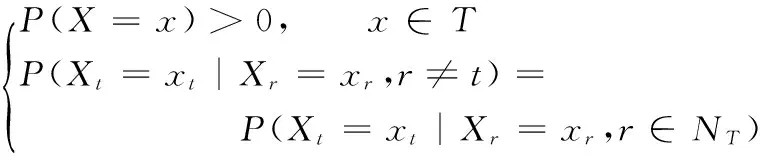
(1)

MRF模型能够提供关于高光谱图像的一种统计描述，很好地体现出每个像元关于其邻近像元的条件分布(亦即端元分布的空间相关程度)，而该条件分布即表现为MRF的局部特性。当邻域系统阶数足够大，任何定义在T上的高光谱图像均可看成是MRF的一个实现。

1.2 描述地物空间相关特征的MRF模型

由于MRF的定义没有明确给出联合概率的具体形式，使用起来很不方便。根据文献[11], Hammersley-Clifford定理建立了MRF和Gibbs随机场之间的等效性，将MRF模型的最优解问题转化为求解Gibbs随机场能量函数的最小值问题。

不同的能量函数形式可构造出不同的MRF模型，较常见的MRF模型有自生模型(Auto Model)和多级逻辑模型(Multi-Level Logistic, MLL)等。本文采用Deng等[12]提出的MRF模型来描述端元空间相关性，该模型将能量函数分为两部分，如式(2)所示：

E=ER+EF

(2)

式中：EF是表示图像本身特征的能量函数，只和观测值分布有关，如式(3)所示；ER是表示像元与邻域相关性的能量函数。

(3)

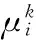
(4)

式中：P为端元数；当x=xi+r时，δ(x,xi+r)=-1，否则δ(x,xi+r)=0；c表示邻域模型的阶数。

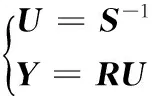
(5)

将式(5)代入式(2)～(4)，设W为全部像元对应特征向量的均值矩阵，可推出以U为自变量的MRF模型能量函数E(U)，如式(6)所示：

E(U)=ER(U)+EF(U)=

(6)

如前文所述，由于能量函数E(U)取最小值时， MRF模型描述的“空间能量”最小，空间分布情况最理想。因此，对式(6)关于U求导，经过化简得到最终结果如式(7)所示：

U=(RT·R)-1·(W·R)T

(7)

1.3 MRF-NMF模型

MRF-NMF通过NMF和MRF交替运行的方式计算分离矩阵U。其中，NMF步骤选择基于欧氏距离的标准目标函数(8)作为保证解混精度的基础；迭代规则选择最大似然法，得到的端元光谱矩阵和丰度矩阵的乘性迭代公式分别为式(9)和式(10)。

(8)

(9)

(10)

MRF步骤中，利用1.2节中的能量函数模型及相关公式，对NMF解混结果中的端元分布情况进行修正，使其逐步向“空间能量”最小的理想分布状态逼近。

综上所述，MRF-NMF算法步骤可简单归纳如下：

整地，首先对地面杂物清理，清除杂草，保证苗圃地的清净；其次对高洼地面采用推土机进行平整，将土层较厚的土壤推到低洼的地方。

1)利用基于最小误差的高光谱信号识别(Hyperspectral Signal identification by minimum error, HySime)法估算端元数量P；

2)基于估算出的端元数量P，结合顶点成分分析(Vertex Component Analysis, VCA)和全约束最小二乘法(Fully Constrained Least Square, FCLS)，初始化端元矩阵M和丰度矩阵S；

3)NMF步骤：利用标准NMF方法进行迭代运算，得到分离矩阵U的迭代结果；

4)MRF步骤：归一化U的每一列，同时估计像元对应特征向量的均值矩阵W，然后利用式(7)计算U；

5)重复步骤3)～4)，直到各自的停止准则同时满足，得到一个估计的成分，将其转换为矩阵，即获得一个端元分布。继续迭代，直至满足阈值条件，得到端元分布的估计结果。

步骤1)中采用的端元数量估计算法(HySime)，是一种估计高光谱信号子空间的方法，虽然计算过程复杂，但不需任何参数，具有自适应性，估计准确度较高。文献[13]给出了该算法的原理与详细实现过程。

步骤2)中用于初始化端元矩阵的VCA是一种端元识别算法，优点是运行时间短、效率高、精度较高，缺点是对纯像元比较依赖。但文献[14]实验结果表明，即使纯像元不存在，VCA作为NMF的端元初始化算法的精度与综合性能也是比较理想的。

从步骤3)和4)可以看出，MRF-NMF摒弃了在NMF目标函数内部添加新约束项的传统做法，通过MRF构建与NMF目标函数交替运行的独立辅助函数，避免了内部函数项之间的相互干扰。

下面讨论该算法的收敛性。

2 实验结果与分析

实验运行的软硬件环境：操作系统Windows 7 Service Pack 1 64 b；处理器Intel Xeon E3- 1230 v3 3.30 GHz；内存8.00 GB；硬盘Seagate 1 TB 7 200 rpm。

本文根据文献[17]计算全局Moran’I指数，定量描述实验数据的空间相关程度，采用了两组空间相关程度不同的真实高光谱数据进行解混实验。全局Moran’I指数越高，表示图像空间相关程度越高，反之则越低。

2.1 真实数据实验1

实验数据1选择美国华盛顿特区的机载高光谱数字图像收集实验仪器(HYperspectral Digital Imagery Collection Experiment, HYDICE)获取的高光谱图像，如图1所示。该数据的全局Moran’I指数为0.498 6，说明其空间相关程度较高。图像行列数均为400，具有明显的地物分布空间相关性；原始波段数量210，波段范围0.4～2.4 μm，波段宽度为10 nm，涵盖了可见光和近红外谱段范围；在去除了0.9～1.4 μm范围内的大气吸收波段后，剩余191波段。

图1 美国华盛顿特区HYDICE数据伪彩色图像(R:60，G:25，B:15)Fig. 1 Pseudo-color image of HYDICE data in Washington, DC, USA (R:60，G:25，B:15)

通过目视解译，图像中主要含有植被、裸土、水体3种地物，其他类型地物还包括线状道路、小型建筑物等。为简化描述，实验中不考虑面积比例很小的地物类型，即认为所有像元中都只包含植被、裸土、水体3种主要地物。

由于HYDICE为机载光谱成像仪，空间分辨率高，可认为图像中每种端元都含有大量纯像元。因此，本文通过在原图像中人工选择参考点的方式收集每种端元(地物)的光谱作为参考值，利用全约束最小二乘法计算端元的丰度参考值。其中，得到的端元参考光谱如图2所示。由图2可以看出，相对其余两种地物，水体的光谱曲线差异最为显著。由于实验数据为遥感影像像元亮度(Digital Number, DN)值，且缺少进行反射率反演的必要参数，图2中光谱曲线的y轴数值为DN值，而非地表反射率。

接下来，通过均值法重采样使图像的空间分辨率降低为原来的0.1倍，由于空间分辨率的大幅降低，形成了大量混合像元。然后，对生成的含有大量混合像元的新图像进行解混实验，以验证本文算法的效果和精度。由于在地物范围确定的前提下，丰度分解结果的尺度是和空间分辨率大小严格对应的，这里同样利用均值法重采样技术把之前求出的端元丰度参考值进行聚合，得到行、列元素数量均为原始图像0.1倍的新图像的丰度参考值，作为解混结果精度分析中的近似真值。重采样后对应的丰度参考值如图3所示。

需要说明的是，图3中纯白色代表端元在该像元内部面积比例为1(100%)，纯黑色代表端元在该像元内部面积比例为0，其余各阶灰度分别对应0～1的不同比例。下文其他丰度图像中，不同灰度代表的含义与图3相同。

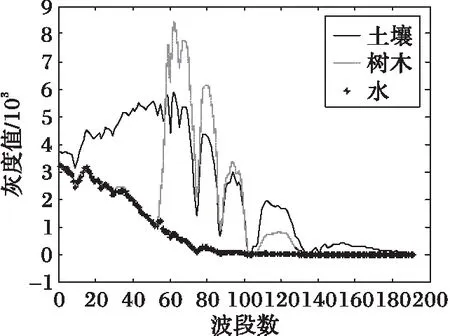
图2 HYDICE数据端元参考光谱Fig. 2 Endmember reference spectrum of HYDICE data

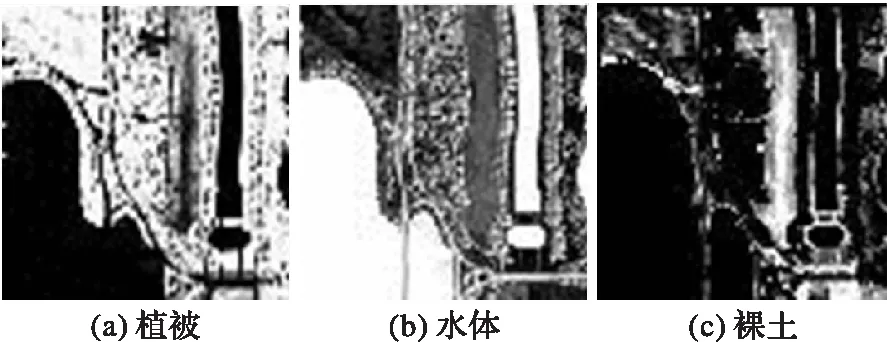
图3 HYDICE数据丰度参考值Fig. 3 Abundance reference value of HYDICE data

为充分展示本文方法在解混真实高光谱图像时的效果，选择前文提到的三种比较有代表性的NMF解混算法MVC-NMF、PSNMFSC和APS-NMF作为参考算法，与MRF-NMF进行实验对比。与本文算法类似，MVC-NMF等三种算法均以不同的原理与形式，在NMF解混过程中引入了高光谱图像的空间信息，且文献[3～5]表明，三种解混算法均有效且具有较为理想的精度。

MRF-NMF丰度分解结果如图4所示，其中三幅子图中的白色分别代表了某种地物类型在图像中的分布位置。由图4可以看出，三者与图3中分别对应的真值基本吻合，说明MRF-NMF能够将三种不同光谱特征的地物有效分离。

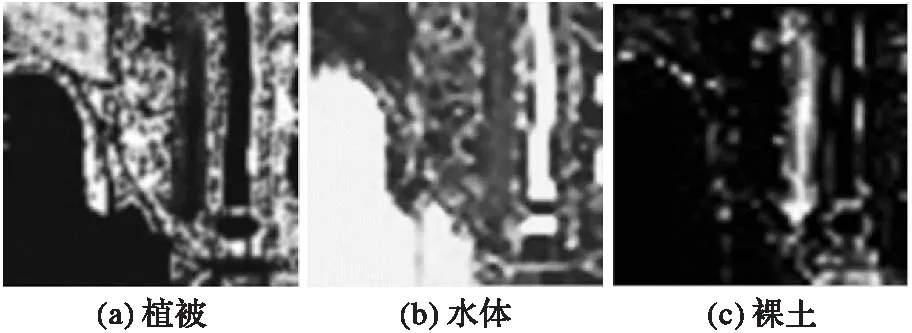
图4 MRF-NMF的丰度分解结果Fig. 4 Decomposition results of abundances with MRF-NMF

表1和表2分别列出了四种算法的端元光谱和丰度分布分解结果的精度分析。其中，利用光谱角距离(Spectral Angle Distance, SAD)计算端元光谱估计精度，利用均方根误差(Root Mean Square Error, RMSE)计算端元丰度估计精度。

SAD的计算公式为：

(11)

整幅图像的RMSE为：

(12)

从表1～2可以看出，无论是端元光谱，还是端元丰度，MRF-NMF在四种算法中的分解精度都最高。其中，MRF-NMF的端元光谱分解精度相比MVC-NMF提高了10.6%，比PSNMFSC提高了12.3%，比APS-NMF提高了14.1%；MRF-NMF的端元丰度分解精度相比MVC-NMF提高了14.4%，比PSNMFSC提高了15.9%，比APS-NMF提高了15.3%。

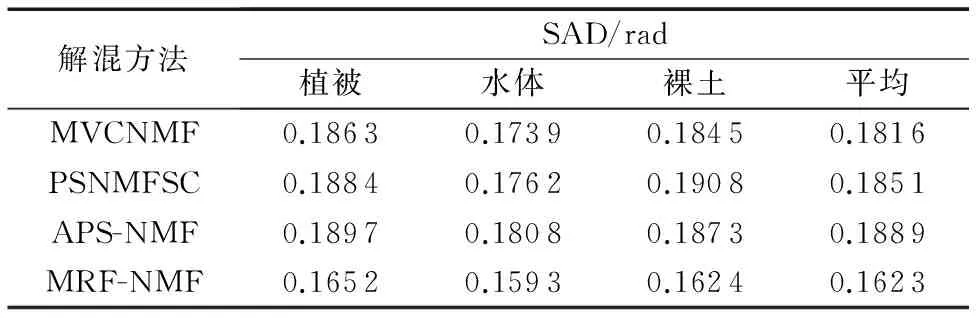
表1 端元光谱分解结果精度Tab. 1 Precision of decomposition results of endmembers’ spectrum

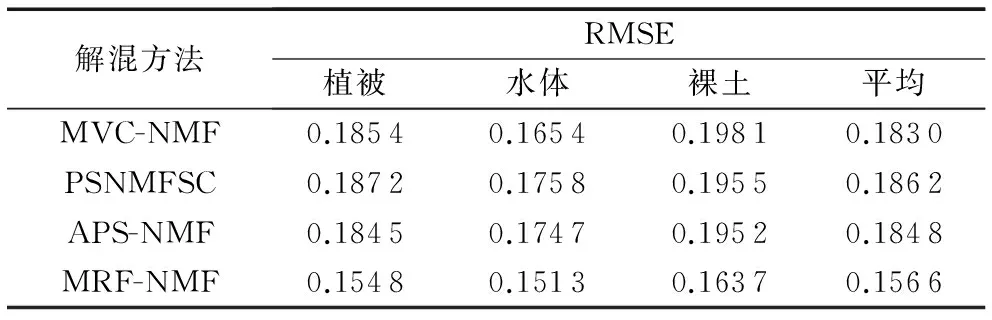
表2 丰度分布估计结果精度Tab. 2 Precision of estimation results of abundance distribution

2.2 真实数据实验2

实验数据1的自然场景以成片分布的水、植被和裸土等自然场景为主，空间相关特征显著。为比较和验证算法对空间相关程度不同的场景的解混效果，选择获取于1995年7月美国Nevada州Cuprite采矿区的机载可见光/红外成像光谱仪(Airborne Visible InfRared Imaging Spectrometer, AVIRIS)高光谱数据作为实验数据2，如图5所示。实验数据2的全局Moran’I指数为0.224 7，相对于实验数据1，其空间相关程度明显降低，说明矿区内各种矿物的分布较为分散和杂乱。

图5 Cuprite矿区AVIRIS高光谱数据Fig. 5 AVIRIS hyperspectral data of Cuprite mining field

图5中的A、B、C、K、M等字样分别代表该地区5种广泛分布的矿物Alunite、Buddingtointe、Calcite、Kaolinite和Muscovite的大致分布位置。

该图像大小为400列、350行，空间分辨率为20 m，波长范围为1.99～2.48 μm ，光谱分辨率为10 nm，共50波段，依次为AVIRIS原始谱段中的第172～221波段。该地区位于美国Nevada州南部，地表多为裸露矿物，基本无植被覆盖。相对于真实数据实验1中的美国华盛顿特区HYDICE高光谱数据，该数据的空间相关特征不明显，几种主要矿物空间分布的随机性较大。

由于AVIRIS为机载光谱成像仪，空间分辨率(20 m)相对较高，可合理假设图像中每种端元都含有一定数量的纯像元。因此，本文通过在原图像中人工选择参考点的方式，收集每种端元(地物)的光谱作为参考值，利用全约束最小二乘法计算端元的丰度参考值。

下面重复实验数据1的实验环节，以此对比和验证算法针对不同场景时的性能表现。需要说明的是，实验只针对上述五种主要矿物类型进行解混实验，对于其余小目标对应的地物类型的处理与实验数据1完全相同，具体情况不再赘述。

图6为本文算法MRF-NMF对应的Cuprite采矿区AVIRIS数据丰度估计结果。由于篇幅限制，其他参考算法的结果图不再一一列出。

将图6中每种地物的MRF-NMF丰度估计值与前文中利用全约束最小二乘法计算出的丰度参考值进行比较，相似度均在85%以上，说明MRF-NMF算法能够有效分离出五种不同地物类型及其大体分布位置。

图6 Cuprite矿区AVIRIS高光谱数据MRF-NMF丰度估计结果Fig. 6 Abundance estimation results of AVIRIS hyperspectral data of Cuprite mining field with MRF-NMF

表3～4分别给出了四种解混算法的端元光谱和丰度解混的精度分析结果。

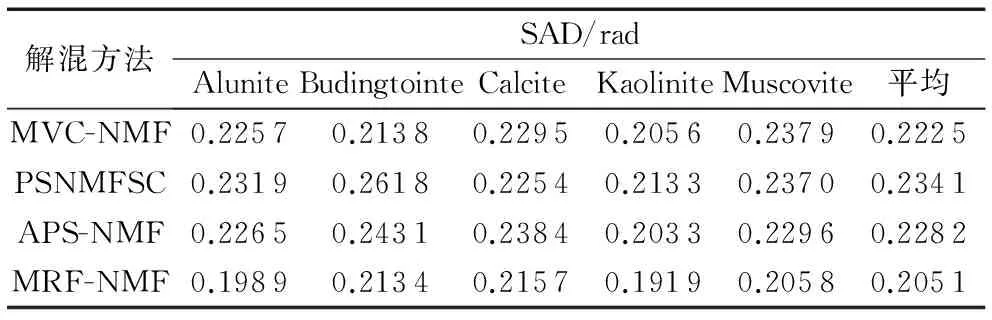
表3 Cuprite采矿区数据的端元光谱分解结果精度Tab. 3 Precision of endmembers’ spectrum decomposition results of Cuprite mining field

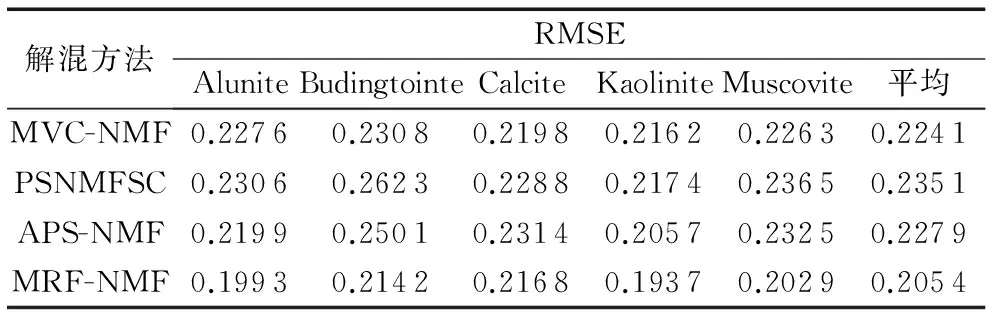
表4 Cuprite采矿区数据的丰度分布估计结果精度Tab. 4 Precision of abundance distribution estimation results of Cuprite mining field

从表3～4中可以看出，四种解混算法均能有效分解出五种主要矿物类型，本文提出的MRF-NMF算法性能最好。以端元光谱分解结果为准，MRF-NMF比MVC-NMF、PSNMFSC和APS-NMF三种算法的分解精度分别提高了7.82%、12.4%和10.1%；以丰度估计结果为准，MRF-NMF比MVC-NMF、PSNMFSC和APS-NMF三种算法的分解精度分别提高了8.34%、12.6%和9.87%。

上述结果表明，MRF-NMF在实验数据空间相关程度显著减小的情况下，相对于其他三种NMF代表性算法，仍具有较为明显的精度优势，只是比实验数据空间相关程度显著时略有下降。

最后，为了更全面地分析算法解混性能，给出了上述四种算法在Matlab 7.0环境下分别解混上述两组空间相关程度不同的实验数据时运行时间的统计与比较结果，如表5所示。其中，为便于和Cuprite矿区数据进行比较，截取了美国华盛顿特区HYDICE数据中相同行列数(400列、350行)的子区作为实验数据；波段数也都统一选定为50(从美国华盛顿特区HYDICE数据中随机选取50个波段)，同时将两组实验数据的感兴趣端元数量均设定为5(HYDICE数据中增加屋顶、道路等两类小面积感兴趣地物)。

从表5中可以看出，本文算法MRF-NMF的运行时间要明显少于其他三种算法，运算效率最高；同时该算法在处理空间相关程度较低的数据时耗时有所增加。分析其原因，主要是由于空间相关程度的降低使得本文算法迭代次数增多。

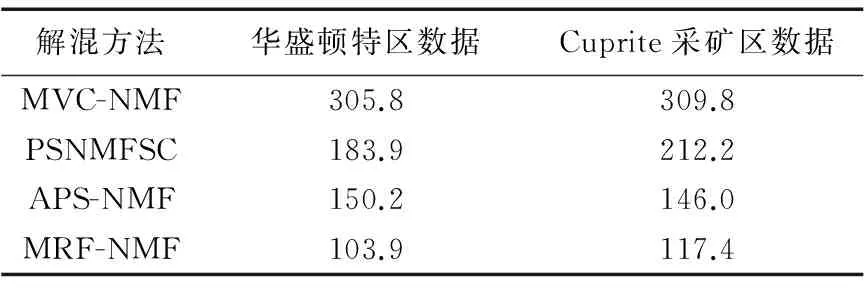
表5 空间相关程度不同时不同算法运行时间比较 sTab. 5 Running time comparison of different algorithms with different spatial correlation s

3 结语

本文针对大多数NMF扩展方法中容易忽略的端元分布空间相关特征，利用MRF模型对其进行描述，提出了一种新的基于NMF的高光谱解混方法。该方法通过构建端元空间分布的能量函数来表征空间相关特征，作为与标准NMF目标函数相互独立的辅助函数，舍弃了构造NMF目标函数内部约束项的传统做法，为基于NMF的高光谱解混研究提供了新的思路。

实验结果表明，对于大部分真实高光谱数据，所提方法的分解精度和计算效率均优于其他几种代表性对比算法。

尽管空间相关特征在高光谱图像中普遍存在，但并非全部真实数据都同时具有显著的(相邻像元)空间相关特征。实验结果也表明了当空间相关程度不高时，本文算法性能会出现小幅下降。可以预见，如果出现实验图像的像元之间空间相关程度接近于零或负相关等极端情况，算法性能可能会出现较为严重的退化。如何进一步稳定算法性能，将是下一步研究工作的主要内容。

References)

[1] LEE D D, SEUNG H S. Learning the parts of objects by non-negative matrix factorization [J]. Nature, 1999, 401: 788-791.

[2] PAUCA V P, PIPER J, PLEMMONS R J. Nonnegative matrix factorization for spectral data analysis [J]. Linear Algebra and its Applications, 2006, 416(1): 29-47.

[3] MIAO L D, QI H R. Endmember extraction from highly mixed data using minimum volume constrained nonnegative matrix factorization [J]. IEEE Transactions on Geoscience and Remote Sensing, 2007, 45(3): 765-777.

[4] ZYMNIS A, KIM S J, SKAF J, et al. Hyperspectral image unmixing via alternating projected subgradients [C]// ACSSC 2007: Proceedings of the 2007 Conference Record of the Forty-First Asilomar Conference on Signals, Systems & Computers. Piscataway, NJ: IEEE, 2007: 1164-1168.

[5] JIA S, QIAN Y T. Constrained nonnegative matrix factorization for hyperspectral unmixing [J]. IEEE Transactions on Geoscience and Remote Sensing, 2009, 47(l): 161-173.

[6] 杜世强,石玉清,王维兰,等.基于图正则化的半监督非负矩阵分解[J].计算机工程与应用,2012,48(36):194-200.(DU S Q, SHI Y Q, WANG W L, et al. Graph regularized-based semi-supervised non-negative matrix factorization [J]. Computer Engineering and Applications, 2012, 48(36): 194-200.)

[7] 刘建军,吴泽彬,韦志辉,等.基于空间相关性约束稀疏表示的高光谱图像分类[J].电子与信息学报,2012,34(11):2666-2671.(LIU J J, WU Z B, WEI Z H, et al. Spatial correlation constrained sparse representation for hyperspectral image classification [J]. Journal of Electronics & Information Technology, 2012, 34(11): 2666-2671.)

[8] CHEN B L, LI M, WANG J X, et al. Disease gene identification by using graph kernels and Markov random fields [J]. Science China Life Sciences, 2014, 57(11): 1054-1063.

[9] 姜小燕,孙福明,李豪杰.基于图正则化和稀疏约束的半监督非负矩阵分解[J].计算机科学,2016,43(7):77-82.(JIANG X Y, SUN F M, LI H J. Semi-supervised nonnegative matrix factorization based on graph regularization and sparseness constraints [J]. Computer Science, 2016, 43(7): 77-82.)

[10] DOBRUSHIN P L. The description of a random field by means of conditional probabilities and conditions of its regularity [J]. Theory of Probability and its Applications, 1968, 13 (2): 197-224.

[11] SPITZER F. Markov random fields and gibbs ensembles [J]. American Mathematical Monthly, 1971, 78 (2): 142-154.

[12] DENG H W, CLAUSI D A. Unsupervised image segmentation using a simple MRF model with a new implementation scheme [J]. Pattern Recognition, 2004, 37(12): 2323-2335.

[13] BIOUCAS-DIAS J M, NASCIMENTO J M P. Hyperspectral subspace identification [J]. IEEE Transactions on Geoscience and Remote Sensing, 2008, 46(8): 2435-2445.

[14] 袁博.高光谱像元解混盲处理方法研究——面向盲分解的相关性分析与应用[D].北京:中国科学院大学,2015:45-48.(YUAN B. Research on blind processing algorithms of hyperspectral unmixing — correlation analysis and application of blind decoposition [D]. Beijing: University of Chinese Academy of Sciences, 2015: 45-48.)

[15] LEE D D, SEUNG H S. Algorithms for nonnegative matrix factorization [J]. Advances in Neural Information Processing Systems, 2001, 13(6): 556-562.

[16] 吴金彪.D-N交替迭代法及其收敛性分析[J].数值计算与计算机应用,2002,23(2):121-130.(WU J B. D-N commutative method and its convergence [J]. Journal on Numerical Methods and Computer Applications, 2002, 23(2): 121-130.)

[17] 朱子明,祁新华.基于Moran’I的闽南三角洲空间发展研究[J].经济地理,2009,29(12):1977-1980.(ZHU Z M, QI X H. Research on spatial development of minnan delta basing on Moran’I [J]. Economic Geography, 2009, 29(12): 1977-1980.)

YUANBo, born in 1982, Ph. D., lecturer. His research interests include hyperspectral data processing, Internet of things engineering.

ApplicationofMRF’sspatialcorrelationmodelinNMF-basedlinearunmixing

YUAN Bo*

(CollegeofComputerandInformationEngineering,NanyangInstituteofTechnology,NanyangHenan473004,China)

Aiming at the problems of initialization and “local minima” of Non-negative Matrix Factorization (NMF) in hyperspectral unmixing, a spatial correlation constrained NMF linear unmixing algorithm based on Markov Random Field (MRF) (MRF-NMF) was proposed. Firstly, the number of endmembers was estimated by Hyperspectral Signal identification by minimum error (HySime) method, the endmember matrix and abundance matrix were initialized by Vertex Component Analysis (VCA) and Fully Constrained Least Squares (FCLS). Secondly, the energy function of depicting the spatial distribution characteristics of ground objects was established by using MRF to depict the spatial correlation distribution features of ground objects. Finally, the spatial correlation constraint function based on MRF and the NMF standard objective function were used for unmixing in the form of alternating iteration, and the endmember information and abundance decomposition results of hyperspectral data were obtained. The theoretical analysis and experimental results of real data show that, with hyperspectral data of low spatial correlation, compared with the three reference algorithms of Minimum Volume Constrained NMF(MVC-NMF), Piecewise Smoothness NMF with Sparseness Constraints (PSNMFSC) and NMF with Alternating Projected Subgradients (APS-NMF), the endmember decomposition precision of MRF-NMF increases by 7.82%, 12.4% and 10.1%, and the abundance decomposition precision of MRF-NMF increases by 8.34%, 12.6% and 9.87%. The proposed MRF-NMF can make up for NMF’s deficiency in depicting spatial correlation features, and reduce the spatial energy distribution error of ground objects.

Non-negative Matrix Factorization (NMF); hyperspectral linear unmixing; spatial correlation; Markov Random Field (MRF); alternative iteration; spatial energy

2017- 06- 12;

2017- 08- 29。

袁博(1982—)，男，河南南阳人，讲师，博士，主要研究方向：高光谱数据处理、物联网工程。

1001- 9081(2017)12- 3563- 06

10.11772/j.issn.1001- 9081.2017.12.3563

(*通信作者电子邮箱nylgyb@163.com)

TP751.1

A