外辐射源雷达滑窗扩展相消算法并行实现

2018-01-08

雷达科学与技术 2017年2期

(武汉大学电子信息学院,湖北武汉430072)

外辐射源雷达滑窗扩展相消算法并行实现

张坚,万显荣,刘玉琪

(武汉大学电子信息学院,湖北武汉430072)

杂波抑制是外辐射源雷达信号处理中的关键技术之一。ECA-S算法突破了ECA-B算法在实际数据处理中对分段数的限制,通过给每段分段信号增添滑窗,在增加分段数的同时保证了足够的积累时间,具有更好的滤波效果,但这一改进效果是以增大空间和时间复杂度为代价而得到。结合图形处理器(GPU)数据吞吐量大、并行处理简单、适宜解决计算密集型问题的特点,提出一种适用于GPU处理的ECAS时域杂波抑制并行实现方法。实测数据验证了该算法的有效性,并满足实时处理的需求。

外辐射源雷达;时域杂波抑制;滑窗扩展相消算法(ECA-S);并行实现

0 引言

近年来,外辐射源雷达[1-4]由于其巨大的潜在价值,在军用和民用方面均引起了广泛关注。它利用环境中已存在的照射源进行目标探测,具有绿色环保、操作隐蔽的特点。

在外辐射源雷达中,监测通道中不仅含有目标的回波信息,同时还存在直达波和多径杂波,后者的强度远远强于目标回波,经相干积累后杂波仍具有很高的距离副瓣和多普勒副瓣,使得距离多普勒谱的基底抬高,导致目标被湮没在回波谱中。因此,杂波抑制是外辐射源雷达信号处理中的关键技术之一。利用只含有直达波和多径信息的参考信号,可以从监测信号中移除杂波信息。文献[5-10]给出了杂波抑制的不同实现方法,它们各自具有不同的计算复杂度和处理效果。

在这些方法中,广泛使用到的就是扩展相消算法(Extensive Cancellation Algorithm,ECA)和它的分段版本——分段扩展相消算法[6](Extensive Cancellation Algorithm Batches,ECA-B)。ECA算法利用参考信号构建杂波子空间矩阵,通过消去监测信号在杂波空间的投影分量来实现杂波抑制。ECA算法要求在整个积累时间内计算自适应滤波系数,这使得算法构建的杂波空间矩阵较大,最终导致算法的计算量和运算存储空间很大。相对地,ECA-B算法将监测信号和参考信号分成多段,分别计算每一段的自适应滤波系数,最终滤波结果即为每一段计算结果的组合。ECA-B算法在计算量相当的情况下,降低杂波子空间的维度和最大运算储存空间消耗,增加了零陷宽度。并且通过分段处理,加快了自适应滤波系数的更新速率,算法在非平稳环境下具有更好的鲁棒性。但是算法的零陷展宽由每段数据的ECA算法零陷决定,每段数据的积累时间不能过少,即ECA-B算法的最大分段数较少,制约了算法并行化实现,不利于实时处理。为了保持ECA-B运算存储空间消耗较小以及在非平稳环境下鲁棒性强的优点,并消除分段带来的影响,ECA-S[11]算法被提出。算法采用ECA-B算法的分段思想及相似的算法流程,但是在估计杂波子空间系数时,在参考信号和监测信号两端分别各取一段滑窗信号,用滑窗后参考信号构建的杂波子空间和对应的监测信号来估计杂波子空间系数。算法在参数估计时需要作滑窗处理,使得整体运算量大大增加。

CUDA适合解决计算密集型问题,为基于GPU的ECA-S算法并行实现提供了条件。

目前,已有一些研究人员在GPU平台上并行实现外辐射源雷达信号处理算法,并取得了较好的加速效果。文献[12-14]使用CUDA对外辐射源雷达杂波抑制算法进行并行处理。同时,基于GPU并行算法实现也被用于其他科学计算领域[15-18]。

1 算法描述

1.1 ECA和ECA-B算法

假设照射源发射信号为s(t),则外辐射源雷达参考通道和监测通道接收到的回波信号可分别表示为sref(t)和ssurv(t):

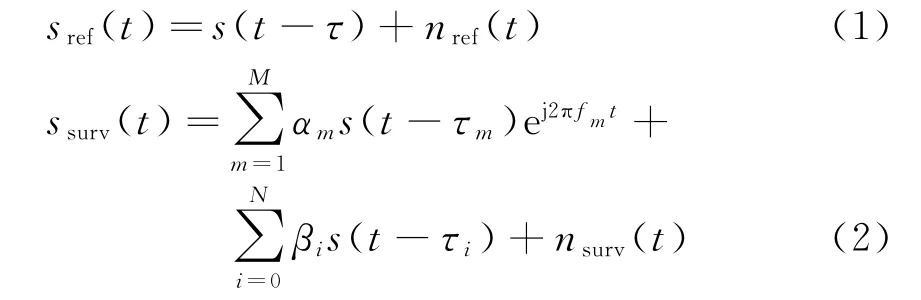
式中,τ为参考通道回波相对发射信号的延时,βi,τi分别为N条多径中第i条回波衰减和时延,其中i=0时为该多径为直达波的情况,αm,τm,f m分别为M个目标中第m个目标的衰减、时延和多普勒频移,nref(t),nsurv(t)分别为参考通道和监测通道中的噪声,一般可认为是高斯白噪声。

利用最小二乘算法(Least Square,LS)进行相消滤波,即求下式的最小残留信号能量:

容易求得

可得ECA算法杂波抑制后的信号为

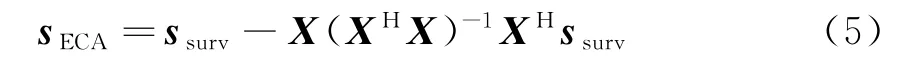
ECA-B算法将参考和监测信号等分为B段,每一段长度为n L的信号分别进行ECA滤波,可得到第i段自适应滤波权矢量为

滤波后的信号表示为

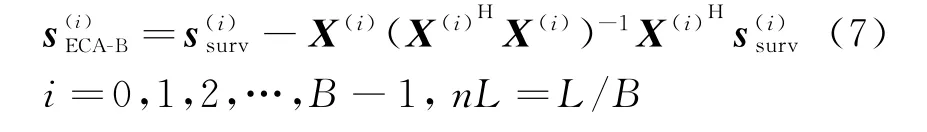
信号总积累时间为T,则每段ECA滤波的积累时间T B=T/B。对于T B的选取,有两方面的考虑:一方面希望T B尽量长以获得更小的多普勒分辨率和减少自适应损失;另一方面又希望T B尽量短从而使算法更加具有鲁棒性,更能应对环境变量快速变化的情况。这些考虑使得分段数B的选取受到限制,两方面的要求都不能得到较好的满足。

1.2 ECA-S算法

为了克服上述的限制,ECA-S算法通过引入滑窗信号来使得两方面的要求不再对立:每段信号加上滑窗信号使得足够长的积累时间用于自适应估计;增大分段数使得自适应系数的更新速率足够快以适应复杂的环境情况。这样可以满足在分段数足够大的同时保障每段信号的积累时间充分长的需求。

假设ECA-S算法将参考信号和监测信号分为B段,每一段参考信号和监测信号都向前和向后多取Ns/2个点作为滑窗。则第i段信号滤波后为

图1为ECA-S算法的流程图。对第i段信号,首先利用加入滑窗后的求得自适应权矢量α(i),然后利用构建杂波空间矩阵X(i),最后依据式(8)计算得到滤波处理结果

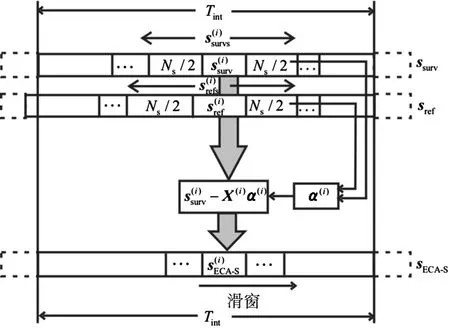
图1 ECA-S算法处理流程

2 算法的改进和并行实现

2.1 R x的改进计算

考虑到矩阵X(i)和的特殊结构,矩阵中元素与参考信号的对应关系为

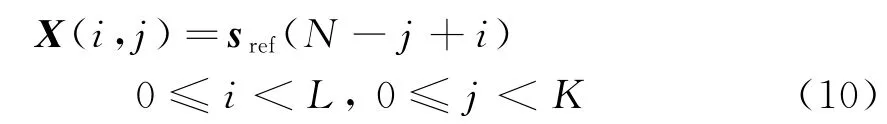
式中,X(i,j)表示矩阵X中第i行第j列的元素。

容易得到矩阵X的共轭转置矩阵XH为

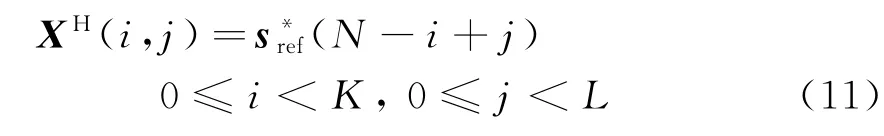
式中,∗表示取共轭。

则有

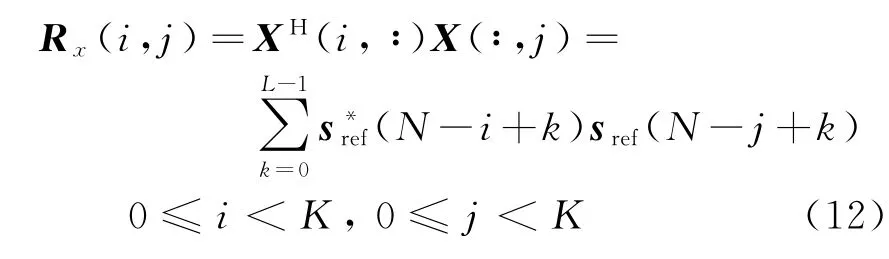
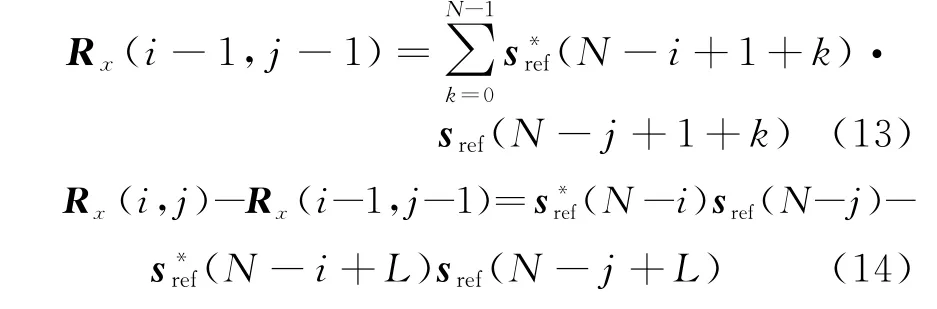
由式(14)可知,关于R x(i,j)的计算有极大的计算冗余,直接计算需要L次复数浮点乘法和L-1次复数加法,而若利用对角元素的前一计算值R x(i-1,j-1),则只需要两次复数乘法和两次复数加法即可得到。从而可以通过计算矩阵第1行的值,然后迭代计算剩余K-1行的值,并最终得到R x,显然此算法可以极大降低计算量。对比直接矩阵相乘,两种方法计算量之比近似为K。改进方法从原理上大大减少了计算量[12]。

在ECA及其改进算法的滤波过程中,都可通过式(10)和式(11)从参考信号得到对应杂波空间矩阵X中各元素的值,从而不需要直接构建X,节省了存储空间。特别是在ECA-S算法中,免去了构建的空间,两者都可从参考信号中提取出各元素的值。

2.2 分段ECA-S滤波并行计算

在使用CPU进行ECA-S滤波时,每一段数据都是循环读取且依次进行处理的。这是一个串行处理的过程,总处理时间是各段数据处理时间之和。而在CUDA对数据进行并行实现中,可以将各段数据一起读取同时进行处理,这样总处理时间只是各段处理时间中最长的部分,理论上加速比近似为B。实际处理过程中由于GPU对于双精度浮点数据的处理能力较弱,数据的传输速率也慢于CPU,同时由于GPU的内核数有限,最大可并行度受不同显卡内核的限制,无法做到B段数据全部并行一起处理,使得加速比有所降低。这些硬件上的阻碍可通过更换更先进的设备来优化。

在CUDA编程模型中,CPU作为主机端,只负责数据的传递分配、运行参数的配置等,而将大规模的数据计算交给GPU设备端进行处理。GPU按照粒度粗细分为Grid,Block和Thread,Grid内部Block间粗粒度并行,数据间无法直接通信,Block内部Thread间细粒度并行,通过__syncthread()函数保证数据同步。在实际编程实现过程中,将每一步计算中可以并行计算的部分写成一个或多个核函数,CPU控制整体的计算流程,GPU运行Kernel函数并行计算实现。

2.3 程序流程

程序整体实现流程如图2所示。首先读取数据,将参考和监测通道的数据拷贝到设备端。可以将block Dim.y设置为分段数B,第i段信号可以通过blockIdx.y来分别读取。依据与第i段参考信号中数据的一一对应关系,可以免去构建杂波矩阵,节省了存储空间。由于构建X(i)和的参考信号都是从原始参考信号相同的位置截取的一段,不同的是前者比后者多截取了长度为Ns的滑窗信号,为计算方便,可以将滑窗信号的选取方式改为只在分段信号后截取,这样可以用相同的指针表示两者首元素的位置。实际处理结果表明这种滑窗选取方式对滤波效果无影响。的求逆采用了文献[18]介绍的Gauss-Jordan原地求逆算法,相比基础的Gauss-Jordan顺序消去法,节省了一半的显存空间和计算量。由于GPU的硬件结构限制,Thread的最大数目不能超过规定数值,所以在计算矩阵相乘时,一个Block计算一个元素,若需要累加的项数超过限制,则每个Kernel计算多个相乘的结果并累加,最后对Block内所有线程进行规约求和。同时由于的计算使用的是改进方法,整个计算过程中的矩阵相乘部分都是矩阵乘上列向量,结果仍为列向量。可将block Dim.x设为列向量的行数,Grid内的x维用来计算相乘结果。

每一段监测信号杂波抑制后的计算结果保存在sECA-S的对应位置,所有线程计算完后即可得到ECA-S算法的结果。

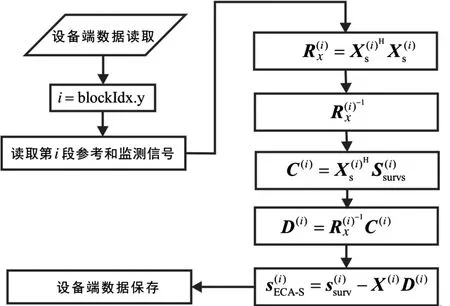
图2 程序流程图

3 实测数据处理结果

2013年11月,武汉大学外辐射源雷达实验基地利用FM广播信号进行了目标探测的外场实验。信号处理的软硬件配置如表1所示。图3为选取其中一段FM信号绘制的杂波抑制前的距离多普勒谱,其中信号中心频率为103.8 MHz,带宽为500 k Hz。采用ECA-S算法进行并行计算,抑制距离元数为500,滑窗信号长度取50 000,监测通道数据总长度为500 000,采用双精度浮点计算,分段数为100时,总耗时为0.861 s,相同设备下串行处理平均时间为18.531 s,总体加速比为21.5。图4为ECA-S杂波抑制前后距离多普勒谱,杂波抑制前目标被直达波和多径杂波旁瓣掩盖,杂波抑制后目标凸显。同时对相同的数据使用ECA-B算法滤波处理,分段数取10,图5为ECA-B滤波后的距离多普勒图。对比可以看到,图5中的3个目标都能在图4中找到对应,然而后者比前者多观测到一个低速目标。该实验现象验证了ECA-S算法相比ECA-B算法对低速目标具有更好的观测效果。图6为ECA-S算法使用Matlab和GPU计算所得结果的绝对误差,10-5量级的误差完全可以忽略不计。

表1 软硬件配置情况

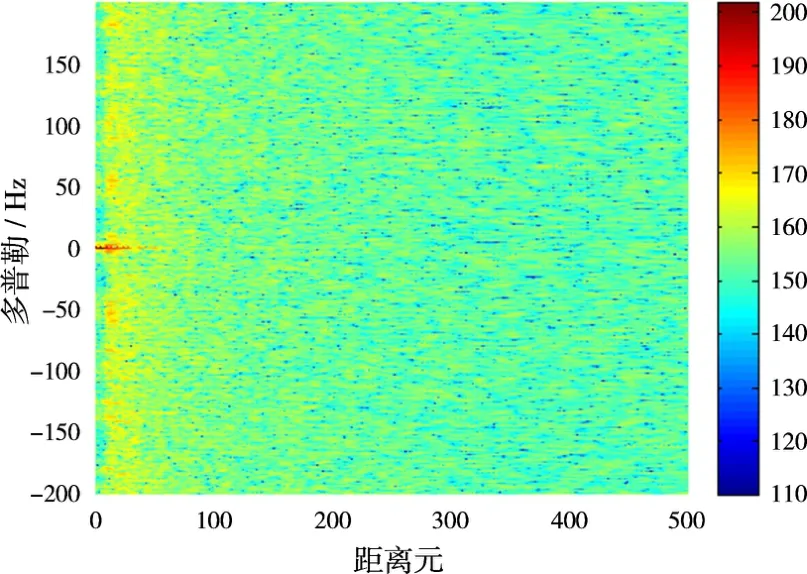
图3 杂波抑制前的距离多普勒谱

图4 ECA-S抑制后的距离多普勒图

图5 ECA-B抑制后的距离多普勒图

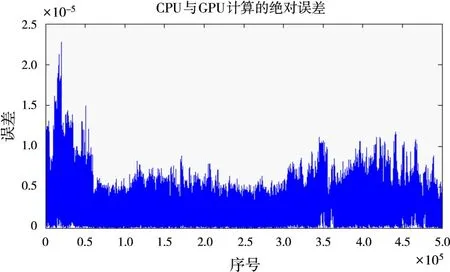
图6 GPU与Matlab计算的绝对误差

为了探究ECA-S算法处理时间与分段数的关系,选取不同的分段数,分别使用C语言和CUDA进行数据处理,处理时间如图7所示。可以看出,随着分段数的增加,串行处理时间线性增长,而CUDA处理时间基本不变,对应的加速比也随之线性增加。这是由于滑窗信号的长度相对分段信号较长,分段信号长度变化对整体影响不大,从而每段信号的滤波处理时间基本不变,串行处理时间随着分段数的变化而线性增加,而在GPU的最大并行处理限度内,并行处理时间不变。

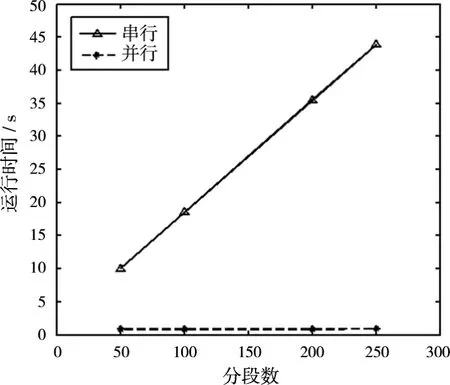
图7 不同分段数下ECA-S算法处理时间

4 结束语

本文针对ECA-S算法处理时间过长而不利于实时化的问题,使用CUDA在GPU上对算法进行并行加速实现。实测数据验证了该算法的有效性。相对于常规方法,该方法能极大减少显存需求,缩短计算时间,使得ECA-S算法能够满足外辐射源雷达杂波抑制的实时处理要求。

[1]万显荣.基于低频段数字广播电视信号的外辐射源雷达发展现状与趋势[J].雷达学报,2012,1(2):109-123.

[2]KUSCHEL H,O’HAGAN D.Passive Radar from History to Future[C]∥11th International Radar Symposium,Vilnius,Lithuania:IEEE,2010:1-4.

[3]HOWLAND P E,GRIFFITHS H D,BAKER C J.Passive Bistatic Radar Systems[M]∥Cherniakov M.Bistatic Radar:Emerging Technology.Weinheim:Wiley,2008:247-311.

[4]HOWLAND P E,MAKSIMIUK D,REITSMA G.FM Radio Based Bistatic Radar[J].IEE Proceedings:Radar,Sonar and Navigation,2005,152(3):107-115.

[5]CARDINALI R,COLONE F,FERRETTI C,et al.Comparison of Clutter and Multipath Cancellation Techniques for Passive Radar[C]∥IEEE Radar Conference,Boston,MA:IEEE,2007:469-474.

[6]COLONE F,O’HAGAN D W,LOMBARDO P,et al.A Multistage Processing Algorithm for Disturbance Removal and Target Detection in Passive Bistatic Radar[J].IEEE Trans on Aerospace and Electronic Systems,2009,45(2):698-722.

[7]PALMER J E,SEARLE S J.Evaluation of Adaptive Filter Algorithms for Clutter Cancellation in Passive Bistatic Radar[C]∥IEEE Radar Conference,Atlanta,GA:IEEE,2012:493-498.

[8]MELLER M,TUJAKA S.Processing of Noise Radar Waveforms Using Block Least Mean Squares Algorithm[J].IEEE Trans on Aerospace and Electronic Systems,2012,48(1):749-761.

[9]ZHAO Y D,ZHAO Y K,LU X D,et al.Block NLMS Cancellation Algorithm and Its Real-Time Implementation for Passive Radar[C]∥IET International Radar Conference,Xi’an:IET,2013:1-5.

[10]GUAN X,HU D H,ZHONG L H,et al.Strong Echo Cancellation Based on Adaptive Block Notch Filter in Passive Radar[J].IEEE Geoscience and Remote Sensing Letters,2015,12(2):339-343.

[11]COLONE F,PALMARINI C,MARTELLI T.Sliding Extensive Cancellation Algorithm for Disturbance Removal in Passive Radar[J].IEEE Trans on Aerospace and Electronic Systems,2016,52(3):1309-1326.

[12]陈伟,万显荣,张勋,等.外辐射源雷达多通道时域杂波抑制算法并行实现[J].雷达学报,2014,3(6):686-693.

[13]武勇,王俊,张培川,等.CUDA架构下外辐射源雷达杂波抑制并行算法[J].西安电子科技大学学报,2015,42(1):104-111.

[14]李晓波,关欣,仲利华,等.基于GPU的外辐射源雷达信号处理实时实现方法[J].系统工程与电子技术,2014,36(11):2192-2198.

[15]邓婕,张兴浦,陈世友.基于GPU的信息融合并行方法研究[J].舰船电子工程,2016,36(6):35-37.

[16]沈聪,高火涛.使用GPU加速计算矩阵的Cholesky分解[J].计算机应用与软件,2016,33(9):284-287,305.

[17]贾春刚,郭立新,刘伟.基于GPU的并行FDTD方法在二维粗糙面散射中的应用[J].电波科学学报,2016,31(4):683-687.

[18]刘丽,沈杰,李洪林.基于GPU的矩阵求逆性能测试和分析[J].华东理工大学学报(自然科学版),2010,36(6):812-817.

Parallel Implementation of Sliding Extensive Cancellation Algorithm for Passive Radar System

ZHANG Jian,WAN Xianrong,LIU Yuqi
(School of Electronic Information,Wuhan University,Wuhan430072,China)

Cancellation of clutter is one of the key signal processing techniques in passive radar.Sliding extensive cancellation algorithm(ECA-S)has broken through the limitations of extensive cancellation algorithm batches(ECA-B)in the number of batches during real data processing.By adding a sliding window to each segmented signal,a sufficient integrated time is ensured while the number of batches is increased,and a batter filtering effect is obtained.However,this improvement is achieved at the cost of increasing the space and time complexity.Considering the advantages of graphic processing unit(GPU)in high memory throughput,parallel processing,and computationally intensive problem,this paper proposes a parallel realization of ECA-S algorithm based on GPUs.The experimental results verify the effectiveness of the proposed algorithm.It also meets the demands of real-time processing.

passive radar;time-domain clutter suppression;sliding extensive cancellation algorithm(ECA-S);parallel implementation

TN958.97

1672-2337(2017)02-0115-05

10.3969/j.issn.1672-2337.2017.02.001

2016-11-02;

2016-12-02

国家重点研发计划(No.2016YFB0502403);国家自然科学基金(No.61331012,61371197,U1333106,61271400);湖北省科技支撑项目(No.2015BCE075)