低轨卫星增强BDS卫星定轨技术探讨

王 乐，燕兴元，张 勤，黄观文，秦志伟

(长安大学 地质工程与测绘学院，西安 710000)

低轨卫星增强BDS卫星定轨技术探讨

王 乐，燕兴元，张 勤，黄观文，秦志伟

(长安大学 地质工程与测绘学院，西安 710000)

针对BDS的GEO卫星与地面监测站的几何构型变化缓慢，导致其站星几何结构较差、定轨精度较低，以及中国区域地面监测站难以对BDS IGSO和MEO卫星形成连续多重覆盖观测，导致有效观测弧段较短、相对于基于全球地面监测站的定轨精度低、影响BDS广播星历的服务性能等问题，探讨一种将载有星载GNSS接收机的低轨卫星作为BDS卫星精密定轨的高动态监测站，联合BDS地面监测站数据，同时解算BDS卫星轨道和钟差以及低轨卫星轨道等参数的技术。实验结果证明该技术可极大改善测站与卫星的空间几何构型，增加有效观测弧长，实现多重覆盖观测，进而提高BDS 3种类型卫星轨道的确定精度，提升BDS的服务性能。

北斗系统；低轨卫星；地面监测站；精密定轨；广播星历

0 引言

北斗卫星导航系统(BeiDou navigation satellite system，BDS)是我国自主开发、独立运行的全球卫星导航系统(global navigation satellite system，GNSS)，可为全球或区域不同需求的用户提供定位导航授时(positioning navigation timing，PNT)服务，应用广泛。北斗区域卫星导航系统于2012-12-27开始正式向亚太区域提供服务，包括5颗地球静止轨道(geostationary Earth orbit，GEO)卫星，5颗地球倾斜同步轨道(inclined geosynchronous satellite orbit，IGSO)卫星和4颗中圆地球轨道(medium Earth orbit，MEO)卫星[1]。BDS拟将在2020年实现全球组网，建设成为包括5颗GEO卫星和30颗非静止轨道卫星的全球卫星导航系统[2]。作为空间基准，BDS卫星轨道的精度直接影响用户的定位性能，是衡量BDS系统服务性能的主要指标[3-4]。

BDS为异构星座，包含GEO、IGSO和MEO 3种类型轨道。GEO相对地面基本静止，其“静地”性导致GEO卫星和地面监测站之间的几何构型基本保持不变，从而导致GEO轨道切向分量解算精度差。目前，GNSS卫星精密定轨主要依赖于全球均匀分布的地面监测站收集的观测数据。受限于政治因素和国土面积，BDS难以形成全球均匀分布的地面运控监测站网络。可控的BDS一级和二级地面运控监测站全部分布在中国境内，形成中国区域地面监测网，难以对IGSO/MEO卫星形成连续多重覆盖观测，致使BDS IGSO/MEO定轨精度偏低。所以必须改进和增加BDS可控站的站址资源以提高BDS卫星轨道解算精度。

星载GNSS技术是20世纪90年代迅速发展起来的一种新的低地球轨道(low Earth orbit，LEO)卫星精密定轨技术，具有成本低、设备轻便、全天候、高精度、连续观测的优点，目前已经成为低轨卫星的主要测定轨手段[5]。星载GNSS技术利用GNSS卫星精密轨道钟差和LEO GNSS观测数据对低轨卫星进行精密轨道解算。如果已知低轨卫星精密轨道，则低轨卫星星载接收机可作为高动态的天基监测站参与GNSS卫星精密定轨。

本文重点探讨将低轨卫星作为可控的高动态天基监测站，联合地面监测站网络，综合测定BDS卫星轨道的技术。

1 基于地面监测站的BDS卫星精密定轨技术进展

卫星精密定轨方法主要包括动力学法、几何法和简化动力学法。动力学法首先将后续时刻的卫星状态参数归算到初始位置，然后由观测值确定初始时刻的卫星状态，最后根据动力学方程积分得到任意时刻的运动状态矢量[6-7]。几何法以观测到的4颗以上卫星距离观测量为基础，通过空间距离后方交汇获取卫星的瞬时坐标[8]。简化动力学法在动力学模型信息和几何观测信息间进行最优加权，从而合理平衡观测信息和动力学信息以提高精密定轨精度[9]。

运动方程的数学模型可用卫星初始轨道参数描述为

a=F(r，v，p，t)。

(1)

式中：a为卫星的摄动加速度；F为摄动函数；r为卫星的位置矢量；v为卫星的速度矢量；p为动力学参数矢量；t为时间。

地面监测站观测方程的数学模型描述为

Lsta=Fsta(Xgns，Xsta，Xoth，t)+εsta。

(2)

式中：Lsta为地面监测站的观测数据；Fsta为测站观测函数；Xgns、Xsta和Xoth分别为GNSS卫星轨道参数、地面监测站相关参数和其他待估参数；t为时间；εsta为测站观测噪声。

针对全球定位系统(global positioning system，GPS)卫星定轨理论的研究趋于成熟，可供BDS借鉴，此处不再赘述；但BDS具有星座异构、GEO卫星机动频繁、地面运控监测站难以全球均匀分布等特点，导致BDS卫星精密定轨具有其特殊性，理论尚待完善[4]。

由于BDS尚未实现全球服务，区域测站对卫星跟踪的连续性和几何结构差，BDS精密定轨多采用BDS/GPS联合定轨方法以充分利用关联信息，提高BDS定轨精度[10]。基于地面监测站的BDS/GPS联合定轨可以实现径向精度优于10 cm的BDS精密定轨[11]。通过适当方法进行模糊度固定后，IGSO/MEO卫星径向精密定轨精度可达到约5 cm[12-13]。太阳光压摄动模型是对BDS精密定轨影响最大的动力学模型，采用ECOM 5参数简化模型的IGSO/MEO卫星定轨精度优于ECOM 9参数完整模型，均方根(root mean square，RMS)优于20 cm；通过对光压模型的改进可进一步提高BDS卫星零偏期间的轨道解算精度[14-16]。对卫星姿态、卫星天线相位中心和地影状态等进行深入研究对提升BDS卫星精密定轨水平有较大意义[17]。GEO卫星精密定轨是BDS系统建设的难点之一，主要包括精密测距定轨、精密测角定轨、天基精密测距测速及联合测轨技术[18]。顾及系统误差的GEO卫星定轨可极大削弱系统误差，提高定轨精度[19]：针对GEO卫星轨道频繁机动的特点，建立GEO卫星轨道机动算法和模型，对机动后的GEO卫星进行轨道解算及预报，快速得到机动后的GEO卫星精密轨道[20-22]。中国区域地面运控监测站无法实现卫星的全弧段跟踪，采用先验信息可改善区域站定轨精度[23-24]；但同时削弱了观测数据对轨道的约束作用[25]。

综上所述，针对BDS卫星精密定轨的研究主要集中在多模GNSS联合定轨、BDS模糊度固定方法、精化BDS太阳光压参数模型等动力学模型、提高GEO卫星定轨精度和地面区域监测站测定卫星轨道等方面，而未从根本上彻底解决GEO卫星几何结构差和区域地面运控监测站无法长弧段连续跟踪IGSO和MEO卫星的难题。GEO卫星定轨精度差的主要原因是其空间几何构型较差，与其它参数的相关性强，导致参数很难精确求解。IGSO和MEO卫星主要受限于测站区域分布，难以实现卫星全弧段多重覆盖。低轨卫星星载BDS接收机作为高动态的天基监测站增强地面区域监测站，可以改善BDS卫星几何构型，同时可以增加天地监测网对IGSO/MEO卫星的跟踪弧长，有利于解决上述问题。下面简要总结下低轨卫星星载GNSS技术的进展。

2 低轨卫星星载GNSS技术进展

1982年，美国首先采用星载GPS技术测定低轨卫星轨道。由于受到重力场模型差和电离层的影响，其定轨精度较低。1992年，海洋测高卫星(Topex/Poseidon，T/P)首次实现了低轨卫星星载GPS技术精密定轨。受此鼓舞，随后发射的CHAMP(challenging minisatellite payload)、GRACE(gravity recovery and climate experiment)、GOCE(gravity field and steady-state ocean circulation explorer)和海洋二号等几十颗低轨卫星上均搭载了星载GPS双频接收机，中国的风云三号卫星上同时搭载了GPS和BDS接收机。目前，星载GNSS技术已成为低轨卫星精密定轨的主要手段。

低轨卫星的观测方程数学模型描述为

Lleo=Fleo(Xgns,Xleo,Xoth,t)+εleo。

(3)

式中：Lleo为低轨卫星的GNSS观测数据；Fleo为低轨卫星观测函数；Xgns、Xleo和Xoth分别为GNSS卫星轨道参数、低轨卫星轨道参数和其他待估参数；t为时间；εleo为低轨卫星观测噪声。

低轨卫星在电离层中高速运行，采用改进的数据质量控制方法，提高粗差和周跳探测能力和数据质量控制水平[26]。针对低轨卫星星载GNSS技术精密定轨，国内外专家进行了深入的研究。在T/P、CHAMP、GRACE和GOCE等卫星上的试验结果表明，采用星载GPS观测数据，利用动力学法、几何定轨法或简化动力学法，结合适当数据处理技术，可实现低轨卫星cm级精密定轨[27-30]。我国自主研制和管理的海洋二号卫星，利用在轨校正的低轨卫星星载GPS接收天线相位中心修正可得到cm级的精密轨道[31]。基于风云三号的星载GPS观测数据的定轨精度径向为cm级，3维方向优于10 cm；但是由于观测数据质量稍差，基于星载BDS观测数据的定轨精度偏低。

低轨卫星星载GNSS技术受限时，可采用其他精密定轨技术以提高低轨卫星轨道精度，主要包括卫星激光测距(satellite laser ranging，SLR)、星基多普勒轨道确定和无线电定位组合系统(doppler orbitography and radio-positioning integrated by satellite，DORIS)、精密测距测速系统(precise range and range rate equipment，PRARE)等[32]。SLR具有测量精度高、速度快、系统误差小、抗干扰性强等优点；但是布站代价大、观测资料少、观测台站分布不理想、时间空间覆盖率低、受气候影响大、操作难度大、无法得到岁差章动改正。目前，SLR的测距精度为cm级，正在向mm级发展，常用于检核卫星定轨精度[33]。DORIS可实现全球跟踪测量，精度高、可靠性强。目前，DORIS系统可用于200 km到2 000 km的低轨道卫星，其径向误差为cm级，期望将来可用于较高轨道卫星[34]。PRARE是一种双频双程微波跟踪系统，可精确测量卫星与地面站之间的距离及其变化率，具有全天候、全自动、观测数据密集、地面站易于流动、时空覆盖率广等优点；但目前应用较少、定轨精度相对偏低，尚未用于导航卫星。利用PARAE测定的ERS-2卫星径向精度约为5 cm，3维精度为dm级[35]。

综上所述，随着设备制造和定轨技术的不断进步，星载GNSS技术定轨精度不断提升。目前，低轨卫星星载GPS定轨精度已达到cm级，可以作为导航卫星精密定轨的动态监测站；但是没有针对星载BDS观测数据质量和定轨方法的系统性研究与分析：可使用其他技术进行低轨卫星定轨，提高其轨道精度，进而增强地面监测站的BDS轨道解算精度。

3 低轨卫星增强GPS卫星定轨技术进展

国际上部分学者提出了利用低轨卫星星载GPS观测数据联合地面监测站数据综合测定GPS卫星轨道的技术，实现过程如下：将GPS和LEO卫星运动方程用卫星位置矢量、速度矢量和动力学参数表示为初值问题和变分方程，积分后可得到状态转移矩阵；同时将地面监测站和低轨卫星观测方程线性化，合理平衡几何观测信息和动力学信息[36-37]。得到地面监测站和低轨卫星GPS观测数据联合定轨的简化动力学观测模型[38]为

(4)

星载GNSS技术测定低轨卫星轨道方法分为“两步法”和“一步法”。“两步法”的第一步基于地面监测站解算GNSS卫星轨道钟差，第二步利用解算的GNSS卫星精密轨道钟差，基于低轨卫星星载GNSS观测数据测定LEO卫星轨道。“一步法”基于地面监测站和天基低轨卫星的GNSS观测数据，统一解算GNSS卫星轨道、低轨卫星轨道和地球自转参数等。“一步法”联合定轨提出的最初目的是提高星载GPS技术测定低轨卫星轨道精度；但是相对于“两步法”，“一步法”联合定轨对LEO卫星定轨精度改进不明显，在径向和切向分量精度略有提升[39]。国内外专家进一步分析“一步法”在CHAMP、GOCE等低轨卫星精密定轨中的应用，结果显示“一步法”联合定轨可改进GPS卫星轨道、地球自转参数和坐标框架，加强解的强度[40-43]；因为在“一步法”联合定轨中，低轨卫星作为高动态的天基监测站增强地面监测网，增加了观测数据量和长基线跟踪几何。鉴于低轨卫星和地面监测站观测数据联合定轨具有优势，2000年至2010年，IGS成立了LEO工作组，联合多家分析中心研究如何利用LEO GNSS数据增强IGS产品。研究结果表明，低轨卫星增强传统地面监测网可改善跟踪几何构型，减少接收机扰动，实现地球自转参数的去相关。区域地面监测站和低轨卫星联合定轨以增强GNSS卫星轨道的优势更为明显，可极大改善导航卫星的几何构型，增加有效观测弧段长度，提高导航卫星定轨精度[44]。

综上所述，低轨卫星增强地面监测站测定GPS卫星精密轨道技术可有效提高GPS卫星精密定轨的精度和可靠性。

4 低轨卫星联合地面监测站测定BDS卫星精密轨道技术

BDS起步较晚，尚无公开的低轨卫星星载BDS实测数据，低轨卫星增强BDS精密定轨的研究成果较少；但是从理论上分析，低轨卫星和地面监测站联合测定BDS卫星轨道可极大提高BDS卫星，特别是GEO卫星的精密定轨精度，并解决BDS测站区域分布的问题。

目前，BDS GEO卫星的精密定轨精度为m级，远低于IGSO/MEO卫星dm级的轨道精度，将影响GEO卫星在系统服务中发挥其显著优势。BDS卫星轨道精度不均匀是其他卫星导航系统未曾遇到过的问题；提高GEO卫星定轨精度，实现BDS异构星座精度水平一致，对BDS建设具有重大意义。GEO卫星相对地面运控监测站在一个很小的窗口范围内活动，地面监测站网络对GEO卫星的观测几何构型基本保持不变是GEO卫星定轨精度差的根本原因。因此仅仅依靠地面监测站数据无法从根本上解决GEO卫星定轨精度差的问题，改善GEO卫星与测站的几何构型是提高其定轨精度的关键技术。

低轨卫星高度约为400～900 km，周期约为1.5 h到2 h。1个GEO运行周期内，低轨卫星约跟踪通过14个周期，因此，低轨卫星星载BDS的观测数据充分。地面运控监测站的坐标精度已达到mm级或亚cm级，考虑到低轨卫星受到对流层延迟和多路径效应等部分误差影响较小，其位置精度达到cm级即可作为高精度的天基监测站。天基监测站和地面监测站联合测定BDS GEO卫星轨道，将极大改善站星几何构型，削弱切向轨道与相位模糊度的相关性，从而大大提高GEO卫星的定轨精度，特别是切向方向的轨道精度。

BDS地面运控系统的首要任务是生成基于地面运控监测站的广播星历[6]；但是受政治因素和国土面积等因素的影响，BDS地面运控监测站难以像GPS一样在全球范围内形成均匀分布的监测网。虽然BDS在积极推进海外建站，然而可控的BDS一级和二级地面运控监测站还是均分布在中国境内。相对于全球地面监测网，中国区域地面监测网难以对BDS IGSO和MEO卫星形成较长弧段的连续的多重覆盖观测，而且区域监测网与卫星的几何构型差。上述原因导致基于地面运控监测站观测数据的BDS IGSO和MEO卫星定轨精度差。BDS区域系统星下点轨迹和中国区域监测站网络示意如图1所示。

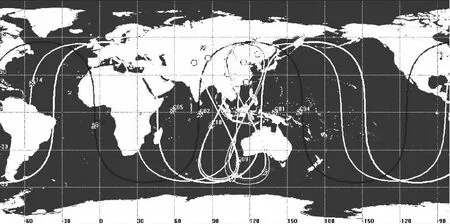
图1 BDS区域系统星下点轨迹和中国区域监测站分布示意

低轨卫星天基监测站观测数据可以有效弥补区域监测网在空间覆盖上的不足并改善站星几何结构，从而提高基于区域监测网的IGSO和MEO卫星定轨精度。GEO/IGSO/MEO/LEO相对分布如图2所示。

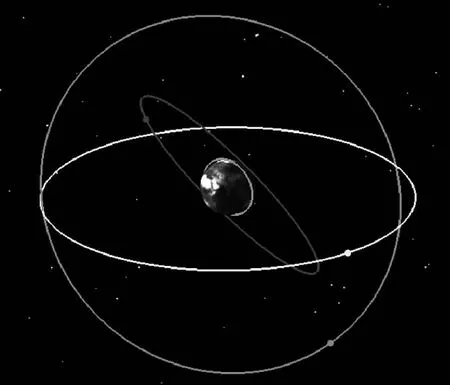
图2 GEO/IGSO/MEO/LEO相对分布示意

低轨卫星联合地面监测站测定BDS卫星精密轨道技术路线可描述为：首先同时对地面监测站和低轨卫星星载BDS观测数据进行数据预处理，获取干净的BDS观测数据；然后通过BDS广播星历和观测数据获取BDS卫星和低轨卫星的初始轨道和卫星动力学轨道参数；再将地面监测站和低轨卫星星载BDS观测数据联合处理，同时解算BDS卫星轨道钟差、LEO卫星轨道和其他参数；迭代进行参数估计和残差编辑后，最终解算得到BDS和LEO卫星实测轨道参数。进行轨道外推即可获得预报轨道参数。具体技术路线如图3所示。

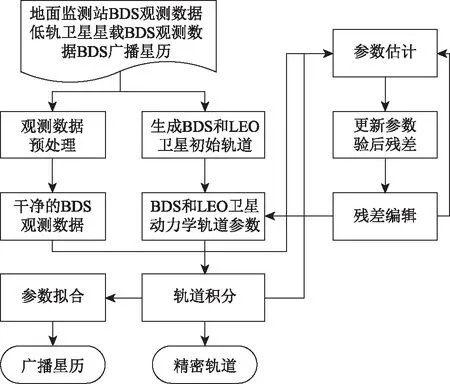
图3 低轨卫星联合地面监测站测定BDS卫星精密轨道技术路线

5 实验与结果分析

考虑到尚无公开的星载BDS观测数据，本文基于中国区域监测站验证低轨卫星同地面监测站联合测定GPS卫星轨道的增强效果，设计对比方案如下：

方案1：利用中国及周边区域分布的7个地面监测站(如图4所示)的GPS观测数据，测定GPS卫星轨道。

方案2：利用方案1的地面观测值，加入GRACE 2颗卫星星载GPS观测数据，联合测定GPS卫星轨道。

图4 区域监测站分布

以国际GNSS服务组织(International GNSS Service，IGS)公布的最终轨道作为基准，得到方案1和方案2的卫星轨道坐标系径向切向法向(radial tangential normal directions，RTN)的轨道精度对比分别如图5～图7所示。

图5 轨道径向分量精度

图6 轨道切向分量精度

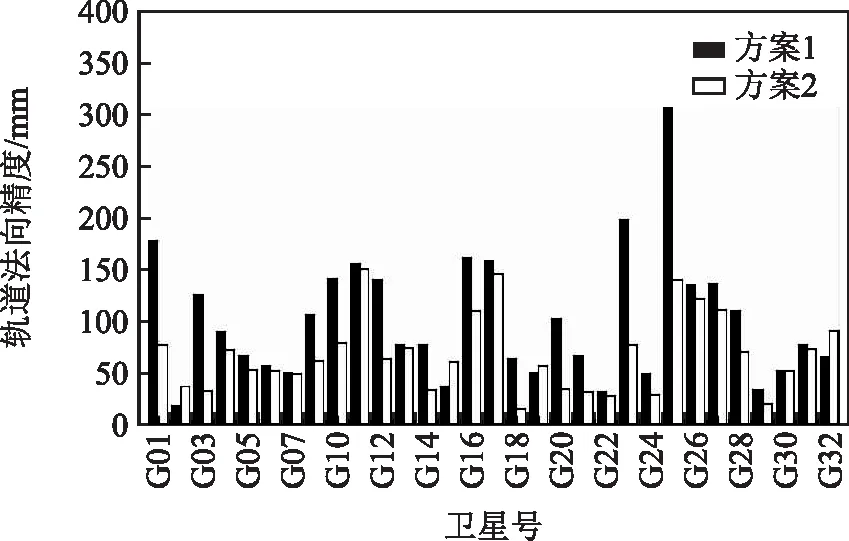
图7 轨道法向分量精度

方案1的RTN方向轨道精度分别为258、219和100 mm，方案2的RTN方向精度分别为174、138和68 mm，加入2颗低轨卫星后，地面区域监测网定轨精度在RTN方向上分别提升32 %、37 %和32 %。钟差精度由0.39提高到0.32 ns，提

升了18 %。分析原因为：地面区域监测站跟踪GPS卫星的有效观测弧段较短且几何结构较差，加入低轨卫星GPS观测数据后，可有效增加GPS卫星的有效观测弧段长度，改善卫星几何构型，从而极大提升GPS卫星的定轨精度。

6 结束语

低轨卫星增强地面区域监测网测定GNSS卫星精密轨道能够极大改善测站与卫星的几何构型、增加有效观测弧长，进而提高GNSS卫星定轨精度。

BDS拟采用的区域地面站联合导航卫星间的星间链路来提高导航系统空间信号精度的方案严重依赖于导航卫星间的星间链路的可靠性和稳定性，有极大的风险，应慎重引入。利用低轨卫星数据增强地面区域监测站观测数据可以作为星间链路的备份。

低轨卫星增强地面区域监测站测定BDS卫星精密轨道技术可以弥补境外建站困难，减少地面监测站的布设数量，大大提高跟踪弧段；有效增强星座的几何结构，特别是对于GEO卫星，可优化空间几何构型，提高定轨精度；从而显著提升BDS的服务性能。

由于低轨卫星数量众多，充分利用低轨卫星资源，同时结合导航卫星、通讯卫星，可以为未来天基PNT体系的全面设计和构建提供支持。

低轨卫星增强地面监测站测定BDS卫星精密轨道在带来优势的同时，也增加了数据处理的复杂性和其他技术问题，主要有：1)低轨卫星增强BDS精密定轨需要顾及高频钟差，计算量大幅提升；2)目前尚未实现观测数据的实时传输；3)尚未有公开的星载BDS观测数据，研究工作更是仅停留在理论或仿真层面。

[1] 杨元喜，李金龙，王爱兵，等.北斗区域卫星导航系统基本导航定位性能初步评估[J].中国科学：地球科学，2014，44(1)：72-81.

[5] 杨元喜，李金龙，徐君毅，等.中国北斗卫星导航系统对全球PNT用户的贡献[J].科学通报，2011，56(21)：1734-1740.

[3] 葛茂荣，刘经南.GPS卫星精密星历的实时确定[J].武汉测绘科技大学学报，1999，24(1)：32-35.

[4] 刘伟平，郝金明.北斗卫星导航系统精密轨道确定[M].北京：测绘出版社，2016.

[5] 郭金运，孔巧丽，常晓涛，等.低轨卫星精密定轨理论与方法[M].北京：测绘出版社，2014.

[6] HABRICH H.Geodetic applications of the global navigation satellite system(GLONASS)and of GLONASS/GPS combination[D].Bern：Astronomical Institute University of Bern，1999.

[7] SCHUTZ B，TAPLEY B，ABUSALI P，et al.Dynamic orbit determination using GPS measurements from TOPEX/POSEIDON[J].Geophys Res Lett，1994(19)：2179-2182.

[8] YUNCK T P，BERTIGER W I，WU S C，et al.First assessment of GPS-based reduced dynamic orbit determination on Topex/Poseidon.Geophysical Research Letters，1994(21)：541-544.

[9] WU S C，YUNCK T P，THORNTON C L.Reduced-dynamic technique for precise orbit determination of low earth satellites[J].Guidance Control and Dynamics，1991，14：24-30.

[10] 李敏.多模GNSS融合精密定轨理论及其应用研究[D].武汉：武汉大学，2011.

[11] ZHAO Q L，GUO J，LI M，et al.Initial results of precise orbit and clock determination for compass navigation satellite system[J].Journal of Geodesy，2013，87(5)：475-486.

[12] HE L N，GE M R，WANG J X，et al.Experimental study on the precise orbit determination of the BeiDou navigation satellite system[J].Sensors，2013，13：2911-2928.

[13] 刘伟平，郝金明，李建文，等.多GNSS融合的北斗卫星精密定轨[J].测绘学报，2014，43(11)：1132-1138.

[14] LOU Y D，LIU Y，SHI C，et al.Precise orbit determination of BeiDou constellation based on BETS and MGEX network[J].Scientific Reports，2014，4(4692)：1-10.

[15] 郭靖.姿态、光压和函数模型对导航卫星精密定轨影响的研究[D].武汉：武汉大学，2014.

[16] LIU J，GU D，JU B，et al.Basic performance of BeiDou-2 navigation satellite system used in LEO satellites precise orbit determination[J].Chinese Journal of Aeronautics，2014，27(5)：1251-1258.

[17] 毛悦，宋小勇，贾小林，等.北斗导航卫星地影状态分析[J].测绘学报，2014，43(4)：353-359.

[18] 杜兰.GEO卫星精密定轨技术研究[D].郑州：信息工程大学，2006.

[19] 徐天河，贺凯飞.顾及系统误差的GEO卫星几何法定轨[J].大地测量与地球动力学，2009，29(1)：64-69.

[20] CAO F，YANG X，LI Z，et al.Orbit determination and prediction of GEO satellite of BeiDou during repositioning maneuver[J].Advances in Space Research，2014，54(9)：1828-1837.

[21] 郭睿，周建华，胡小工，等.一种地球静止轨道卫星的快速恢复定轨方法[J].测绘学报，2011，40(增刊1)：19-25.

[22] 华爱辉.机动情况下的GEO卫星定轨方法研究[D].西安：中国科学院国家授时中心，2008.

[23] 周善石，胡小工，吴斌.区域监测网精密定轨与轨道预报精度分析[J].中国科学：物理学 力学 天文学，2010，40(6)：800-808.

[24] 赵齐乐，耿涛，李俊义，等.历史轨道约束信息下的区域站GPS卫星轨道确定[J].大地测量与地球动力学，2009，29(5)：81-84.

[25] 楼益栋，姚秀光，刘杨，等.模糊度固定与弧段长度对区域站定轨的影响分析[J].武汉大学学报(信息科学版)，2016，41(2)：249-254.

[26] 韩保民.基于星载GPS的低轨卫星几何法定轨理论研究[D].武汉：中国科学院测量与地球物理研究所，2003.

[27] JAGGI A，HUGENTOBLER U，BEUTLER G.Pseudo-stochastic orbit modeling techniques for low-earth orbiters[J].Journal of Geodesy，2006，80(1)：47-60.

[28] YANG Y，YUE X，YUAN J，et al.Enhancing the kinematic precise orbit determination of low earth orbiters using GPS receiver clock modelling[J].Advances in Space Research，2014，54(9)：1901-1912.

[29] BOCK H，JAGGI A，MEYER U，et al.GPS-derived orbits for the GOCE satellite[J].Journal of Geodesy，2010，85(11)：807-818.

[30] 张兵兵，聂琳娟，吴汤婷，等.SWARM卫星简化动力学厘米级精密定轨[J].测绘学报，2016，45(11)：1278-1284.

[31] 郭靖.利用星载GPS观测数据确定海洋2A卫星cm级精密轨道[J].武汉大学学报(信息科学版)，2013，38(1)：52-55.

[32] OLIVER M，EBERHARD G.卫星轨道-模型、方法和应用[M].王家松，祝开建，胡小工，等译.北京：国防工业出版社，2012.

[33] 李洪波，彭军.SLR技术及其在GPS卫星定轨中的应用[J].计测技术，2013(6)：11-15.

[34] 李培佳，曹建峰，胡小工，等.利用DORIS测轨系统实现高精度定轨[J].飞行器测控学报，2010，29(3)：58-64.

[34] 张飞鹏.PRARE及其应用于ERS-2精密定轨的研究[D].上海：中国科学院上海天文台，2000.

[36] 李济生.人造卫星精密轨道确定[M].北京：解放军出版社，1995.

[37] 赵齐乐.GPS导航星座及低轨卫星的精密定轨理论和软件研究[D].武汉：武汉大学，2004.

[38] 王乐，张勤，黄观文，等.区域监测站与低轨卫星数据联合测定MEO卫星轨道[J].测绘学报，2016，45(增刊2)：101-108.

[39] HUGENTOBLER U，JAGGI A，SCHAER S，et al.Combined processing of GPS data from ground station and LEO receivers in a global solution[EB/OL].[2017-02-28].https：//www.researchgate.net/profile/A_Jaeggi/publication/226465594_Combined_Processing_of_GPS_Data_from_Ground_Station_and_LEO_Receivers_in_a_Global_Solution/links/00b4951932c60dfc16000000.pdf?inViewer=true&disableCoverPage=true&origin=publication_detail.

[40] ZHU S，REIGBER C，KONIG R.Integrated adjustment of CHAMP，GRACE，and GPS data[J].Journal of Geodesy，2004，78(1)：103-108.

[41] ZHU S Y，MASSMANN F H，YU Y，et al.Satellite antenna phase center offsets and scale errors in GPS solutions[J].Journal of Geodesy，2003，76(11)：668-672.

[42] BOOMKAMP H，DOW J.Use of double difference observations in combined orbit solutions for LEO and GPS satellites[J].Advances in Space Research，2005，36(3)：382-391.

[43] 耿江辉.联合地面和星载数据精密确定GPS卫星轨道[J].武汉大学学报(信息科学版)，2007，32(10)：906-909.

[44] 冯来平.联合低轨卫星和地面监测站数据确定导航卫星轨道[J].大地测量与地球动力学，2016，36(10)：864-869.

DiscussionontechnologyofBDSsatelliteorbitdeterminationenhancedbyLEOsatellites

WANGLe，YANXingyuan，ZHANGQin，HUANGGuanwen，QINZhiwei

(College of Geological Engineering and Geomatics，Chang’an University，Xi’an 710000，China)

Aiming at the problems that geometric configuration between BDS GEO satellites and ground monitoring stations changes slowly，resulting in poor geometric structure and low orbiting accuracy of GEO，and it is difficult for the regional ground monitoring stations in China to observe the BDS IGSO and MEO satellites continuously，leading to shorter effective observation arc and lower orbiting precision，comparing with the orbit determination based on global ground monitoring stations，which impacts the service performance of BDS broadcast ephemeris，the paper discussed a technology that the LEO satellites with spaceborne GNSS recievers were used as high dynamic monitoring stations for the precise orbiting of BDS，combining with ground regional monitoring stations to calculate BDS satellite orbit and clock errors and LEO satellite orbit parameters and so on at the same time.Experimental result showed that the technology could greatly improve the spatial geometrical structure between the stations and satellites，increase the effective observation arc length，achieve overlapping coverage observation，and then enhance the determination accuracy of the three types of BDS orbits and finally promote the performance of BDS service.

BDS；LEO；ground monitoring stations；precise orbiting；broadcast ephemeris

2017-03-27

国家自然科学基金项目(41304033，41674001)；二代导航重大专项课题(GFZX0301040308)；陕西省自然科学基金项目(2016JQ4011)；陕西省自然科学基础研究计划资助项目(2016JM4005)。

王乐(1986—)，男，山东蓬莱人，博士研究生，研究方向为卫星精密定轨。

张勤(1958—)，女，陕西西安人，博士，教授，研究方向为GNSS数据处理等。

王乐，燕兴元，张勤，等.低轨卫星增强BDS卫星定轨技术探讨[J].导航定位学报，2017，5(4)：51-57.(WANG Le，YAN Xingyuan，ZHANG Qin，et al.Discussion on technology of BDS satellite orbit determination enhanced by LEO satellites[J].Journal of Navigation and Positioning，2017，5(4)：51-57.)

10.16547/j.cnki.10-1096.20170411.

P228

A

2095-4999(2017)04-0051-07