多卫星系统频间偏差预报模型分析

韩雪丽，党亚民，王 虎，王 健

(1.中国测绘科学研究院，北京 100830；2.山东科技大学 测绘科学与工程学院，山东 青岛 266510)

多卫星系统频间偏差预报模型分析

韩雪丽1，2，党亚民1，王 虎1，王 健1，2

(1.中国测绘科学研究院，北京 100830；2.山东科技大学 测绘科学与工程学院，山东 青岛 266510)

针对卫星频间偏差参数缺失的问题，采用二次多项式拟合法对缺失的卫星频间偏差参数进行短期及长期预报，以预报值代替真实值：通过构建电离层延迟模型求解各卫星频间偏差参数，统计中国测绘科学研究院iGMAS分析中心各GNSS卫星2016-01—2016-12频间偏差参数解算的结果，与IGS欧洲定轨中心CODE提供的频间偏差数据作对比分析，采用二次多项式拟合法对频间偏差参数进行长期预报及精度分析；并采用类似方法统计分析2017-02-01—2017-02-28的频间偏差参数，分析其短期特性，对未来几天内各卫星的频间偏差参数进行预报及精度分析。实验结果表明，二次多项式拟合方法可以较好地对GPS卫星的频间偏差参数进行预报，为GLONASS卫星及BDS卫星的频间偏差求值及预报提供参考。

GNSS；电离层；球谐函数；频间偏差；预报

0 引言

硬件延迟偏差也称为差分码偏差(differential code biases，DCB)，代表全球卫星导航系统(global navigation satellite system，GNSS)中卫星和接收机不同频率之间或者相同频率不同码之间的硬件延迟偏差，文献[1-3]提出它是卫星导航数据处理中不可忽略的误差项之一。文献[4-5]提出卫星发射之前会对频间偏差参数进行标定，然而在各因素影响下，频间偏差参数会产生漂移现象。

美国选择可用性(selective availability，SA)政策取消后，卫星频间偏差参数对定位及授时精度的影响日趋显著，频间偏差参数的探究及确定变得越发重要。文献[6]提出目前国际上主要有欧洲定轨中心(The Center for Orbit Determination in Europe，CODE)、美国喷气动力实验室(Jet Propulsion Laboratory，JPL)、欧洲空间局(European Space Agency，ESA)等分析中心从事电离层延迟日常数据处理和产品分布。国内则主要有武汉大学、上海天文台、中国测绘科学研究院(Chinese Academy of Surveying and Mapping,CASM)等单位开展了相关研究。

通常在解算频间偏差参数时需令所有测站或卫星频间偏差之和为0，然而当某一卫星频间偏差缺失时，其他各卫星的频间偏差参数之和仍设为0，则该缺失的卫星频间偏差参数值被看作0，这显然是不符合逻辑的。为研究各卫星频间偏差参数长期及短期的变化特性，在某卫星频间偏差参数缺失时，对该卫星频间偏差参数进行短期和长期预报，以预报值代替真实值。本文利用中国测绘科学研究院国际GNSS监测评估系统(international GNSS monitoring and evaluation system，iGMAS)分析中心及CODE数据，对频间偏差参数展开研究，以更好地为导航定位服务。

1 电离层延迟建模

根据文献[5-10]提出的利用双频数据无几何组合可获得垂向电子总含量(vertical total electric content，VTEC)，公式为

(1)

式中：VTEC为卫星到接收机电离层穿刺点的垂向总电子含量；ΔP为双频无几何观测值；c为光在真空中的传播速度；DCBr和 DCBs分别为接收机频间偏差及卫星频间偏差；F(z)为电离层投影函数；f为双频伪距之差转换为总电子含量的频率相关系数，其中，对全球定位系统(global positioning system，GPS)卫星而言f取9.524 37，北斗卫星导航系统(BeiDou navigation satellite system，BDS)卫星f取8.993 2。

文献[11-12]提出的球谐函数模型，公式为

(2)

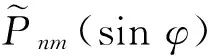
双频无几何组合观测值扣掉频间偏差即可转换成VTEC，添加适当的基准条件可求解频间偏差参数值。

2 数据处理与分析

2.1 数据选取与处理策略

本文选取中国测绘科学研究院iGMAS中心的频间偏差数据及欧洲定轨中心CODE数据，对2016年GNSS各卫星各月份频间偏差参数进行统计。

表1 求解全球电离层估计策略

2.2 约束条件及处理方法

由于式(1)秩亏无法直接求解，法方程求逆前需添加约束条件，以分离各类相关性强的参数，确保法方程能够满秩进行正常解算。常用的确保法方程满秩的方法有3种：1)将其中某一个值固定；2)零均值条件；3)将先验值和方差作为虚拟观测值加入法方程。鉴于卫星频间偏差值变化相对稳定且变化较慢，因此通常把1 d内的卫星频间偏差当做定值。双频无几何组合观测值扣掉频间偏差转换成VTEC后，为了将频间偏差参数与钟差分离，需添加适当的基准条件。频间偏差参数基准的确定可以通过以下3种方法实现：1)假设某一接收机或某卫星端频间偏差为0；2)令所有测站频间偏差之和为0或所有卫星的频间偏差之和为0；3)给所有频间偏差一个先验值和适合的先验方差，作为虚拟观测值叠加到法方程中。

2.3 精度解析

2.3.1 2016年精度解析

利用IGS、中国测绘科学研究院iGMAS分析中心数据解算频间偏差产品，以IGS 频间偏差产品(CODE)为基准进行精度比较。解算结果如图1所示(2016-01—2016-12)，为CASM与CODE作差的结果。其中：横坐标代表月份；纵坐标表示频间偏差，单位为纳秒(ns)；图例表示卫星号。

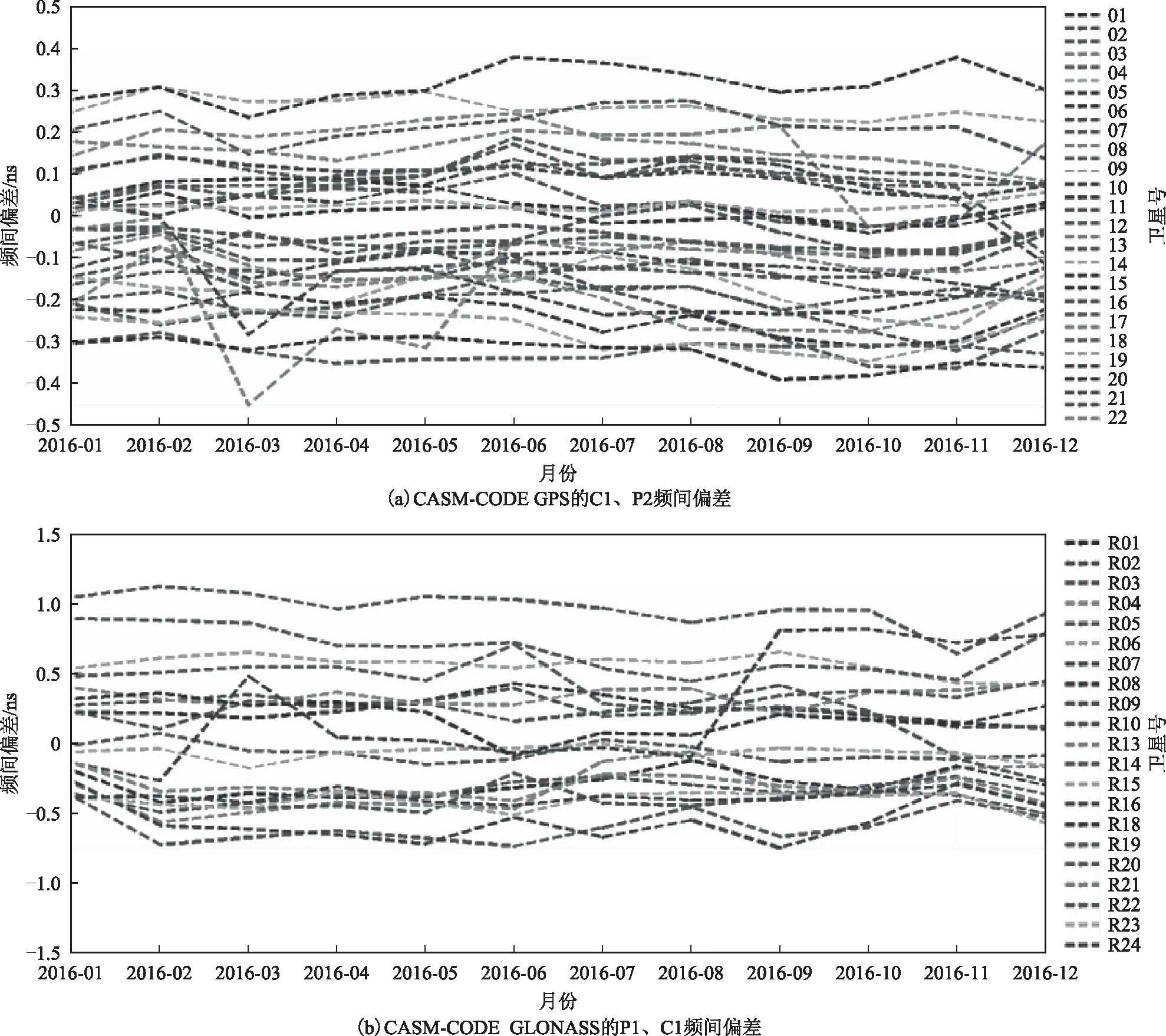
图1 CASM与CODE精度对比

图1中可见：出现异常波动现象往往是由于某一颗或几颗卫星的突然出现或消失导致约束条件发生了变化；二者GPS卫星C1与P2的频间偏差差值均在0.5 ns内，且多数在±0.3 ns范围内波动；格洛纳斯卫星导航系统(global navigation satellite system,GLONASS)卫星P1与C1的频间偏差之差均在1.5 ns内，且多数在在±0.5 ns范围内波动。

2.3.2 2017-02精度解析

同理，以2017-02数据为例，利用IGS、中国测绘科学研究院iGMAS分析中心数据，解算各卫星每日频间偏差参数，并以CODE中心频间偏差产品为基准进行精度比较，具体结果见图2(年积日第031天至第058天)。

由图2可知：中国测绘科学研究院iGMAS分析中心CASM与欧洲定轨中心CODE的GPS卫星P1P2频间偏差之差的解算结果均在1.5 ns范围内，除G28卫星外，其余各卫星频间偏差参数均在±0.5 ns范围内波动，即说明iGMAS分析中心所观测的GPS频间偏差与CODE相比，多数在±0.5 ns范围内波动；同理，CASM与CODE的GLONASS卫星P1、P2频间偏差之差的解算结果均在2 ns范围内，且多数GLONASS卫星的P1、P2频间偏差均在±1 ns范围内波动。

2.4 频间偏差参数预报及精度解析

本文采用iGMAS分析中心2016-01—2016-12数据及2017-02-01—2017-02-28的频间偏差数据，利用二次多项式拟合方法分别对GPS、GLONASS及BDS卫星的1、2个月后的频间偏差参数进行长期预报，及对未来1、2、3 d的频间偏差参数进行短期预报，且对预报精度进行统计分析。精确度采用[1—(预报值-真实值)/真实值]表示，结果保留2位小数。具体统计结果如表2所示。

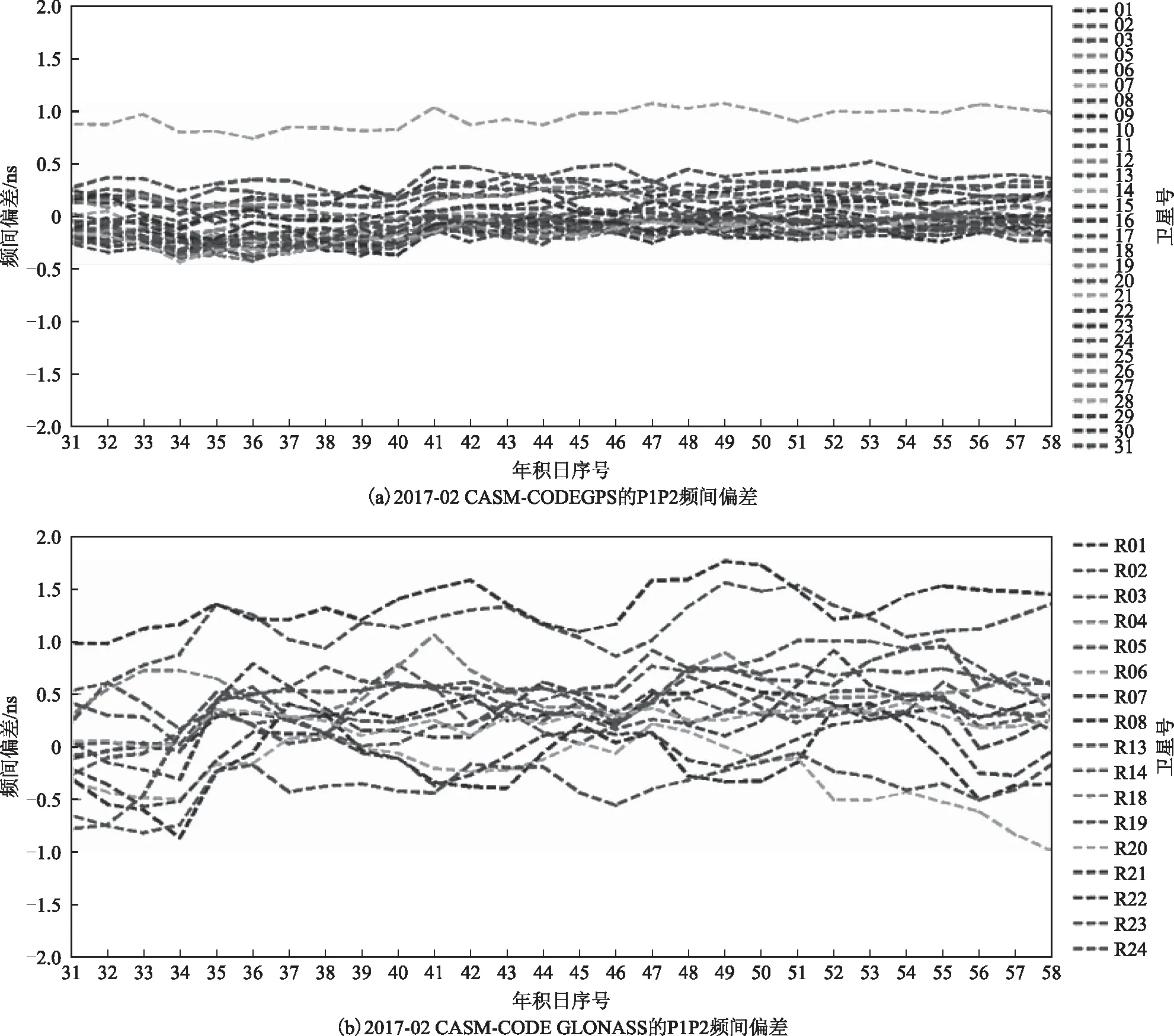
图2 2月份CASM与CODE精度对比

类型卫星号长期预报精度/(%)短期预报精度/(%)1个月2个月1d2d3dGPS卫星长期预报(C1-P2)短期预报(P1-P2)10.991.000.991.001.0020.950.960.980.980.9930.970.990.960.960.9550.910.870.920.960.9860.980.960.980.980.9770.960.940.950.960.9980.981.000.990.980.9890.970.980.970.960.96100.980.990.980.980.98110.960.980.960.970.96120.950.960.950.970.97130.940.970.950.980.96140.960.980.910.910.94

续表

本文采用的拟合方法如下：首先对各卫星2016-01—2016-12数据及2017-02-01—2017-02-28的频间偏差参数进行统计，然后利用matlab程序中的polyfit()函数，采用最小二乘法对各卫星频间偏差参数进行二阶多项式拟合，获得形如y=ax2+bx+c的多项式系数a、b、c，将系数代入公式即可获得各卫星频间偏差参数随时间变化的二次多项式。预报时，只需将所需预报天数当做未知数分别带入求值即可。各卫星长短期频间偏差预报方法类似。

首先，本文针对GPS卫星C1-P2的频间偏差进行了长期预报，对P1-P2的频间偏差进行了短期预报。观察GPS卫星长期及短期预报精度结果，可发现GPS卫星长期预报精确度均在87 %以上，而短期预报精度比长期精度略低，也均在83 %以上。某些卫星的短期预报值准确度高，某些卫星则长期预报值精度更高。

针对GLONASS卫星，对C1-P2的频间偏差进行了长期预报，对P1-P2的频间偏差进行了短期预报。然而GLONASS卫星的预报精度与GPS卫星相比，异常值较多，且易出现某几颗卫星预报准确率较低的情况。虽然如此，仍有较多卫星的预报准确率在70 %以上。

最后，本文对BDS卫星的I2-I6频间偏差进行了长期预报，对I2-I7频间偏差数据进行了短期预报。该数据同样有少数异常值，绝大部分卫星频间偏差准确率在80 %左右。此外，可发现某些BDS卫星的短期预报准确率随时间增加有降低趋势(如7号卫星)，有的则呈相反状态(如4、8及14号卫星)。

综合来看，GPS卫星的频间偏差预报率比其他卫星均高出许多。GLONASS卫星及BDS卫星出现异常值往往是由于某一颗或几颗卫星的突然出现或消失导致约束条件发生了变化所致。可见，利用二次多项式方法可以较好地预报GPS卫星频间偏差的长期及短期数据，对于GLONASS卫星及BDS卫星的频间偏差求值及预报也具有重要的参考作用。因此，当各卫星系统出现某一颗或几颗卫星缺失时，可考虑采用频间偏差预报值代替其真实值，以减少误差，提高导航定位服务的精度。

3 结束语

本文主要通过双频数据无几何组合观测数据及球谐函数建立电离层延迟模型，利用约束条件求解得到GNSS各卫星的频间偏差。将iGMAS分析中心的2016-01—2016-12数据及2017-02-01—2017-02-28的频间偏差数据与IGS欧洲定轨中心CODE的频间偏差产品作对比，分别进行长期及短期预报，并进行准确率验证。实验结果表明，二次多项式拟合方法可以较好地对GPS卫星的频间偏差数据进行预报，对于GLONASS卫星及BDS卫星的频间偏差求值及预报也有重要的参考作用。虽然二次多项式可以对频间偏差参数进行长短期预报，但当卫星频间偏差参数缺失时，基准的改变易引起参数波动，频间偏差参数基准的确定是未来频间偏差研究的重点。

[1] 陈俊勇，党亚民，程鹏飞.全球导航卫星系统的进展[J].大地测量与地球动力学，2007，27(5)：1-4.

[2] 胡玉坤，刘根友，段鹏硕，等.GNSS卫星中DCB的使用方法[J].测绘通报，2016(5)：11-13.

[3] 张宝成，欧吉坤，袁运斌，等.利用非组合精密单点定位技术确定斜向电离层总电子含量和站星差分码偏差[J].测绘学报，2011，40(4)：447-453.

[4] 樊家琛，吴晓莉，李宇翔，等.基于三频数据的北斗卫星导航系统DCB参数精度估计方法[J].中国空间科学技术，2013(4)：447-453.

[5] 秦懿，蔡成林，李思敏.一种GPS/BDS多频单站电离层模型与卫星频间偏差精化方法[J].科学技术与工程，2016(15)：129-133.

[6] 章红平，韩文慧，黄玲，等.地基GNSS全球电离层延迟建模[J].武汉大学学报(信息科学版)，2012，27(10)：1186-1189.

[7] 张小红，李征航，蔡昌盛.用双频GPS观测值建立小区域电离层延迟模型研究[J].武汉大学学报(信息科学版)，2001，26(2)：140-143，159.

[8] 王刚，魏子卿.格网电离层延迟模型的建立方法与试算结果[J].测绘通报，2000(9)：1-2.

[9] 李博峰，葛海波，沈云中.无电离层组合、Uofc和非组合精密单点定位观测模型比较[J].测绘学报，2015，44(7)：734-740.

[10] STEFAN S.Mapping and predicting the Earth’s ionosphere using the global positioning system[D].Bern：Astronomical Institute of the University of Bern，1999.

[11] 李征航，黄劲松.GPS测量与数据处理[M].武汉：武汉大学出版社，2010：97.

[12] 耿长江，唐卫明，章红平.利用CORS系统实时监测电离层变化[J].大地测量与地球动力学，2008，28(5)：105-108.

Analysisonpredictionmodeloffrequencydeviationformultisatellitesystem

HANXueli1，2，DANGYamin1，WANGHu1，WANGJian1，2

(1.Chinese Academy of Surveying and Mapping，Beijing 100830，China；2.Institute of Geomatics，Shandong University of Science and Technology，Qingdao，Shandong 266510，China)

Aiming at the problem of parameter deficiency of satellite frequency deviation，the paper used the two order polynomial fitting method to predict the lacking frequency deviation of the satellite in short and long terms，and replaced the real value with the forecast value：the ionospheric delay model was given to calculate the deviation parameters of each satellite，the results of the frequency deviation(DCB)of the GNSS satellites of the iGMAS Analysis Center of China Academy of Surveying and Mapping from January 2016 to December 2016 were computed，and the data of frequency deviation from CODE of IGS were comparatively analyzed，then the polynomial fitting method was used to predict the DCB parameters and analyze the accuracy for a long time；moreover，by using the similar method，the DCB parameters of 2017-02-01 to 2017-02-28 were analyzed with the short-term characteristics，and those of the coming days were predicted for the satellites.Experimental result showed that the two polynomial fitting method could effectively predict the deviation of frequency of GPS satellites，which would provide a reference for calculate and predict DCB of GLONASS and BDS satellites.

GNSS；ionosphere；spherical harmonic function；frequency deviation；prediction

2017-03-16

国家自然科学基金项目(41474011)；国家自然科学青年基金项目(41404034)；中国博士后基金第59批面上资助项目(2016M590715)。

韩雪丽(1991—)，女，山东阳信人，硕士研究生，研究方向为电离层、GNSS数据处理与应用等。

韩雪丽，党亚民，王虎，等.多卫星系统频间偏差预报模型分析[J].导航定位学报，2017，5(4)：30-35.(HAN Xueli，DANG Yamin，WANG Hu，et al.Analysis on prediction model of frequency deviation for multi satellite system[J].Journal of Navigation and Positioning，2017，5(4)：30-35.)

10.16547/j.cnki.10-1096.20170407.

P228

A

2095-4999(2017)04-0030-06