基于样本噪声检测的AdaBoost算法改进①

张子祥,陈优广

(华东师范大学 计算机科学与软件工程学院,上海 200333)

基于样本噪声检测的AdaBoost算法改进①

张子祥,陈优广

(华东师范大学 计算机科学与软件工程学院,上海 200333)

针对传统的AdaBoost算法中,存在的噪声样本造成的过拟合问题,提出了一种基于噪声检测的AdaBoost改进算法,本文称为NAdaBoost(nois-detection AdaBoost). NAdaBoost算法创新点在于针对传统的AdaBoost算法在错误分类的样本中,噪声样本在某些属性上存在很大差异,根据这一特性来确定噪声样本,再重新使用算法对两类样本进行分类,最终达到提高分类准确率的目的. 本文对二分类问题进行实验结果表明,本文提出的算法和传统的AdaBoost算法,以及相关改进的算法相比,有较高的分类准确率.

过拟合; 噪声检测; AdaBoost算法; 二分类

1 引言

历史上,Kearns 和 Valiant[1,2]首先提出“强可学习(Strong learnable)”和“弱可学习 (Weakly learnable)”的概念,指出在概率近似正确 (Probably approximately correct,PAC)的学习框架中,“弱可学习”可以转化为“强可学习”. Schapire 后来证明在该框架下[3],一个概念是强可学习的充分必要条件是这个概念是弱可学习的. 1995 年 AdaBoost (Adaptive Boosting)算法被提出,在机器学习中得到了广泛的运用,其中在文本分类[4]和人脸检测[5]上取得比较成功的应用,并且它是第一个实现实时人脸检测的算法,与以前的很多算法相比,它在速度上有很大的突破,因此研究该算法不论是在机器学习还是图像处理方面都具有非常广阔的前景.

AdaBoost算法跟大多数其它学习算法相比,不会很容易出现过拟合现象,但AdaBoost算法对噪声和异常数据很敏感,在有噪声的情况下会出现过拟合[6],这是由于噪声样本在不断迭代的情况下,权值不断增加,进而分类器的准确率会有所下降. 目前提出了一些方法来减弱噪声的影响,一类方法是修改损失函数,在不断的迭代过程中噪声点权重下降[7],相对比较好的算法是LogitBoost. 这类方法在一定程度上取得了效果,但也对正常训练样本的权重产生影响. Yunlong提出了EAdaBoost算法[8],处理样本中存在的噪声样本,以此来提高算法的准确率,此外还有学者将多个算法结合起来如MutiboostingAB[9]等. 可见在噪声数据方向的研究对于AdaBoost算法的改进还有很大的空间,同样算法的改进对于文本分类和人脸检测等问题的解决,具有重大意义,本文将针对AdaBoost算法对噪声和异常数据很敏感这一问题进行深入的研究.

综上所述本文的创新点是从处理样本噪声来对AdaBoost算法进行研究和改进. 首先在第一节介绍AdaBoost算法和相关分析,第二节对提出的新算法进行详细的介绍和分析,第三、四节是实验总结部分.

2 AdaBoost算法介绍

AdaBoost算法的主要目的就是把弱分类器组合形成一个强分类器.

2.1 算法流程

算法1. AdaBoost算法输入: 训练数据集(二分类); 弱学习算法输出: 最终分类器G(x)1. 初始化训练数据的权值分布. 所有的训练样本开始时都赋值一样的权重: 1/N2. 进行多轮迭代(1,2,….,M)a) 使用上一步得到的Dm训练数据集进行学习,可以得到一个基本分类器:b) 计算Gm分类的误差率:c) 计算的系数,表示在最终分类器中起的重要程度.d) 更新训练数据集的权值分布如果em>1/2,结束迭代. 其中,3. 构建基本分类器的线性组: 得到最终的分类器: ()

AdaBoost算法主要是以迭代的方式不断增大被错误判断样本的权值的原则,来进行样本权值的更新,分类器在下一次分类中把重心放在那些被错误判断的样本上,从而达到正确分类所有样本的目的,多个这样的分类器会被算法训练出来,以级联的方式组合所有的分类器,一个比较强的分类器就能被组成起来.

3 改进的算法及其分析

3.1 原算法分析

算法主要性质是不断减少学习过程中的训练误差,如何确定最终误差下界,对于这个问题有如下的定理[10]:

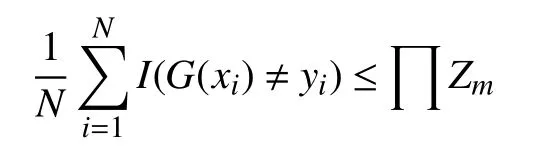
这一定理说明,在每一次迭代过程中选择合适的Gm使得Zm最小,训练的误差会下降的最快. 对于二分类问题有如下结果[11]:

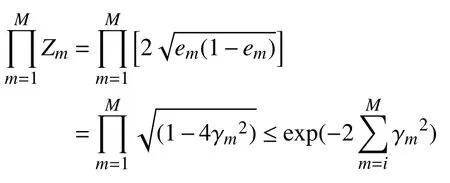
3.2 样本噪声处理

噪声数据对分类结果有很大的影响,只要在这些类中存在少量的噪声数据,就会影响这些类的分类效果. 在AdaBoost算法中只有被分类为错误样本的权值才会被扩大,在下一次分类中分类器会把重心放在权值大的样本上,然而噪声样本很难被分类正确,这类样本的权值就会变得越来越大,分类器也会趋向于过拟合,可以看出算法本身就忽略了噪声样本的存在. 另一方面噪声样本确实很难被分类正确,然而在真实环境中,噪声样本对于效果不是很好的弱分类器,噪声样本也有可能被分类正确,该样本的权值会下降,又进一步降低了被分类错误的可能,那么最终分类器的准确率必定会受影响.

为了确定样本中的噪声样本,本文提出在AdaBoost算法的一次迭代过程中会产生一些分类为错误的样本,这些样本中可以分为两部分,一类是好的样本能够在下一次分类中被分类正确,另外一类是噪声样本这类样本很难被分类正确,而且它与同一分类中的样本在某些属性上存在很大差异.

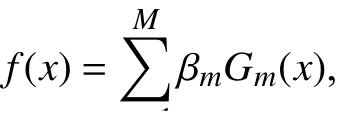
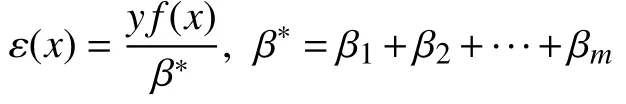
其中,β∗是规范化因子,目的使得f(x)是概论分布,保证每轮的样本权值之和为1,由于经过训练,AdaBoost在训练集上误差率已经很低了,所以他越接近于-1,可以发现被分类错误的样本的ε(x)在[-1,10]之间,如果P是噪声点,那么它的ε(x)就会越接近-1. 为了进一步确定P 样本是否是噪声数据,对于两个样本点x1,x2,使用欧几里得距离思想来定义它们之间的距离:

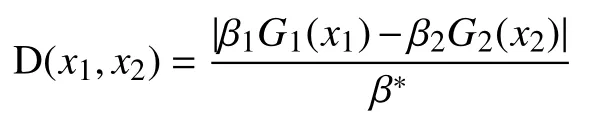
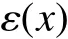
图1中折线之内为模糊地带样本,折线之外为正常样本,其中含有两个强噪声样本,本文以此来确定噪声样本并进行分类处理. 3.3节将详细讲述算法流程.

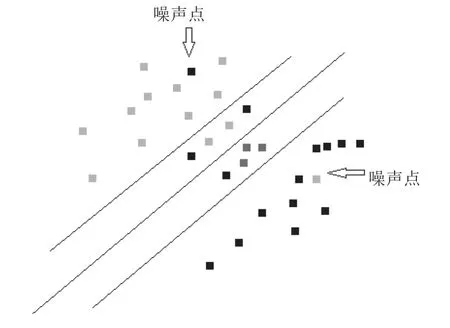
图1 噪声样本和非噪声样本分布示意图

3.3 NAdaBoost算法流程

算法2. NAdaBoost算法输入: 训练数据集(二分类); 弱学习算法(本文的弱分类器是单层决策树).输出: 最终分类器G(x).1. 用传统的AdaBoost算法得到初次分类器: .) (2. 对于每个样本计算,.3. 根据上一步的计算,将 的样本点集合记为Ususpect.4.a) 对于上述集合Ususpect根据给定的距离公式 在集合中找出与当前样本点P最临近的K个点,记为Nk(p).b) 在Nk(p)中根据分类决策规则决定P点的类别y: 根据这两个步骤得到极大可能性的噪声点集合Unoise,和不是噪声的集合Ugood=(Uall-Unoise).∑5. 分别对上述两个集合Unoise,Ugood重复进行上述步骤1分别得到分类器和,即最终的))((分类器为 .G(x)=Gn(x)x∈Unoise Gg(x)x∈Ugood

4 实验

4.1 实验方法

本文主要是针对二分类问题进行研究,因此使用著名的加州大学欧文分校提出的数据库UCI,从其中选出部分二分类数据集来进行实验. UCI数据库是行业内经常被用于数据挖掘,机器学习的标准测试数据库. 本文随机从中选取了9组数据集,如表1所示.

实验中本文所提出的算法将和传统的AdaBoost算法在相同的情况下进行对比,并且与上文提到的其他比较著名的改进算法LogitBoost,MutiboostAB,最终得出结论. 为了保证结果的准确性,本文先将各个算法在没有噪声的情况下比较分类结果,然后对各个数据集添加一定比例的噪声,再使用各个算法测试数据进行分类,比较实验结果,最终得出结论. 在本次实验中,采用的是java编程语言,结合WEKA提供的开源代码进行实验.

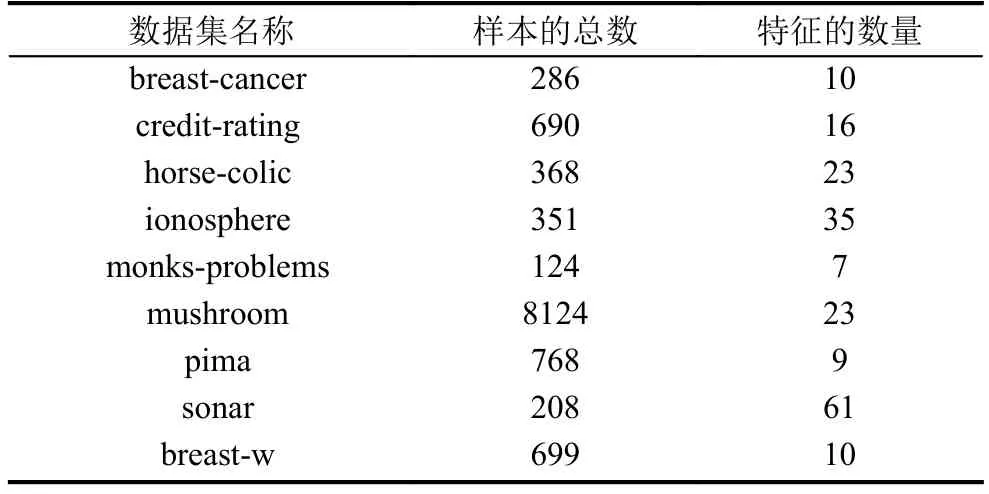
表1 数据集信息

本文算法使用的弱分类器是单层决策树,迭代次数根据原始的算法为10次(默认都是10次),k值也是根据经验取样本总数的5.6%.

4.2 本文算法与其他算法比较结果

表2至表6依次列出了在数据没有添加噪声的情况下,和添加数据数量10%的噪声,20%的噪声的情况下,各个算法的预测结果的正确率对比.

表2 没添加噪声时各个算法的预测结果对比 (单位: %)

表2的实验结果中加粗的部分是每组数据集中预测正确最高的,加下划线的是正确率最低的,因此可以清楚看出不管在有没有加噪声的情况下,本文提出的NAdaBoost算法在大多数数据集中都有很高的正确率,而且没有出现最低的正确率情况. 为了进一步体现本文算法在噪声数据干扰情况的健壮性,选择特征最多的三组数据集 (ionosphere,sonar,mushroom)分别随机添加10%,20%的噪声,测定不同噪声下各个算法的准确率,如表3至表6所示,分别记录了不同噪声下各个算法的准确率.

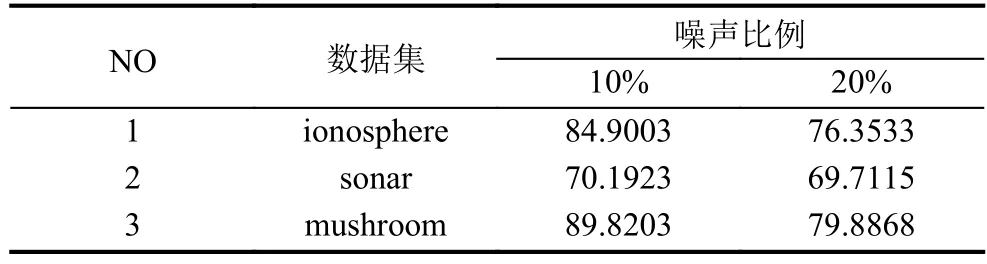
表3 NAdaBoost在不同噪声比例下的准确率 (单位: %)

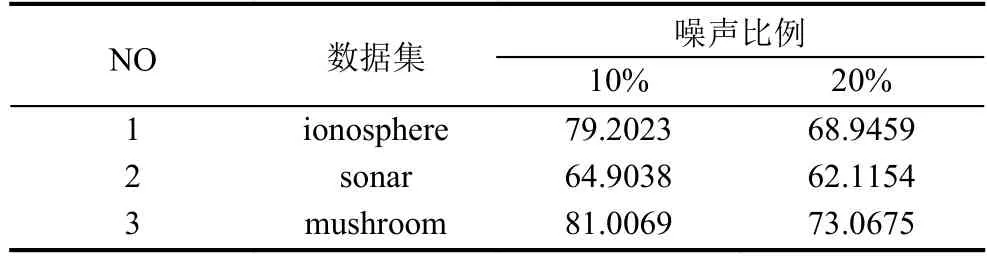
表4 LogitBoost在不同噪声比例下的准确率 (单位: %)

表5 MutiboostAB 在不同噪声比例下的准确率 (单位: %)

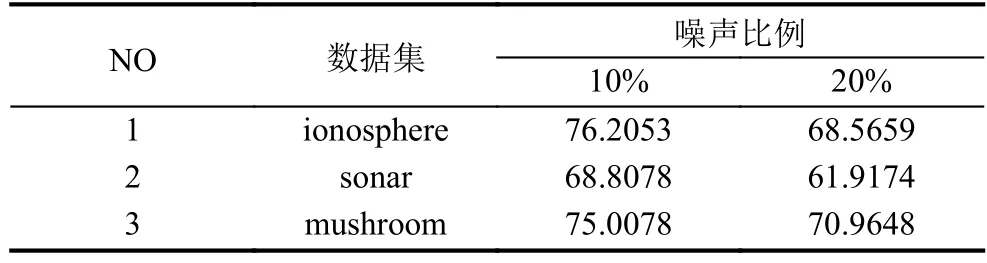
表6 AdaBoost在不同噪声比例下的准确率 (单位: %)

从表3至表6的比较可以发现NAdaBoost算法在不同的噪声比例下依然保持很高的分类准确率,并且在相同的噪声条件下,分类结果会优于其他算法. 为了便于观察分别绘制了在三个数据集上的各种算法比较的折线图,如图2所示.

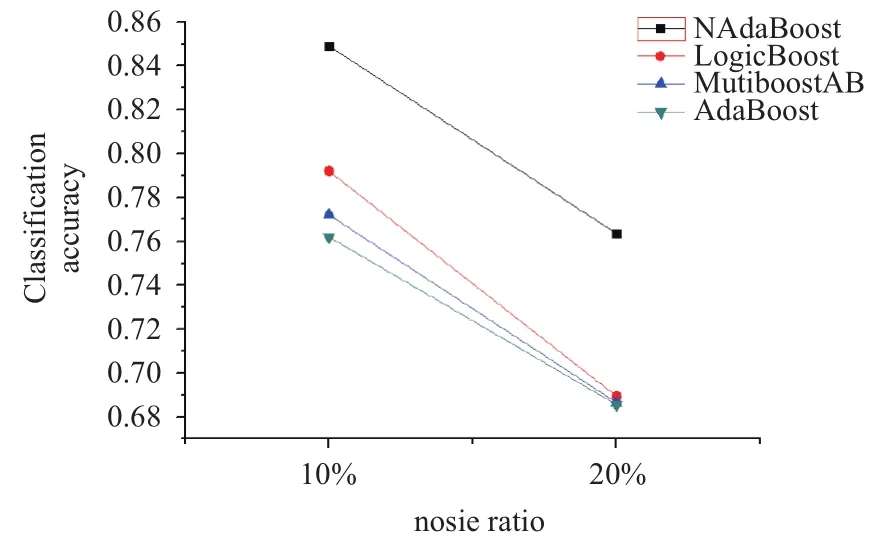
图2 ionosphere数据集下各个算法分类准确率对比

可以发现在随着噪声比例的增大各个算法的正确率都有所下降,但本文提出的NAdaBoost算法正确率下降缓慢,并且相比于其他算法依然保持最高的正确率.

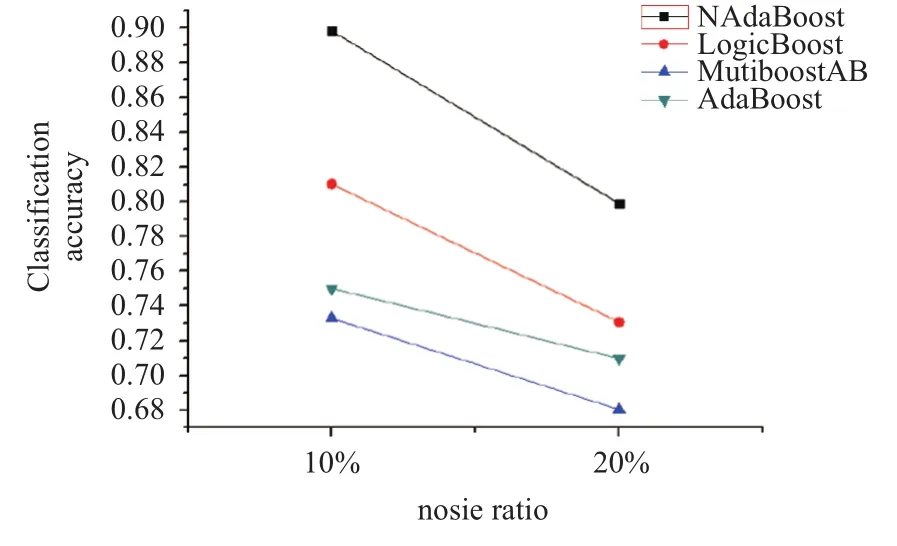
图3 mushroom数据集下各个算法分类准确率对比

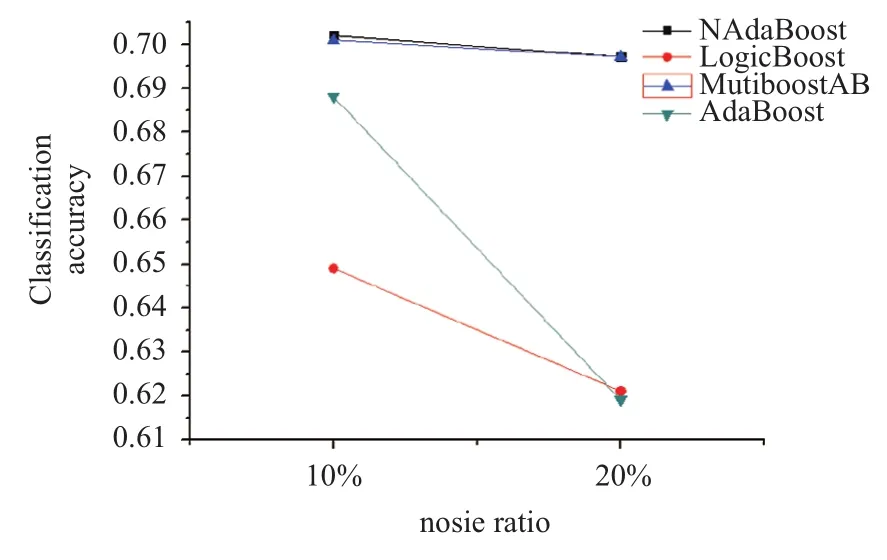
图4 sonar数据集下各个算法分类准确率对比

5 总结

本文是以AdaBoost算法为基础,针对噪声样本造成的“过拟合问题”,对临界样本在计算权值时进行抑制,对于噪声样本采用k近邻思想检测噪声样本,对重新划分的样本进行分类. 本文使用UCI数据集来实验,从多个方面来考察实验结果,表明本文提出的算法都有较好的分类准确率. 然而,在判断噪声样本时k值的选择是取样本总数的5.6%,虽然这是多次实验最终选择的取值,在大多数情况下是有效的,但也有可能会碰到极端的情况,可能样本点本身是噪声点在5.6%的范围内存在多数噪声点,算法会错误的把该样本点判断为非样本点,最终影响分类的准确率,因此k值的选择有待进一步研究. 此外本文只是针对的二分类问题,不适用于多分类问题,因为AdaBoost算法要求每个弱分类器的准确率大于1/2,但是在多分类问题中找到这种弱分类器很困难,需要从数学的角度重新创建模型,有学者提出多类指数损失函数的逐步添加模型[14],把分类器要求的准确率降到1/n(n为类别数),但这无法保证有效性,因此提升到多分类问题还需要进一步研究寻找合适的模型.

1Freund Y,Schapire RE. A decision-theoretic generalization of on-line learning and an application to boosting. Journal of Computer and System Sciences,1997,55(1): 119–139. [doi:10.1006/jcss.1997.1504]

2Freund Y,Schapire RE. Experiments with a new boosting algorithm. Proc. of the 13th International Conference on International Conference on Machine Learning. Bari,Italy.1996. 148–156.

3李航. 统计学习方法. 北京: 清华大学出版社,2012: 3.

4Schapire RE,Singer Y. BoosTexter: A boosting-based system for text categorization. Machine Learning,2000,39(2-3): 135–168.

5Viola P,Jones MJ. Robust real-time face detection. International Journal of Computer Vision,2004,57(2): 137–154.[doi: 10.1023/B:VISI.0000013087.49260.fb]

6Jiang WX. Does boosting overfit: Views from an exact solution. Technical Report 00-03,Evanston,IL: Northwestern University,2000.

7Servedio RA. Smooth boosting and learning with malicious noise. Proc. of the 14th Annual Conference on Computational Learning Theory,COLT 2001 and 5th European Conference on Computational Learning Theory. Amsterdam,The Netherlands. 2003. 473–489.

8Gao YL,Gao F. Edited AdaBoost by weighted kNN.Neurocomputing,2010,73(16-18): 3079–3088. [doi: 10.1016/j.neucom.2010.06.024]

9Webb GI. MultiBoosting: A technique for combining boosting and wagging. Machine Learning,2000,40(2):159–196. [doi: 10.1023/A:1007659514849]

10付忠良. 关于AdaBoost有效性的分析. 计算机研究与发展,2008,45(10): 1747–1755.

11Freund Y,Schapire RE. A decision-theoretic generalization of on-line learning and an application to boosting. Journal of Computer and System Sciences,1997,55(1): 119–139. [doi:10.1006/jcss.1997.1504]

12周志华. 机器学习. 北京: 清华大学出版社,2016: 1.

13Rätsch G,Onoda T,Müller KR. Regularizing AdaBoost.Proc. of the 1998 Conference on Advances in Neural Information Processing Systems II. Cambridge,MA,USA.1999. 564–570.

14胡金海,骆广琦,李应红,等. 一种基于指数损失函数的多类分类 AdaBoost算法及其应用. 航空学报,2008,29(4):811–816.

Improvement of AdaBoost Algorithm Based on Sample Noise Detection

ZHANG Zi-Xiang,CHEN You-Guang
(School of Computer Science and Software Engineering,East China Normal University,Shanghai 200333,China)

In the traditional AdaBoost algorithm,there are over-fitting problems caused by noise samples. In this paper,an improved AdaBoost algorithm based on noise detection is proposed,called NAdaBoost. According to the traditional AdaBoost algorithm,in the misclassified samples,noise samples vary widely in some attributes. NAdaBoost can,instead,determine the noise samples based on this,and then reuse the algorithm to classify the two types of samples,and ultimately achieve the purpose of improving the accuracy of classification. The experiment on the binary classification shows that the proposed algorithm has a higher classification accuracy compared with the traditional AdaBoost algorithm,as well as relative improvement of algorithms.

over-fitting; noise detection; AdaBoost algorithm; binary classification

张子祥,陈优广.基于样本噪声检测的 AdaBoost算法改进.计算机系统应用,2017,26(12):186–190. http://www.c-s-a.org.cn/1003-3254/6081.html

2017-03-03; 修改时间: 2017-03-20; 采用时间: 2017-03-29