基于FPGA及分布式算法滤波器

周龙，王红玲，崔新莹，黄琳华

（哈尔滨理工大学应用科学学院电子科学与技术，黑龙江哈尔滨150080）

基于FPGA及分布式算法滤波器

周龙，王红玲，崔新莹，黄琳华

（哈尔滨理工大学应用科学学院电子科学与技术，黑龙江哈尔滨150080）

文中基于分布式算法实现FIR数字滤波器的设计方案。该方案分为3部分，首先是利用Matlab软件产生需要的数据；使用FDATool工具包生成滤波算法所需要的系数；完成ROM查找表中数据的计算。第二部分是采用分布式算法设计基于FPGA的实现结构，完全避免了乘法运算，资源优化性高；第三部分通过对FPGA的滤波器设计方案进行仿真验证，并与使用Matlab模拟滤波算法产生的波形进行比较，两者能够达到几乎一致，得出电路设计合理，滤波效果达标的结论。

FIR；FPGA；分布式；并行结构

滤波器是一种选频设备，可以选取所需的信号频率，抑制不需要的信号频率。根据选频范围可分为4种基本类型:低通滤波器、高通滤波器、带通滤波器、带阻滤波器。低通滤波器的选频范围是低于某一频率的信号不受衰减，而高于该频率的信号受到大幅衰减；高通滤波器选频范围与低通滤波器相反；带通滤波器的选频范围是在某两个频率之间信号可以正常通过，而其余频率的信号衰减；带阻滤波器与带通滤波器相反[1-2]。

1 设计概述

滤波器的应用领域非常广泛，从民用设备到军用设施，滤波器都是必不可少的重要工具。实现滤波器的方案有很多种，但是从信号稳定性及不失真的角度看，FIR数字滤波器具有明显优势，能够避免模拟滤波器电压漂移、温度漂移、噪声等问题，同时FIR滤波器没有反馈回路，所以稳定，也可以保证精确的线性相位。最常见的数字滤波器都是线性时不变系统，其数学表达形式是一个卷积式，卷积过程如（1）所示。

本设计是基于以上的算法实现一种改进算法的FIR数字滤波器。其技术指标是:截止频率为10 800 Hz、采样频率为48 000 Hz、带宽3 dB、16阶的FIR低通数字滤波器。FIR数字滤波器可以通过软件或者硬件两种方式实现。软件的方式是在通用计算机上运行滤波软件，软件可以使用已经被开发出来的工具包进行设计，也可以自行编程完成，但是软件实现的速度慢。硬件实现的方式可以加速计算。本文针对基于FPGA的硬件方案进行研发设计，并与使用Matlab工具包进行滤波的仿真效果进行对比。

2 Matlab工具包

FDATool是Matlab提供的一种关于滤波器设计的工具包。在FDATool的界面上设置滤波器参数如图1所示，依次设置为:FIR低通滤波器、窗函数法设计、窗口类型是Kaiser、16阶、采样频率48 000 Hz、截止频率10 800 Hz。

图1 FDATool界面参数设置

如图1可见，在横坐标超过10 kHz的位置，信号振幅开始大幅衰减，产生滤波效果；在10 kHz之前，信号振幅较平稳，维持在上下波动不超过3 dB的范围内。本设计利用窗函数法产生FIR滤波器系数，对FIR滤波器而言，冲击响应就是滤波系数，因此可以从时域出发，选取一个理想滤波器，截取有限长的一段单位冲击响应作为系数，冲击响应的长度就是滤波器的阶数。由于冲击响应对称，因此该方法生成的系数具有对称性。针对本设计16阶的滤波器，窗函数法生成的系数导出，如图2所示。

为了完成后续对滤波器的仿真测试，需要先生成带干扰的数据，作为滤波器的输入数据，进行滤波处理，本设计使用2 000 Hz的正弦波上叠加20 000 Hz的余弦波，得到的波形如图3所示。

图2 窗函数法生成系数

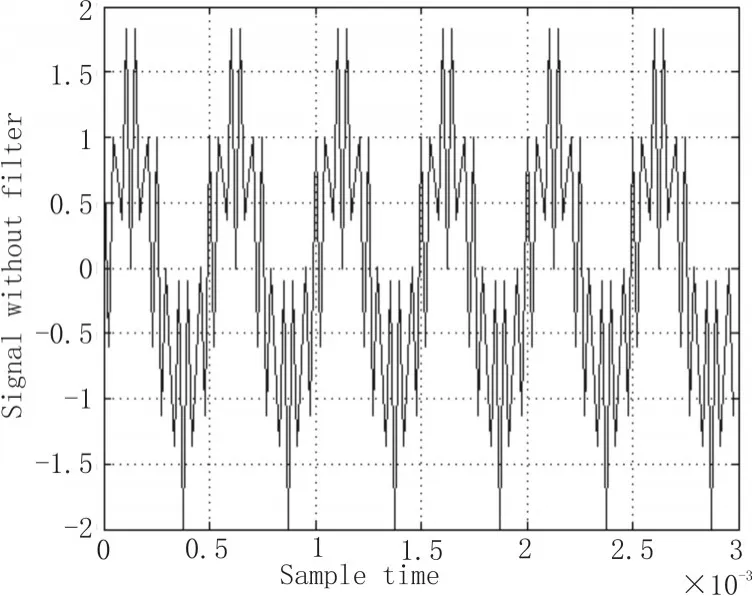
图3 带干扰波形

如图3所示，叠加波形的数据范围在-2～+2之间，将数据打印出来，如图4所示。

图4 干扰后的数据

可见所成的数据均为浮点数，在硬件系统中对浮点数进行运算处理是比较困难的，因此，本设计考虑采用Q格式转换的方法，对浮点数据进行转化。Q格式转化的思想是先对浮点数据进行扩大，扩大成整数，用整数进行运算，结果再按照相应的倍数缩减。Qn表示小数点后有n位数，将小数点右移n位即得到扩大后的浮点数。如表1所示，列出几种常用Qn形式及其适用数值范围与精度。根据所需要扩大数据的范围选择Qn类型。同时，为了方便计算，本设计先将数据转化为无符号数据计算，采取的方法是令输出数据先加2，再使用Qn格式转化，相当于将上述波形整体向上移动两个单位，使所有数据全部在正数范围内表示。对照本设计采用的带干扰数据，可以确定在Q13格式的范围内，因此，对本设计的干扰数据进行Q13格式的扩大。

表1 Qn格式

3 FPGA硬件设计

分布式算法:根据上文的卷积式（1）可知，滤波算法实际上就是计算乘累加的过程，在FPGA设计中，分布式算法是一种实现乘累加的重要解决方案，能够显著节省硬件资源，提升运算速度。本设计即是采用分布式算法实现FIR滤波器[3-5]。

等式（2）代表L阶FIR滤波器的输出。L是滤波器系数h（k）的阶数，x（n）代表输入的时间序列。

假设h[n]均为已知常数，x（n）代表输入，x（n-k）代表延迟了k个周期后的数据，在硬件中即代表输入在寄存器中传递了k级，等式（2）可是被重写为如下:

当输入数据是二进制，x[n]可以被表示成式（4），其中xb(n)是x[n]的第b位，B是输入位宽:

将式（4）待入式（3）并进一步化简:

上式即得出了L个样本依次输入，通过系数c[n]每一次和x[n]中的一位做与运算获得部分乘积。在FPGA中，与操作和加法器可以由由查找表代替来得到部分积。将二进制数x[n]与系数c[n]相乘的可能性全部计算出来存储到查找表中。这样，就可以通过x[n]作为二进制的地址来查找每一次乘积的结果。再将得到的结果向左移位来完成与2＾b相乘。每一个输入的每一位都进行以上操作，最后，将所有的结果累加即可获得输出值。这里要说明的是，由于硬件系统每个周期只能输入一个数据，因此，在小于阶数L个周期内，乘积累加和的结果并不准确，假设本周期输入第3个数据，阶数是16，那么:

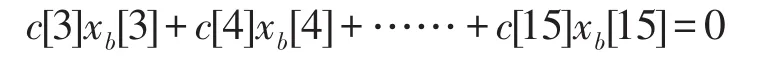
可见，只有当数据多余阶数个时，才会有完整的计算结果。

FPGA设计结构:根据以上对于分布式算法的介绍，采用FPGA的并行方式实现，可以加速计算。本设计完成16阶FIR数字滤波。设计结构图如图5所示。

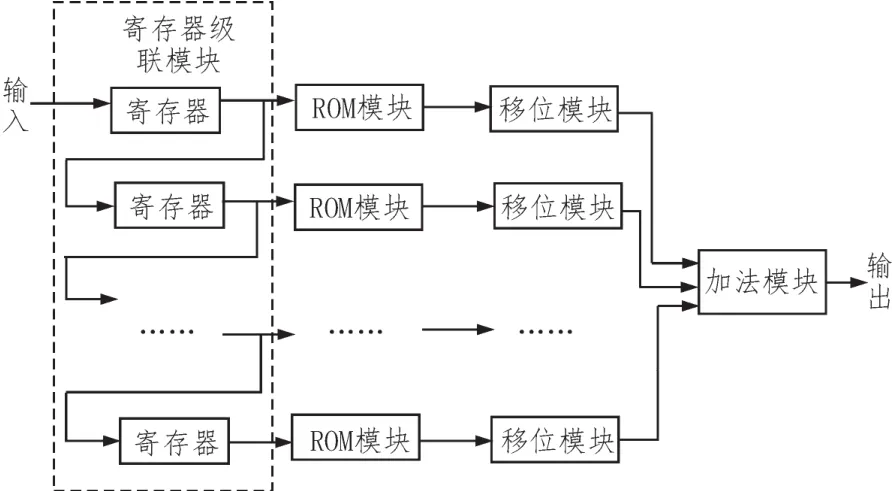
图5 FIR滤波器结构图

第一个级联模块，是将16个输入数据一级一级向下传递并存储在寄存器中，一个N阶的滤波器，级联模块应该保留N个输入数据。因此，在前16个时钟周期，寄存器级联模块中没有填满数据，输出结果在16个时钟周期之后有效。

ROM模块输出的结果作为移位模块的输入数据，在数字电路中，向左移一位代表乘以2，在分布式算法中，每一个ROM的输出结果都需要乘以2^b（对于任意一个ROM，b的值是固定的），如果使用乘法器实现这步计算，是需要占用很多FPGA内部资源的，因此，将乘法计算转化成移位操作，节省了资源也简化了计算。移位模块的输出作为加法模块的输入，加法模块将所有的计算结果进行累加，即得到最终的滤波结果。

4 仿真与验证

硬件仿真是使用ISE自带仿真工具ISIM进行，将Matlab产生的带干扰的数据作为输入激励，将Matlab中计算的查找表数据存入ROM，仿真得到的结果数据存入文本文件中，Matlab读取并打印出波形，如图6中标识“Filter using FPGA”的波形图所示。在本设计中配合使用了Matlab软件用来产生数据及打印波形，Matlab还可以用来完成仿真设计。本设计即使用了未经改进的滤波算法在Matlab上进行了仿真验证，与FPGA模块处理的波形做滤波效果的比对，如图6中标志的“Filter using Matlab”即是直接使用Matlab实现[6-9]。

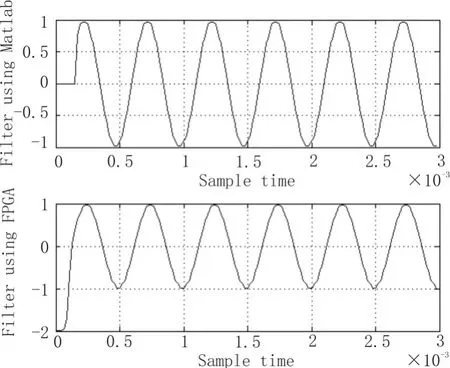
图6 Matlab实现与FPGA实现的滤波对比图

由上图可见，在波形起始处，由于数据小于滤波器设定的阶数，计算的结果是不准确的，当输入数据量达到设定的滤波阶数后，两种方法滤波处理后的波形完全一致，说明FPGA模块实现的分布式算法的滤波器与软件使用卷积方法实现的滤波器在滤波效果上没有差别，但是硬件模块速度更快，而且分布式算法能够节省资源[10-15]。

5 结束语

本文完整地讨论了基于FPGA的FIR滤波器的设计，并对其中涉及关键问题进行了详细的讨论。针对优化资源和结构，采用了分布式的解决方法。使用该设计方案在简化算法的同时，提升了滤波的速度与性能，具有很高的推广价值。

[1]梁丽娟，安兰珠.利用MATLAB实现FIR数字滤波器设计[J].中国科技信息，2012（10）:137.

[2]何蕴良，耿淑琴，汪金辉.基于Verilog的FIR数字滤波器设计与仿真[J].现代电子技术，2016，39（10）：1-4.

[3]郭广浩，刘志哲，孟庆龙，等.多级并行流水FIR数字滤波器的设计与验证[J].现代电子技术，2015（1）:69-72.

[4]余琳，黄光明.基于FPGA的FIR滤波器的性能研究[J].电子设计工程，2011（9）:125-128.

[5]高耀鸿.基于FPGA的FIR低通滤波器[D].长沙：湖南大学，2012.

[6]曹振吉，何敏.基于FPGA和Matlab的FIR数字滤波器[J].现代电子技术，2015（19）:98-101.

[7]赵秀鸟，仲佳嘉.一种FIR数字滤波器的快速算法及DSP实现[J].数字技术与应用，2011（6）:131-132.

[8]余丹，孙文.Matlab软件设计应用之FIR数字滤波器[J].山东工业技术，2015（10）:140-140.

[9]付正，郑维智，江远志.基于FPGA的并行FIR数字滤波器硬件实现及优化[J].食品科学技术学报，2010，28（5）:69-74.

[10]王香，张莉莉.基于FPGA的16阶FIR数字滤波器的设计[J].电子世界，2013（16）:148-149.

[11]栾军，王俊，袁运能.基于fpga的高速fir数字滤波器:CN，CN 102355232 A[P].2012.

[12]郑争兵.基于DSP Builder的FIR数字滤波器设计与仿真[J].陕西理工学院学报:自然科学版，2013，29（2）:34-38.

[13]赵颖，刘祖深，李胜寅.基于MATLAB的FIR数字滤波器的方法设计[J].国外电子测量技术，2012，31（10）:35-37.

[14]刘庆良，卢荣军，李建清.FIR数字滤波器的FPGA实现研究[J].电子设计工程，2010，18（3）:59-61.

[15]赵涛，蒋媛.基于Matlab的FIR数字滤波器的设计[J].科技信息，2010（18）：386-387.

Filter based on FPGA and distributed algorithm

ZHOU Long，WANG Hong-ling，CUI Xin-ying，HUANG Lin-hua
（School of Applied Science，Electronic Science and Technology，Harbin University of Science and Technology，Harbin150080，China）

The design scheme of FIR digital filter based on distributed algorithm is implemented in this paper.The scheme is divided into three parts，the first is the use of Matlab software to generate the required data；the use of the FDATool toolkit to generate the coefficients of the filter algorithm；complete the calculation of the data in the ROM lookup table.The second part is the design and implementation of distributed algorithm based on the FPGA structure，completely avoid the multiplication，resource optimization；the third part is simulated through the design of FPGA filter，and simulation and filtering algorithm using Matlab waveform comparison，both can achieve almost the same，the circuit design is reasonable，the filtering effect of the standard conclusion.

FIR；FPGA；distributed algorithm；parallel structure

TN492

A

1674-6236（2017）23-0139-04

2016-09-21稿件编号：201609189

周龙（1993—），男，山西朔州人。研究方向：电子科学与技术。