长江经济带区域创新系统投入与产出效率研究

李 邃，万秉烛

（安徽财经大学 统计与应用数学学院，安徽 蚌埠 233030）

0 引言

长江流域孕育了发达的长江经济带。长江经济带是整个长江流域最为发达的区域，也是中国除了沿海开放地区之外，经济密度最大的经济地带，其对中国经济的发展具有重要的战略意义。当前，随着投资效率的边际递减，国际环境驳杂莫测，我国的经济增速逐步减缓，经济发展正处于转型期，即我国务必要完成经济增长由要素驱动型向创新驱动型的改变。而“实现创新驱动产业转型升级”正是长江经济带建设的目标之一，因此对于长江经济带的区域创新的研究具有较强的实际意义。

区域创新系统是在2000年由Cooke率先提出的一个概念，他认为区域创新系统是一种支持并产生创新的一种综合体系：由在地理上相互分工和关联的生产企业、研究机构和高等教育机构等构成的区域性组织体系[1]。黄鲁成[2]就区域创新系统的研究实质作了相关论述，探究了区域创新系统的规律。目前，学者们针对区域创新体系的研究主要集中在概念界定、效率评价（多采用DEA进行分析）和建设模式研究方向：概念界定方面的研究结果表明，区域创新系统的概念主要是由创新体系与区域科学结合而提出的跨学科概念[3]；效率评价与建设模式方面的研究结果表明，目前我国整体区域创新效率较低，各地区创新效率差异较大，主要原因是在于纯技术效率低下[4]。对于区域创新系统的研究，可以分析出创新投入要素在区域内能否有效配置，是研究区域创新系统科学发展的强有力工具，而纵观目前的研究成果，多为直接研究区域研究投入与产出的效率，并未先行分析投入与产出间的相关性关系。

基于此，本文将通过典型相关分析，确认长江经济带区域创新系统的投入与产出关系的存在，并在此基础上，通过超效率DEA模型测度长江经济带11个省市的效率评价值，为提升长江经济带的产业创新系统效能提供理论依据。

1 研究方法

1.1 典型相关分析[5]的基本理论及方法[6]

为了研究x、y之间的相关关系，考虑它们的线性组合：

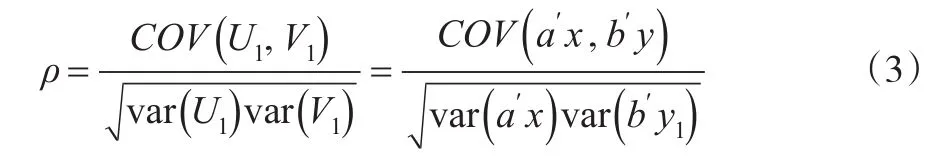
取标准化的随机变量U1和V1，规定U1和V1的反差为1，即：

因此：

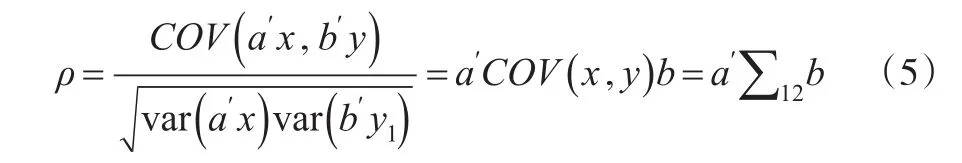
于是问题转化为满足式（4）的约束下，求a∈Rp、b∈Rq，使式（5）最大。

这一问题等价于求a∈Rp、b∈Rq，使G达到最大：

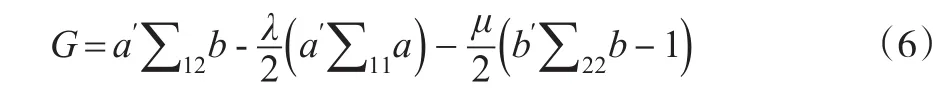
其中，λ、μ是拉格朗日乘数因子。

对G的两边分别求关于a及b的偏导数并令其为0，得到方程组：

因此，解方程组：

取第i个最大的特征根 λi，可求得ai和bi，进而可求得第i对典型变量

可用Bartlett提出的大样本χ2检验进行典型相关的显著性检验，构造统计量：

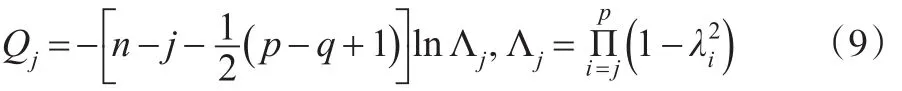
统计量Qj服从自由度为 （p -j+1）（q- j+1） 的 χ2分布。

1.2 超效率DEA模型

1.2.1 超效率DEA模型的演变

数据包络分析方法是由Charnes和Cooper等（1978）[7]提出的基于规模报酬不变模型（CCR），它使用数学规划模型对决策单元进行效率评价，通过计算效率值来评价决策单元间的相对有效性，当效率值为1时即为有效。传统DEA模型计算出的效率值限制在[0,1]的范围内，会导致在出现较多的有效单元情况下，无法对这些有效单元进行对比。为弥补传统DEA模型的不足，P Andersen和NC Petersen（1993）[8]提出超效率DEA模型，计算出的效率值可以超过1，以便对有效单元进行评价。

1.2.2 超效率DEA模型体系[9]

假设有n个决策单元，它们的投入和产出数据分别为（xj，yj）（j=1，2，…，n），对于第 j0（ ）1≤j0≤n 个决策单元，超效率DEA模型计算第 j0个决策单元超效率值的评价表达

式为：

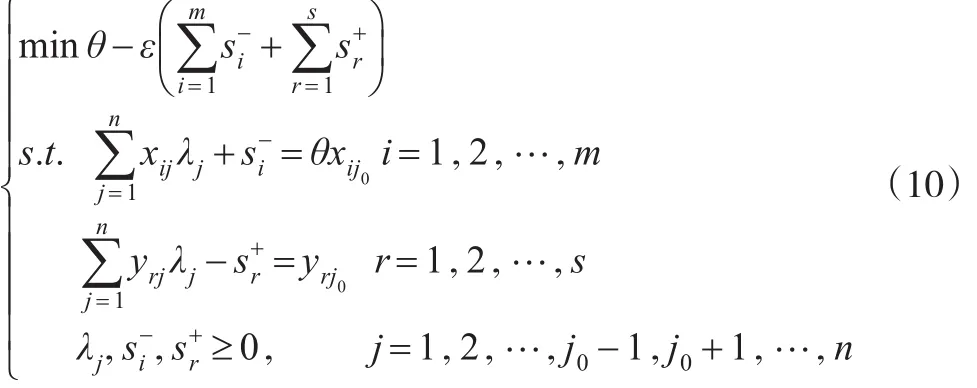
其中，θ为第 j0个决策单元的超效率值；ε为非阿基米德无穷小量，n为决策单元（DMU）个数，每个决策单元均包括m个输入变量和s个输出变量分别为输入和输出的松弛变量；xij表示第 j个决策单元在第i个输入指标上的值；yrj表示第 j个决策单元在第r个输出指标上的值；λj为输入输出指标的权重系数为未知参量，可由模型求解。

2 指标选取和数据说明

2.1 投入与产出指标

区域产业创新是一个创新资源从投入到产出的转化过程，为此本文从投入—产出的角度分别选取如下指标体系（如表1所示）。

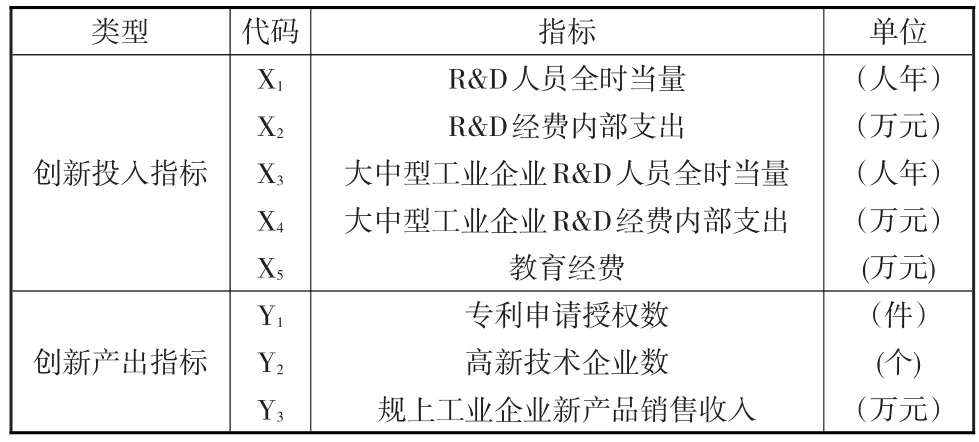
表1 投入—产出指标体系

2.2 数据说明

本文以长江经济带11个省市为研究对象。由于区域产业创新系统的投入与产出之间具有一定的时滞效应，因此需要考虑创新投入—科技成果产出—经济转化指标间的时间差[10]。参照于明洁[11]的做法，在创新的投入与产出平均转化时间为4.3的基础上，选取了4年的时滞，故本文选取了2010年的产业创新投入数据和2014年的产业创新产出数据进行分析。数据来源于相应年份的《中国科技统计年鉴》和《中国统计年鉴》。原始数据如下页表2所示。

3 实证分析

3.1 区域产业创新系统投入与产出典型相关分析

3.1.1 典型相关系数与检验

对于原始数据，使用Stata软件实现典型相关分析。由于原始数据各指标的量纲不同，数据大小差别过大，为消除量纲的影响，采用标准化的典型系数。共提取出了3对典型相关变量，得到的典型相关系数为：λ1=0.9986；λ2=0.9260；λ3=0.8804。三个典型相关系数都比较高，表明典型变量之间均高度相关；三对典型相关系数均通过了似然比法检验（如表3所示），检验1-3时，其零假设为所有典型相关系数都为零；检验时2-3时,其零假设为典型相关系数λ2、λ3都为零，依此类推，表明三个典型相关系数在0.05的显著性水平上都是显著的；检验1-3结果即为典型根的检验，典型根检验在0.05的显著性水平上是显著的，同时其他检验系数表明建立的模型是显著的（如表4所示），可以用创新投入组变量来解释创新产出组变量；得到的典型相关模型如表5所示。

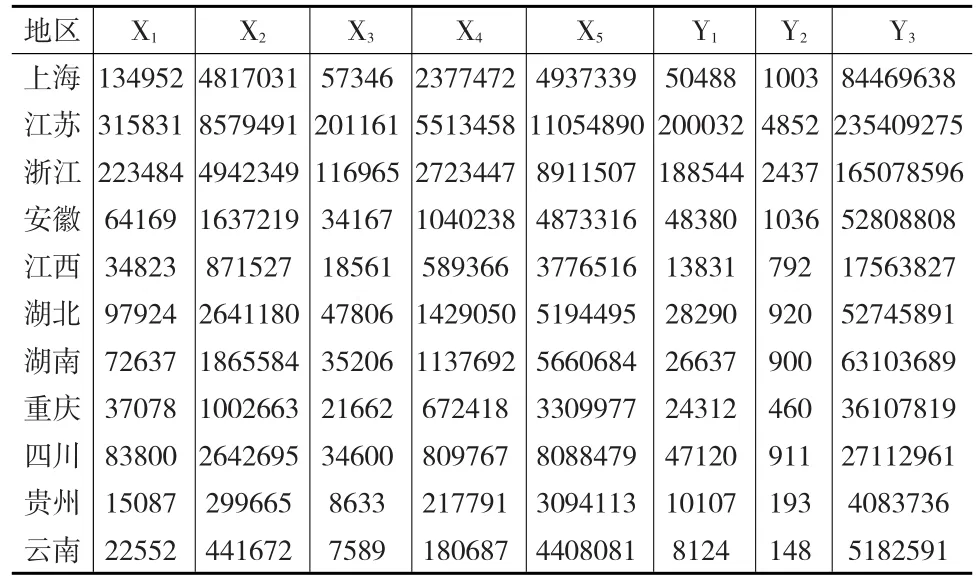
表2 长江经济带区域产业创新投入（2010年）与产出（2014年）数据

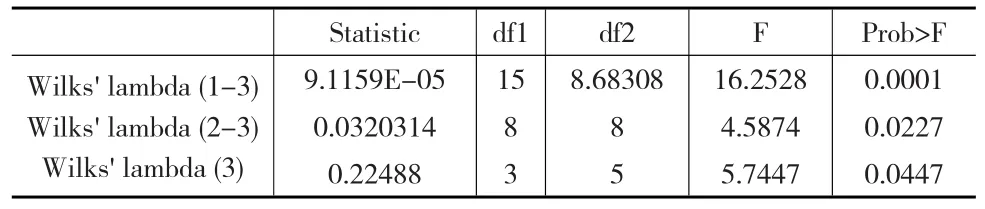
表3 典型相关系数的检验

表4 典型根的检验

表5 典型相关系数模型

从表5的结果可以看出：

（1）第一对典型变量（U1，V1），（λ1=0.9986）中，U1为创新投入组各指标的线性组合，其中X4（大中型工业企业R&D经费内部支出）占有较大的典型载荷，占据主导作用；V1为创新产出组各指标的线性组合，其中Y2（高新技术企业数）和Y3（规上工业企业新产品销售收入）占有较大的典型载荷，占据主导作用。结合指标实际意义，U1反映了创新的财力资源的投入，V1反映了区域内企业的直接产出，即表明创新的财力资源的投入对区域内企业的直接产出有重要的促进作用。

（2）第二对典型变量（U2，V2），（λ2=0.9260）中，U2为创新投入组各指标的线性组合，其中X4（大中型工业企业R&D经费内部支出）占有较大的典型载荷，占据主导作用；V2为创新产出组各指标的线性组合，其中Y1（专利申请授权数）占有较大的典型载荷，占据主导作用。结合指标实际意义，表明工业企业R&D经费内部支出越多，对区域内的专利数产出有一定的反作用。原因可能是因为长江经济带以产业为先驱，导致创新资金的投入过多流入到企业生产创新环节，而非核心专利研发中去，今后需注重在企业核心专利研发方向的投入。

（3）第三对典型变量（U3，V3），（λ3=0.8804）中，U3为创新投入组各指标的线性组合，其中X1（R&D人员全时当量）和X3（大中型工业企业R&D人员全时当量）占有较大的典型载荷，占据主导作用；V3为创新产出组各指标的线性组合，其中Y3（规上工业企业新产品销售收入）占有较大的典型载荷，占据主导作用。结合指标实际意义，创新的人力资源的投入对区域内企业的直接产出有重要的促进作用；然而企业对创新人力资源的过度投入对区域内企业的新产品销售有一定反作用，即研发人员的过度投入，导致没有充足人力资源去开拓市场，对产品的销售起反作用。

3.1.2 典型载荷与交叉典型载荷

如表6、表7所示的典型载荷与交叉典型载荷，X1至X5都与创新投入组第一典型变量高度相关，说明所选取的创新投入指标很好地诠释了创新投入情况。同时X1至X5都与创新产出组高度相关，说明创新投入是影响创新产出的主要因素。

Y1至Y3都与创新投入组第一典型变量高度相关，说明所选取的创新产出指标很好地诠释了创新产出情况。同时Y1至Y3都与创新投入组高度相关，同样说明创新产出受创新投入的影响。

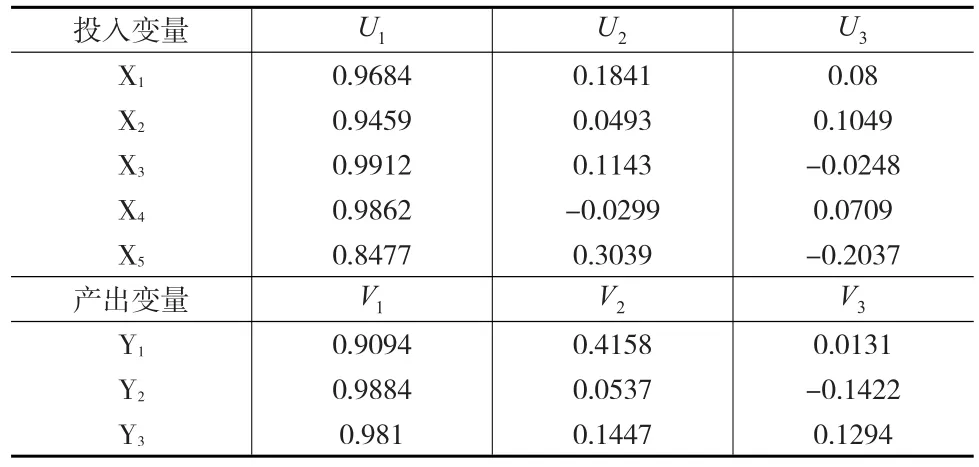
表6 典型载荷

表7 交叉典型载荷

3.1.3 典型冗余分析

典型冗余分析主要揭示变量的解释能力。典型冗余分析结果如表8所示。

表8 典型冗余分析

两组变量的第一典型冗余分别达到94.27%和100%；第二典型冗余分别达到了93.32%和98.52%，表明三对变量都很好地预测了对应的那组变量，同时也能被对应的那组变量所解释。第一对的典型相关系数的平方达到了0.9972，具有极高的解释百分比，说明创新投入与产出间具有显著相关性。

3.2 区域产业创新投入产出效率测度

通过对长江经济带区域产业创新系统投入与产出间的典型相关分析，可以看出长江经济带区域产业创新系统投入指标与产出指标间具有显著的相关性，因此可以根据选取的指标对其创新投入产出效率进行分析。通过Matlab7.0分析原始数据，将11个省市作为决策单元，得到其创新投入产出效率结果，如表9所示。

表9 长江经济带产业创新投入产出效率评价

总体而言，长江经济带11个省市创新投入产出效率评价值θ低于0.8的只有云南，这表明长江经济带总体产业创新投入转化为创新产出的过程是有效的。另可将其地区分为三个类型：相对高产业创新投入产出效率地区（江西、浙江、四川、重庆、湖南、安徽、江苏，其θ＞1）；中等产业创新投入产出效率地区（上海、贵州、湖北，其0.8＜θ≤1）；相对低产业创新投入产出效率地区（云南，其θ≤0.8）。

通过超效率DEA方法对长江经济带的区域产业创新投入产出效率的测算，发现长江经济带总体创新投入转化为创新产出的过程是有效的。三类不同的创新投入产出效率地区测度分析结果如下：

（1）相对高产业创新投入产出效率地区（江西、浙江、四川、重庆、湖南、安徽、江苏）。这些地区都存在一定数量的工业企业，工业带动产业创新，伴随而来的是较高的产业创新投入产出效率。

（2）中等产业创新投入产出效率地区（上海、贵州、湖北）。这三个地区中上海是金融中心，主要为文化产业带动的产业创新，相较工业企业较多的地区，产业创新效率略有不足，但其整体发展水平较高，致使其产业创新效率能够健康可持续的保持，这种模式也值得借鉴和推广；而湖北作为老牌工业地区，产业创新效率不够明显，在今后的发展中需向产业创新方面靠拢；贵州则是作为一个逐步提升产业创新投入产出效率的典范，需保持这种发展态势。

（3）相对低产业创新投入产出效率地区（云南）。云南作为一个地理位置偏远与经济欠发达地区，产业创新起点较低，需要长江经济带在产业创新协调发展过程中对其倾斜相关资源与政策，助力长江经济带产业创新协调发展。

4 结论

通过典型相关分析法，对长江经济带11个省市的区域产业创新系统投入与产出关系进行研究，结果表明区域产业创新系统投入与产出间具有显著的相关性，变量中多数系数也为正号，表明长江经济带区域创新系统投入对产出有一定的促进作用。同时，通过对长江经济带的区域产业创新投入产出效率的测算，也发现长江经济带总体创新投入转化为创新产出的过程是有效的，但仍存在地区发展不平衡的现象。对于此，需加强长江经济带各区域间的产业联动，带动区域协调发展：在未来发展过程中，需提升高效率地区地区的产业创新效率的辐射带动能力，开创长江经济带协同产业创新发展的新格局；同时对低效率地区，倾斜相关资源与政策，助力长江经济带产业创新协调发展。

[1]官建成,何颖.基于DEA方法的区域创新系统评价[J].科学学研究,2005,23（2）.

[2]黄鲁成.关于区域创新系统研究内容的探讨[J].科研管理,2000,21（2）.

[3]毛艳华.区域创新系统的内涵及其政策含义[J].经济学家,2007,2（2）.

[4]白俊红,江可申,李婧.中国区域创新系统综合评价及分析[J].管理评论,2009,21（9）.

[5]何晓群.多元统计分析[M]北京:中国人民大学出版社,2015.

[6]张淑辉,陈建成,张立中,张新伟.农业经济增长及其影响因素的典型相关分析——以山西为例[J].经济问题,2012,（5）.

[7]Charnes A,Cooper W W,Rhodes E.Measuring the Efficiency of Deci⁃sion Making Units[J].European Journal of Operational Research,1978,（2）.

[8]Andersen P,Petersen N C.A Procedure for Ranking Efficient Units in Data Envelopment Analysis[J].Management Science,1993,（10）.

[9]刘展,屈聪.MATLAB在超效率DEA模型中的应用[J].经济研究导刊,2014,（3）.

[10]李邃,江可申,郑兵云.基于链式关联网络的区域创新效率研究——以江苏为研究对象[J].科学学与科学技术管理,2011,32（11）.

[11]于明洁,郭鹏.基于典型相关分析的区域创新系统投入与产出关系研究[J].科学学与科学技术管理,2012,33（6）.