基于投影寻踪模型的网评评委综合素质评价

梁 薇

（江西警察学院 刑科系，南昌 330103）

0 引言

当今，我国各级教育主管部门为了提高大学生的综合素质，组织开展全国性或区域性的大学生综合素质竞赛，如全国大学生“挑战杯”竞赛、大学生数学建模竞赛、大学生创新创业竞赛等。各类竞赛层出不穷，为了确保竞赛评比结果的公平和公正，有效地控制评卷过程中人为误差，提高竞赛结果的公信力。因此，将互联网技术应用到竞赛评阅当中。选择网络阅卷已成为提高整个竞赛管理效率中的一个至关重要环节。

本文以某省教育主管部门某年组织的高校研究生数学建模竞赛网评评委的实际数据为样本，在提出评价指标体系基础上，利用客观赋权法中探索性数据分析—投影寻踪法，并结合遗传算法建立了遗传—投影寻踪评价模型，运用该模型对这次研究生数学建模竞赛的网评评委综合素质进行评价，以期达到提高网络阅卷质量和竞赛公信力的目的。

1 遗传算法的投影寻踪模型综合评价模型

为了更准确地评价网评评委综合素质，考虑建立一个涵盖各个指标的综合评价模型，最常用的方法是采用主成分法。由于评价网评评委工作的优劣没有一个明确的标准，所以只能建立无监督的评价模型。同时考虑到一个优良评价体系应能将不同表现的群体尽可能的区分开，才能达到评价的目的，因此本文采用投影寻踪法以聚类的方式建立一个能尽可能区分不同基本素质评委的综合评价模型。

投影寻踪是用来分析和处理高维数据，尤其是非正态、非线性的高维数据的一类统计方法。基本思想是把高维数据通过某种组合投影到低维的子空间上，并通过极小化某个投影指标，寻找出能反映高维数据结构或特征的投影，在低维空间上对数据结构进行分析，已达到研究和分析高维数据的目的。

遗传算法是解决函数优化问题的数据挖掘方法，智能算法的一种，是通过计算机编码实现生物学进化过程中的复制、交叉、变异、线性、倒位等遗传过程，实现系统设计、函数优化等复杂过程。计算的结果是一种通过模拟自然进化过程搜索最优解的方法。

用遗传算法的投影寻踪技术建立投影寻踪聚类模型步骤：设第i个样本第 j个指标为2，…,m;），其中n为样本个数，m为指标个数。

（1）将样本指标数据归一化处理。由于各指标的量纲不尽相同或数值范围相差较大，因此，在建模之前对数据进行归一化处理为：

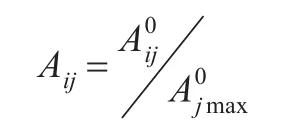
（2）建立数据的线性投影。所谓投影实质上就是从不同的角度去观察数据，寻找最能充分发掘数据特征的作为最优投影，方可在单位超球面中随机抽取若干个初始投影方向a（a1， a2，…，am），计算投影指标的大小，根据指标选大的原则，最后确定最大指标对应的解为最优投影方向。

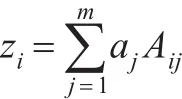
（3）寻找目标函数。综合投影指标值时，要求投影值zi的散布特征应为：局部投影点尽可能密集，最好凝聚成若干点团；而在整体上投影点团之间尽可能散开，故可将目标函数Q（a）定义为类间距离s（a）与类内密度d（a）的乘积，即：

Q（a）=s（a ）⋅d（a）

类间距离用样本序列的投影特征值方差计算：

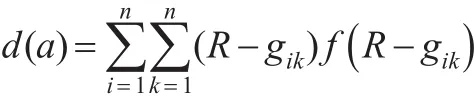
（4）优化投影方向。由上述分析可知，当Q（a）取得最大值时所对应的投影方向就是所要寻找的最优方向。因此，寻找最优方向的问题可转化为下列优化问题：

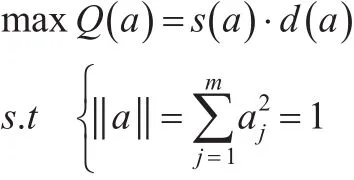
在满足约束条件的情况下，求出Q（a）的最大值，同时也就找到了最优投影方向。由于这是一个复杂非线性优化问题，可采用遗传算法进行优化。

（5）综合评价聚类分析。根据最优投影方向，便可计算反映各评价指标的综合信息的投影特征值Zi，以Zi的差异水平对样本群进行聚类分析并进行综合评价。

2 遗传算法的投影寻踪模型在网评评委综合素质评价中的应用

2.1 数据来源与处理

本文采用某省教育厅组织的一次研究生数学建模竞赛的数据。该比赛共有五个题目，共聘请了196名网评评委。每个题目根据提交论文（或项目）的多少分配网评评委，最多的D题共有69名网评评委，最少的A题共有14名网评评委。每篇论文至少四位评委评阅，每个评委评阅八至十篇不等。现根据各网评评委在网评阶段的评分结果以及最终论文的成绩，对各网评评委综合素质进行评价。

2.2 指标体系构建

运用投影寻踪模型对网评评委的综合素质作评价，首要条件是构建合理的度量网评评委综合素质的指标体系。由于网评评委对参赛论文（或项目）仅仅是根据自身的知识和经验等因素综合判断给出一个分值，如何使用一个具体分值来构建评价指标体系，成为本文的重点之一。为此，本文在对各类竞赛进行定性分析基础上，遵循全面性和代表性的原则，将对每个网评评委的评分结果从不同角度进行分析，通过相关转换提取了宽严度、离散度、可靠度、有效度和准确度五个指标，以五个指标构建网评评委综合素质评价指标体系如下：

2.2.1 宽严度指标

我们知道在具体到评卷过程中，每个评委对评分标准把握的宽严程度不同，常出现有的偏严格、有的偏宽松情况。有一种倾向是朝着平均数打分，或者尽量多给中间档次的分数，或者确定档次之后，倾向于给该档的中间分，这种中庸的价值取向在统计学中就是用集中趋势去评价，这些评委属|作为衡量严宽度的指标，其中Pki表示第k个于求同思维特点。因此，在这里采用评分均值偏差评委评阅的第i篇论文的均值， 表示第i题网评的平均分。以每份论文的总平均分为参照点，网评评委给分越接近总平均分表示阅卷质量越好，根据此标准将均值偏差标准化为0～1之间的得分。

2.2.2 离散度指标

网评评委阅卷时，与前一种趋中偏好不同的是发散偏好，即相对于给中间分而言，更容易给出两端分值。当然，这种偏好在一定程度上属于求异思维风格。

为了反映这类评委发散的偏好，可以通过将每个网评评委的评分的方差与该篇总方差对比，即来度量，其中表示第k个评委评阅的第i篇论文的方差，表示第i篇论文网评的总方差。当方差偏差较大时，认为该教师的评分具有发散偏好；反之，当方差偏差较小时，认为其评分具有趋中倾向，根据此标准将方差偏差标准化为0～1之间的得分。

2.2.3 可靠度指标

对于每一个评委来说，评阅的每份论文的评分与其他评阅同一论文的各位评委评分趋于一致时，可以认为该评委的评分是可信的，若与其他评委评分相差较大时，该评委的可信度将会遭到质疑。因此选用克伦巴赫α系数（Cronbacha信度系数）来计算一致性信度系数。Cronbacha信度系数是一套常用的衡量心理或教育测验可靠性的方法，依一定公式估量测验的内部一致性。作为信度的指标，它克服部分折半法的缺点，是目前社会研究最常使用的信度指标，它是测量一组同义或平行测“总和”的信度。克伦巴赫α的原型计算公式为：

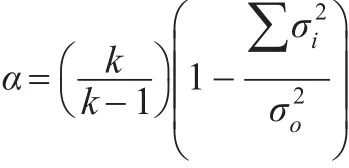
通过克伦巴赫系数α可以检验每个网评评委对每份论文打分与其他网评评委打分情况是否一致，即该网评评委对论文的评判标准与其他网评评委是否一致。若α较低，则表示该网评评委与其他网评评委的一致性较差，若α较高，则表示该网评评委与其他网评评委的一致性较好。

2.2.4 有效度指标

根据数学建模竞赛的评分规则，评分过程中标准差阀值一般不能大于论文满分的1/6。为判断评分是否有效，即判断若干个评委评分的标准差是否超过阈值。用每篇上每个评委的有效阅卷数量与总数量的比值计为有效评分率。数据值越大，有效阅卷越多，表示阅卷质量越好。

计算公式：有效度=每个评委有效阅卷数量/每个评委总工作量。

2.2.5 准确度指标

为了检验网评评委评分对最终成绩的预见性，考虑到获奖情况为有序离散变量，这里以网评评委评分为自变量，以最终成绩为因变量，引入有序Logit模型来描述评分准确性。有序Logit模型是二项分布的logit回归向多项分布的推广，有序Logit模型基本原理如下：

假定对于第 i个论文，因变量Yi有4个取值：0，1，2，3（分别对应未获奖、三等奖、二等奖、一等奖）自变量为Xi，则有序logit回归的模型为：

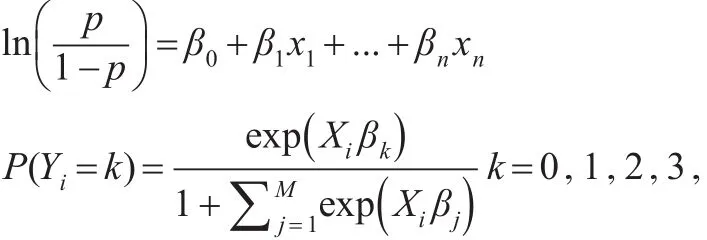
其模型产生的伪R2系数表明了自变量对因变量的解释能力，因此本文选取伪R2系数来描述网评评委评分的准确性。

在回归分析中，判决系数R2和修正后的判决系数伪R2是度量回归方程拟合程度的一个重要统计量。将按网评评委分组的打分和最终成绩构建有序logit回归模型，并得出检验值伪R2。伪R2同样可度量logit回归模型的拟合程度，伪R2值高，则模型拟合得好，在网评评委评分过程中则可说明评分的准确性较高；反之则模型拟合较差，在网评评委评分过程中则可说明评分的准确性较低。

2.3 综合评价结果

根据前述的遗传算法和投影寻踪模型，利用MATLAB软件对某省组织的研究生数学建模竞赛中196名网评评委综合素质进行评价。

通过图1可以看出，遗传算法在迭代了20次后就已经收敛，此时的适应度函数即目标函数值为0.0088，通过目标函数值的比较（0.0088＞0.0081）也可以看出，遗传算法迭代收敛过程的优劣可见一斑。

因此，采用遗传算法得到的投影寻踪综合评价模型的结果：

其中：A1、A2、A3、A4、A5分别为标准化后宽严度、离散度、可靠度、有效度、准确度的各指标值。从模型参数重要性看 A2＜A5＜A4＜A3＜A1。说明宽严度和可靠度是影响投影特征值的两个重要参系数。

将各投影指标带入公式，可以得到各样本的投影特征值画出的排序散点图,如图2所示。

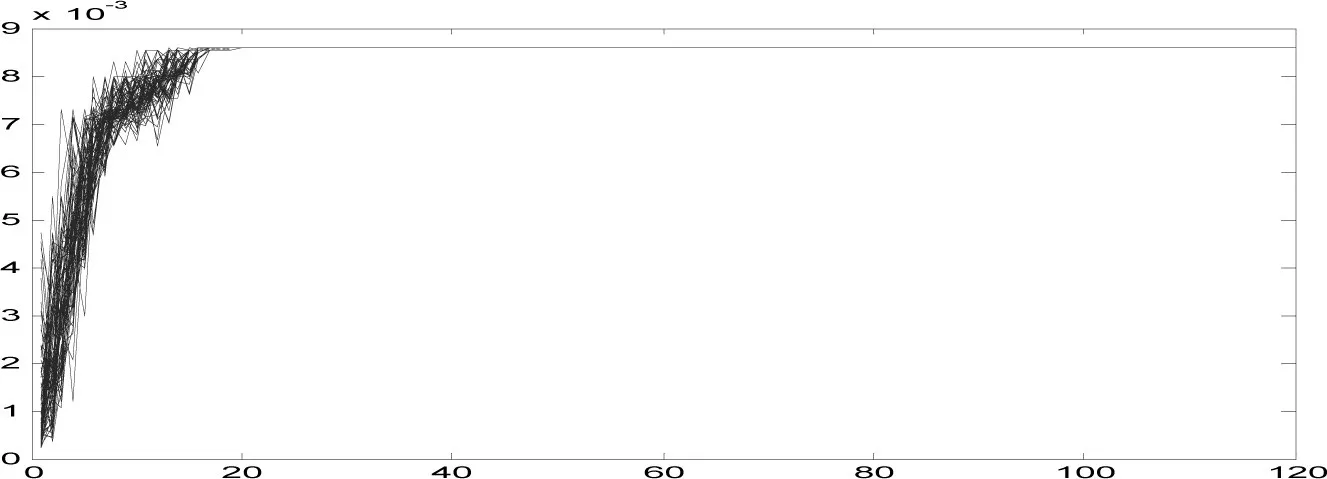
图1 遗传算法迭代收敛过程

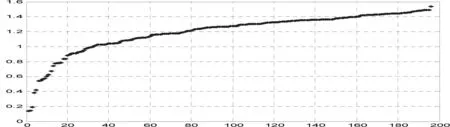
图2 基于遗传算法的投影特征值

根据图2投影特征值的分布判断，遗传算法的效果较为理想。为了更加直观，本文将前十名和后十名网评评委的各指标与投影特征值分别列于后文表1和表2及图3中。前十名投影特征值在1.47～1.54之间，后十名投影特征值在0.14～0.60之间。前、后十名之间相差近1个单位，说明群组内聚集的密度较大，但群组间的区分明显，由此基于遗传算法的投影寻踪模型能有效地对不同网评评委基本素质进行评价。

图3 前十名、后十名投影特征值图

2.4 综合评价分析

通过表1和表2的结果发现投影特征值越大的网评评委综合素质越高，反之，投影特征值越小的网评评委综合素质越低。将前、后十名的网评评委投影特征值与评委基本素质指标的对比分析如下：

（1）前十名网评评委综合素质分析（见下页表1和图4）。在前十名评委中五个指标只有离散度和准确度有些差异，其他三个指标均差异很小。说明他们的共同特点是兼顾求同思维与求异思维，综合素质较高。如专家E22宽严度为0.99963，离散度得分为0.68712，表明他的评分与E组专家打分的总体表现极为接近，其有效度为1表明没有出现过无效评分，准确性为0.867，表明其网评打分能够很好地预见最终的成绩。

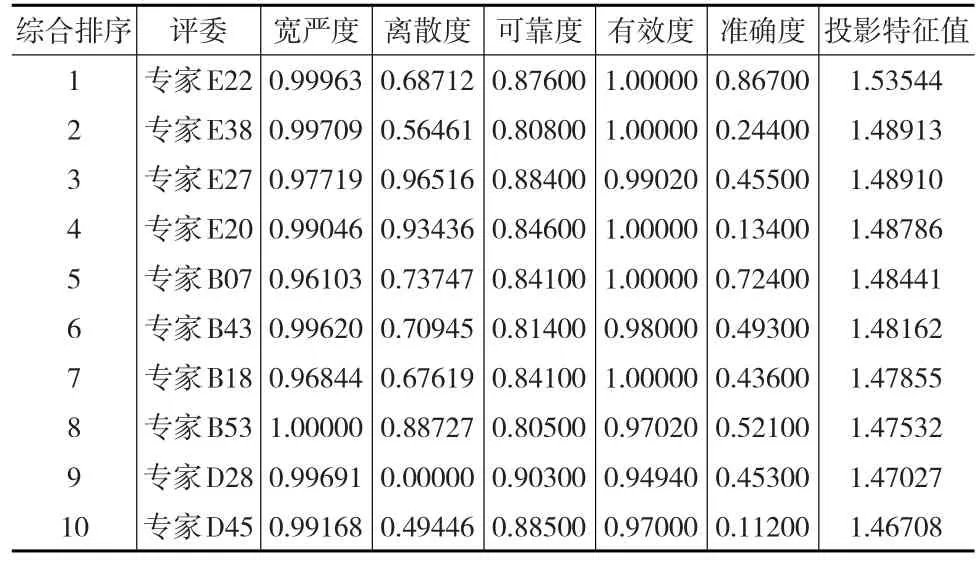
表1 前十名网评评委投影指标

图4 前十名网评评委投影指标图

（2）后十名网评评委综合素质分析（见表2和图5）。在后十名评委中五个指标的宽严度、离散度和准确度均表现出明显的差异。说明这些评委有点偏求同思维、有点偏求异思维、有的两者均不考虑，尤其是第三种评委可能对某一竞赛领域缺乏经验或不熟悉，因此在综合素质体现就较低。如表现最差的是专家E28，其宽严度得分仅为0.0000，离散度为0.17021，表明他的打分与E组专家打分的总体表现相差较大；有效度为0.66010，表明其有接近三分之一的评分属于无效评分。

表2 后十名网评评委投影指标

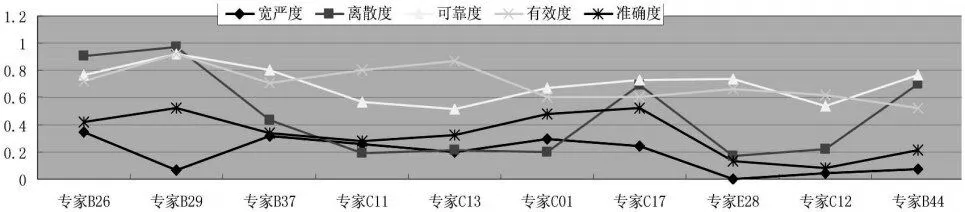
图5 后十名网评评委投影指标图

3 结论与建议

本文首次将投影寻踪法引入到对网评评委综合素质评价中来，也是一次大胆的尝试。本文遵循了样本数量为指标个数的3～5倍以上计算结果具有稳键性的基本要求，建模使用了196个专家的评分数据。模型结果显示：评委的综合素质特别优秀和较差的均为少数，即1.0及以下和1.4及以上的均为30人左右，分别占15.3%，近70%网评评委综合素质相差不大，基本呈现正态分布趋势，这与实际相符的，表明该模型评价取得了较理想的结果。因此，投影寻踪法模型是一种科学、合理的综合评价方法。

本文结合评价结果，提出以下几点建议：（1）建立各类网络评委专家库。因竞赛种类繁多，为了使各类竞赛有序进行，建立各类竞赛相关的网评专家库，对每次网评评委的表现差异进行评价、遴选，不断完善和更新网评专家库。（2）建立网络专家评分管理系统、完善网络评委评分标准。该系统能够根据评分标准对异常评分进行筛选和剔除，并按规则自行调整。（3）构建合理的评价指标体系也是综合评价的关键所在。根据没有差异就没有统计的原则，在对现有提取的五个指标进行充分研究的基础上，对各个样本差异小的指标建议删去，补充其他相关指标，以确保综合评价的全面性。（4）完善评价等级划分。在最终结果的评价上只进行了综合素质高低的排序未划分明确的等级，它对于遴选网评评委有很重要的参考价值。

[1]陈正伟.新编统计学[M].北京:北京邮电大学出版社,2012.

[2]吴喜之.复杂数据统计方法——基于R的应用[M].北京:中国人民大学出版社,2013.

[3]付强,赵小勇.投影寻踪模型原理及其应用[M].北京:科学出版社,2007.

[4]毛紫阳,吴孟达.基于序关系的竞赛网评评委评价方法[J].数学的实践与认识,2006,（10）.

[5]卓金武.MATLAB在数学建模中的应用[M].北京:北京航空航天大学出版社,2010.

[6]赵海燕,芮南.双评作文题网上阅卷评卷教师评卷水平评价维度的确定[J].评价与测量,2009,（2）.

[7]程毛林,韩云.基于投影寻踪主成分分析法的综合国力评价模型研究[J].淮阴师范学院学报:自然科学版,2015,（1）.

[8]易昆南.残缺数据的论文名次及评委水平的评判与逆判[J].湘潭大学自然科学学报,2005,（2）.

[9]龚千健,王涛,裴莹莹.打分机制公平性评估的概率统计模型[J].数学建模及其应用,2013,（2）.

[10]徐翠霞,樊小东.关于高校讲课竞赛评审机制的思考[J].黑龙江教育,2012,（8）.