基于前景理论的灰区间语言变量随机多属性决策模型

赵 敏，弓箭峰，王利东

（大连海事大学a.数学系；b.信息科学技术学院，辽宁 大连 116026）

0 引言

传统的多属性决策通常利用的集结方法是期望效用理论，而期望效用理论的前提是人的行为是完全理性的[1]。1979年Kahneman和Tversky提出的前景理论（Prospect Theory）[2]改善了期望效用理论的缺陷，因此具有更强的普适性。目前，前景理论得到广泛关注，已被应用于动态路径选择行为问题[3]、模拟人的认知行为[4]、应急决策[5]、银行贷款意向评估[6]等，并结合其他理论扩大其应用范围[7-9]。苏宇和刘培德充分研究了梯形模糊数和梯形模糊语言变量下的随机模糊多属性决策问题，提出基于前景理论的随机模糊多属性决策方法[1,10]；Liu和Jin针对属性值为不确定语言变量的随机风险决策问题并结合前景理论扩展了已有的多属性决策方法[7]。

由于前景理论能够表示人在决策问题中的不完全理性行为，本文在以上的工作基础上，构建区间概率条件下基于前景理论的决策模型。考虑到在实际决策过程中，对于一个特定的决策问题，其决策基础是已获得的信息，而这些信息往往是不完整的，会对决策的可信度造成影响，本文采用的灰区间就可以很好地表达这种信息完整度即决策可信度。

1 理论基础

1.1 区间概率

定义1[8]：一个可以描述基本事件的概率实数区间集[Li，Ui]（i=1，2，...，n）被称为n 维区间概率 （n-PRI），如果满足：对任意的 （i=1，2，...，n）均有 0≤Li≤Ui≤1。

定义2[7]：一个 n-PRI（L，U）是有理的，如果满足：存在一组正实数使得（i=1，2，...，n）；否则，n-PRI（L，U）是无理的。

将区间概率转换成点概率能大大减少计算量。文献[9]给出了一种C-OWA集成算子方法。

1.2 C-OWA集成算子

1.3 区间灰色语言变量

定义 3[10]：若一个灰色模糊数的模部是一语言变量灰部为闭区间那么为灰区间语言变量。

区间灰色语言变量的灰部用来衡量所获得的信息量的多少。灰度大小与信息量的多少成反比[4]。

定义 4[10]：设两个区间灰色语言变量则区间灰色语言变量的海明距离为：

1.4 前景理论

基于前景理论选择备选决策方案主要依据加权前景函数值进行排序[2]。前景函数值V可由下述公式得到：

其中概率权重函数w（p）是对于 p的单调递增函数，决策者主观感受的前景价值函数v（Δx）是x与参考点x0的差分的函数，Δxi=xi-x0。

x是相对于参考点的收益（正）与损失（负）。α和β分别代表了风险态度系数 （0≤α≤1，0≤β≤1）值越大，则表明决策者越倾向于冒险。θ为风险规避系数，θ＞1时表明决策者对风险更加敏感。很显然，v（0）=0。在本文中，采用Kahneman和Tversky给出的系数α=β=0.88，θ=2.25[2]。

（2）概率权重函数[11]

（1）前景价值函数

其中，w+（p）和（p）分别是收益和损失的非线性权重函数，γ是风险收益态度系数，δ是风险损失态度系数。Kahneman和Tversky[11]认为 γ=0.6，δ=0.72，Richard和Wu[12]认为γ=0.74，δ=0.74。本文将采用γ=0.74，δ=0.74。

2 决策模型

2.1 决策问题描述

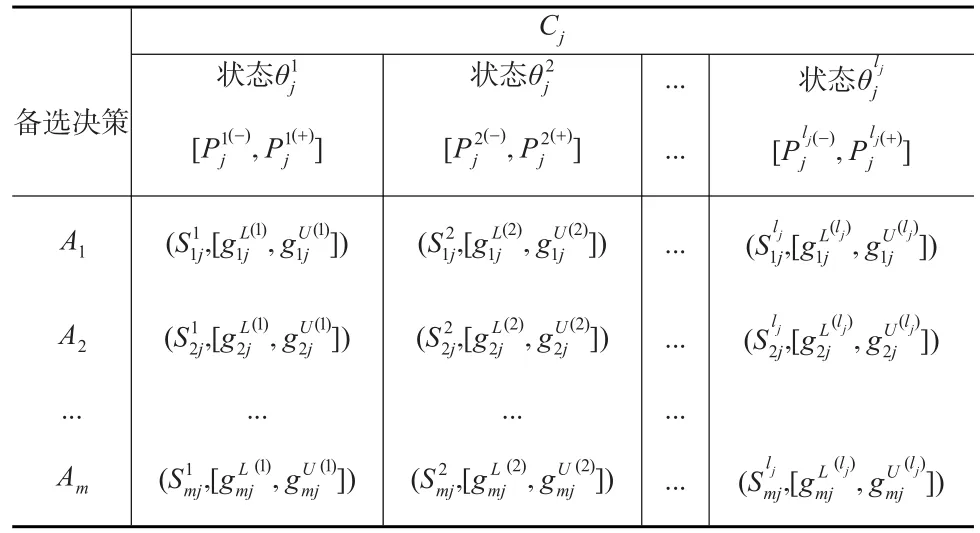
表1 备选决策在属性Cj的lj个状态下的决策信息 j=1，2，...，n

2.2 决策步骤

（1）指标规范化

对于评价指标可以分为效益型指标和成本型指标，语言值代表的实际意义也有可能是不一样的，这就需要对属性值进行标准化处理去除量纲。本文中属值均为效益型，采用的语言变量均为（“非常差”，“很差”，“比较差”，“一般”，“比较好”，“很好”，“非常好”），因此不需要进行标准化。

参考点的选取有很多方法，例如，取零点、取均值、取中间值、最差点、最优点。本文将针对每个属性选取最优点为其参考点。因在语言变量中，语言值越大代表该备选决策在特定属性下越占优势，且灰度越小表明信息越完整，数据可信性越高，因此其理想最优参考方案确定方法如下:

（3）计算距离

（4）计算前景价值函数

（5）将区间概率转化为点概率（6）计算概率权重函数

（7）计算前景函数值

（8）计算加权前景函数值

获得属性权重 ω=（ω1，ω2，...，ωn），则加权后的前景函数值为：

（9）将Zi的值作为备选决策Ai的排序指标，对应Zi值越小的备选决策越好。

3 实例分析

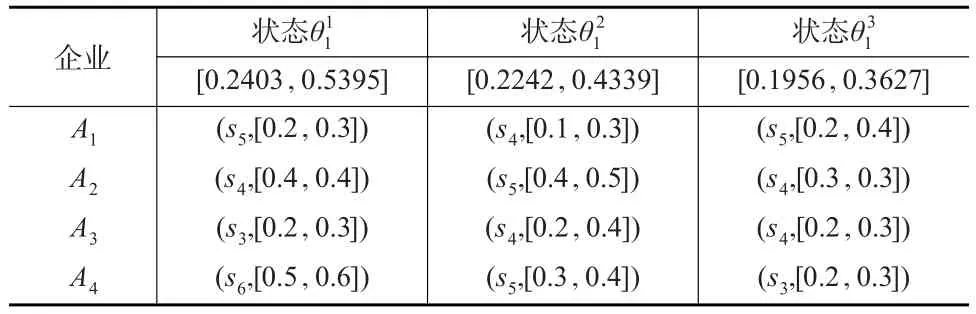
表2 各企业在属性C1的三个状态下的决策信息

表3 各企业在属性C2的三个状态下的决策信息

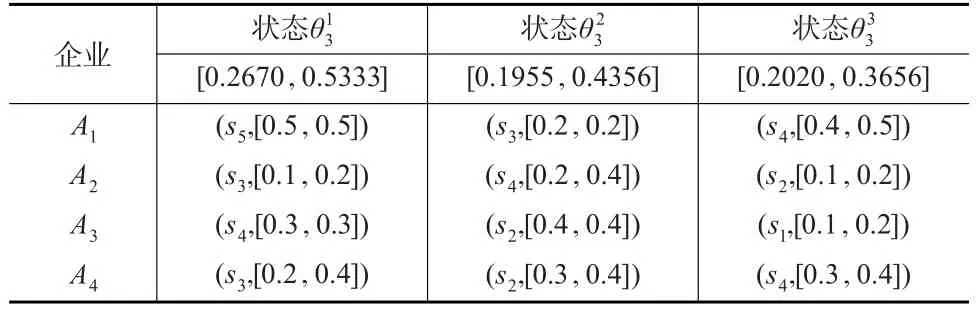
表4 各企业在属性C3的三个状态下的决策信息

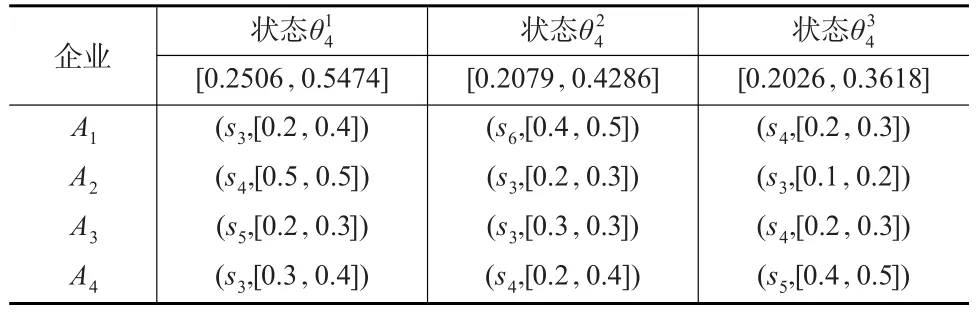
表5 各企业在属性C4的三个状态下的决策信息

（1）由 公 式 （7）至 公 式 （9）计 算 得 到 参 考 向 量 为 ：[（s6，[0.1，0.3]），（s5，[0.1，0.2]），（s5，[0.1，0.2]），（s6，[0.1，0.2]）]；

（2）计算每个属性值到对应参考点的距离：

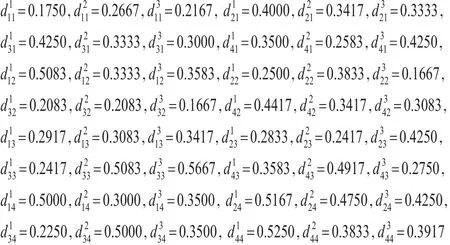
（3）计算前景函数值

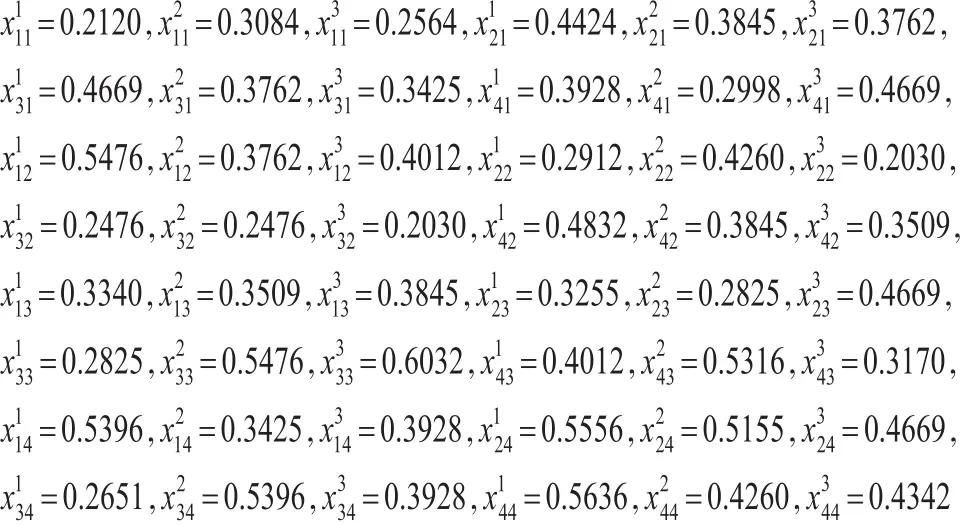
（4）将区间概率转化为点概率

转化得到的点概率为：

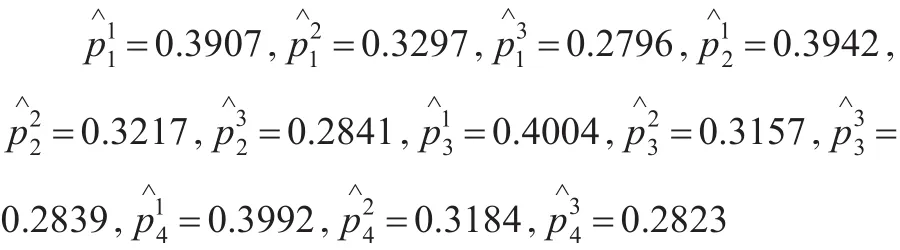
（5）计算概率权重函数

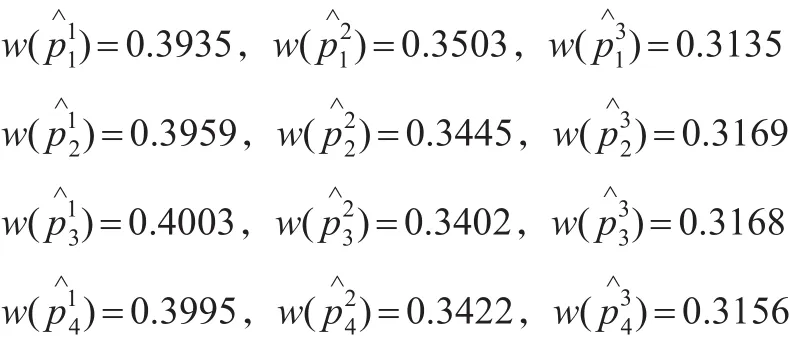
（6）计算前景函数值

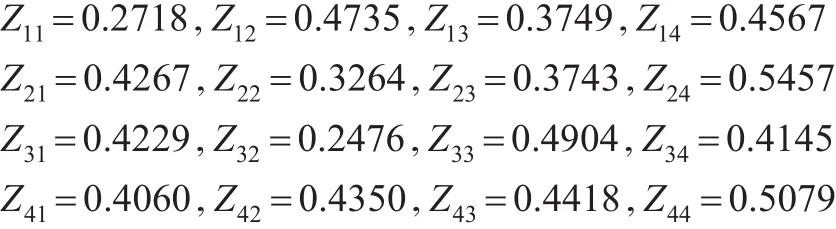
（7）属性权重可由主客观相结合的方法得出，为与参考文献结果对比，本文选用文献[13]中的属性权重为ω=（ω1，ω2，ω3，ω4）=（0.1850，0.3200，0.3290，0.1660），则计算得到的综合前景值为：

Z1=0.4010， Z2=0.3971， Z3=0.3876， Z4=0.4440

（8）将综合前景值作为指标进行排序，最终结果为：

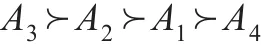
（9）结果分析

由于本文选取的实例数据依据的实际背景来源于文献[13]，并加入区间概率考虑评价的数据的随机性，且所得到的结果与文献[13]得到排序结果一致，一定程度上展示了所建立的考虑随机环境下的决策模型的有效性。本文结合了前景理论研究多属性决策，更好地表达了人的行为的不完全理性，并根据实际情况调整属性权重、区间概率，使得模型具有可调节性。

4 结论

本文将灰区间语言变量多属性决策模型扩展到随机概率环境下的灰区间语言变量随机多属性决策模型。所构建的模型中引入了区间概率，体现属性值状态概率不确定性的情况，并结合前景理论构建了更加普适的备选方案排序方法。该模型适用于评价信息带有不确定和不完全的多属性决策问题。

[1]苏宇.基于前景理论的随机模糊多属性决策方法的研究[D].济南：山东经济学院，2011.

[2]Kahneman D,Tversky A.Prospect Theory:An Analysis of Decision Under Risk[J].Econometrica,1979,47 （2）.

[3]张波.基于前景理论的动态路径选择行为研究[M].上海:上海交通大学,2012.

[4]Mengov G.Prospect Theory—A Milestone.Intelligent Systems Refer⁃ence Library,2015,89.

[5]Wang L,Zhang Z X，Wang Y M.A Prospect Theory-Based Interval Dynamic Reference Point Method for Emergency Decision Making[J].Expert Systems With Applications,2015,42（23）.

[6]Lin X D,Cheng L,Mao W T,Qiu Z W.Research On Measuring The Bank's Loan Willingness Based on Prospect Theory.2015,12th Inter⁃national Conference on Service Systems and Service Management（IC⁃SSM）,22-24 June 2015,pp.1-5

[7]Liu P D,Fang J.Research on the Multi-attribute Decision-making Under Risk With Interval Probability Based on Prospect Theory and the Uncertain Linguistic Variables[J].Knowledge-Based Systems,2011,（24）.

[8]He D Y.Decision-making Under the Condition of Probability Interval By Maximum Entropy Principle[J].Operations Research and Manage⁃ment Science,2007,（16）.

[9]王丹丹.基于灰数旳随机决策方法及应用研究[D].长沙:中南大学商学院,2013.

[10]刘培德,张新.一种基于区间灰色语言变量几何加权集成算子的多属性群决策方法[J].控制与决策,2011,26（5）.

[11]Tversky A,Kahneman D.Advances in Prospect Theory:Cumulative Representation of Uncertainty[J].Journal of Risk and Uncertainty,1992,（5）.

[12]Richard G,Wu G.On the Shape of the Probability Weighting Func⁃tion[J].Cognitive Psychology,1999,（38）.

[13]王会东,刘培德,李成栋等.一种基于区间灰色梯形模糊数的多属性群决策方法[J].内蒙古大学学报:自然科学版,2014,45（1）.