等价无穷小量代换及泰勒公式在极限运算中的应用

2018-01-05李珊栗巧玲余旭洪

数学学习与研究 2018年21期

关键词：极限

李珊栗巧玲余旭洪

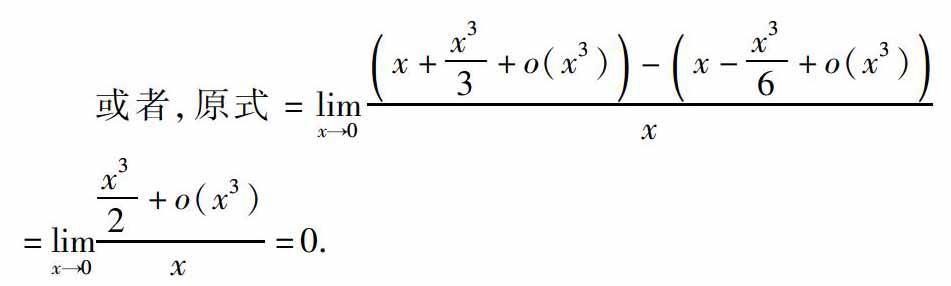
【摘要】本文提出了等价无穷小量代换的一个重要结论以及等价无穷小与泰勒公式的关系.

【关键词】等价无穷小量;泰勒公式;极限

【基金项目】国家自然科学基金（11601331，11601332），上海高校青年教师培训资助计划.

高等数学的研究对象是变量，研究方法是无穷小分析法，也就是极限方法，掌握好极限概念与极限运算是从初等数学迈入高等数学的一个重要阶梯.求解极限的方法有很多，但选择适当的方法直接关系到运算过程的简便程度和运算结果的正确性.利用等价代换求解极限是指将一些无穷小量用与其等价的无穷小量来替代，从而简化运算[1-3]，但是遇到分式中的加减项的时候不能随便套用等价无穷小.

例1 求 lim x→0 tanx-sinx sin3x .

错误解法当x→0时，tanx～x，sinx～x，

∴原式=lim x→0 x-x x3 =0.

正确解法当x→0时，tanx～x，sinx～x，1-cosx～ 1 2 x2，

∴原式=lim x→0 tanx（1-cosx） x3 =lim x→0 1 2 x3 x3 = 1 2 .

分析错误在于认为当x→0时，tanx～x，sinx～x，则有tanx-sinx～x-x=0，即错误地认为无穷小量的代换可以任意地应用到极限运算中，并忽视了在等价无穷小代换中，分子、分母必须是相同无穷小量的同阶形式，也就是说如果按照错误的解法进行无穷小替换之后，分子是关于x的一阶无穷小，而分母是关于x的三阶无穷小，则分子与分母的比值应该为∞，这与无穷小等价替换的定理二[1]相矛盾，定理二指出：设α～α ～，β～β ～，且lim β ～ α ～存在，则lim β α =lim β ～ α ～ .即利用等价无穷小做代换，就必须满足替换后的极限必须是存在的.

这个题目应用泰勒公式的计算方法为：

原式=lim x→0 x+ x3 3 +o（x3） - x- x3 6 +o（x3） x3

=lim x→0 x3 2 +o（x3） x3 = 1 2 .

也就是说和差不能代换的原因是tanx-sinx= x3 2 +o（x3）.

根据上例，我们得到一个有用的定理.

定理 α，β，α ～，β ～为同一变化过程中的无穷小量，且α，β为同阶无穷小，又α～α ～，β～β ～ .

（1）当lim β α ≠-1时，则 α+β γ ～ α ～ +β ～ γ ;

（2）当lim β α ≠1时，则 α-β γ ～ α ～ -β ～ γ .

证明由已知lim β α =a，lim β′ β =1，则当a≠-1时，

有lim α ～ +β ～ γ α+β γ =lim 1+ β ～ α 1+ β α = lim 1+ β ～ β · β α lim 1+ β α = 1+a 1+a =1，

即当lim β α ≠-1时，则 α+β γ ～ α ～ +β ～ γ .同理可证（2）.

由该定理我们可以看出上述例子的错误在于，首先，lim -sinx tanx =-1不满足该定理的条件，所以不能随意利用等价无穷小量代换;其次，该定理的应用和分母γ没有必然的联系.