ABAQUS混凝土塑性损伤因子计算方法及应用研究

杨 飞， 董新勇， 周沈华， 黄余冲

(1.西安市地下铁道有限责任公司，陕西西安 710018； 2.长安大学建筑工程学院，陕西西安 710061)

ABAQUS混凝土塑性损伤因子计算方法及应用研究

杨 飞1， 董新勇2， 周沈华1， 黄余冲2

(1.西安市地下铁道有限责任公司，陕西西安 710018； 2.长安大学建筑工程学院，陕西西安 710061)

ABAQUS中塑性损伤模型可有效模拟混凝土在反复荷载作用下非弹性力学行为，在结构抗震性能分析中应用广泛，但该模型中塑性损伤因子确定方法尚存在问题。文章基于GB 50010-2010《混凝土结构设计规范》中的单轴本构关系，提出并推导了计算混凝土塑性损伤模型损伤因子的实用方法，通过钢筋混凝土简支梁数值算例及室内试验对三种混凝土塑性损伤因子计算方法的精度进行了对比研究。结果显示，采用混凝土轴心强度标准值确定塑性损伤因子时，基于过镇海单轴受力模型的能量等效法和GB 50010-2010《混凝土结构设计规范》中单轴本构关系的实用法计算简单，且具有较好的精度，研究结论可为混凝土结构非线性抗震分析提供参考。

混凝土塑性损伤模型； 损伤因子； 计算方法； 数值分析； ABAQUS

近年来，我国西部黄土地区地铁工程逐渐增多，黄土地区地铁地下结构的抗震性能及安全性评价日益受到密切关注[1]。随着地铁地下结构抗震理论与实践不断进步及计算技术飞速发展，数值仿真分析可更全面、更真实再现地铁地下车站、区间隧道等地下结构在地震荷载下的动态特性，被国内外科研工作者普遍采用。ABAQUS大型非线性有限元分析软件，在处理黄土介质变形及土-结构动力相互作用的非线性问题时具有较好的适用性，因此在黄土地区地铁地下结构抗震研究中应用广泛。

ABAQUS提供了丰富的材料库，其中混凝土塑性损伤模型为混凝土结构抗震性能研究提供了可靠途径。该模型基于塑性损伤因子考虑材料刚度折减，能够较准确、方便地模拟混凝土及其它脆性材料在反复荷载下的损伤退化。该软件的用户手册对混凝土塑性损伤模型的基本理论及相关参数进行了详细的介绍，但对模型中塑性损伤因子的取值未做明确规定，然而数值分析结果的准确性与塑性损伤因子的取值密切相关[2]。相关研究中混凝土塑性损伤模型的塑性损伤因子计算方法各不相同，且在确定塑性损伤因子时采用的混凝土强度代表值也不统一，张劲[3]采用图解法原理和孟宪春[4]采用能量等效法计算混凝土塑性损伤因子时分别选取轴心强度标准值和平均值作为混凝土强度代表值。本文以西安黄土地区地铁车站抗震研究为背景，提出并推导一种基于GB 50010-2010《混凝土结构设计规范》[5]附录C中混凝土单轴本构关系确定塑性损伤因子的实用方法，并通过混凝土简支梁算例及室内试验对三种混凝土塑性损伤因子计算方法的模拟精度进行对比研究。结果显示，采用混凝土轴心强度标准值确定塑性损伤因子时，基于过镇海单轴受力模型的能量等效法和GB 50010-2010《混凝土结构设计规范》的实用法计算简单，具有较好精度，研究结论可为混凝土结构非线性抗震分析提供参考。

1 ABAQUS中混凝土塑性损伤模型

ABAQUS中混凝土塑性损伤模型(以下简称CDP模型)是建立在Lubliner[6]和Lee and Fenves[7]模型基础上的。该模型基于各向同性假设，采用弹性损伤结合受拉及受压塑性替代混凝土的非弹性行为，并考虑了由于拉伸或压缩过程中塑性应变导致的弹性刚度退化及循环荷载作用下的刚度部分恢复。

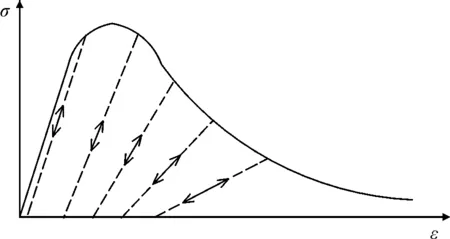
单轴往复荷载作用下，CDP模型中混凝土塑性损伤演化及刚度恢复如图1所示。轴向受拉过程中，混凝土未到达峰值拉应力(A点)前，拉应力线性增加，峰值拉应力过后，混凝土开始出现裂缝，材料产生受拉损伤并不断累积。受拉加载至B点卸载时，将按有效刚度(1-dt)E0产生回弹，即图1中路径BC。当荷载由拉力状态转变为压力状态时，拉伸裂缝在压力作用下闭合，引起受压刚度恢复(wc=1)，此时加载路径为CMF。受压加载至F点卸载时，混凝土发生了受压塑性损伤，有效刚度退化至(1-dc)E0。当荷载由压力状态再次转变为拉力状态时，裂缝并未闭合，拉伸刚度未得到恢复，应力应变路径沿为GH(wc=0)[8]。

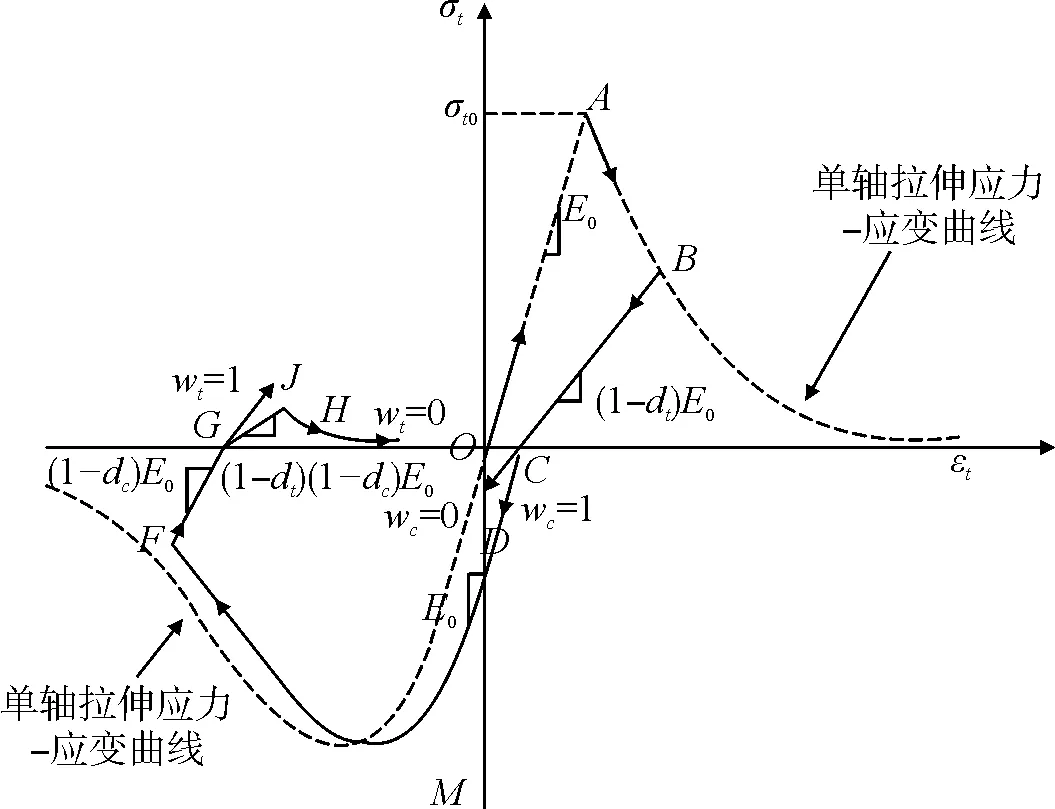
图1 混凝土弹性模量恢复示意

ABAQUS中CDP模型是基于单轴受力状态定义，受压塑性变形阶段材料损伤演化可用非弹性应变与受压损伤因子关系曲线定义，受拉开裂阶段材料损伤发展可用开裂应变与受拉损伤因子关系曲线定义。

2 塑性损伤因子的计算方法

2.1 基于过镇海单轴受力曲线的能量等效法

能量等效原理由Sidoroff于1981年提出，即应力作用在无损材料与作用在受损材料所产生的弹性余能在形式上相同[9-10]，只要将Cauchy应力改为等效应力，并考虑刚度折减将初始弹性模量取为等效受损弹性模量。根据能量等效假设，材料的应力应变关系可表示为：

σ=E0(1-d)2ε

(1)

基于过镇海单轴受力曲线[11]和能量等效假设，可得混凝土受压塑性损伤因子见式(2)、式(3)：

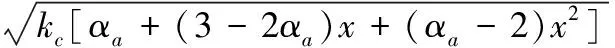
(2)

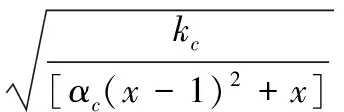
(3)

混凝土受拉损伤因子见式(4)：

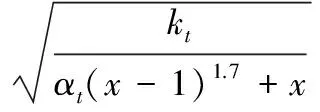
(4)

2.2 基于过镇海单轴受力曲线的图解法

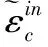
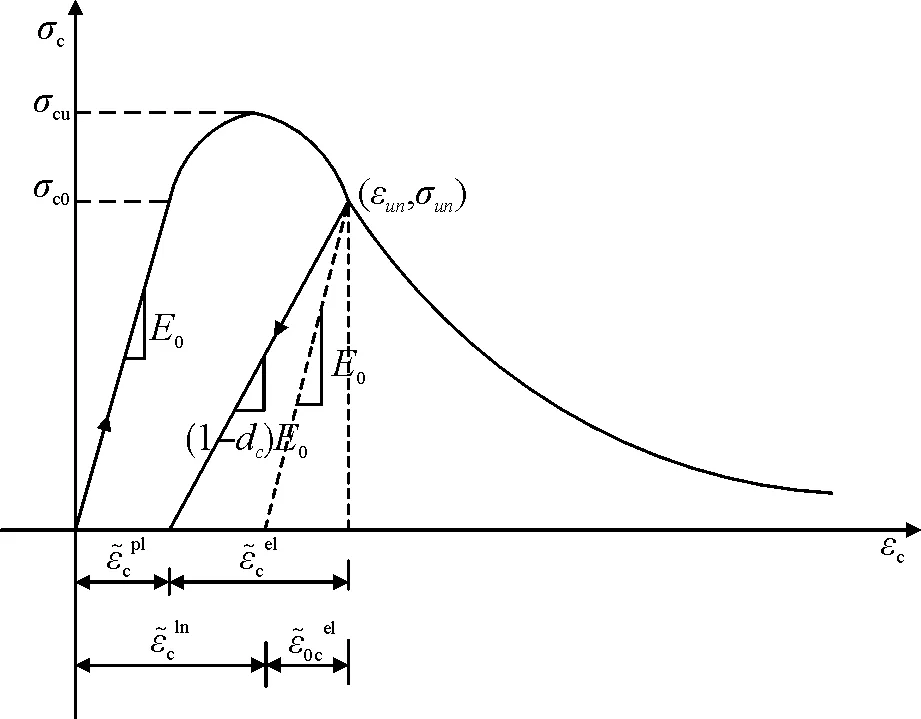
图2 混凝土单轴受压损伤演化

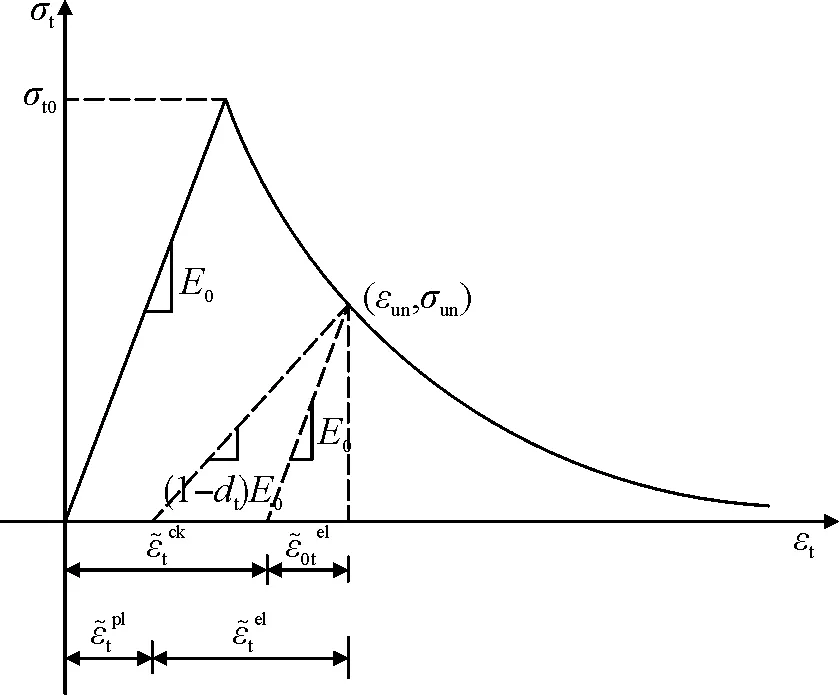
图3 混凝土单轴受拉损伤演化

由图中的几何关系可得受压和受拉塑性损伤因子见式(5)：

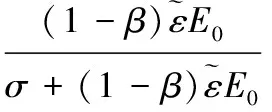
(5)

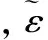
2.3 基于GB 50010-2010规范的实用法

我国现行GB 50010-2010《混凝土结构设计规范》(以下简称“10混规”)中混凝土单轴应力应变曲线如图4所示[5]。单轴受压曲线方程如式(6)：

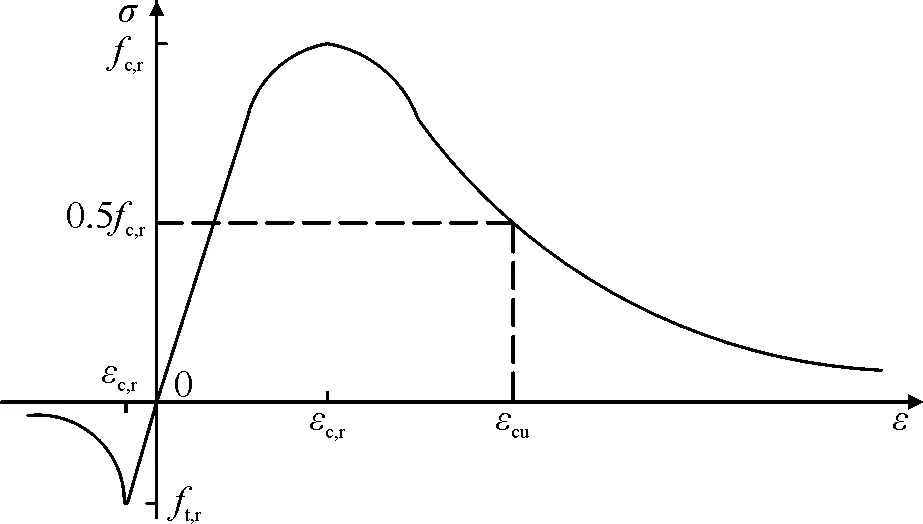
图4 GB 50010-2010中混凝土单轴本构曲线

(6)

单轴受拉曲线方程如式(7)：

σt=Ec(1-Dt)εt

(7)

其中D取值可按“10混规”中的方法计算，式中用参数D表示混凝土损伤演化参数，以区别于ABAQUS中CDP模型的塑性损伤因子d。为将“10混规”中的损伤演化参数用于ABAQUS中CDP模型，需建立“10混规”中损伤演化参数与CDP模型塑性损伤因子之间的关系。

Lemaitre在1971年从细观尺度分析，并提出描述材料损伤的应变等效原理，可反映出材料的损伤演化过程[14]。该原理假设材料在有效应力下产生损伤后，其应变与无损伤应变等效。根据应变等效原理，可由无损伤材料的本构关系导出损伤材料的本构关系，其中应力要用等效应力代替。根据应变等效假设可得式(8)：

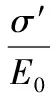
(8)

从而，材料的应力应变关系可表示为式(9)：

σ=E0(1-D)ε

(9)

从式(9)中分析发现，基于应变等效假设的材料损伤演化过程中无塑性应变，是一种弹性损伤模型(图5)。由式(6)、式(7)与式(9)的对比分析可知，“10混规”提出的单轴受力本构模型中的损伤演化参数D是基于应变等效假设的弹性损伤参数，不同于CDP模型中的塑性损伤因子d(图5)。

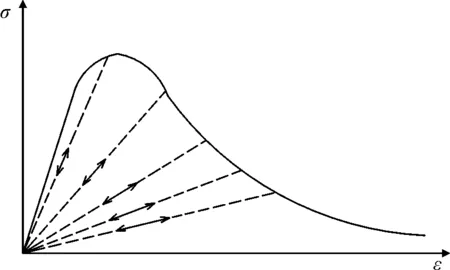
(a) 弹性

(b) 塑性图5 弹、塑性损伤模型示意

对比分析能量等效假设与应变等效假设，发现有如下关系见式(10)：

E0(1-D)=E0(1-d)2

(10)

从而推出式(11)：

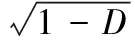
(11)

因此，“10混规”提出的单轴受力本构模型中的损伤演化参数D不能直接用于CDP模型，将其按式(11)转换为塑性损伤因子之后，可用于ABABQUS中CDP模型。

3 三种混凝土塑性损伤因子算法的对比分析

上述三种塑性损伤因子的计算均需确定混凝土单轴强度代表值，可结合“10混规”取轴心强度标准值或平均值。为了对比分析不同计算方法及不同单轴强度代表值确定混凝土塑性损伤因子的可靠度，本文采用不同方法确定混凝土塑性损伤因子，基于ABAQUS的CDP模型，对钢筋混凝土简支梁受力变形过程进行了数值分析，并通过室内承载力试验验证数值分析结果，研究不同塑性损伤因子确定方法的精度。

3.1 CDP模型中塑性损伤因子的计算

以C30混凝土为例，采用“10混规”中的轴心强度标准值和平均值分别计算CDP模型塑性损伤因子。C30混凝土轴心抗压强度标准值为20.1 MPa，轴心抗拉强度标准值取为2.01 MPa；轴心抗压强度平均值为28.0 MPa，轴心抗拉强度平均值取为2.80 MPa；混凝土泊松比取0.2。

为方便表述，本文将能量等效法、图解法及基于“10混规”实用法的计算结果分别用A、B和C表示，用角标1和角标2分别表示采用混凝土轴心强度标准值和轴心强度平均值的计算值。混凝土塑性损伤因子计算结果如图6、图7所示。

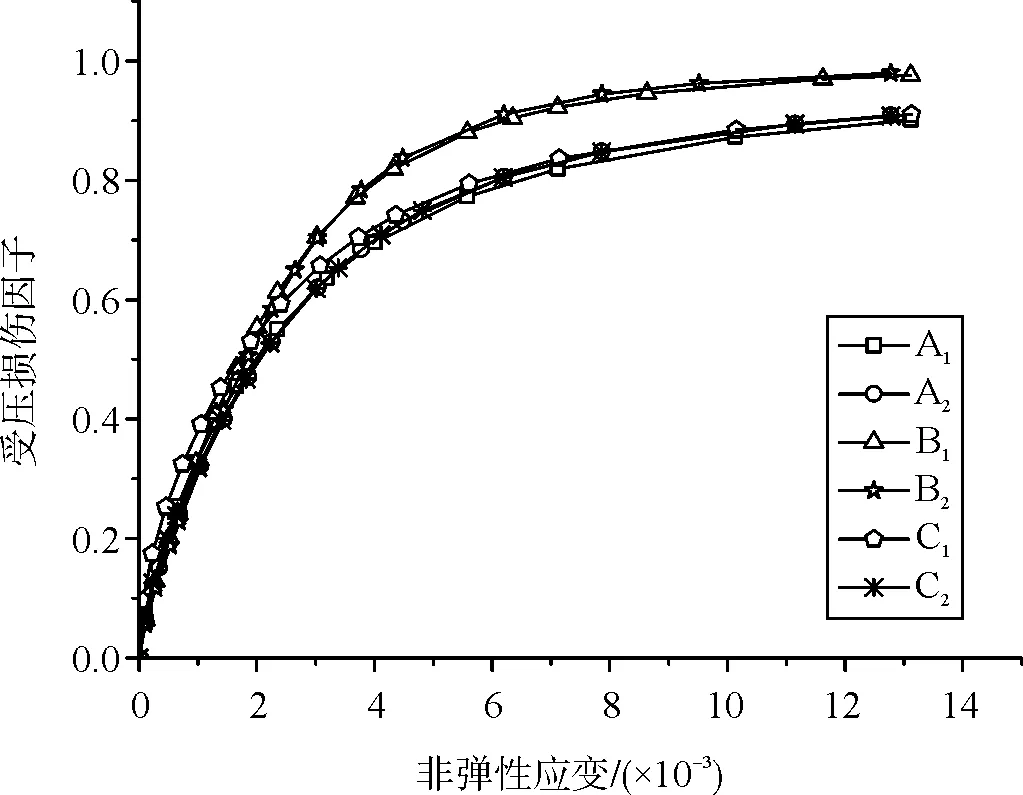
图6 非弹性应变-受压损伤因子关系曲线

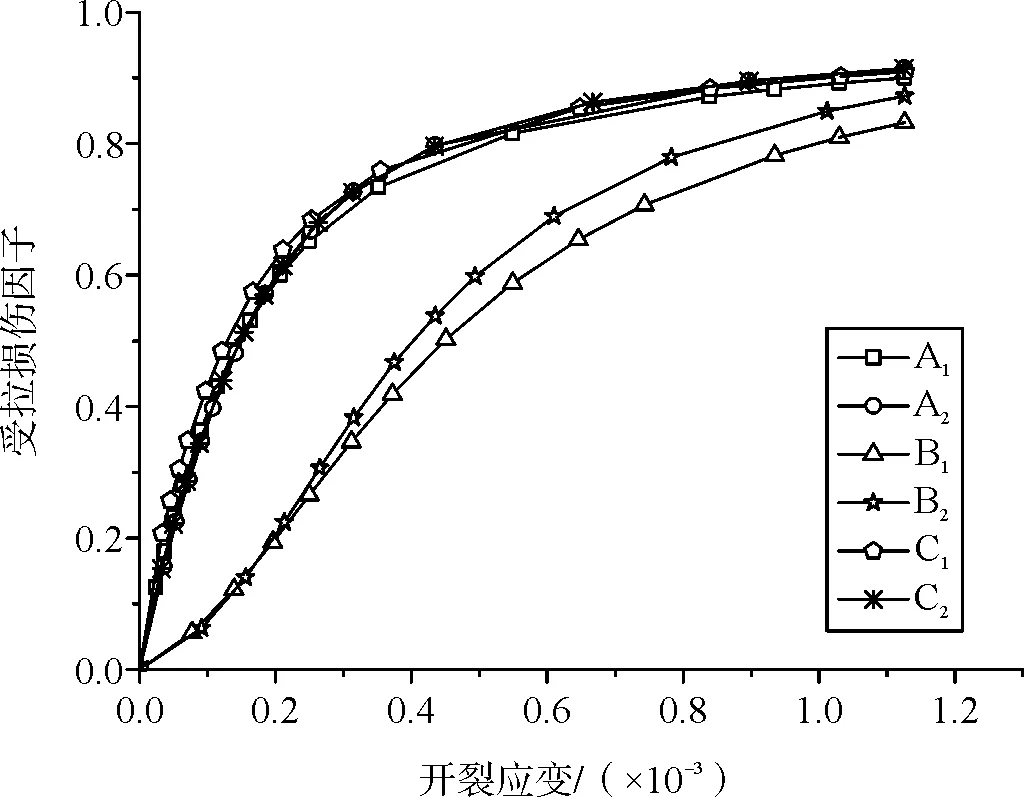
图7 开裂应变-受拉损伤因子关系曲线

3.2 数值分析及试验模型

在ABAQUS中建立钢筋混凝土简支梁模型，截面及配筋如图8所示。为了防止混凝土简支梁局部受压破坏，在支座和加载点设置厚度为6 mm的钢垫板。简支梁所用混凝土为C30，采用ABAQUS中的CDP本构模型，使用三维8节点缩减积分实体单元C3D8R模拟；纵向钢筋及箍筋强度标准值为300 MPa，采用Plasticity本构模型，使用三维2节点桁架单元T3D2模拟；采用Interaction模块中Embedded将钢筋骨架嵌入混凝土中，模拟两者之间的约束变形机理；钢筋混凝土简支梁室内试验模型尺寸及配筋同数值分析模型。

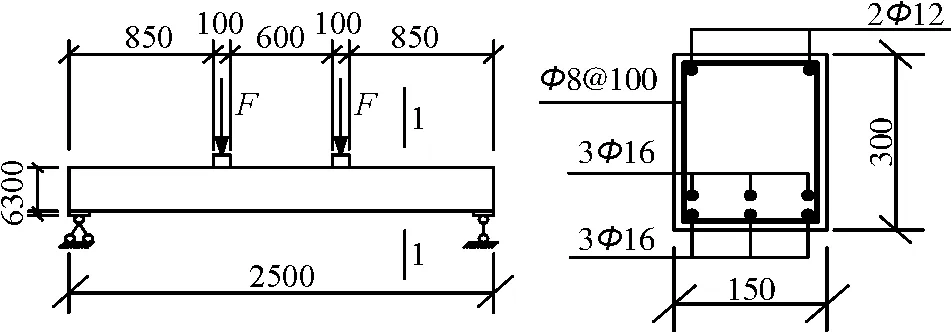
图8 钢筋混凝土梁及配筋示意

3.3 结果分析

采用不同方法确定CDP模型的塑性损伤因子，分别计算钢筋混凝土简支梁荷载-挠度曲线(图9～图10)。当采用混凝土轴心强度标准值确定CDP模型塑性损伤因子时，钢筋混凝土梁的荷载-挠度曲线呈现出明显的屈服平台，发生了较大的塑性变形，即梁破坏形态属于适筋梁延性破坏。当采用混凝土轴心强度平均值确定CDP模型塑性损伤因子时，钢筋混凝土梁的荷载-挠度曲线呈现出明显陡直跌落特征，即梁发生脆性破坏。

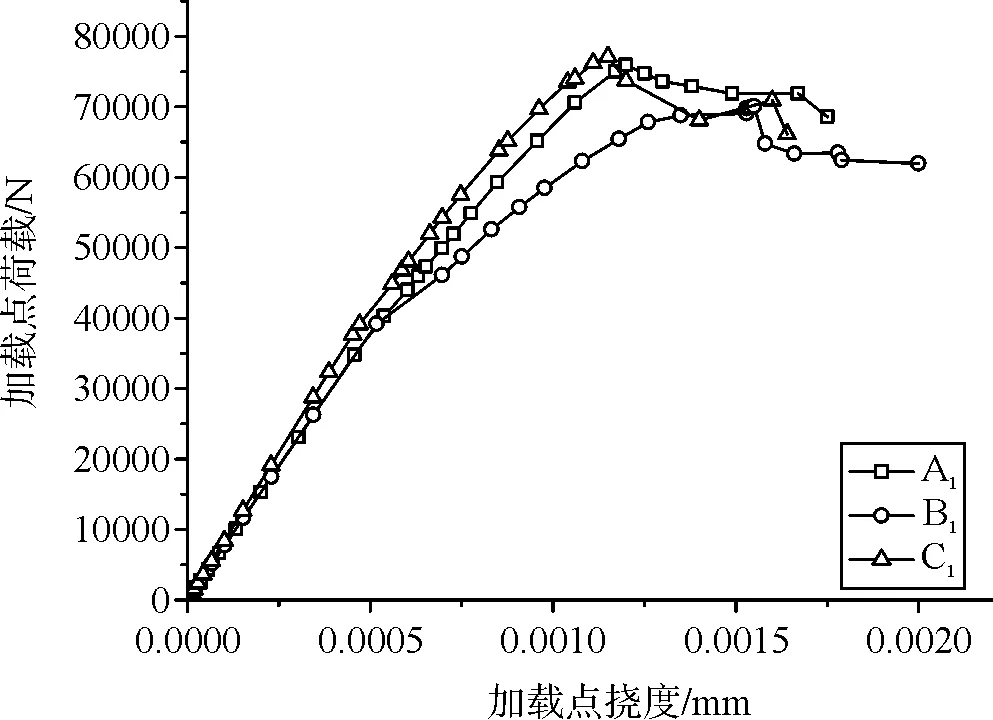
图9 基于轴心强度标准值的分析结果

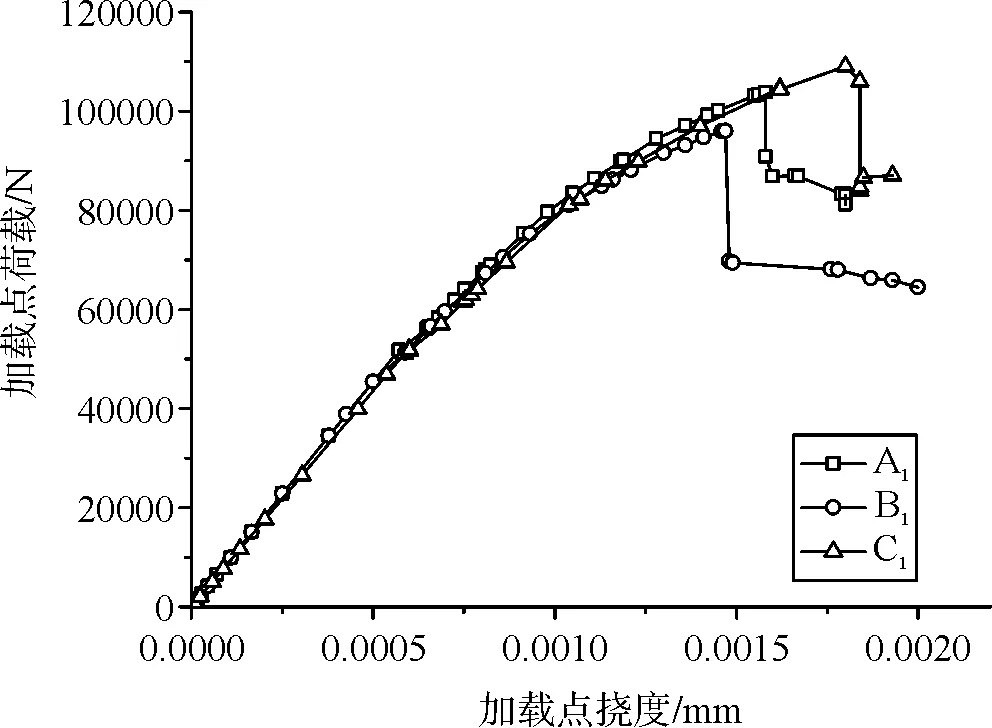
图10 基于轴心强度平均值的分析结果

为了验证数值分析结果，按数值模型中的尺寸、材料及配筋浇筑钢筋混凝土简支梁试件，并进行了室内承载力试验，其破坏形态为延性破坏。基于轴心强度标准值确定CDP模型的塑性损伤因子，数值分析结果可反应钢筋混凝土梁的实际受力水平，其破坏形态与试验结果相符；而基于轴心强度平均值确定塑性损伤因子，数值分析中混凝土的强度高于实际值，从而使分析结果呈现出少筋梁的脆性破坏形态。因此，可推断在ABAQUS中应用CDP模型时，基于混凝土轴心强度标准值确定塑性损伤因子，具有较好的可靠性。

由钢筋混凝土简支梁的破坏荷载，可计算出该梁所承受的极限弯矩。将数值分析得出的计算极限弯矩与室内试验获得的极限弯矩进行对比分析，可得不同方法确定塑性损伤因子时，数值分析结果相对于室内试验结果的误差，对比分析结果见表1。基于轴心强度标准值确定混凝土塑性损伤因子时，数值分析计算极限弯矩与室内试验中极限弯矩较接近，相对误差为0.97 %～6.7 %；而基于轴心强度平均值确定混凝土塑性损伤因子时，数值分析结果与试验值有较大差距，极限弯矩相对误差为20.6 %～37 %，进一步验证了基于混凝土轴心强度标准值确定塑性损伤因子，具有较好的可靠性。从钢筋混凝土梁极限弯矩分析结果可知，基于轴心强度标准值确定混凝土塑性损伤因子，采用基于过镇海单轴受力曲线的等效能量法和基于“10混规”的实用法时，数值分析计算极限弯矩与室内试验中极限弯矩的相对误差分别为0.97 %和2.6 %，均具有较高的精度。

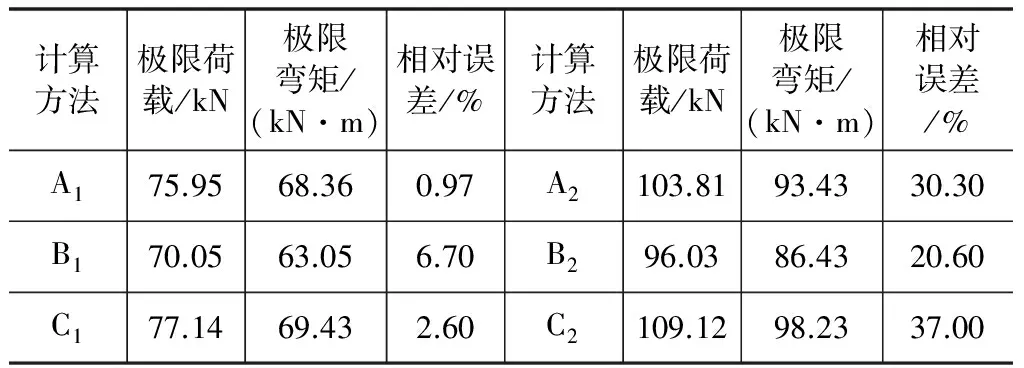
表1 不同混凝土塑性损伤因子计算方法的分析结果

4 结论

本文提出了基于“10混规”计算ABAQUS中CDP模型塑性损伤因子的实用方法，并通过钢筋混凝土简支梁数值算例和室内试验对能量等效法、图解法和基于“10混规”的实用法计算CDP模型塑性损伤因子的可靠性进行了对比研究，可为混凝土结构非线性抗震分析提供参考，得出以下结论：

(1)对比分析表明，基于轴心强度标准值确定CDP模型塑性损伤因子时，数值模拟的破坏形态与室内试验相同，且数值计算的极限弯矩与试验值相对误差较小，为0.97 %～6.7 %；基于轴心强度平均值确定CDP模型塑性损伤因子时，数值计算极限弯矩与试验值相差较大，为20.6 %～37 %，且数值模拟破坏形态与实际破坏形态不同。因此，基于混凝土轴心强度标准值确定CDP模型塑性损伤因子，具有较好的可靠性。

(2)确定混凝土塑性损伤因子时，发现“10混规”中单轴受力模型提供的损伤演化参数D描述的损伤过程中不发生塑性变形，属于弹性损伤模型，由此推导了将其转化为塑性损伤因子的计算公式，提出了基于“10混规”计算ABAQUS中CDP模型塑性损伤因子的实用方法。同时，数值模拟与室内试验结果的对比分析表明，基于“10混规”的实用法确定CDP模型塑性损伤因子具有较高的模拟精度。

(3)基于“10混规”的实用法与能量等效法、图解法相比，在ABAQUS数值建模与计算中具有计算方便、收敛较快的优点。

(4)本文对比了三种塑性损伤因子计算方法的数值模拟结果，对ABAQUS中CDP模型塑性损伤因子的取值提出有益的建议，有利于在混凝土材料非线性抗震分析中得到可靠的结果。

[1] 权登州, 王毅红, 井彦林, 等.黄土地区地铁车站数值模型及测试位置研究[J].震灾防御技术, 2015, 10(1): 108-115.

[2] 秦浩,赵宪忠.ABAQUS混凝土损伤因子取值方法研究[J].结构工程师,2013,29(6):27-32.

[3] 张劲,王庆扬,胡守营, 等.ABAQUS混凝土损伤塑性模型参数验证[J].建筑结构,2008,38(8):127-130.

[4] 孟宪春,景立平.多层地铁车站振动台试验与数值分析[D].哈尔滨：中国地震局工程力学研究所，2011: 31-46.

[5] GB 50010-2010 混凝土结构设计规范[S].

[6] LUBLINER J, OLIVER J, OLLER S, et al. A plastic-damage model for concrete [J]. International Journal of Solids and Structures, 1989, 25(3): 299-326.

[7] LEE J, FENVES G. Plastic-damage model for cyclic loading of concrete structures [J]. Journal of Engineering Mechaniccs, 1988, 124(8): 892-900.

[8] ABAQUS Inc. Abaqus analysis user.’s manual [M]. 2010.

[9] KRAJCINOVIC D, FONSEKA G. The continuous damage theory of brittle materials, Part 1: General Theory [J]. Journaal of Applied Mechanics, 1981, 48(4): 809-815.

[10] 曹明.ABAQUS损伤塑性模型损伤因子计算方法研究[J].道路工程，2012(2) : 51-54.

[11] GB 50010-2002 混凝土结构设计规范[S].

[12] 陆新征,叶列平,缪志伟, 等.建筑抗震弹塑性分析[M].北京：中国建筑工业出版社，2009: 121-125.

[13] 张劲,王庆扬,胡守营, 等. ABAQUS混凝土损伤塑性模型参数验证[J].建筑结构,2008,38(8)：127-130.

[14] 李兆霞.损伤力学及其应用[M].北京：科学出版社，2002: 16-19.

[定稿日期]2017-07-28

国家自然科学基金资助项目(编号：41472267)；西安市地下铁道有限责任公司科研基金项目(编号：D4-YJ-042014048)

杨飞(1983～)，男，本科，工程师，主要从事地下结构抗震设计方面工作;董新勇(1990～)，男，硕士研究生，主要从事建筑结构抗震、混凝土结构以及生土结构方面研究；周沈华(1980～), 男，硕士，高级工程师，主要从事岩土与地下工程抗震研究。

TU311.4

A