动静载作用下预应力注浆锚索治理巷道中底锚索的动态响应
2018-01-05裴晨浩
金 亮,裴晨浩
(河南理工大学 土木工程学院,河南 焦作 454000)
动静载作用下预应力注浆锚索治理巷道中底锚索的动态响应
金 亮,裴晨浩
(河南理工大学 土木工程学院,河南 焦作 454000)
为了研究在动静载作用下预应力注浆锚索治理巷道中底锚索的动态响应,本文以常村煤矿S61#为研究对象,采用FLAC数值软件进行模拟分析得:在动载作用下,预应力注浆锚索的前3段轴向应力比较大,受到动力扰动的影响比较深,最大减小幅度能达到18.4%,底臌治理前应考虑底锚索前3段的轴向应力;由于在巷道底板采用了注浆的治理方法,所以底锚索的第1段水泥浆应力为零,且不受动力扰动的影响;在动载作用下,底锚索的第2段与第3段水泥浆应力呈拉压应力交替出现形式,后4段对应的水泥浆应力始终为拉应力。
巷道工程;动静载;预应力注浆锚索;动态响应;数值模拟
锚杆与锚索在边坡、煤矿巷道和隧道等方面得到了非常普遍的使用。关于锚杆与锚索的力学性能国内外学者进行了非常丰富的研究。在静载方面,康红普[1]通过理论计算与数值模拟分析了锚杆在不同应力状态下的应力分布特征。在动载方面,单仁亮[2]通过具体的试验得到在爆炸荷载作用下锚杆的轴向应变和弯曲应变特征,以及锚杆的振动频率分布规律;王光勇[3-4]通过数值软件LS-DYNA研究出在顶爆和拱腰侧爆作用下,拱顶、拱腰、拱脚和侧墙锚杆的轴向应力分布规律。王正义[5]主要研究在冲击地压作用下围岩的变形破坏特征和锚杆的动态响应,得出侧向位置锚杆轴向应力呈“双峰”的特性。这些都是关于在动载作用下锚杆的动态响应研究,而关于锚索[6]的动态响应研究却特别少。
本文以常村煤矿S61#回风上山巷为研究对象,采用预应力注浆锚索技术进行治理,并且专门针对其底锚索的动态响应进行研究,为实际的巷道生产设计提供指导。
1 数值模型
1.1 标准模型及参数选择
以常村煤矿S61#回风上山巷为标准模型,巷道沿着距离煤底板2.5 m掘进,具体物理力学指标如表1所示。通过对围岩中应力分布影响范围分析,取模型尺寸长1.8 m,高40 m,宽60 m。巷道的设计断面为矩形,其高和宽分别为3.5 m、5 m。巷道的原有支护形式是锚杆锚索联合支护,锚索在顶帮加强支护,锚索的直径为16.8 mm,长度为6.3 m,锚索的间距为2 000 mm,排距为900 mm;锚杆分布在顶板和左右两帮,锚杆的直径为22 mm,长度为2.4 m,其间距为900 mm,排距为900 mm,如图1所示。底臌治理采用预应力锚索加注浆方法,注浆厚度400 mm,锚索预应力200 kN,具体的尺寸及位置如图2和表2所示。

图1 原巷道支护图 图2 治理后巷道支护图

表1 工程地质参数

表2 锚杆与锚索材料参数
1.2 本构模型及边界条件
静载时,在模型的上边界施加9.261 MPa来模拟垂直方向的力,水平方向施加10.775 MPa水平应力,其他3个边界的约束条件为位移约束。在动静作用时,由于当动力源比较远时,可以将远处的动力扰动近似的等效为平面波,故在模型底部施加平面波。为了更好模拟出半无限体中的应力波传播规律,把数值模型左右边界、上边界设置为粘滞吸收边界。
2 数值结果分析
2.1 关于底锚索的轴向应力分析
为研究预应力注浆锚索的治理效果,现将3根底锚索a、b和c全部平均分为7段,从锚头至锚端依次记为1、2、3、4、5、6和7,将3根锚索每段的轴向应力时程曲线取出,如图4所示。并且分别将3根锚索每段的最小拉应力取出进行分析,如表3、表4和表5所示。从表3、表4、表5可以看出:3根锚索的初始值都是静态下的轴向应力,这3根锚索的前三段应力皆比较大,应力值大致保持在1 200 MPa左右,而剩下4段的应力值则随着距离巷道底板越远就越小,从900 MPa左右开始,历经600 MPa左右、400 MPa左右依次减小到100 MPa左右。由压应力时程曲线我们可以知道压应力是在13 ms左右传到巷道底板,应力时程曲线如图3所示。从图3可以看出,压应力在10 ms时就已经传到底锚索部位,并对底锚索的拉应力产生了影响,具体为这3根锚索都是在前3段减小最多,由于第1根锚索与第3个根锚索关于ZOY这个平面对称,因此其值大致相同,其第1段减小到979.6 MPa,减小幅度能达到18.4%,第2段与第3段减小幅度相同,随着距离巷道底板距离变远,底锚索后面4段的轴向拉应力减小幅度越来越小,逐渐减小到最后一段的12.2%,第2根锚索与其余两根锚索规律相同。从每根锚索的前3段可以看出,差不多每隔10 ms,压应力就出现一次小波动,并且随着时间的推移幅度逐渐减小,推测应是动力余波影响所致。三根底锚索的动态响应大致相同,其对应的前3段在静态时受较大拉应力,在动态作用下拉应力也是波动最大,因此不论是静态还是动态考虑底锚索前3段的锚固力是有意义的,而3根锚索前3段动力扰动余波的影响不容忽视。

表3 第1根锚索的轴向应力最小峰值

表4 第2根锚索的轴向应力最小峰值

图3 3根锚索每段的轴向应力时程曲线

表5 第3根锚索的轴向应力最小峰值
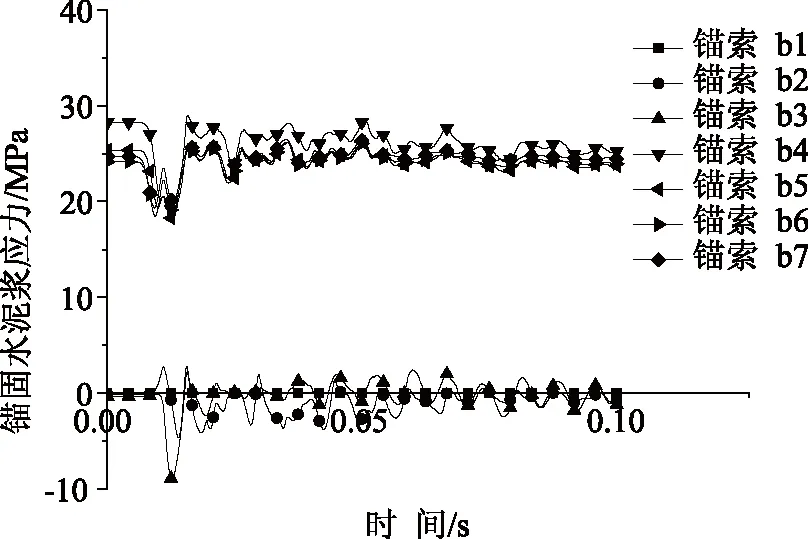
图4 三根锚索每段的水泥浆应力时程曲线
2.2 底锚索的水泥浆应力分析
为了分析水泥浆粘结应力的动态响应,依次将3根底锚索各段的应力时程曲线取出,如图4所示。为了分析3根底锚索的水泥浆粘结应力,将3根底锚索2 ms、10 ms、10.3 ms、10.5 ms、12 ms和50 ms的水泥浆应力图取出,如图5所示。从图4和图5可以看出,在2 ms时对应的3根锚索各段的粘结应力基本上持平,也即没有发生变化,应力波并没有传播到巷道底部,因此在巷道四周正处于静态,粘结应力对应的也没有发生变化;3根底锚索的第一段在静态有一个突出特点就是第一段的水泥浆应力为零,造成这种现象的原因是在Z方向0 m~0.4 m的底板注浆范围内由于岩体的粘聚力增强,从而“替代”了水泥浆应力的作用。这三根锚索的后四段自始至终对应的水泥浆压力均为拉应力。从8 ms开始最前端的应力波传到底锚索下部,其对应的拉应力开始减小,在12 ms时,达到最小值,此时后四段对应的水泥浆应力值皆在20 MPa左右,减小幅度最大能达到33.3%。
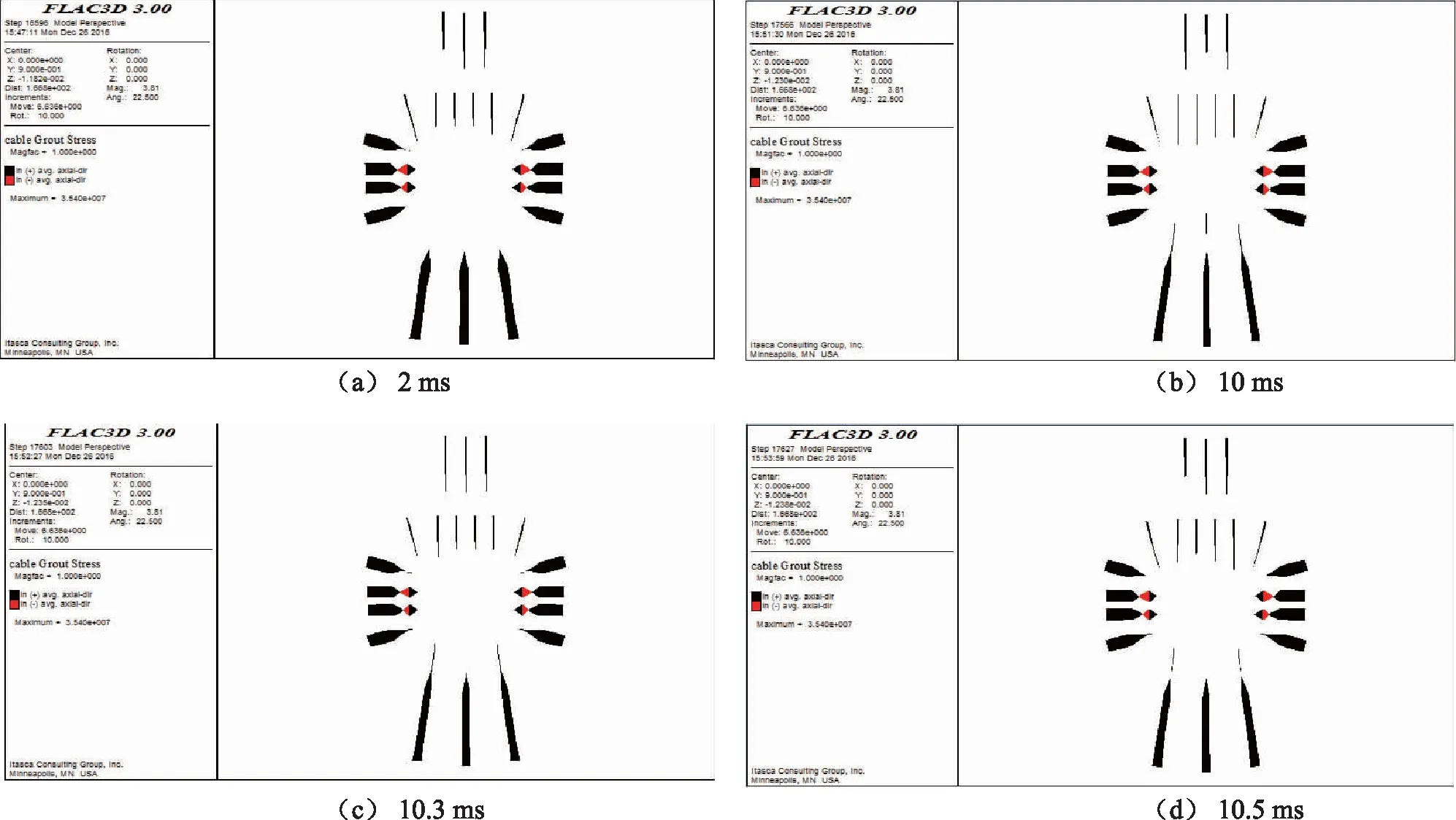
图5 三根锚索的水泥浆应力图
每根底锚索前3段中的第1段由于注浆加固,不受压应力波的影响,一直保持为零;3根底锚索剩下的第2段和第3段因为处于主动区,所以其刚开始受到的应力为压应力,然后与其余四段一样皆是在8 ms左右受到动力扰动的影响,两者的压应力皆是从时间分别为7.8 ms与8.8 ms时变为中性点,然后变成拉应力,这1 ms的时间差距是由于距离加载面距离不同而造成的;在12 ms左右,由于后续应力波的传播,又分别从拉应力变成压应力,第3段是在12 ms作用达到峰值为8.6 MPa,第2段是在14 ms达到峰值,为4.9 MPa,这3根底锚索后4段的水泥浆应力与锚索轴应力呈大致相同的变化规律;而这3根底锚索的前3段由于注浆加固使得第一段水泥浆应力为零,第2段与第3段的水泥浆应力值也不大,呈拉压应力相互交替的变化规律;锚索轴应力因处于结构单元中,所以其并不受注浆加固的影响,从而表现出正常的变化规律。
3 结 语
(1) 预应力注浆锚索中的底锚索前三段所受轴向应力大,在动静载作用下受到的波动较大,轴向拉应力的最大减小幅度为18.4%,应增强底锚索前三段的锚固。
(2) 在动静载作用下除了要考虑底锚索最大的轴向应力波动,也不能忽视动力余波的影响。由于在底板Z方向0.4 m范围内注浆,所以三根底锚索第一段的水泥浆粘结应力为零,且不受动力扰动的影响。
(3) 在动静载作用下三根底锚索的后四段水泥浆应力在应力波到达时都出现了不同程度的减小,最大减小幅度为33.3%,但始终都保持为拉应力。在动载作用下3根底锚索中的第2段与第3段出现拉压应力交替变化。
[1] 康红普,林健,吴拥政.锚杆构件力学性能及匹配性[J].煤炭学报,2015,40(1):11-23.
[2] 单仁亮,周纪军,夏宇.爆炸荷载下锚杆动态响应试验研究[J].岩石力学与工程报,2011,30(8):1540-1546.
[3] 王光勇,张素华,谢文强.锚杆动载响应和轴向应力分布规律数值分析[J].采矿与安全工程学报,2009,26(1):114-117.
[4] 王光勇,郭晓燕,王超.在拱腰爆炸荷载作用下锚杆动态响应数值分析[J].爆破,2015,32(2):33-38.
[5] 王正义,窦林名,王桂峰.锚固巷道围岩结构动态响应规律研究[J].中国矿业大学学报2016,45(6):1132-1140.
[6] 石玉成,秋仁东,孙军杰.地震作用下预应力锚索加固危岩体的动力响应分析[J].岩土力学,2011,32(4):1157-1162.
[7] 范明建,康虹普,林健.埋深1300m大倾角复合岩层巷道围岩综合控制技术研究[J].采矿与安全工程学报,2015,32(5):706-713.
[8] 高富强,高新峰,康红普.动力扰动下深部巷道围岩力学响应FLAC分析[J].地下空间与工程学报,2009,5(4):680-685.
Dynamic Response of Bottom Anchor of Treatment of Roadway with Prestressed Grouting Anchor Cable under Static and Dynamic Load
JIN Liang
(Henan Polytechnic University,Jiaozuo 454000,China)
In order to study dynamic response of bottom anchor of treatment of roadway with prestressed grouting anchor cable under the action of static and dynamic,in the paper FLAC 3D numerical simulation are employed to study S61# as the research object. Results show that the axial stress of the first three sections of prestressed anchor cable is relatively large under the action of dynamic load,and the influence of dynamic disturbance is relatively deep ,and the maximum reduction can reach 18.4%,and axial stress of the three section of the bottom anchor should be considered before floor heave treatment. Because grouting in roadway floor is adopted,the grout stress of first section of anchor cable is zero without the influence of dynamic disturbance. Under the action of dynamic load,the grout stress of second and third bottom cable is tension and compression alternating,and the grout stress of latter four sections of bottom cable is always tensile stress.
roadway engineering;dynamic and static load;borehole pressure relief;dynamic response;numerical simulation
10.3969/i.issn.1674-5403.2017.03.008
TD353
A
1674-5403(2017)03-0028-05
2017-05-10
金亮(1991-),男,河南信阳人,硕士研究生.主要从事岩土方向方面的研究.
河南省高等学校青年骨干教师资助计划项目(2015GGJS-069).
