图像条带噪声的去除方法
2018-01-05陶胜
陶 胜
(集美大学 理学院,福建 厦门 361021)
图像条带噪声的去除方法
陶 胜
(集美大学 理学院,福建 厦门 361021)
针对传感器平台等条件下产生的图像条带噪声,提出了空间域滤波和频率域滤波相结合的去噪方法。条带噪声具有准周期性,噪声对应于其图像的傅里叶频谱中出现的亮点。基于这一原理,首先对带有条带噪声的图像进行傅里叶变换,并检测亮点所在的位置,然后在空间域对噪声图像进行开关中值滤波,并对滤波结果进行傅里叶变换,最后将噪声图像的频谱中噪声对应的区域用相应的开关中值滤波图像频谱区域进行替换,对替换后的结果进行傅里叶逆变换得到去噪声图像。仿真结果表明,采用空间域滤波和频率域滤波相结合的去噪方法比采用空间域滤波和频率域滤波能够取得更好的去噪效果。
条带噪声;开关中值滤波;傅里叶变换
条带噪声是一种在传感器光、电器件反复扫描目标的成像过程中受扫描探测元正反扫描响应差异、传感器扫描机械运动等多种因素扰动下造成的具有一定周期性、方向性且呈条带状分布的特殊噪声[1]。许多学者对产生条带噪声的原因进行了分析,并对条带噪声的去除方法进行了研究和探讨。比较具有代表性的方法有:直方图匹配法、矩匹配法、傅里叶变换法、自相关插值法等[1-7]。
简单的空间域滤波方法(如中值滤波法等)对去除条带噪声有一定的去噪效果,但会消除图像的部分细节,导致图像变得模糊。而傅里叶变换法是在频域去除噪声的频率成分,然后经傅里叶逆变换到空域获得去噪图像,这类方法的缺点是不容易选择正确的频率成分。
本文采用空间域滤波和频率域滤波相结合的去噪方法。首先对含有条带噪声的图像进行频域分析,然后在空间域对噪声图像进行开关中值滤波,并对其进行傅里叶变换,最后将噪声图像的频谱中噪声对应的区域用相应的开关中值滤波图像频谱区域进行替换,对替换后的结果进行傅里叶逆变换得到去噪声图像。仿真实验结果表明该方法不仅能有效地滤除条带噪声,而且可以较好地保护图像细节。
1 条带噪声及频率域滤波
对于传感器平台等条件下产生的图像条带噪声,可以用如下的模型来描述:
ξ(x,y)=A(MOD(x,Δ)==0.or.MOD(x,Δ+1)==0….or.MOD(x,Δ+n)==0)。
其中:MOD函数为求余函数,A为条带的幅值,Δ为条带的位置,n为条带的厚度。
假定原始图像为f(x,y),则叠加条带噪声的图像为f(x,y)+ξ(x,y),Lenna图像叠加条带噪声的结果如图1所示。
傅里叶变换把图像从空域变到频域,图像的背景区域和缓慢变化部分对应于低频,而它的边缘、细节、跳跃部分以及噪声对应于高频[8]。对于带有条带噪声的图像,由于噪声具有准周期性,噪声频谱与图像的频谱几乎是可分离的。因此,可以通过频域滤波的方法来去除条带噪声。对叠加条带噪声的Lenna图像进行二维离散傅里叶变换得到其傅立叶频谱,如图2所示。从图2可以看出,噪声对应于其傅里叶频域能量谱的纵轴上的一些亮点,并且这些亮点关于原点对称。因为周期噪声在对应于周期干扰的频率处以集中的能量脉冲的形式出现,所以可以用一个选择性滤波器来消除周期噪声。相比于其他滤波器,陷波滤波器能够有效地消减或消除条带噪声。

图1 叠加条带噪声的Lenna图 图2 叠加条带噪声的Lenna图的频谱图
1.1 陷波滤波器
陷波滤波器只针对某些特定的频率点周围的频率进行抑制。由于傅里叶变换是对称的,要获得有效结果,陷波滤波器必须以关于原点对称的形式出现,而且会有两个对称的需要抑制的频率点(u0,v0)和(-u0,-v0)。常用的3种陷波滤波器的传递函数如表1所示[9]。

表1 3种陷波滤波器的传递函数
其中:D0是半径,n为阶数。假定图像大小为M×N,频率矩形的中心移动到点(M/2,N/2),
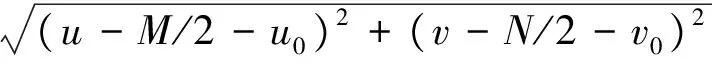
需要说明的是,上述陷波滤波器只列举了一对,而可实现的陷波滤波器的对数可以是多对,而且陷波区域的形状也可以是其他形状,比如区域的形状可以是矩形。另外,陷波滤波器的默认低频位置是在图像的中心,所以在使用陷波滤波器时,图像的频域变换都需要进行中心平移。
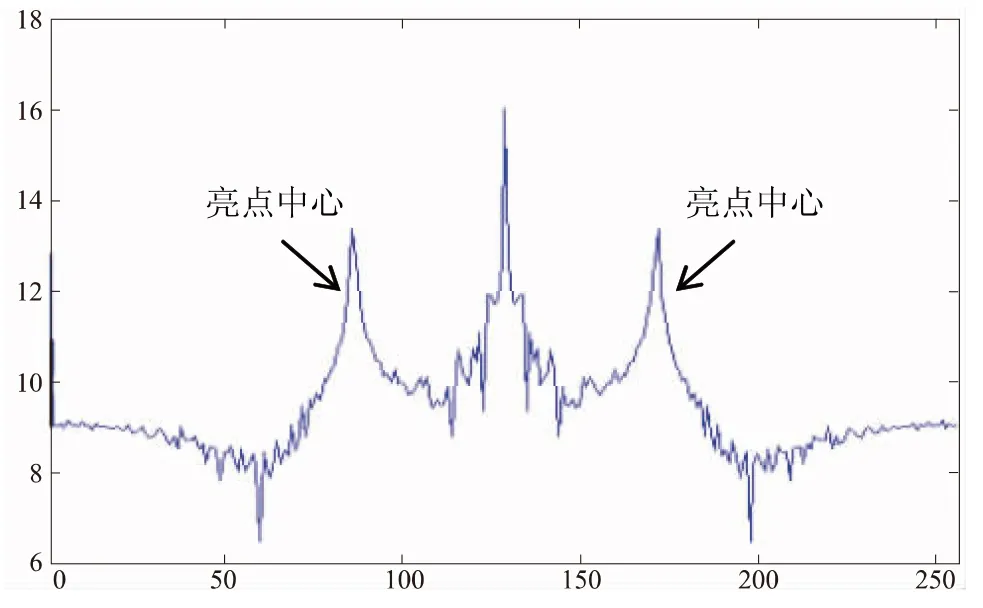
图3 频率分布图
1.2 亮点的检测和陷波滤波器参数的确定
采用陷波滤波器去除条带噪声的关键就在于如何准确地定位噪声对应的亮点,然后确定陷波滤波器参数。
对于叠加条带噪声的图像进行傅里叶变换,其频谱纵轴上的频率分布如图3所示。显然中心位置的点是亮点,但不是噪声所对应的,因此将检测范围限制在纵轴上不包含中心点附近部分的区域,计算其最小值和最大值,分别记为T1和T2,令T=T1+3(T2-T1)/4,如果某点是局部最大值,并且其值大于等于T,那么该点的位置就是亮点中心,如图3所示。对每个亮点中心,计算其与左侧第一个谷底(局部最小值所对应的点)的距离,记为D1,计算其与右侧第一个谷底(局部最小值所对应的点)的距离,记为D2,D1和D2的最大值作为馅波滤波器的带宽半径,这就构造出所需要的陷波滤波器参数(实际应用时可增大一些,效果更好)。
1.3 陷波滤波
检测出噪声对应的亮点位置和确定陷波滤波器参数后,分别采用理想陷波滤波器、巴特沃斯陷波滤波器、高斯陷波滤波器进行滤波。高斯陷波滤波器去除条带噪声的结果如图4所示。
2 空间域滤波
2.1 噪声检测
设噪声图像为f(x,y),大小为M×N。令F(x,y)为噪声标志矩阵,其大小为M×N,初始化值全部为1。对条带噪声图像,首先判断条带噪声的起始位置,从第一行开始,如果下一行的和值与其上一行的和值的差大于等于给定的阈值,则该行就是条带噪声的起始位置。然后确定条带噪声的厚度,从起始位置出发,如果上一行的和值与其下一行的和值的差大于等于给定的阈值,则该行就是该条带的结束位置,起始位置到结束位置的各像素点均为噪声像素,将标志矩阵对应的值修改为0。最后从结束位置的下一行开始,重复这一过程,直到条带噪声图像的最后一行为止。
2.2 开关中值滤波
开关中值滤波器[10]是先进行检测噪声像素,然后只对检测到的噪声像素进行中值滤波,而对于被判断为非噪声的像素不再参与中值滤波。为了能处理边缘点,先要将噪声图像和噪声标志矩阵进行扩展(将噪声图像矩阵和噪声标志矩阵的第一行向上重复3行,最后一行向下重复3行,第一列向左重复3列、最后一列向右重复3列),大小均为(M+6)×(N+6),然后对噪声图像的每一噪声点,考察其3×3的邻域各点,如果这9个点中存在标志为1的点(非噪声点),则去掉这9个点中标志为0的点(噪声点),将剩余点(非噪声点)的像素值的中值作为输出;否则将邻域扩大,考察其5×5的邻域各点,如果这25个点中存在标志为1的点(非噪声点),则去掉这25个点中标志为0的点(噪声点),将剩余点(非噪声点)的像素值的中值作为输出;否则继续将邻域扩大,考察其7×7的邻域各点,如果这49个点中存在标志为1的点(非噪声点),则去掉这49个点中标志为0的点(噪声点),将剩余点(非噪声点)的像素值的中值作为输出。最后,将扩展部分(最上面3行、最下面3行、最左边3列、最右边3列)去掉,剩余部分作为开关中值滤波结果。开关中值滤波去除条带噪声的图像如图5所示。

图4 高斯陷波滤波器去除条带噪声图 图5 开关中值滤波去除条带噪声图
3 空间域滤波和频率域滤波相结合去噪
由图4和图5可知,采用陷波滤波和开关中值滤波的效果并不理想。陷波滤波对去除条带噪声有一定的去噪效果,但会留下一些残余条带,而开关中值滤波消除了图像的部分细节,导致图像变得模糊。为了取得更好的去噪效果,探讨采用空间域滤波和频率域滤波相结合去除条带噪声。
首先对带有条带噪声的图像进行傅里叶变换,然后在空间域对噪声图像进行开关中值滤波,并对滤波结果进行傅里叶变换,如图6所示。再检测图2中亮点所在的位置(即图3中标注的亮点中心),并将图2中纵轴上的亮点区域用图6中对应的区域进行替换,最后对替换后的结果进行傅里叶逆变换得到去噪声图像。采用空域和频域滤波相结合去噪的结果如图7所示。

图6开关中值滤波结果的频谱图 图7空域和频域滤波相结合去条带噪声图
4 仿真实验分析
通常使用峰值信噪比PSNR来评价去噪效果[11]。PSNR越高,则相应的去噪方法性能就越好。
采用MATLAB R2012a作为开发工具,在Windows XP平台下实现了条带噪声的频域陷波滤波去噪、空域开关中值滤波去噪以及空域和频域滤波相结合去噪。仿真实验以Lenna作为原图,分别添加幅值为35、间隔为3、厚度为3的条带噪声(记为条带噪声Ⅰ),添加幅值为30、间隔为3、厚度为4的条带噪声(记为条带噪声Ⅱ),添加幅值为40、间隔为2、厚度为5的条带噪声(记为条带噪声Ⅲ),分别计算出理想馅波滤波、巴特沃斯馅波滤波、高斯馅波滤波和开关中值滤波以及空域和频域滤波相结合去噪的PSNR,如表2所示。

表2 频域和空域去除条带噪声的PSNR
由表2可知,采用开关中值滤波的峰值信噪比采用陷波滤波的峰值信噪比高出2 dB至6 dB左右,而采用空域和频域滤波相结合去噪的峰值信噪比采用开关中值滤波的峰值信噪比高出34 dB至36 dB左右,采用空域和频域滤波相结合去噪能够取得更好的去噪效果。
5 结 语
陷波滤波是去除条带噪声的有效方法,亮点的检测和陷波滤波器参数的确定对于图像的去噪结果起非常重要的作用。采用理想陷波滤波器、巴特沃斯馅波滤波器和高斯馅波滤波器去除条带的差别不大。采用空域和频域滤波相结合去噪能够取得比陷波滤波以及开关中值滤波更好的去噪效果。仿真实验表明,从客观评价标准和主观视觉效果两方面均可以体现空域和频域滤波相结合去噪方法能够较好地去除图像中存在的条带噪声,同时有效地保持图像的细节信息。
[1] 吴军,张万昌.MODIS影像条带噪声去除的自相关插值法[J].遥感技术与应用,2006,21(3):253-258.
[2] Chen J S,Shao Y,Guo H D,et al.Destriping CMODIS data by power filtering[J].IEEE Transactions on Geoscience and Remote Sensing,2003,41(9):2119 -2124.
[3] Gadallah F L,Csillag F.Destriping multisensor imagery with moment matching[C]//Int J Remote Sens,2000,21(12):2505 -2511.
[4] Oimoen M J.An Effective Filter for Removal of Production Artifacts in U.S.Geological Survey 7.5-Minute Digital Elevation Models[C]//In Proc of the Fourteenth International Conference on Applied Geologic Remote Sensing,2000:6-8.
[5] Wegener M.Destriping multiple sensor imagery by improved histogram matching[J].Int J Remote Sensing,1999,11(5):859-875.
[6] 刘正军,王长耀,王成.成像光谱仪图像条带噪声去除的改进矩匹配方法[J].遥感学报,2002,6(4):278 -284.
[7] 孙颖,张志佳.基于频域滤波的自适应条带噪声去除算法[J].仪表技术与传感器,2006(2):57-59.
[8] 李云红,屈海涛.数字图像处理[M].北京:北京大学出版社,2012:107-119.
[9] 杨杰,黄朝兵.数字图像处理及MATLAB实现[M].北京:电子工业出版社,2013:115-119.
[10] 金良海,李德华.基于噪声检测的图像去噪算法[J].模式识别与人工智能,2008,21(3):298-302.
[11] 姚敏.数字图像处理[M].北京:机械工业出版社,2012:118-120.
Denoising Method Based on Stripe Noise Image
TAO Sheng
(Jimei University,Xiamen 361021,China)
The paper proposes the denoising algorithm of combining the spatial domain filtering and frequency domain filtering in order to remove the strip noise under the sensor platform condition. The noise distribution of the image with strip noise is quasi- periodic and the noise corresponds to the bright spots in its Fourier spectrum. Based on this principle,first,the image with strip noise is analyzed,using Fourier transfer,Second,the location of the bright spots is detected and filtered by using switch median filtering in the special domain and then Fourier transform the filtering results. Last,the corresponding regions of noise in the frequency spectrum are replaced with the corresponding frequency spectrum regions of the image with switch median filtering,and the denoised image is obtained by Fourier inverse transforming the filtering results. The simulation results show that the combination of spatial domain filtering and frequency domain filtering can achieve better denoising effects than the spatial domain filtering or frequency domain filtering alone.
stripe noise; switch median filtering; fourier transfer
10.3969/i.issn.1674-5403.2017.03.019
TP391.4
A
1674-5403(2017)03-0074-05
2017-04-25
陶胜(1968-),男,汉族,湖北武穴人,硕士,副教授,主要从事计算机图形图像处理方面的研究.
