耦合复Ginzburg-Landau方程组的拉回吸引子
2018-01-05陈兆蕙吴昌健唐跃龙张星红
陈兆蕙,吴昌健,唐跃龙,张星红
(1. 华南农业大学 珠江学院,广东 广州,510900;2. 湖南科技学院 数学与计算科学系,湖南 永州,425199;3. 北京理工大学 自动化学院,北京,100081)
耦合复Ginzburg-Landau方程组的拉回吸引子
陈兆蕙1,吴昌健1,唐跃龙2,张星红3
(1. 华南农业大学 珠江学院,广东 广州,510900;2. 湖南科技学院 数学与计算科学系,湖南 永州,425199;3. 北京理工大学 自动化学院,北京,100081)
以耦合复金兹堡–朗道(Ginzburg-Landau)方程系统为模型,研究了在周期边界条件下和初始条件下它的拉回吸引子的存在性。主要采用能量方程方法来进行证明:首先证明在W中存在一个闭过程且有界,从而证明该闭过程存在一个拉回吸收集;其次,当满足初值有界条件时,证明该闭过程满足拉回条件C,因此证实了该Ginzburg-Landau方程组存在拉回吸引子。
耦合Ginzburg-Landau方程组;拉回条件C;拉回吸引子
拉回吸引子概念最早由H. Crauel,F. Flandoli等[1–2]提出,近些年,陈兆蕙等[3]研究了耦合非线性Ginzburg-Landau方程组的整体吸引子;王蕊[4]研究了带有可乘白噪音Ginzburg-Landau方程的随机吸引子;而鲍杰等[5]证明了高阶广义2D Ginzburg-Landau 方程的随机吸引子;张元元[6]求证出了一类带Robin边界条件的2维随机Ginzburg-Landau方程吸引子的存在性;付晓玉[7]研究了Ginzburg-Landau方程的能控性;张凤[8–9]证明了非线性Ginzburg-Landau方程的拉回吸引子。他们大多都是对单个方程进行研究并得出他们的吸引子,目前涉及一类耦合Ginzburg-Landau方程组的拉回吸引子的研究很少。

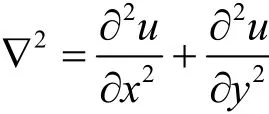
1 预备知识
本文将用到下列Banach空间记号。

本文还将用到下列定义1–定义4,详见文献[11–12]。
定义1 令X是Banach空间,距离d(⋅,⋅)=0,若一族定义于X上的双参数映射U(t,τ):X→X,t≥τ,τ∈R,满足:(1)U(t,τ)=U(t,r)U(r,τ),∀τ≤r≤t;(2)U(τ,τ)=Id,τ∈R,则称U(t,τ)是一个过程。
令P(X)表示X的所有非空子集族,且D表示X中所有非空带参数的子集组成的集合。
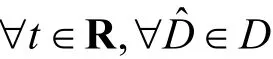
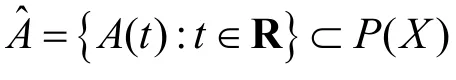

2 主要结果

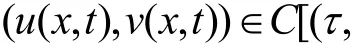
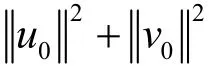

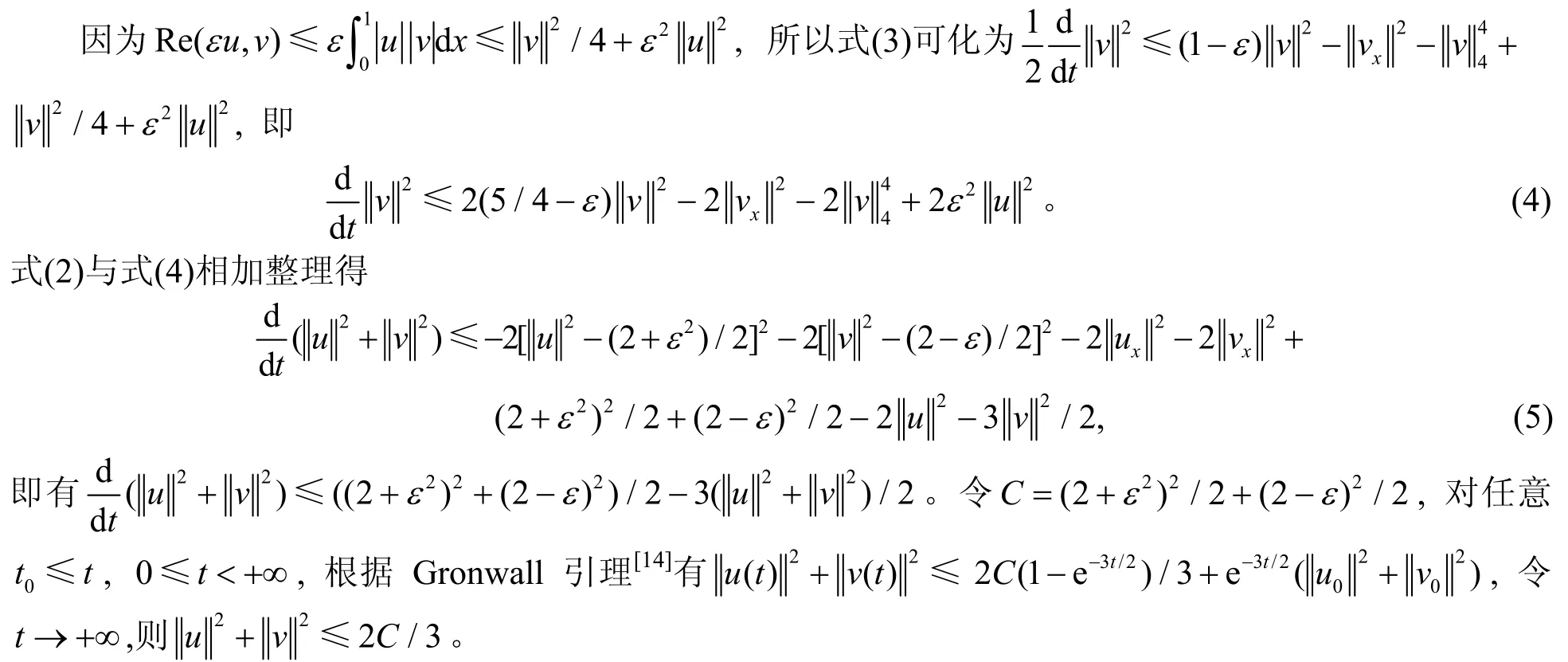
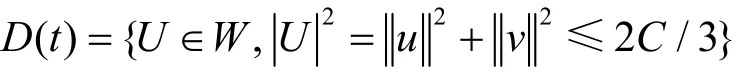

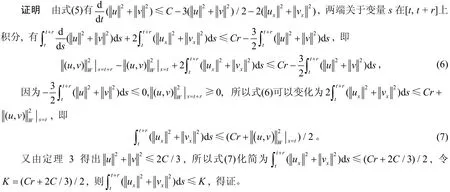
定理4 在定理3条件下,当t充分大时,那么过程U在W中存在拉回吸引子。
证明由定理3可知,过程U在W中存在一个拉回D–吸收集,只需验证满足拉回条件C即可得出该过程U在W中存在拉回吸引子。
对方程组(1)的第一个方程两边用-uxx作内积,并取实部整理得


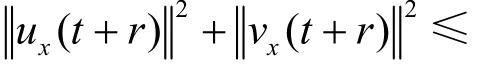
综上,由定理1,定理2和定理3以及定理4最终得出,方程组(1)存在拉回D–吸引子。
3 结论
本文借助能量方程方法,得到耦合复Ginzburg-Landau方程组在W中存在拉回吸收集,且满足拉回条件C,从而得到方程组存在拉回D–吸引子。至于该拉回吸引子是否连续、方程组是否存在随机吸引子、方程组带有随机项时是否具有随机吸引子以及该吸引子是否连续等问题有待进一步探讨。
[1] Crauel H,Flandoli F. Attractors for random dynamical systems probab [J]. Theory Related Fields,1994,100:365-393.
[2] Crauel H,Debussche A,Flandoli F. Random attractors [J]. Dynamics Differential Equations,1997,9:307-341.
[3] 陈兆蕙,杨林,李泽华. 非线性耦合Ginzburg-Landau方程组的整体吸引子[J]. 湖南文理学院学报(自然科学版),2010,22 (3):9-11.
[4] 王蕊,李扬荣. 带有可乘白噪音的广义Ginzburg-Landau方程的随机吸引子[J]. 西南大学学报(自然科学版),2014,34(2):92-95.
[5] 鲍杰,舒级. 高阶广义2D Ginzburg-Landau 方程的随机吸引子[J]. 四川师范大学学报(自然科学版),2014,37(5):298-306.
[6] 张元元,陈光淦. 带Robin边界条件的2维随机Ginzburg-Landau方程的吸引子[J]. 四川师范大学学报(自然科学版),2015,38(1):20-26.
[7] 付晓玉,柳絮,张旭. 拟现性复Ginzburg-Landau方程的能控性[J]. 中国科学:数学,2016,46(10):1 425-1 444.
[8] 张凤,姜金平,王艳,等. 非线性Ginzburg –Landau方程的拉回吸引子[J]. 曲靖师范学院学报(自然科学版),2016,35(6):7-9.
[9] 张凤,姜金平,王艳,等. 复系数Ginzburg-Landau方程的拉回吸引子[J]. 云南师范大学学报(自然科学版),2017,37(1):32–36.
[10] 高继华,史文茂,张超,等. 耦合复Ginzburg-Landau方程中的相模螺旋结构相似性[J]. 深圳大学学报(理工版),2016,33(3):272–280.
[11] Marn-Rubio P,Real J. On the relation between two different concepts of pullback attractors for non-autonomous dynamical systems [J]. Nonlinear Analysis,2009(9):3 956–3 963.
[12] Garca-Luengo J,Marn-Rubio P,Real J. Pullback attractors in V for non-autonomous 2D-Navier Stokes equations and their tempered behavior [J]. Journal of Different Equations,2012(8):4 333–4 356.
[13] 李栋龙,郭柏灵,刘旭红. 三维复Ginzburg-Landau方程的整体解的存在唯一性[J]. 高校应用数学学报,2004,19(4):409–416.
[14] Teman R. Infinite dimensional dynamical systems in mechanics and physics [J]. Berlin:Springer-Verlag,2000.
[15] 程其襄,张奠宇,魏国强,等. 实变函数与泛函分析基础[M]. 北京:高等教育出版社,2007:170–288 .
Pullback attractor for coupled complex Ginzburg-Landau Equations
Chen Zhaohui1,Wu Changjian1,Tang Yuelong2,Zhang Xinghong3
(1. Zhujiang College,South China Agricultural University,Guangzhou 510900,China;2. Mathematics and Computing Sciences,Hunan University of Science And Engineering,Yongzhou 425199,China;3. School of Automation,Beijing Institute of Technology,Beijing 100081,China)
The coupled complex Ginzburg Landau equation system for model to study the existence of pullback attractor under periodic boundary conditions and initial conditions. The method of energy equations is mainly used in this paper. First,when the closed process exists inW,and the closed process is bounded,the existence of the pull-back absorbing set is obtained. Second,when the initial and boundary condition are satisfied,the pull-back conditionCis used to prove the existence of pullback attractor for the coupled Ginzburg-Landau equations.
Coupled Ginzburg-Landau Equations;pull back conditionC;pullback attractor
O 175.29
A
1672–6146(2017)04-0004-04
10.3969/j.issn.1672–6146.2017.04.002
陈兆蕙,931832523@qq.com。
2017–09–10
广东省普通高校青年创新人才项目(2016KQNCX229);广东省“创新强项工程”专项建设项目;华农珠江学院经费资助。
(责任编校:张红)
