香丽高速富水软岩隧道拱顶支护力的上限分析

方菊明,窦友谋

(云南工程建设总承包公司,云南 昆明,650000)

香丽高速富水软岩隧道拱顶支护力的上限分析

方菊明,窦友谋

(云南工程建设总承包公司,云南 昆明,650000)

依据极限分析上限原理,基于实际工程建立了非线性破坏准则下深埋地下隧道拱顶的破坏模型。考虑到富水软岩地质,根据饱和度来选用相应的岩石强度参数,利用边界条件推导了破坏体的形状,得到了拱顶所需支护力的表达式。将理论值与香丽高速隧道监控量测值进行了对比,结果表明,二者吻合良好,体现了本文方法的正确性与可行性。

软岩;富水;极限分析理论;深埋洞室;非线性破坏准则;支护力

隧道工程施工中的稳定性问题一直是国内学者研究的热点,研究对象包括隧道掌子面、拱顶、仰拱等常见易发生失稳的地方,研究方法包括模型试验、理论分析和数值模拟计算等。Fraldi和Guarracino[1-3]在分析隧道拱顶的破坏时,依据极限分析理论,建立了曲线破坏模型,推导了拱顶潜在破坏体的形状表达式,结果直观且理论依据充分。孙谋和刘维宁[4]、杨子汉等[5]分别采用突变理论和上限原理,建立了岩溶区域隧道掘进过程中,掌子面的二维和三维破坏模型,并分析了影响防突层厚度的相关因素。李术才等[6]在研究掌子面距离前方溶洞最小安全距离时,还考虑了爆破对岩层带来的扰动以及高压岩溶水的影响。香丽高速第七项目部K56+663.04～K65+995中隧道部分,其施工的难点在于围岩条件差,且为软岩,周边地下水分布广泛,围岩极易发生大变形。本文针对这一工况,利用极限分析对富水软岩隧道拱顶的破坏进行了分析。

1 极限分析理论与破坏准则

1.1 极限分析上限原理

由Drucker等人创立的极限分析理论,为岩土工程相关研究提供了新的思路和方法。Chen[7]对极限分析的上下限定理进行了详细地介绍和分析,并将其引入土压力和边坡等算例中。通过运动上下限定理,可以列出所求解的上限和下限值,而实际的真实解则应该在这个范围之内。本文所采用的是上限原理,在使用该理论时要注意它的3个基本假设:① 理想弹塑性材料假设;② 小变形假设;③ 材料符合关联流动性法则。根据上限原理的基本方法,假设潜在破坏体沿着一条曲线发生失稳,且根据对称原则进行相应的简化,在该临界状态下许可速度场满足相应的边界条件。结合虚功(率)原理,可知内能耗散在数值上应与外力荷载的功率相等,数学表达式为

1.2 非线性Hoek-Brown破坏准则

在对岩土工程进行分析时,其特殊性在于要先确定所采用的破坏准则。以前的大量分析工作中,如陈小平、刘日成等[8-9]都采用线性Mohr-Coulomb准则,该准则形式简单,适用范围广,认为岩土体发生破坏时,主应力和切应力呈线性关系。但经大量的试验和理论验证,岩土体材料更符合非线性破坏的特性。非线性H-B破坏准则适用于深埋岩质隧道,与本文所依托的工程实例相符。因此，本文采用该准则,准则的一种表达式[10-11]为

式(2)中:τn为材料的剪应力,可通过试验或者工程经验取得;σn为材料正应力;参数A和B是无量纲常数,取值范围为0～1;σci为单轴抗压强度;σtm为抗拉强度。

1.3 饱和度对岩体强度的影响

水对岩体有软化作用,饱和岩体单轴抗压强度与岩体单轴抗压强度之比计为软化系数,当软化系数小于0.75时称该岩石为软化岩石。软岩易受到水的影响,遇水后可能发生形变,力学性能也会下降。饱和度(Sr)是衡量岩体受影响程度的参数,当饱和度趋近于临界值时,软岩强度大幅降低,可能造成结构失稳破坏。Vásárhelyi等[12]给出了饱和度与岩体强度关系的最佳拟合公式:

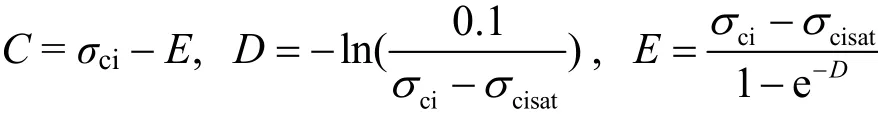
2 富水软岩隧道拱顶破坏分析

2.1 破坏模式

利用极限分析的基本原理,研究拱顶发生整体式的破坏,破坏体的边界是一条曲线。基于H-B破坏准则,并根据对称原则进行简化,建立拱顶破坏模型如图1所示。为计算简便,将隧道断面简化为矩形来分析。图1中:L为隧道净宽的一半;q为拱顶所需支护力;H为塌落体的高度。

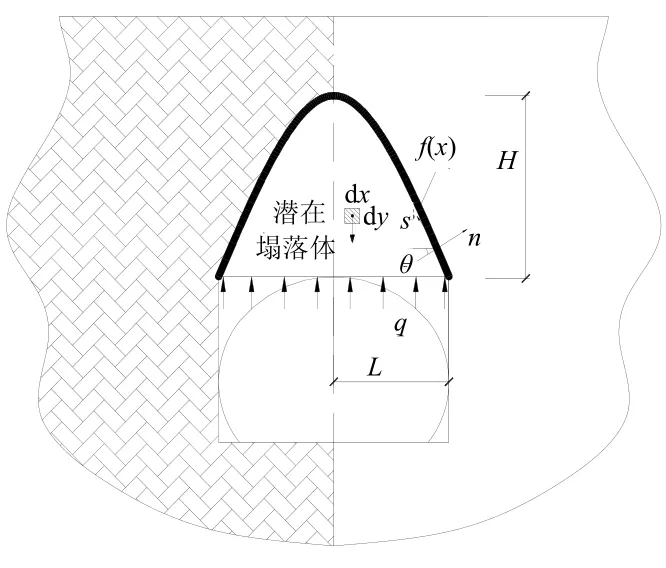
图1 隧道拱顶破坏模型

2.2 计算过程

首先根据弹塑性相关原理,得到正应变和切应变的表达式

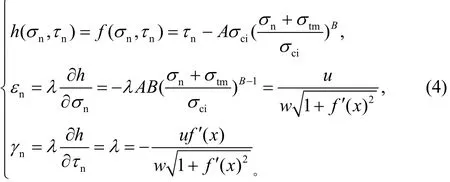
通过迭代变换,消去式(4)中的λ和w,得到分离曲线上任意一点的应力表达式,从而得到任意一点应变能的表达式

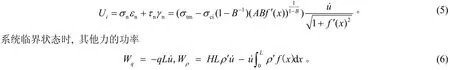
式(6)中:q表示拱顶支护力;ρ′表示围岩容重;为极限状态下的虚功率。

联立式(1)、式(5)、式(6),可得

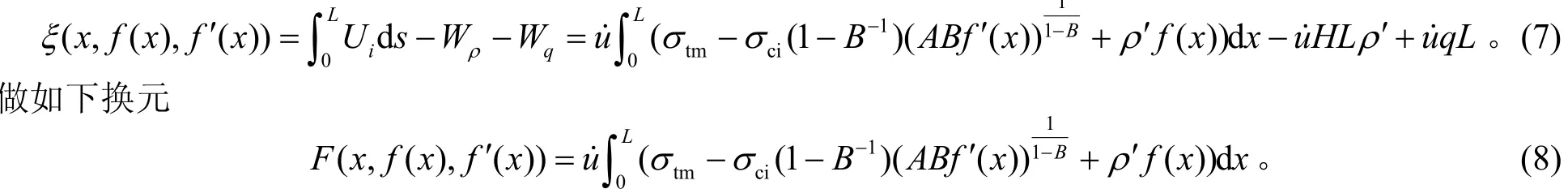
式(7)的极值完全由F决定,而F是一个包含变量f(x)的函数,因此将泛函的极值问题进行转换,利用欧拉方程

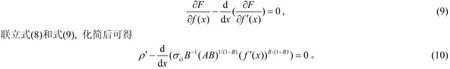
式(10)为一个常系数微分方程,积分可求得分离曲线的表达式

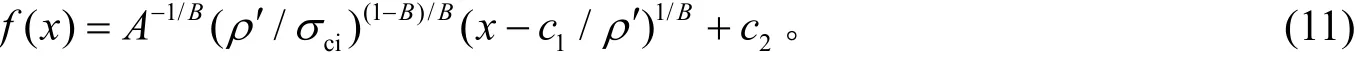
其中,c1和c2是积分常数,可以由几何条件和边界条件来确定。从图1可知f(x=0)=-H,f(x=L)=0,τ(x=0,y=-H)=0。其中,τ为剪应力。将边界条件代入式(11)可得

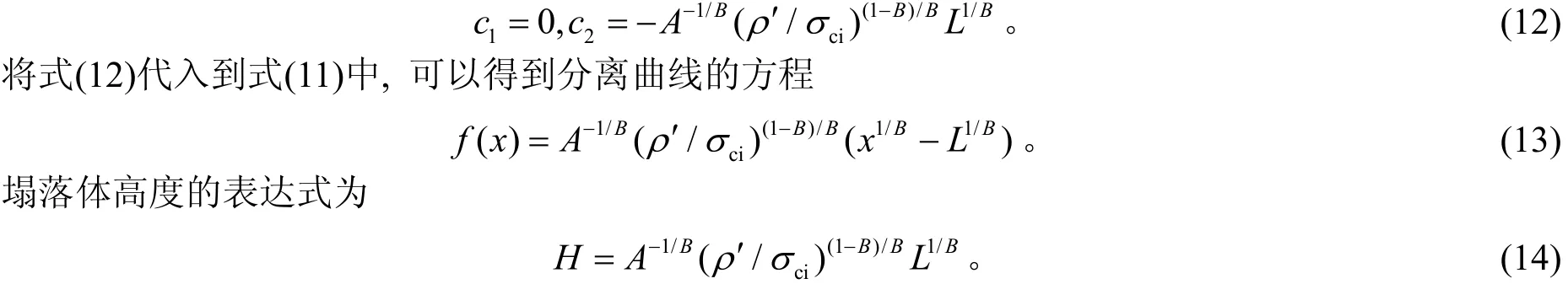
根据虚功原理,将式(13)、(14)代入式(7)中可以求得拱顶所需要支护力的表达式q=ρ′H+(1/(1+B)-2B-1)A-1/Bσ(ρ′/σ)1/BL1/B。由于软岩受到水作用后,强度会受到影响,因此应根据饱和度,用σci(Sr)代替σci进行计算。

3 工程实例对比与分析

香丽高速隧道均为强-中风化板岩,遇水软化后均有可能产生大变形。测区内地下水发育,开挖后可能造成隧道底部隆起,仰拱破坏,周边挤入,初期支护破坏,造成坍塌,引发安全和质量事故。因此,做好监控量测工作,控制好围岩大变形是本工程隧道施工中的重点。由于本工程的特殊性,除了常规的隧道监控量测项目,还在几个断面布置了土压力盒、钢筋应变计等仪器。通过监控围岩、初期支护的应力应变,判断结构的稳定性,并为施做二衬的时机提供参考,现场监测情况如图2所示。

图2 土压力盒的安装

通过长期的监控量测,得到拱顶土压力盒参数如表1所示。将相关参数代入前面的相应公式中,比较计算值与实际值,判断围岩的稳定情况,并验证理论的准确性。

表1 隧道开挖后所需支护力

图3为支护力上限解与监控量测值的比较。从图3可以看出,围岩压力会随着隧道开挖后的时间逐渐增长,开始增长较快,渐渐放缓,并接近于理论的极限值。应用上限定理求得的上限解必定不小于实际破坏的荷载值。当实际值接近于上限值时,应当同步加密围岩变形、收敛的监测,尽早制定处理方案及施做二衬。

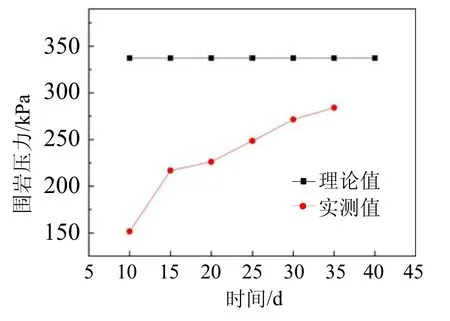
图3 K33+400处围岩压力大小

4 结论

本文通过上限分析原理,构建了非线性准则下深埋隧道拱顶破坏塌落模型。通过参数比较分析,得到结论如下:(1) 隧道开挖后,拱顶会缓慢变形释放应力,当速度场和应力场处于某一个临界状态时,拱顶可能发生整体式的失稳破坏;(2) 推导了塌落体破坏的形状分离曲线,得到了所需支护力的表达式,由于围岩为软岩,遇水可能发生大变形,因此应根据饱和度采用不同的单轴抗压强度来计算防止塌落体破坏所需的支护力。(3) 根据香丽高速隧道段的相关地质资料,计算了富水软岩地质条件下,拱顶支护力的上限值,并与实际监测值进行了比较。结果表明,拱顶土压力随着开挖后的时间增大而变大,并逐步趋近于理论值。

[1] Fraldi M,Guarracino F. Limit analysis of collapse mechanisms in cavities and tunnels according to the Hoek-Brown failure criterion [J]. International Journal of Rock Mechanics &Mining Sciences,2009,46(4):665-673.

[2] Fraldi M,Guarracino F. Analytical solutions for collapse mechanisms in tunnels with arbitrary cross sections [J].International Journal of Solids and Structures,2010,47(2):216-223.

[3] Fraldi M,Guarracino F. Evaluation of impending collapse in circular tunnels by analytical and numerical approaches [J].Tunnelling and Underground Space Technology,2011,26(4):507-516.

[4] 孙谋,刘维宁. 高风险岩溶隧道掌子面突水机制研究[J]. 岩土力学,2011,32(4):1 175-1 180.

[5] 杨子汉,杨小礼,许敬叔,等. 基于上限原理的两种岩溶隧道岩墙厚度计算方法[J]. 岩土力学,2017,38(3):801-809.

[6] 李术才,袁永才,李利平,等. 钻爆施工条件下岩溶隧道掌子面突水机制及最小安全厚度研究[J]. 岩土工程学报,2015,37(2):313-320.

[7] Chen W F. Limit analysis and soil plasticity [M]. Amsterdam:Elsevier Science,1975:235-238.

[8] 陈小平. 基于摩尔库伦准则的岩石地基极限承载力研究[J]. 地下空间与工程学报,2016,12(S1):95-99.

[9] 刘日成,张芹,王育奎,等. 复合土钉墙支护效果数值模拟[J]. 地下空间与工程学报,2012,8(01):182-189.

[10] Yang Zi-han,Zhang Jia-hua. Minimum safe thickness of rock plug inkarst tunnel according to upper bound theorem [J]. Journal of Central South University,2016,23(9):2 346-2 353.

[11] YANG Xiao-li,LI Wen-tao,PAN Qiu-jing. Influences of anisotropy and inhomogeneity on supporting pressure of tunnel face with kinematical approach [J]. Journal of Central South University,2015,22(9):3 536–3 543.

[12] Vásárhelyi B,Ván P. Influence of water content on the strength of rock [J]. Engineering Geology,2006,84(1/2):70-74.

Upper bound solutions of supporting force of tunnel vault in water-rich soft rock

Fang Juming,Dou Youmou
(Yunnan Engineering Construction Co Ltd,Kunming 650000,China)

According to the upper bound theorem,a reliable failure pattern based on Hoek-Brown failure criterion is established,and in consideration of soft rock,different rock parameter is adopted based on different saturations. By using the boundary conditions,the functions of detaching curve and the supporting pressure are derived. At last,the supporting force of Apuluo tunnel in Li-xiang highway is calculated in this method and the results is compared with the monitoring data,which shows the validity of this way.

soft rock;water-rich;limit analysis theory;deep cavity;nonlinear failure criterion;supporting force

TU 45

A

1672–6146(2017)04–0085–04

10.3969/j.issn.1672–6146.2017.04.021

方菊明,11321931217@qq.com。

2017–09–10

香丽高速项目(2017-315(3186))。

(责任编校:张红)