关于不定方程x2+64=4yn(n=5,9)的解

尚旭

(浙江师范大学 数理与信息工程学院,浙江 金华,321004)

关于不定方程x2+64=4yn(n=5,9)的解

尚旭

(浙江师范大学 数理与信息工程学院,浙江 金华,321004)

利用代数数论整数环的唯一分解性,研究了不定方程x2+64=4yn(n=5,9)的整数解问题,并证明了当n=5时,该方程仅有整数解(x,y)=(±8,2);当n=9时,该方程无整数解。

不定方程;整数解;代数数论

不定方程[1]是指解的范围为整数、正整数、有理数或代数整数的方程或方程组,其未知数的个数通常多于方程的个数。不定方程与数学的其他分支,如代数数论、代数几何、组合数学等有着紧密的联系,在有限群论和最优设计中也常常提出不定方程解的问题。关于不定方程还有许多未知领域尚未研究,比如对于多元高次的不定方程研究较少。设A、B∈N,A无平方因子,关于不定方程Ax2+B=Cyn,(x,y,n∈N,n≥2)解的问题是数论中的一个重要问题。近年来,研究者研究了许多形式的不定方程,得到了许多重要的结论。当A=1,B=1,C=1时,Ledesgue[2]证明了无整数解;Nagell[3]证明了当A=2,B=1,C=1,n=5时仅有整数解(x,y)=(±11,3);孙树东[4]证明了A=1,B=64,C=1,n=13时无整数解;张四保[5]证明了A=1,B=64,C=4,n=13时无整数解;李中恢等[6]证明了A=1,B=16,C=1,n=11时无整数解;张杰[7]证明了A=1,B=64,C=1,n=7时仅有整数解(x,y)=(±8,2);高媛媛等[8]证明了A=1,B=64,C=1,n=5时无整数解;冉银霞[9]证明了A=1,B=44,C=1,n=7时无整数解;何桃等[10]等证明了A=1,B=4,C=1,n=7时无整数解;高丽等[11]证明了A=1,B=16,C=1,n=7时无整数解;杨全[12]证明了A=1,B=16,C=1,n=13时无整数解;安晓峰[13]证明了当A=1,B=64,C=1,n=11时无整数解;廖江东等[14]证明了A=1,B=16,C=1,n=3时无整数解。而对于A=1,B=64,C=4时未曾研究,基于此,本文研究当A=1,B=64,C=4,n=5,9时方程(1)的整数解问题。

1 引理

引理1[15]设M是惟一分解整数环,正整数k≥2,以及α,β∈ Z,(α,β)=1,若αβ=γk,γ∈M,则有α=ε1μk,β=ε2νk,μ,ν∈M,其中ε1,ε2是M的单位元素,并且ε1ε2=εk,ε为单位元素。

2 定理及证明

定理1 不定方程

仅有整数解(x,y)=(±8,2)。

证明:分2种情况说明。①x≡1(mod2),则在Ζ[i]中,式(1)可以等价(x+ 8i)(x- 8i)=4y5,x,y∈Ζ。设(x+ 8i)(x- 8i)=η。由η|(2x,16i)=2,得η只能取1,1+i,2。因x≡1(mod2)有x+ 8i≡1(mod2),所以η≠ 2。假如η=1+i,则N(1+i)|N(x+ 8i),即2|x2+64。然而这与x≡1(mod2)矛盾,所以η=1。由引理1有x+ 8i=4(a+bi)5,x,a,b∈Ζ,因此得

由式(3)有b=±1,±2。当b=1时,由式(3)得8=4(5a4-10a2+1),1=5(a4-2a2),该式要成立,则需5|1,然而不可能,所以b=1不成立。当b=-1时,由式(3)得8=-4(5a4-10a2+1)-3=5(a4-2a2),该式要成立,则需5|-3,然而不可能,所以b=-1不成立。当b=2时,由式(3)得-3=a2(a2-8),该式要成立,则a2=1。代入上式右边得a2(a2-8)=-7 ≠-3,所以b=2不成立。当b=-2时,由式(3)得8=-8(5a4-40a2+ 16)-17=5(a4-8a2),该式要成立,需5|-17,然而不可能,因此b=-2不成立。因此当x≡1(mod2)时,不定方程x2+64=4y5无整数解。

② 当x≡0(mod2)时,易知x为偶数,设x=2x1,x1∈Ζ。代入式(1)得

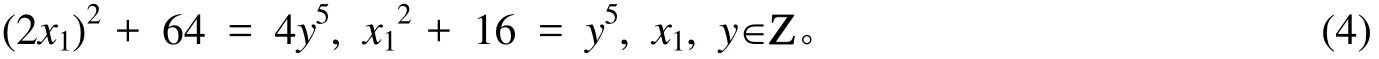
接下来讨论不定方程x12+16=y5,x1,y∈Ζ的解。分2种情况讨论。

(i)x1≡1(mod2)时,则在Ζ[i]中,式(4)可以等价(x1+4i)(x1-4i)=y5,x,y∈Ζ。设(x1+4i)(x1-4i)=η,由η|(2x1,8i)=2,得η只能取1,1+i,2。因x1≡1(mod2)有x1+4i ≡ 1(mod2),所以η≠ 2。假如η=1+i,则N(1+i)|N(x1+4i),即2|x12+16。这与x1≡1(mod2)产生矛盾,所以η=1。由引理1有x1+4i =(a+bi)5,x1,a,b∈Ζ,因此得

由式(6)有b=±1,±2,±4。当b=1时,由式(6)得4=5a4-10a2+1,3=5(a4-2a2),该式要成立,需5|3,然而不可能,所以b=1不成立。当b=-1时,由式(6)得-4=5a4-10a2+1,-1=a2(a2-2),该式要成立,则a2=1。代入上式右边得a2(a2-2)=-1,满足,则将a2=1,b=-1代入式(6),解得x1=±4。然而与x1≡ 1(mod2)矛盾,故不成立。当b=2时,由式(6)得4=2(5a4-40a2+16),-14=5(a4-8a2),该式要成立,需5|-14,然而不可能,所以b=2不成立。当b=-2时,由式(6)得4=-2(5a4-40a2+16),- 18=5(a4-8a2),该式要成立,需5|-18,然而不可能,所以当b=-2时不定方程不成立。

由上述证明可知,当b=±4时不定方程不成立。所以当x1≡1(mod2)时,不定方程x12+16=y15无整数解。

(ii) 当x1≡0(mod2)时,易知x1为偶数,y也是偶数,设x1=2x2,y=2y1,x2,y1∈Z。代入式(1)得

易知x2为偶数,令x2=2x3,x3∈Ζ,代入式(7)得

易知x3为奇数,只需讨论x32+1=2y15的整数解。在Ζ[i]中,式(8)可以等价(x3+i)(x3-i)=i(1-i)2y15。记β=(x3+i,x3-i),有β|(2x3,2i)=2,所以β只能取1,1-i,2。显然β≠ 2,因为x/2+yi/2∉Z[i],若β=1,则i(1-i)2=2一定只能整除x3+i,x3-i中的一个,但这是不可能的,故β=1-i。由此可以得到(x3+i) (x3-i)/((1+i) (1-i))=y15,((x3+i)/(1+i),(x3-i)/ (1-i))=1。故由引理1可得x3+i=(1-i)(a+bi)5,x3,a,b∈ Ζ。x3=a5-5a4b- 10a3b2+10a2b3+5ab4-b5。 1=a5+5a4b- 10a3b2-10a2b3+5ab4+b5,1=(a+b)(a4+4a3b- 14a2b2+4ab3+b4),则a+b=±1或a4+4a3b- 14a2b2+4ab3+b4=±1。

下面讨论何种情况成立。a4+4a3b- 14a2b2+4ab3+b4=±1,a4+4a3b- 14a2b2+4ab3+b4=(a+b)4-20a2b2=±1,由此得到-20a2b2=0或-2。而-20a2b2=-2,不可能,所以a+b=1,ab=0,由此得a=1,b=0或a=0,b=1,代入x3=a5-5a4b- 10a3b2+10a2b3+5ab4-b5中得x3=±1,将x3=±1代入(8)中得y1=1。所以不定方程x2+64=4y5的整数解为(x,y)=(±8,2)。

定理2 不定方程

无整数解。

证明:分2种情况说明。①x≡1(mod2),则在Ζ[i]中,式(9)可以等价写成(x+ 8i)(x- 8i)=4y9,x,y∈Ζ。设(x+ 8i)(x- 8i)=η,由η|(2x,16i)=2,得η只能取1,1+i,2。因x≡1(mod2)有x+ 8i≡1(mod2),所以η≠ 2。假如η=1+i,则N(1+i)|N(x+ 8i),即2|x2+64。然而这就与x≡1(mod2)矛盾,所以η=1。由此及引理1有x+ 8i =4(a+bi)9,x,a,b∈Ζ,因此得

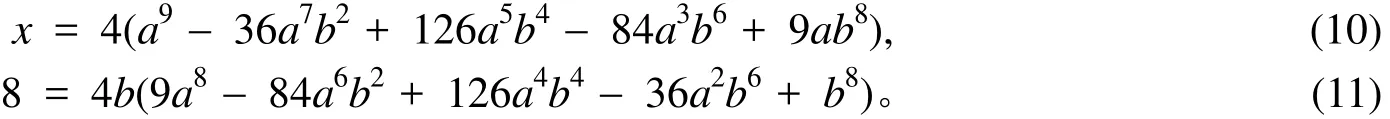
由式(11)有b=±1,±2。当b=1时,得8=4(9a8-84a6+126a4-36a2+1),1=3(3a8-28a6+42a4-12a2),该式要成立,需3|1,然而不可能,所以b=1不成立。当b=-1时,由式(11)得8=-4(9a8-84a6+126a4- 36a2+1),-1=a2(3a6-28a4+42a2-12),该式要成立,则a2=1。代入a2(3a6-28a4+42a2-12)=5 ≠-1,所以b=-1不成立。当b=2时,由式(11)得8=8(9a8-336a6+2016a4-2304a2+256),-85=-5×17=a2(3a6-112a4+672a2-768),该式要成立,则a2=1。将a2=1代入式(11)中得a2(3a6-112a4+672a2-768)=-205 ≠-85,所以b=2不成立。当b=-2时,由式(11)得8=-8(9a8-336a6+2016a4-2304a2+256),-257=(3a8-112a6+72a4-768a2),该式要成立,需3|-257,然而不可能,因此b=-2不成立。因此当x≡1(mod2)时,不定方程x2+64=4y9无整数解。

② 当x≡0(mod2)时,易知x为偶数,设x=2x1,x1∈Ζ。代入式(9)得(2x1)2+64=4y9,x12+16=y9,x1,y∈Ζ。不定方程x2+16=y9无整数解[16]已被证明,因此当x≡0(mod2)时,不定方程x2+64=4y9无整数解。

综上所述:不定方程x2+64=4y9,x,y∈Ζ无整数解。

[1] 柯召,孙琦. 谈谈不定方程[M]. 哈尔滨:哈尔滨工业大学出版社,2011:1-2.

[2] Lebesgue V A. Surlimpossibilite ennumbers entiers de equationxm=y2+1 [J]. Nouvelle Annals of Mathematics,1850,9(1):178–181.

[3] Nagell T. Surlimpossibilite de quelques equations deux indeterminees [J]. Norsk Marem Fornmings Skrefter Senel,1921,13(1):65–82.

[4] 孙树东. 不定方程x2+64=y13的整数解[J]. 吉林师范大学学报(自然科学版),2015,35(3):78–80.

[5] 张四保,吕明富. 关于不定方程x2+64=4y13的解[J]. 喀什师范学院学报,2010,31(3):22–23.

[6] 李中恢,张四保. 关于不定方程x2+16=y11的解[J]. 海南大学学报(自然科学版),2009,27(3):216–218.

[7] 张杰. 关于不定方程x2+64=y7的解的讨论[J]. 重庆工商大学学报(自然科学版),2012,29(3):27–28.

[8] 高媛媛,郭金保. 关于不定方程x2+64=y5[J]. 延安大学学报(自然科学版),2010,29(1):6–7.

[9] 冉银霞. 关于不定方程x2+44=y7[J]. 延安大学学报(自然科学版),2012,31(4):14–15

[10] 何桃,郭金保,穆秀梅,等. 关于不定方程x2+4=y7[J]. 延安大学学报(自然科学版),2011,30(3):7–8.

[11] 高丽,马永刚. 关于不定方程x2+16=y7的解的讨论[J]. 西南民族大学学报(自然科学版),2008,34(1):27–29.

[12] 杨全. 关于不定方程x2+16=y13的解[J]. 海南大学学报自然科学版,2012,30(4):306–308.

[13] 安晓峰. 关于不定方程x2+64=y11的解的讨论[J]. 重庆工商大学学报(自然科学版),2014,31(10):16–17.

[14] 廖江东,柳杨. 关于不定方程x2+16=y3[J]. 四川理工学院学报(自然科学版),2007,20(2):4–5.

[15] 潘承洞,潘承彪. 代数数论[M]. 2版. 哈尔滨:哈尔滨工业大学出版社,2014:105–106.

[16] 杨全. 关于不定方程x2+16=y9的解[J]. 牡丹江大学学报,2013,22(8):119–120.

The solution on Diophantine equationx2+64=4yn(n=5,9)

Shang Xu
(College of Mathematics and Information Engineering,Zhejiang Normal University,Jinhua Zhejiang 321004,China)

The problem of integer solution to the Diophantine equationx2+64=4yn(n=5,9) is discussed by using the methods of algebraic number theory. The Diophantine equation has integer solution(x,y)=(±8,2) whenn=5,and the Diophantine equation has no integer solution whenn=9.

Diophantine equation;integer solution;algebraic number theory

O 156.2

A

1672–6146(2017)04–0001–03

10.3969/j.issn.1672–6146.2017.04.001

尚旭,sxzjshdx@163.com。

2017–04–10

国家自然科学基金(11171137)。

(责任编校:刘刚毅)