拉普拉斯变换求解转动参考系下的真实自由落体

陆 林，孙 斌*，杨友昌

（遵义师范学院物理与电子科学学院，贵州遵义563006）

自由落体是最常见的一种运动，在大学物理教材[1]及文献[2]中只单独讨论了地球自转的影响或空气阻力的影响，这不利于学生正确认识真实的自由落体运动。文献[3]虽同时考虑了两者的影响，但微分方程组的求解方法过于复杂[2,4-6]，不便于学生理解。《理论力学》教材[1]及文献[6]舍去了二阶无穷小量或运用了拉格朗日常数变易法来求解，同时受坐标原点选取的影响，使得求解过程更为复杂，可操作性差，因此寻找更简便的办法来求解此类微分方程组是本文的目的之一。作者通过拉普拉斯变换，将复杂的微分方程组变换为简单的代数方程组，保留了二阶无穷小量（），减少了方程求解所需的初始条件，并且不必考虑坐标原点选取的影响，解此微分方程组，给出了完整的自由落体运动的物理图像。

1 自由落体运动微分方程组的建立

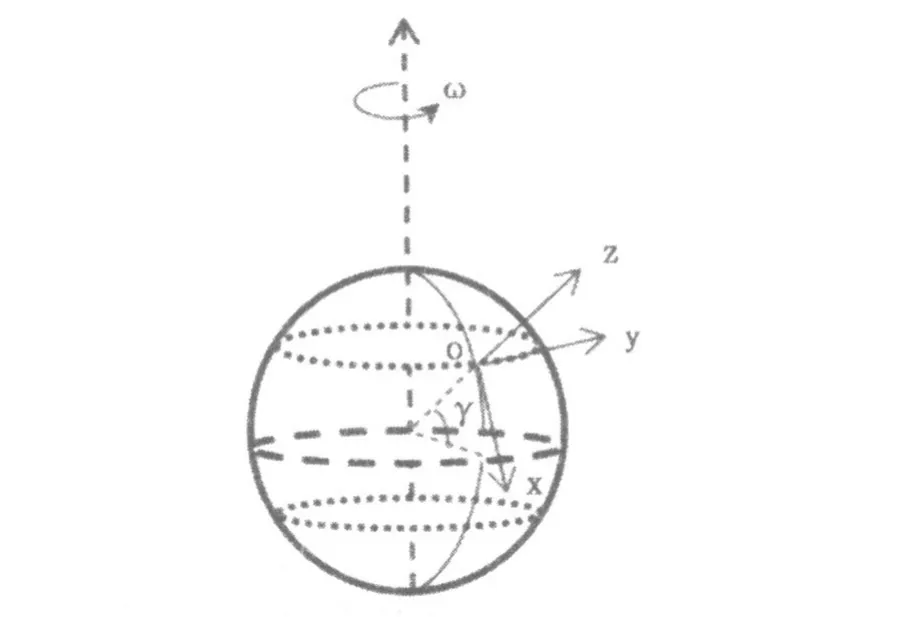
图1 自由落体运动坐标系统示意图

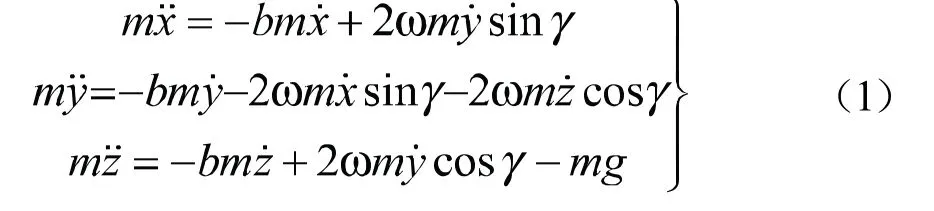
2 自由落体运动微分方程组的求解

此方程组最高阶是二阶，求解时由于受坐标系原点及初始条件的影响，方程难以求解。利用位置矢量和动量关系，可以将此方程组降为一阶，即：

接下来采用拉普拉斯变换法求解。运用拉普拉斯变换法求解（1）式是直接对坐标求解，首先要假设坐标原点。当运用动量表达式后，（1）式变为（2）式，即一阶微分方程，此时无需假设坐标原点，只需假设初始动量值即可求出方程的解。

对方程组（4）进行拉普拉斯反演变换，可得到方程组（2）的解：

（5）式除以质量m，便可得各方向上的速度：

对（6）式积分即得真实高空自由落体在各方向上的运动方程（即方程组（1）的解）：

3 结果分析

上述求解得出的运动方程表达式较复杂，很难看清楚影响自由落体运动的主要因素有哪些。因此，对运动方程做泰勒展开得：

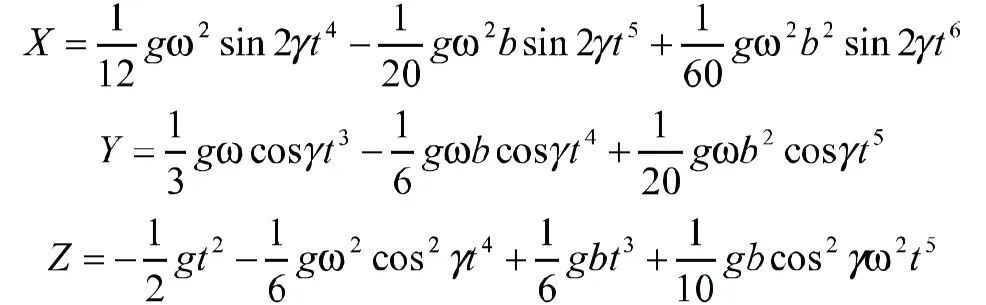
为了更加直观地认识真实的自由落体，代入实际数值：地球自转角速度，空气阻力系数b＝8.5×10-5，质点所处北纬对应的角度下落所用时间，所得运动轨迹如图2所示。

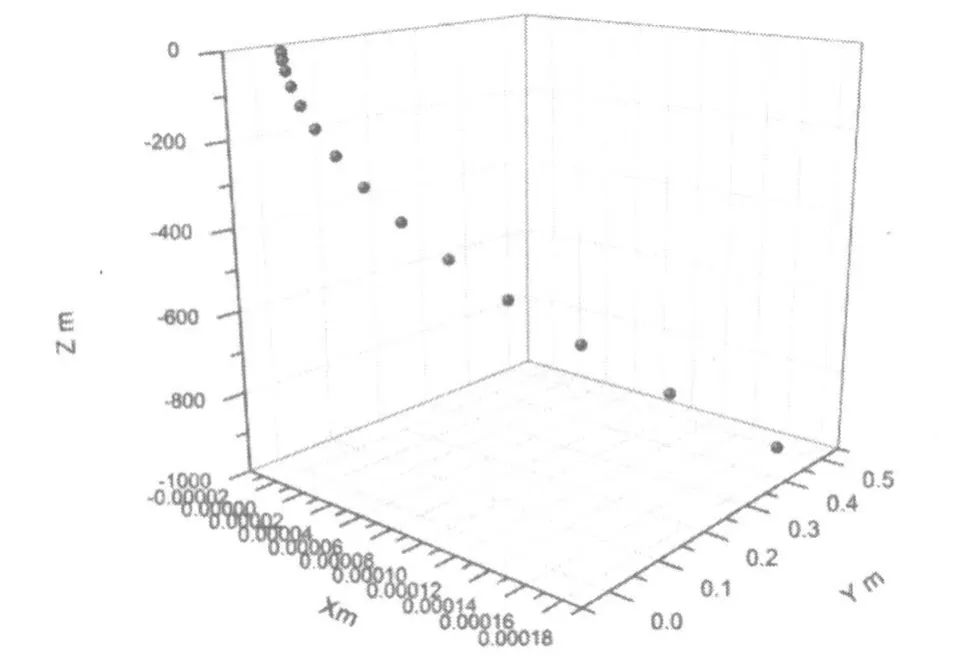
图2 自由下落小球真实的轨迹

图2画出了三维直观运动轨迹图（为了和观察保持一致，故将z轴取负），而在其他的文献[7]中虽画出了南北（x）或东西（y）方向上的运动轨迹图，但不便于学生理解。由图2可知自由落体运动曲线是一条空间抛物线，自由落体不仅仅在竖直方向上有位移，实际上在南北与东西方向上均有位移，并且随着下落高度的增加而增加，但位移量都很少，例如在x方向10-4m、在y方向为10-1m的量级。由图2也可知这个高度一般在1千米级别，而日常的自由落体基本上都是这个高度或更少，因此南北与东西方向上的位移一般可以忽略不计，因此人们往往认为自由落体运动是直线运动。

4 结论

本文在三维转动参考系下，基于牛顿定律建立了三个方程构成的二阶线性微分方程组，首先将二阶微分方程组转化为用动量表达的一阶线性微分方程组，然后运用拉普拉斯变换将动量一阶微分方程组转换为简单的代数方程组求解，并通过拉普拉斯反演变换即可求得各个方向上的动量，最后通过积分方法即可得到真实自由落体在各个方向上的运动方程；在求解过程中，采用动量形式是降阶的过程，由于采用动量作为中间变量，求解时只需要考虑初始速度而与坐标原点的选取无关。拉普拉斯变换方法对一阶微分方程求解很高效，即可避免复杂的矩阵运算又无需舍去二阶无穷小量，从而大大简化了计算过程。真实自由落体运动表达式在一定条件下可转换为理想的自由落体运动表达式，运动方程作图显示其轨迹是一条抛物线。以上求解方法也可以推广到求解其他具有初始速度的落体运动。本工作提供了一种简便、适应范围广的求解二阶线性微分方程组的方法，且有助于学生更直观地认识高空真实的自由落体运动。

[1]周衍柏.理论力学教程(第三版)[M].北京:高等教育出版社,2009.180-193.

[2]周永平,刘孜杰.北半球自由落体南偏的一种精确解法[J].大学物理,1994,13(6):l-4.

[3]楼智美.空气阻力影响北半球自由落体的偏离[J].力学与实践,2001,23(2):68-69.

[4]田慧竹,宋从芝.利用拉普拉斯变换求解微分方程[J].高等数学研究,2012,15(1):67-68.

[5]同济大学数学系.线性代数(第六版)[M].北京:高等教育出版社,2014.44-52.

[6]王立华.空气阻力对自由落体运动的影响[J].沧州师范专科学校学报,2000,16(2):50-52.

[7]孙梅娟,韩修林.空气阻力与地球自转影响下自由落体的运动[J].宿州学院学报,2010,25(8):10-12.