从Bloch空间到加权型空间上二阶微分算子与加权复合算子的积

曹成堂

（贵州工业职业技术学院，贵州贵阳550008）

文献[1]研究了复合算子；文献[2]研究了复合算子与一阶微分算子的乘积；文献[3,4]研究了一阶微分算子与其它算子的乘积；文献[2]研究了微分算子与复合算子的乘积，文献[5]研究了Bloch空间，文献[6,7]研究了Bloch型空间。受上述文献启发，本文讨论了二阶微分算子与加权复合算子的积：

1 预备引理

由Montel定理及紧算子定义，可得出下面的引理。

2 主要定理及证明

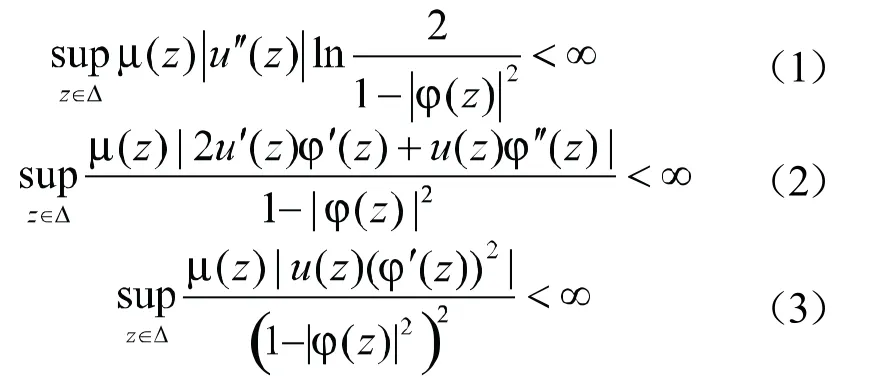
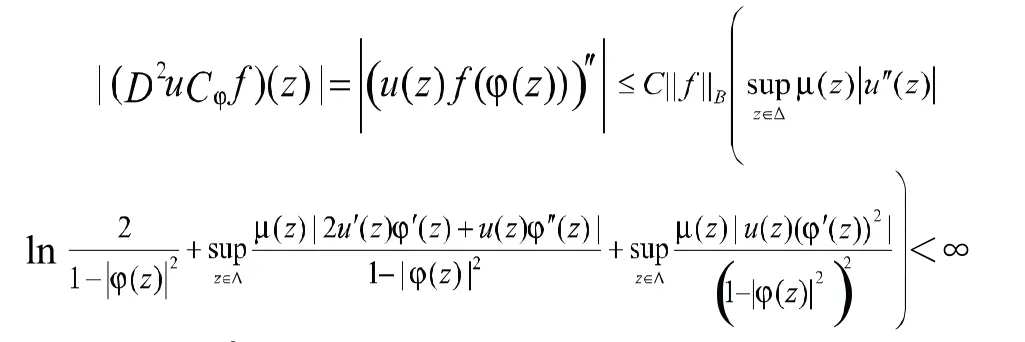
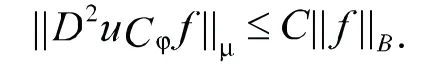
取检验函数

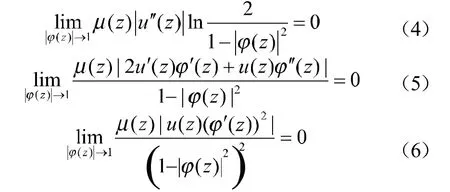
由（7）～（12）可知，当 i＞ i0时有

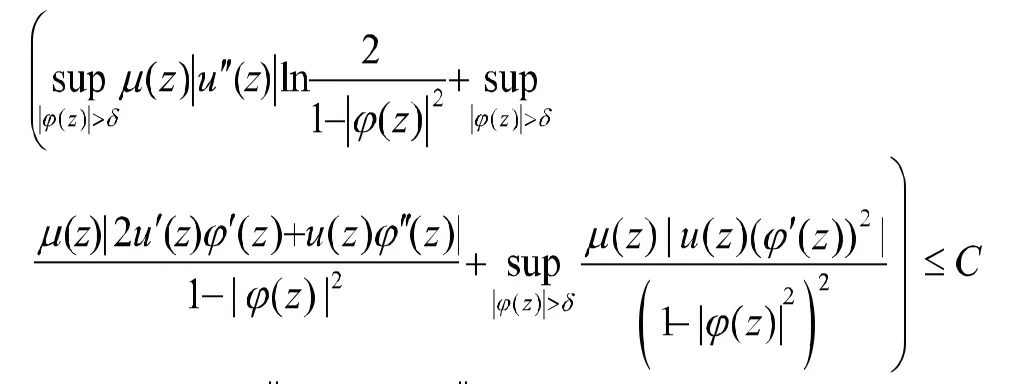
i在的任一紧子集上一致收敛于0，由引理2可得，于是，在上式两边令，可得所以（5）成立。取检验函数，同理可得（4）（6）两式成立。

[1]Zhao Ruhan.Composition operators from Bloch type spaces to Hardy and Besov spaces[J].Journal of Mathematics Analysis and Application,1999,233(2):749-766.

[2]Stevi S.Composition by followed by differentiation from and Bloch spaces to nth weight-type spaces on the unit disk[J].Applied Mathematics and computation,2010,216(12):3450-3458.

[3]刘晓曼,于燕燕.从到Zygmund空间微分算子与乘子的积[J].徐州师范大学学报(自然科学版),2011,(1):37-39.

[4]于燕燕,刘永民.从混合模空间到Bloch-型空间微分算子与乘子的积[J].数学物理学报,2012,32A(1):68-79.

[5]Zhu K H.Bloch type spaces of analytic functions[J].Rocky Mountain J Math,1993,23(3):1143-1177.

[6]张超.单位球上加权Bergman-Nevanlinna空间到Bloch-型空间上乘法,复合,微分算子的乘积[J].纯粹数学与应用数学,2016,32(3):271-287.

[7]王艳永,商庆宝.从H～∞空间到B(B_0)空间的算子T_(,)的有界性和紧性[J].江苏师范大学学报(自然科学版),2016,34(2):21-24.