传热学教学中数学基础薄弱问题与对策研究
2018-01-04姚森徐桂转胡建军王伟荆艳艳
姚森 徐桂转 胡建军 王伟 荆艳艳


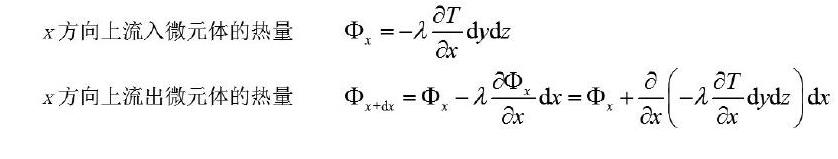
【摘 要】高等数学是各高校理工科专业必修的基础性课程。传热学是能源类专业的专业基础课之一,传热问题的分析和应用涉及大量的数学知识。在传热学教学过程中,经常存在由于学生数学基础知识薄弱,对概念和公式只能机械记忆,在分析时只能硬搬已有公式,不能清晰明确的给出计算步骤和方法。因此,在传热学教学中适当加入高等数学中相关知识点的回顾和总结,以期提高学生学习兴趣及传热学的整体教学效果。
【关键词】传热学;高等数学;计算方法
中图分类号: G642;TK124-4 文献标识码: A 文章编号: 2095-2457(2018)25-0100-002
DOI:10.19694/j.cnki.issn2095-2457.2018.25.044
【Abstract】Higher mathematics is a compulsory basic course for majors of science and engineering in universities. Heat transfer is one of the basic courses for energy majors, the analysis and application of heat transfer problems involve a large number of mathematical knowledge. In the process of heat transfer teaching, several students who have weak basic knowledge of mathematics not only memorize the concepts and formulas mechanically, but also can not give clear calculation steps and methods when analyzing actual problems. Therefore, the review and summary of relevant knowledge points in higher mathematics should be properly added to the teaching of heat transfer in order to improve students interest in learning and improve the overall teaching effect of heat transfer.
【Key words】Heat transfer; Advanced mathematics; Computational method
传热学是能源与动力工程、建筑环境与能源应用工程等本科能源类专业的专业基础课之一,传热问题的分析和应用涉及大量的高数知识,且具有计算量大、难度大等特点。高等数学是各高校理工科专业必修的基础性课程,对学生思维能力的培养和后续专业性课程的学习有着至关重要的意义。在传热学教学过程中,经常存在由于学生数学基础知识薄弱,在学习传热学基础知识时,对概念和公式只能机械式的记忆,不能合理的结合高等数学知识对其进行推倒;在分析和计算时只能硬搬已有公式,不能清晰明确的给出计算步骤和方法。因此,针对传热学中涉及到的典型的数学基础问题,本文进行了归纳和整理,为学生的传热学课程学习提供参考。
1 泰勒公式
泰勒级数的展开在物理方程推导和数值解法有着大量的应用。在建立传热问题数学物理方程时的一贯做法是,取对象的微元体,基于热力学能量守恒定律等基本定律建立微元体的能量方程。以直角坐标系下的导热微分方程的推导为例,从导热体取出任意微元体,在推导单一方向的上流入和流出微元体的热量时,表达式如下:
其中,流出微元体的熱量Φx+dx的导出就是基于泰勒公式所得。泰勒公式是一个用函数在某个点上的信息描述该点附近取值的公式,若函数f(x)在包含x0的某个闭区间[a,b]上具有n阶导数,且在开区间(a,b)上具有(n+1)阶导数,则对闭区间[a,b]上任意一点x,有下式[1]
对于x附近的x+dx,取一阶时该式可近似表达为:
f(x+dx)=f(x)+f'(x)(x-x0)
此即为各方向流出微元体的热量表达式导出的基础,若学生不能理解,则对导热微分方程掌握,尤其是圆柱坐标和球坐标下的导热微分方程,只能使用死记硬背的方式进行。
除导热微分方程外,泰勒公式在传热问题的其他控制方程推导,以及数值解法的离散方程建立过程中也有大量的应用,在此不再赘述。 在讲述相关内容时,应注重引导学生对高等数学相关内容的回顾。
2 柱坐标和球坐标的梯度
传热学研究是通过获得系统内各点的温度分布进行的。温度场是典型的数量场,通过在空间中引入坐标系,其空间点的位置可由引入的坐标系确定,当给定了温度场后,其温度可以表示为空间坐标的函数。在传热学课程教学过程中,大量使用到温度梯度的知识,如傅里叶导热定律的一般形式数学表达式为=-λgradt=-λ?塄t[2];此外,在导热微分方程和能量方程中,当物性为常数时也会出现梯度的散度。
直角坐标系下的梯度的掌握情况较好,但是圆柱坐标系和球坐标系下的表达式鲜有学生了解。这主要是由于圆柱坐标系和球坐标系下的梯度表达式相对于直角坐标系更为复杂,学生难以记忆和理解。而在工程实际问题或者习题中,圆柱坐标系和球坐标系在特定情况下会更便于求解,因此,在教学时可为学生提供各坐标系下温度梯度和梯度的散度的表达式,以方便查阅。
3 换热器热计算中的积分
换热器是冷热流体发生热量交换的场所,冷热流体在换热器内沿流动方向不断的吸收或释放热量,对单股流体来说,其温度是不断发生变化的[3]。因此,在进行热计算时,传热关系式Q=kAΔt中的温差应为对数平均温差Δtm。Δtm的物理意义即为在整个换热面上冷热流体温差的积分平均值[2]。
取换热器中的微元面积dA,dA两侧冷热流体的温度分别为t2和t1,温差,则有下式:
分离变量并在整个换热面上积分得
带入到积分平均式即可得到对数平均温差。
在教学过程中,应像学生强调对数平均温差的物理意义,引导学生了解积分对于实际物理问题的意义,加深学生对对数平均温差的理解。
4 迭代求解方程组
在传热学的数值解法中,求解代数方程组的方法分为直接解法和迭代法;迭代法需要首先對计算区域或各离散节点上的数值进行假定,随后在迭代过程中不断用变量的旧值递推新值,直到计算后的结果与前一轮计算所得到的结果的差值小于允许值[4]。在教学过程中,发现部分学生容易对Jacobi迭代与Gauss-Seidel迭代两种方法产生混淆,需要在授课时对两种基本的迭代方法及优缺点进行说明。Jacobi迭代每轮计算均使用上一轮计算所得到的数值,其计算公式简单,计算过程中原始矩阵保持不变,容易并行计算,但是收敛速度慢,占据的数据空间较大。Gauss-Seidel迭代在计算过程中,总是使用最新值,因此需要的存储空间较小,收敛速度较快[5]。
此外,在换热的校核计算过程中,若已知冷热流体进出口温度的其中两个,通常需要对未知的某个温度进行假设进行试算。试算的基本思路与迭代是相似,通过假定一个初值,完成整个计算过程,通过对比计算前后的参数值,判断是否计算结束。
在课堂教学过程中,应结合例题,使学生深入理解迭代法的思路与求解过程,以免造成学生无法完成传热学计算。
5 结语
作为能源动力类学科的专业基础课程,传热学的学习程度直接影响学生后续专业课的学习。在强调课程重要性的同时,如何提高课堂教学效果,加强学生理解能力,也是传热学课程教学过程中需要关注的重点。在传热学课程中强调数学基础知识,一方面可以兼顾数学基础薄弱学生的课堂体验,另一方面,也可以使学生在传热学课程的学习过程中进一步理解数学知识,使数学素质得到进一步提高,提高学生解决实际问题的能力。
【参考文献】
[1]同济大学数学系.高等数学(第七版)[M].高等教育出版社,2014.
[2]杨世铭,陶文铨.传热学.第4版[M].高等教育出版社,2006.
[3]史玉凤,郭彦,何光艳.基础数学知识在传热学教学中的应用[J].中国电力教育,2014(12):88-89.
[4]邓建中,刘之行.计算方法-第2版[M].西安交通大学出版社,2001.
[5]陶文铨.数值传热学(第2版)[M].西安交通大学出版社,2001.
