无轴传动凹版印刷机的相邻偏差耦合同步控制

2018-01-04吕延军张永芳赵晶群肖良君

振动、测试与诊断 2017年6期

刘成，吕延军，张永芳，赵晶群，肖良君

(1.西安理工大学陕西省机械制造装备重点实验室西安，710048) (2.重庆大学机械传动国家重点实验室重庆，400044)(3.西安理工大学印刷包装与数字媒体学院西安，710048)

刘成1,2，吕延军1,2，张永芳2,3，赵晶群3，肖良君3

针对无轴传动凹版印刷机的同步协调控制，考虑印刷基体张力恒定和套印准确的要求，基于相邻偏差耦合思想提出了一种能同时满足凹版印刷机无轴传动系统完全同步和比例同步特点的控制结构。针对无轴传动系统动力驱动部件非线性、强耦合的特点，设计了2阶自抗扰控制器以实现收放卷牵引单元与印刷色组单元高精度的跟踪控制和扰动补偿。构建了无轴传动凹版印刷机同步控制策略的仿真模型，仿真结果表明，提出的同步控制结构具有较高的同步控制精度和稳定性，设计的自抗扰控制器具有较好的速度跟踪性能和抗扰能力。

凹版印刷机；自抗扰控制；交流永磁同步电机；同步控制；相邻偏差耦合

引言

随着电机控制技术的发展，无轴传动技术以其独立动力驱动和柔性联接的特点被广泛应用于现代机械的动力传递，尤其是精密高效的数控机床、现代印刷包装设备及风电机组等[1-3]。在印刷包装设备领域，无轴传动系统通常配置在机组式凹版印刷机中以驱动印版辊筒，实现印刷基体的传递、图文的复制[4]。对于彩色印刷而言，图文复制质量的关键在于各印刷版辊的套印精度，而无轴传动系统各色组及牵引单元间的同步协调性能是影响套印精度最主要的因素之一。因此，实现凹版印刷机无轴传动系统的高精度同步协调控制受到了广泛的关注。

无轴传动系统中各色组及牵引单元均采用独立电机驱动，且其驱动辊/版辊与电机主轴刚性联接，因此无轴传动凹版印刷机同步协调运行的实质在于各驱动电机速度/位置的同步协调配合。目前，有关多电机系统同步协调控制的研究多基于耦合的同步控制结构，并结合各类控制算法展开。文献[5]基于主从同步控制结构，结合比例积分微分(proportion integration differentiation, 简称PID)算法，提出了多轴医疗机器人系统的同步控制方案。文献[6-7]对典型的主从同步控制结构进行了改进，提高了同步控制精度和从轴的抗扰能力。在主从同步控制结构中，由于从轴的扰动信息不能与主轴或其他从轴共享，使得系统的同步性能易受从轴扰动的影响。为了实现系统各轴信息共享，文献[8-9]给出了一种电子虚拟总轴同步控制策略，即将各轴电机的转矩进行综合运算，并反馈到一虚拟总轴上形成控制指令以驱动电机，实现同步。但是这种控制策略的计算机实现较为复杂，其转矩信息的获取尚待进一步研究[7]。

交叉耦合控制策略通过在各电机的反馈信号中引入耦合联接，能够实现各轴信息的共享，且其工程实现较为容易，因此目前较多的研究围绕交叉耦合同步控制策略及其改进形式展开以进一步提高系统的同步协调能力。文献[10-14]通过在各轴之间引入交叉耦合参数或设计交叉耦合控制器，给出了一种针对双电机系统的交叉耦合同步控制策略。但是对于数量大于2的多电机系统，交叉耦合同步控制策略会变得格外复杂而不再适用[15]。为了将交叉耦合同步控制策略扩展到数量大于2的多电机系统，文献[16]针对多感应电机系统在加速和负载变化时的同步协调控制，考虑相邻两电机的状态，给出了一种相邻交叉耦合同步控制策略。文献[17]通过考虑每台电机的跟踪误差及其与相邻电机的同步误差，提出了一种环形耦合同步控制策略。文献[18]考虑电机输出转速与平均输出转速的偏差，提出了一种平均偏差耦合同步控制策略。上述控制策略均能够实现多电机系统的完全同步控制，且具有较好的同步性能。但是对于无轴传动凹版印刷机而言，其收放卷牵引单元与印刷色组单元的角速度比例同步，印刷色组单元间的角速度完全同步，上述同步控制策略尚无法实现。

为此，笔者考虑印刷基体张力恒定和套印准确的要求，基于相邻偏差耦合思想提出了一种机组式无轴传动凹版印刷机的角速度同步控制结构。同时，设计了2阶自抗扰控制器(auto-disturbance rejection controller, 简称ADRC)以提高收放卷牵引单元和印刷色组单元的角速度跟踪能力和抗扰性能。同步控制策略的仿真实验表明了该策略的有效性。

1 单轴伺服系统模型

机组式凹版印刷机由收放卷牵引单元、印刷色组和收放卷单元组成，如图1所示。印刷过程中，收放卷牵引单元驱动辊和印刷色组版辊在电机的驱动下保持同步协调运行，以实现进出印刷色组单元的基体张力恒定和套印准确。由于交流永磁同步电机(permanent magnet synchronous motor, 简称PMSM)结构简单、运行可靠，因此广泛用于凹版印刷机各单元的动力输入。

图1 机组式无轴传动凹版印刷机Fig.1 Unit type shaftless driven gravure printing machine

PMSM是一个转子磁链与电压强耦合的非线性系统[19]。为了便于控制分析，采用矢量控制技术，将电压、电流转变到正交旋转dq坐标中以实现磁链和电压的解耦。假设电机各相绕组对称分布，且不考虑电机的铁心饱和与磁滞损耗，则PMSM在旋转坐标系的数学模型[13]可表示为

(1)

其中：Lsd，Lsq分别为定子绕组d，q轴的电感；Rs为定子绕组电阻；ψr为转子磁链；np为极对数；B为黏滞摩擦因数；J为转子转动惯量；id，iq分别为定子电流在d，q轴上的分量；ud，uq分别为定子电压在d，q轴上的分量；ω为转子转速；Tl为负载转矩；Te为电磁转矩。

采用id=0的矢量控制方法对PMSM进行控制，使得电磁转矩Te与定子电流iq线性正相关，从而获得与直流电机相同的调速性能。对于PMSM的电流环，采用比例积分(proportion integration,简称PI)算法以实现d，q轴电流的闭环控制。另外，为了提高母线电压利用率，便于数字化实现，运用空间电压矢量方法(space vector pulse width modulation, 简称SVPWM)进行脉宽调制。

2 同步控制结构的设计

根据凹版印刷的工作特点和胡克定理，收放卷牵引单元驱动辊与印刷色组版辊的线速度应保持相等以实现印刷基体进出印刷色组单元时的张力恒定。由于凹版印刷机的套准和张力控制一般通过调节PMSM的角速度实现，因此，为了便于实现同步控制与套准、张力控制的一体化，从凹版印刷机收放卷牵引单元与印刷色组单元的角速度关系出发，进行无轴传动系统的同步协调控制。凹版印刷机收放卷牵引单元与印刷色组的角速度关系为

(2)

其中：ωs，ωq分别为收放卷牵引单元驱动辊的角速度；ωi(i=1，2，…，n)为印刷色组单元版辊的角速度；Rs，Rq分别为收放卷牵引单元驱动辊的半径；R分别为印刷色组单元版辊的半径；λs=R/Rs，λq=R/Rq为收放卷牵引单元的传动比。

在凹版印刷机运转过程中，印刷色组单元间的角速度相等，印刷色组单元与收放卷牵引单元的角速度呈现出一定的比例。针对凹版印刷机无轴传动系统的这一特点，考虑张力波动和套准误差对收放卷牵引单元与印刷色组单元角速度输入的影响，定义收放卷牵引单元与印刷色组单元的跟踪误差分别为

(3)

其中：ω*(t)为印刷基准角速度输入；ωq*(t)，ωs*(t)分别为张力波动对放卷和收卷牵引单元造成的角速度输入；ωi*(t)为套准误差对印刷色组单元i造成的角速度输入。

为了确保印刷机组各版辊间的角速度完全同步及其与收放卷牵引单元驱动辊的角速度比例同步，在保证跟踪误差趋于零的同时，应使得

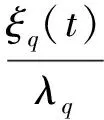
(4)

为此，分别定义放卷、收卷牵引单元、印刷色组单元与其相邻两单元间的同步误差分别为

(5)

(6)

(7)

其中：εs1(t)，εq1(t)，εi1(t)分别为收放卷牵引单元、印刷色组单元i与前一单元的角速度同步误差；εs2(t)，εq2(t)，εi2(t)分别为收放卷牵引单元、印刷色组单元i与后一单元的角速度同步误差。

当所有的同步误差趋于零时，式(4)可以实现。

根据相邻偏差耦合思想，在对一个单元进行控制时，仅仅需要考虑与之相邻两个单元输出信号的偏差情况，且须使得当前单元的跟踪误差及其与相邻两单元的同步误差稳定地收敛于零。为此，定义包含放卷、收卷牵引单元与印刷色组单元同步误差和跟踪误差的耦合误差量分别为

(8)

其中：βq，βi，βs分别为跟踪误差与同步误差之间的耦合系数；Jq，Js分别为放卷和收卷牵引单元驱动辊的转动惯量；Ji为印刷色组单元i的版辊转动惯量。

3 2阶自抗扰控制器的设计

为了消除耦合误差量，实现角速度的准确跟踪与协调同步，针对无轴传动系统非线性、强耦合的特点，设计了2阶ADRC，如图2所示。从图2中可以看出，ADRC主要由微分跟踪器(tracking-differentiator, 简称TD)、扩张状态观测器(extended state observer, 简称ESO)、非线性误差反馈控制律(nonlinear states error feedback control law, 简称NLSEF)构成。

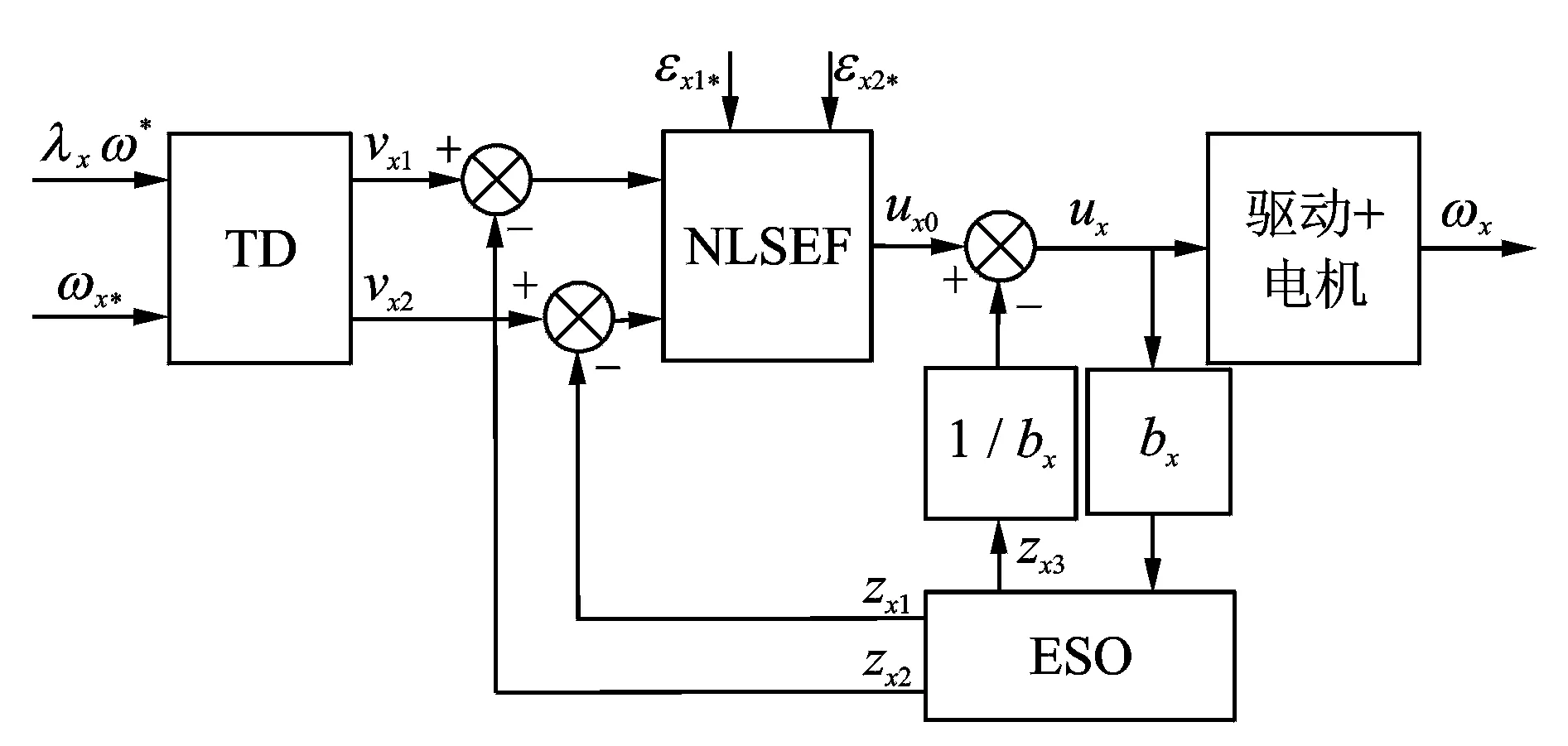
图2 2阶自抗扰控制器结构Fig.2 Second order active disturbance rejection controller structure

考虑到套准误差或张力波动较大时角速度输入造成的系统超调，利用TD安排角速度输入信号的过渡过程，并提取其微分信号。其算法表达式为

(9)

其中：下标x分别代表收放卷牵引单元和印刷色组单元；hx=0.01为采样步长；h0x=0.01为滤波因子；r0x=25为速度因子；fhan为最速控制函数。

fhan表达式为

fhan(x1,x2,r0,h0)=-sign(a)r0[1-

(10)

其中

(11)

利用3阶ESO获得收放卷牵引单元、印刷色组单元角速度输出的跟踪信号zx1及其微分信号zx2，并对内、外部干扰zx3进行估计和补偿[20]。3阶ESO的算法表达式为

(12)

其中：erx(t)为角速度观测误差；fe1x，fe2x为输出误差校正率；bx为补偿因子；γ01x=100，γ02x=300，γ03x=1 000为输出误差校正增益； fal为饱和函数[4]，其非线性因子和线性区间长度的取值分别为0.25和0.5。

为了消除耦合误差，采用fhan函数设计NLSEF以对跟踪误差、同步误差及其导数进行非线性配置。NLSEF的算法表达式为

(13)

其中：r1x=5为控制量增益；h1x，cx分别为精度因子和阻尼系数；εx1*(t)，εx2*(t)分别为εx(t)的跟踪信号及其微分信号；ux0(t)，ux(t)分别为扰动补偿前后的控制信号。

4 仿真与分析

针对具有2个印刷色组单元的无轴传动凹版印刷机进行同步控制策略的仿真分析。取PMSM的参数为：Rs=2.875 Ω，Lsd=Lsq=8.5 mH，Ψr=0.175 Wb，J=0.8×10-3kg·m2，B=0，np=4；PMSM电流环PI控制器的比例与积分系数分别取为21.2和0.5；耦合系数βq=1.75，βi=1，βs=1.75；收、放卷牵引单元的传动比λs=0.6，λq=0.8。收、放卷牵引单元与印刷色组单元的ADRC参数如表1所示。

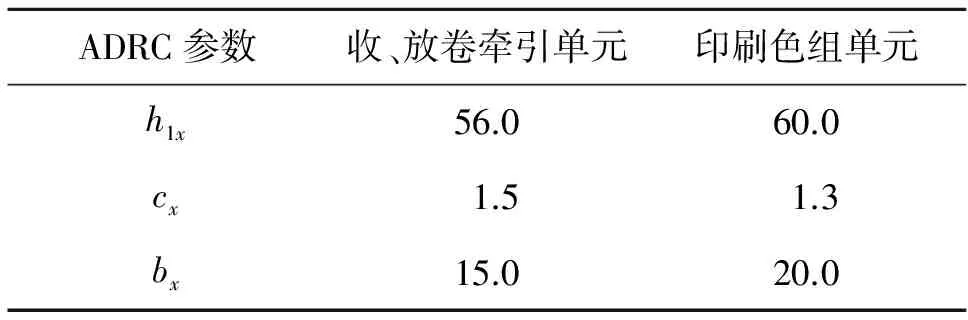
表1 ADRC参数取值

采用设计的同步控制结构，当印刷基准角速度ω*(t)从200 rad/s跳变到400 rad/s时，图3和图4给出了ADRC和PI控制下收、放卷牵引单元和印刷色组单元的角速度响应曲线。从图3和图4可以看出，采用ADRC和PI控制时，各单元均能够迅速响应，并稳定收敛。PI控制时，放卷牵引单元、印刷色组单元1，2与收卷牵引单元分别产生了约6.25%，8.75%，7.75%和8.13%的超调。ADRC控制时，仅放卷牵引单元产生了约1.31%的超调量。

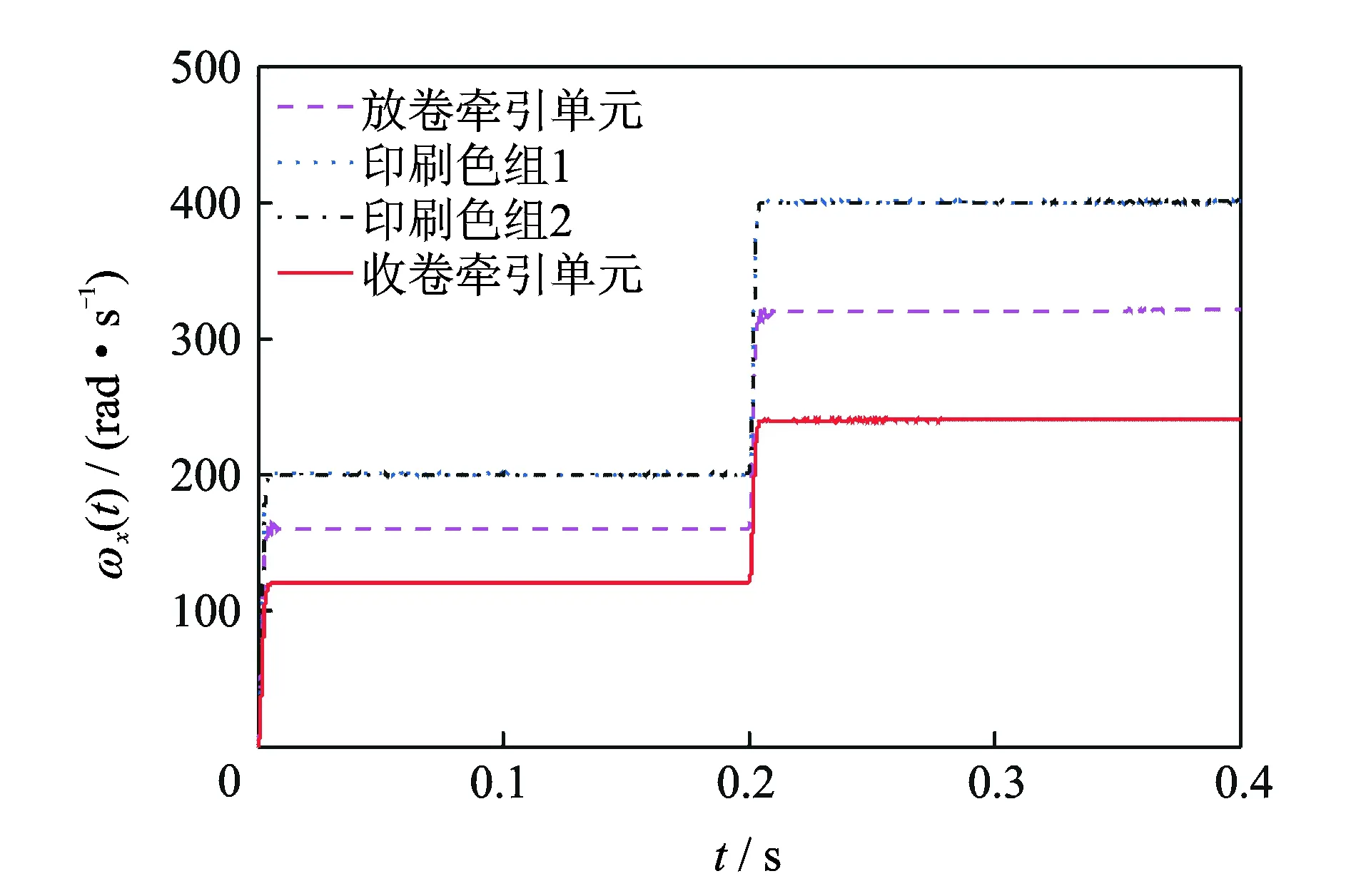
图3 ADRC控制时收、放卷牵引单元和印刷色组单元的角速度响应Fig.3 Angular velocity responses of winding traction unit, unwinding traction unit and printing units with ADRC controller

图4 PI控制时收、放卷牵引单元和印刷色组单元的角速度响应Fig.4 Angular velocity responses of winding traction unit, unwinding traction unit and printing units with PI controller

为了分析张力波动或套准误差发生后的同步控制性能，给定印刷基准角速度ω*(t)为200 rad/s，假设t=0.2 s时印刷色组2存在张力波动或套准误差，其等效瞬时角速度输入为ω2*(t)=20 rad/s。图5给出了印刷色组2的角速度响应曲线，从图5可以看出，与并行同步控制结构相比，采用笔者设计的同步控制结构时，印刷色组2的稳定时间减少了50.0%，超调量减少了11.2%。图6和图7分别给出了印刷色组2与印刷色组1、收卷牵引单元之间的同步误差曲线。从图6和图7可以看出，与并行同步控制结构相比，采用笔者设计的同步控制结构时，同步误差能够在更短的时间内收敛，且超调量下降了约18.6%。

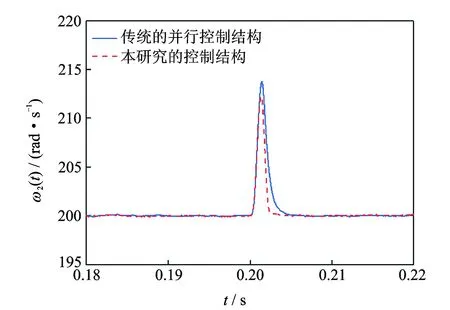
图5 张力波动和套准误差发生时印刷色组2在不同控制结构下的角速度响应Fig.5 Angular velocity responses of printing unit 2 for different control structures when tension fluctuation and register error arises

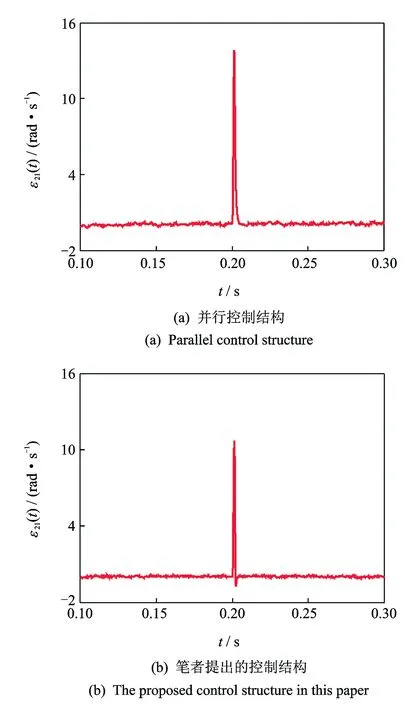
图6 张力波动和套准误差发生时印刷色组1，2在不同控制结构下的同步误差曲线Fig.6 Synchronized errors between printing units 1 and 2 for different control structures when tension fluctuation and register error arises

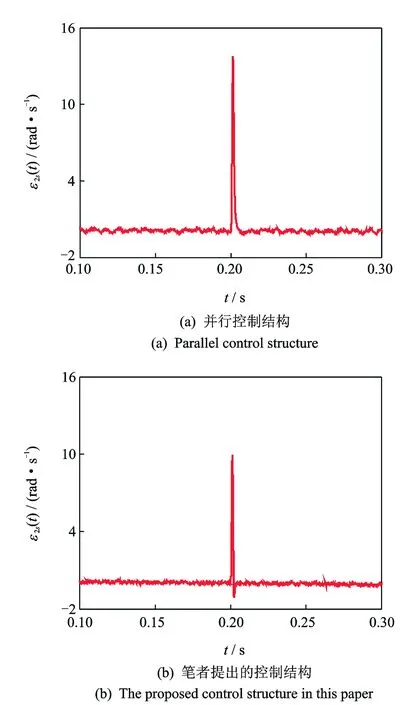
图7 张力波动和套准误差发生时印刷色组2与收卷牵引单元在不同控制结构下的同步误差曲线Fig.7 Synchronized errors between printing unit 2 and winding traction unit for different control structures when tension fluctuation and register error arises

为了分析负载扰动对同步控制结构性能的影响，假设印刷色组单元2在t=0.2 s时发生大小为4 N·m的负载扰动，图8给出了其角速度响应曲线。从图8可以看出，较并行同步控制结构而言，笔者设计的同步控制结构具有较小的速度跟踪误差和稳定时间。图9和图10分别给出了印刷色组2与印刷色组1、收卷牵引单元之间的同步误差曲线。从图9和图10可以看出，较并行同步控制结构而言，采用笔者设计的同步控制结构时，最大同步误差下降了76.6%，约为1.8 rad/s，稳定时间缩短了85.7%，约为0.001 s。

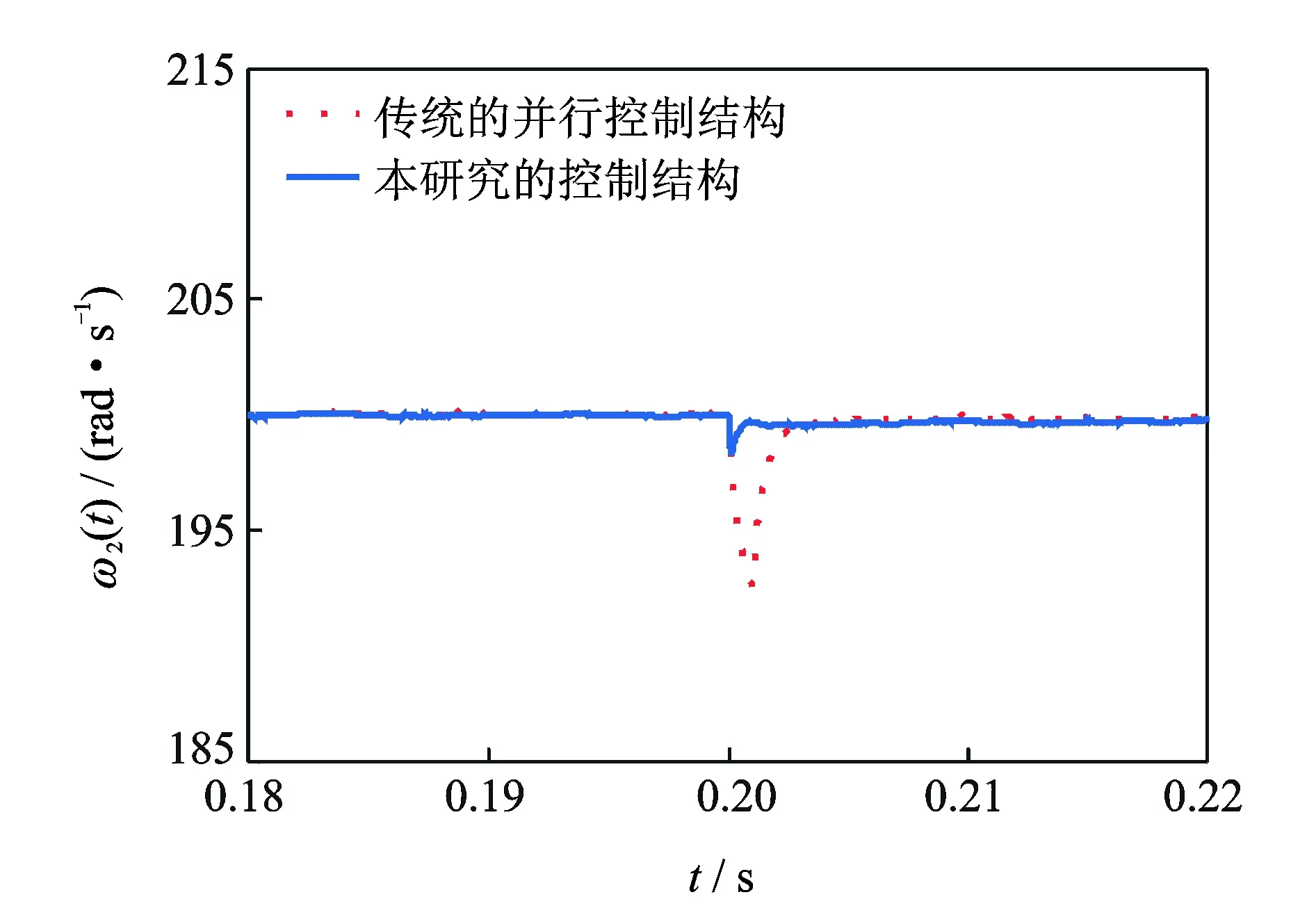
图8 负载扰动时印刷色组2在不同控制结构下的角速度响应Fig.8 Angular velocity responses of printing unit 2 for different control structures with load disturbance

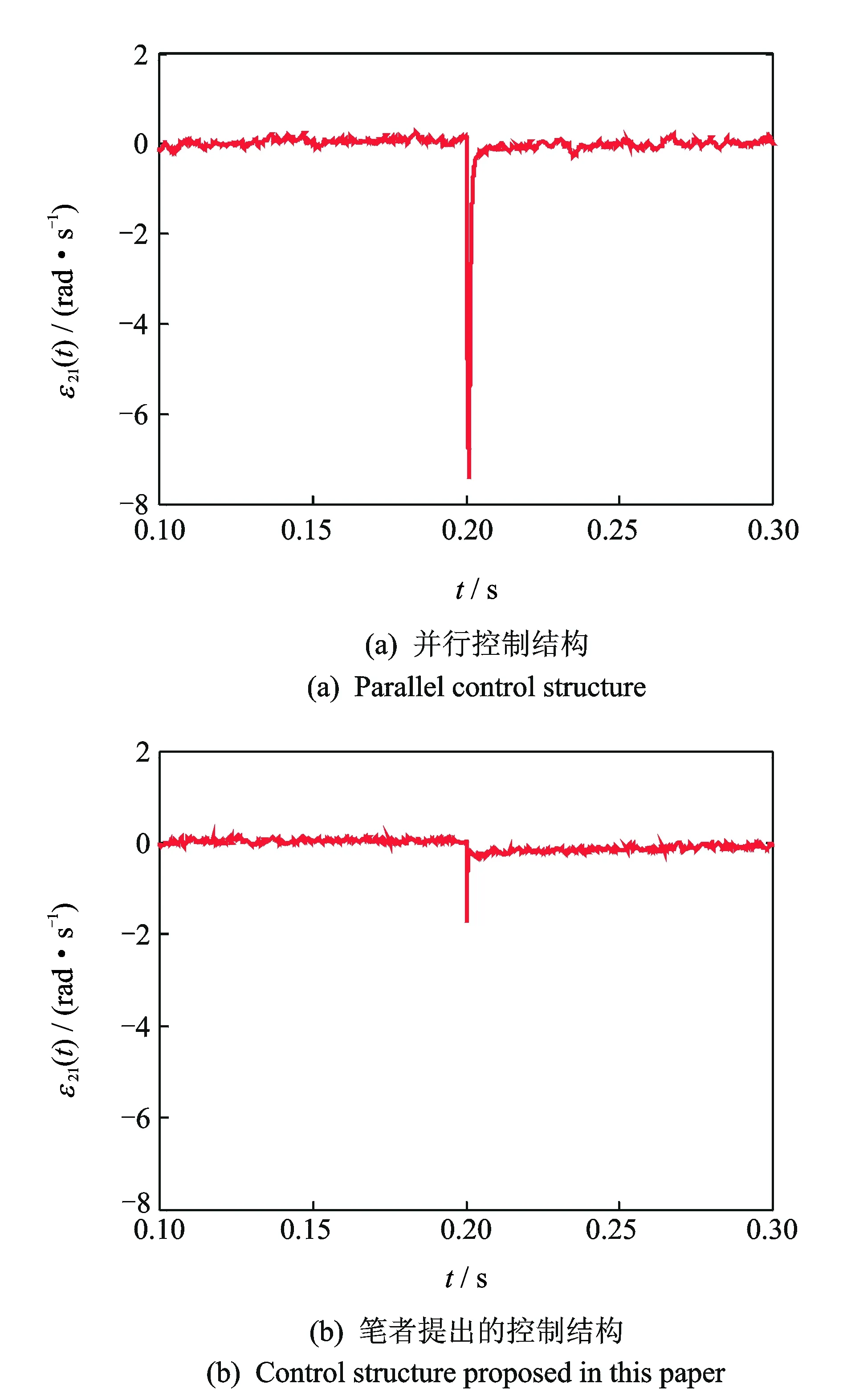
图9 负载扰动时印刷色组1，2在不同控制结构下的同步误差Fig.9 Synchronized errors between printing units 1 and 2 for different control structures with load disturbance

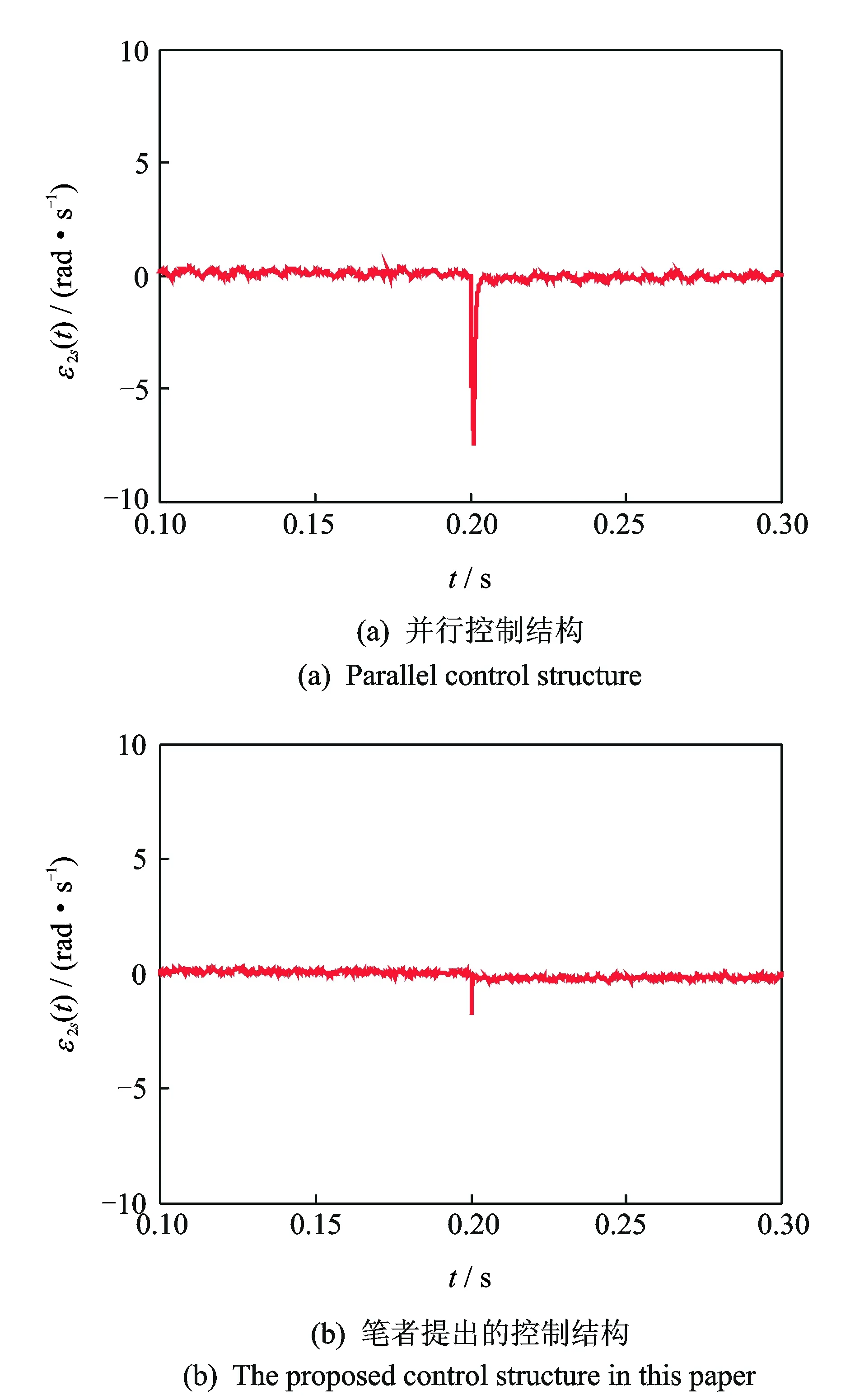
图10 负载扰动时，印刷色组2与收卷牵引单元在不同控制结构下的同步误差Fig.10 Synchronized errors between printing unit 2 and winding traction unit for different control structures with load disturbance

5 结论

1) 考虑印刷基体张力恒定和套印准确的要求，提出了一种基于相邻偏差耦合思想的同步控制结构，同时实现了收、放卷牵引单元与印刷色组单元之间的比例同步控制以及印刷色组单元之间的完全同步控制。与并行同步控制结构相比，提出的同步控制结构具有更高的同步精度。

2) 针对收、放卷牵引单元及印刷色组动力驱动部件非线性、强耦合的特点，设计了2阶ADRC控制器，实现了收放卷牵引单元与印刷色组的跟踪控制和扰动补偿。与PI控制器相比，ADRC控制器能够快速稳定地消除角速度跟踪误差，具有更好的抗扰能力。

[1] Conway J R，Ernesto C A，Farouki R T，et al. Performance analysis of cross-coupled controllers for CNC machines based upon precise real-time contour error measurement[J]. International Journal of Machine Tools and Manufacture，2012，52(1)：30-39.

[2] Kang D，Lee E，Kim H, et al. Investigation on synchronization of the offset printing process for fine patterning and precision overlay[J].Journal of Applied Physics，2014，115(23)：234908.

[3] Cardenas R，Pena R，Alepuz S，et al. Overview of control systems for the operation of DFIGs in wind energy applications[J]. IEEE Transactions on Industrial Electronics，2013，60(7)：2776-2798.

[4] 刘善慧，梅雪松，李健，等. 多色套准系统前馈自抗扰控制器的设计[J]. 机械工程学报，2015，51(5)：143-152.

Liu Shanhui，Mei Xuesong，Li Jian，et al. Design feed forward active disturbance rejection control controller for multi-color register system[J]. Journal of Mechanical Engineering，2015，51(5)：143-152. (in Chinese)

[5] Salimi A，Ramezanifar A，Grigoriadis K M. Control of a cable-driven platform in a master-slave robotic system：linear parameter varying approach[J]. Journal of Dynamic Systems，Measurement，and Control，2015，137(9): 094502.

[6] Su Housheng，Chen M Z Q，Wang Xiaofang，et al. Semiglobal observer-based leader-following consensus with input saturation[J]. IEEE Transactions on Industrial Electronics，2014，61(6): 2842-2850.

[7] Zhang Changfan，Wu Han，He Jing，et al. Consensus tracking for multi-motor system via observer based variable structure approach[J]. Journal of the Franklin Institute-Engineering and Applied Mathmatics，2015，352(8): 3366-3377.

[8] Wolf C M，Lorenz R D，Valenzuela M A. Digital implementation issues of electronic line shafting[J]. IEEE Transactions on Industry Applications，2010，46(2)：750-760.

[9] Zhang Changfang，He Jing，Jia Lin，et al. Virtual line-shafting control for permanent magnet synchronous motor systems using sliding-mode observer[J]. IET Control Theory and Applications，2015，9(3)：456-464.

[10] Chen C S，Chen L Y. Robust cross-coupling synchronous control by shaping position commands in multiaxes system[J]. IEEE Transactions on Industrial Electronics，2012，59(12)：4761-4773.

[11] Cheng M H，Li Yuejuan，Bakhoum E G. Controller synthesis of tracking and synchronization for multiaxis motion system[J]. IEEE Transactions on Control Systems Technology，2014，22(1)：378-386.

[12] Lin F J，Chou P H，Chen C S， et al. DSP-based cross-coupled synchronous control for dual linear motors via intelligent complementary sliding mode control[J]. IEEE Transaction on Industrial Electronics，2012，59 (2)：1061-1073.

[13] Deng Zhenhua，Shang Jing，Nian Xiaohong. Synchronization controller design of two coupling permanent magnet synchronous motors system with nonlinear constraints[J]. ISA Transactions，2015，59：243-255.

[14] Wu Jianhua，Liu Chao，Xiong Zhenhua，et al. Precise contour following for biaxial systems via an A-type iterative learning cross-coupled control algorithm[J]. International Journal of Machine Tools and Manufacture，2015，93：10-18.

[15] Jian Li，Fang Youtong，Huang Xiaoyan，et al. Comparison of synchronization control techniques for traction motors of high-speed trains[C]∥Electrical Machines and System (ICEMS), 2014 IEEE International Conference. Hangzhou, China: IEEE, 2014：2114-2119.

[16] Zhao Dezong，Li Chunwen，Ren Jun. Speed synchronization of multiple induction motors with adjacent cross coupling control[J]. IET Control Theory and Applications，2010，4(1)：119-128.

[17] Li Lebao，Sun Lingling，Zhang Shengzhou，et al. Speed tracking and synchronization of multiple motors using ring coupling control and adaptive sliding mode control[J]. ISA Transactions，2015，58：635-649.

[18] Li Lebao，Sun Lingling，Zhang Shengzhou. Mean deviation coupling synchronous control for multiple motors via second-order adaptive sliding mode control[J]. ISA Transactions，2016,62:222-235.

[19] 马琮淦，左曙光，何吕昌，等. 电动车用永磁同步电机电磁转矩的解析计算[J]. 振动、测试与诊断，2012，32(5)：756-761.

Ma Conggan，Zuo Shuguang，He Lüchang，et al. Analytical calculation of electromagnetic torque in permanent magnet synchronous motor for electric vehicles[J]. Journal of Vibration, Measurement & Diagnosis，2012，32(5)：756-761. (in Chinese)

[20] 李生权，季宏丽，裘进浩，等. 基于加速度反馈和自抗扰的加筋壁板结构复合振动控制[J]. 振动工程学报，2012，25(5)：530-538.

Li Shengquan，Ji Hongli，Qiu Jinhao，et al. Composite vibration control for a stiffened panel structure using acceleration feedback and active disturbance rejection[J]. Journal of Vibration Engineering，2012，25(5)：530-538. (in Chinese)

10.16450/j.cnki.issn.1004-6801.2017.06.026

陕西省自然科学基金资助项目(2014JN2-5082)；国家自然科学基金资助项目(51505375)；机械传动国家重点实验室开放课题资助项目(SKLMT-KFKT-201510)；陕西省教育厅科学研究计划资助项目(15JS068)

2016-03-13；

2016-04-15

TS835; TH39