基于卷积神经网络的异步电机故障诊断

2018-01-04王丽华谢阳阳周子贤张永宏赵晓平

振动、测试与诊断 2017年6期

关键词：故障诊断卷积神经网络

王丽华，谢阳阳，周子贤，张永宏，赵晓平

(1.南京信息工程大学信息与控制学院南京，210044) (2.南京信息工程大学计算机与软件学院南京，210044)

基于卷积神经网络的异步电机故障诊断

王丽华1，谢阳阳1，周子贤2，张永宏1，赵晓平2

(1.南京信息工程大学信息与控制学院南京，210044) (2.南京信息工程大学计算机与软件学院南京，210044)

由于电机内部结构的复杂性，使得其故障特征与故障类型之间存在较强的非线性关系；目前用于异步电机故障诊断的方法都是人工手动提取特征，这需要大量的先验知识、丰富的信号处理理论和实际经验作为支撑，诊断效率不高；同时用于模式识别时的样本量过少，会导致网络过拟合等问题。针对以上问题，提出了基于短时傅里叶变换(short-time fourier transform，简称STFT)和卷积神经网络(convolutional neural networks, 简称CNN)的电机故障诊断方法。该方法以单一振动信号为监测信号，使用STFT将故障信号转换成时频谱图，构建大量不同故障样本，以确保样本多样性，提高网络鲁棒性。将预处理后的样本作为CNN的输入，有监督地调整网络参数，以实现准确的电机故障诊断。将所提出的STFT+CNN算法分别与传统的电机故障诊断方法及堆叠降噪自编码进行比较分析。试验结果表明，该方法能够更有效地进行电机故障诊断。

电机；振动信号；短时傅里叶变换；卷积神经网络

引言

异步电机在当代社会生产系统中的应用越来越广泛，是工业生产活动的主要驱动设备，一旦发生故障，将带来巨大的经济损失。因此，针对异步电机故障诊断技术的研究，具有重要的理论研究价值和实际意义[1]。异步电机是由定子、转子、轴承、机座和风扇等组成的综合电气设备，其内部包含多个复杂的子系统，使电机故障呈现出多样性，其表现出的特征也千差万别，并且同一症状有可能是不同的原因造成的，同一种故障表现出的特征也不尽相同[2]。因此，异步电机的故障特征与故障类型之间并非一一对应的，其间存在较强的非线性关系[3]。

实际生产中经常产生故障的部位有转子和轴承等。转子故障诊断常用方法是电流分析法。定子电流频谱分析[4](motor current signature analysis, 简称MCSA)是电流分析法中典型的方法，该方法通过分析定子电流频谱判断转子断条故障，但是异步电机正常工作时转差率小，从而使得故障分量和基频分量十分接近，且故障分量幅值很小，易被基频泄露及环境噪声淹没，难以分析判断。Cruz等[5-7]先后提出了Park′s和扩展Park′s矢量方法，两者都是通过分析定子电流频谱进行故障判断。Park′s矢量法将对频谱的分析转化成图形问题，方便了故障识别，但是这种方法却不适用于故障早期；扩展Park′s矢量方法在原有基础上引入了平方项，产生了许多交叉项，使得频谱复杂化。刘振兴等[8]将Hilbert模量定义为原始信号与其共轭信号的平方和，通过Hilbert变换将定子电流信号的基波信号转换成直流分量，从而提取出故障特征分量，但是该方法只采样了单相电流信号，只能完成偏心、断条故障分量提取，而且同样存在交叉项多的问题。方瑞明等[9]将模式识别算法用于解决电机转子故障诊断问题，根据MCSA分析法，分别提取电流基波和谐波信号特征用于支持向量机(support vector machine, 简称SVM)的训练，该方法只完成了电机内部单一转子故障分类，且用于SVM分类器训练的样本量过少。

轴承故障诊断常用方法是振动分析法。由于异步电机内部结构复杂，采集得到的振动信号往往是多个分量的混合，且振动信号具有非平稳、非线性等特点，这使得特征提取变得困难。杨江天等[10]利用经验模态分解(empirical mode decomposition，简称EMD)将电机轴承振动信号分解滤波后进行改进双谱变化，提取故障特征频率。钱华明等[11]利用小波包进行振动信号分解，将各频带能量与总能量的比作为特征送入到改进的遗传小波神经网络中训练，构建诊断网络完成电机故障诊断。上述方法存在两个方面不足：a.以单一的诊断信号完成了异步电机内部某一结构的故障诊断，而异步电机内部结构复杂多样，单一对象的故障诊断无法满足实际需求；b.均采用手动提取特征的方式，需要丰富的先验知识、信号处理理论和实际经验作为支撑，还需要大量人工处理数据的时间。针对前一点不足，李学军等[12]提出将电流信号和振动信号相结合，先用小波包分别提取两类信号的熵特征后，采用具有较强非线性处理能力的核主成分分析(kernel principal component analysis, 简称KPCA)进行特征融合后利用SVM完成转子和轴承的故障诊断，通过500组数据验证得出，信号融合后的效果明显比单一信号好。同样，上述方法中用于故障识别网络训练的样本量太少，这会使得样本的多样性无法得到保证，从而降低网络的鲁棒性。在模型很复杂的情况下，样本过少会使得网络专注解释训练数据，从而降低对未知数据的解释能力，形成过拟合。

针对上述样本量小和手工提取特征的问题，笔者以单一的振动信号为监测信号，将CNN引入到电机故障诊断中，通过STFT求电机振动信号的时频谱图，构建大量表示不同故障的带标签样本数据，以确保样本的多样性，提高网络的鲁棒性。预处理后输入卷积神经网络，利用误差反向传播算法经过多次迭代，从而建立信号和电机故障之间相互联系的网络，实现电机故障的精确诊断。

1 卷积神经网络

CNN是近年发展起来并引起广泛重视的一种高效识别方法[13]。CNN可以将原始图像直接输入，避免了前期对图像的复杂预处理。同时，CNN对平移、比例缩放、倾斜或其他变形形式的图像信息具有高度不变性，因而得到更为广泛的应用。

CNN将多个单层卷积神经网络堆叠，前一层的输出作为后一层的输入，并在最后一层的输出特征图后接上全连接层和分类器，从而用于图像、语音等的识别。

1.1 单层卷积神经网络

每个单层卷积神经网络包括卷积和下采样两个阶段，如图1所示，其中下采样阶段不是每层都必须有的。

图1 单层卷积神经网络Fig.1 Single Convolutional Neural Network

1.1.1 卷积层

自然图像有其固有特性：从图像某一子块学习得到一些特征后，将这些特征作为探测器，应用到所有子块中去，获取不同子块的激活值。CNN中的卷积就利用了图像的这种固有特性，每个卷积核检测输入特征图所有位置上的特定特征，实现了同一输入特征图上的权值共享。为了提取输入特征图不同的特征，则使用不同的卷积核进行卷积操作。图1中使用8个3×3大小卷积核对一张10×10大小的输入特征图卷积，得到8张8×8的特征图。卷积操作的一般形式为

x=f(∑x*wij+b)

(1)

其中：*为二维离散卷积运算符；b为偏置；wij为卷积核；x为输入特征图；f(·)为激活函数。

1.1.2 下采样

通过卷积层，特征图片的个数增加，使得特征维数变得很大，容易造成维数灾难。为了解决这一问题，对卷积得到的特征图进行聚合统计，从而更加方便描述高维图像，这种聚合操作就是下采样。下采样操作在降低了输出特征图分辨率的同时，仍较好地保持着高分辨率特征图描述的特征。下采样的一般形式为

x=f(βdown(x)+b)

(2)

其中：β为乘性偏置；down()为下采样函数；b为加性偏置；f(·)为激活函数。

如图1所示，由输入特征图卷积得到8张8×8的特征图，经过下采样操作后变成8张4×4的特征图，从而降低了特征图的维数。

1.2 全连接层

全连接(层)的所有神经元节点，都与上一层输出的特征图中所有的神经元节点互相连接。其输出为

h(x)=f(wx+b)

(3)

其中：x为全连接层的输入；h(x)为全连接层的输出；w为权值；b为加性偏置；f(·)为激活函数。

为了防止分类时出现过拟合的情况，通常在全连接层引入“Dropout”[14]的方法，即在训练时，以一定的概率P，让隐藏层的某个神经元停止工作，从而提高网络的泛化能力，防止过拟合。

1.3 分类器

Softmax[15]是Logistic分类器的一种推广，主要解决多分类问题。假设训练数据中输入样本为x，对应的标签为y，则将样本判定为某个类别j的概率为p(y=j|x)。所以，对于一个K类分类器，输出的将是一个K维的向量(向量的元素和为1)，如式(4)所示

(4)

在训练中，利用梯度下降法，通过多次迭代使得Softmax的代价函数J(θ)达到最小，从而完成网络训练。其代价函数J(θ)为

其中：1{·}为一个指示性函数，即当大括号内的值为真时，该函数结果就为1；否则结果就为0。

在训练卷积神经网络时，最常用的方法是采用反向传播法则以及有监督的训练方式，根据给定的标签与网络输出的结果进行比较，生成误差项。根据反向传播的思想，将误差逐层传递到每个节点，并更新权值(具体的权值更新公式见文献[16])。通过多次迭代使得误差项越来越小，权值也越来越稳定，从而完成网络的训练。

2 卷积神经网络模型及训练步骤

为了有效地实现电机故障诊断，笔者将短时傅里叶变换和卷积神经网络相结合。卷积神经网络模型如图2所示，其中：C1，C2，C4，C5为卷积层；S3，S6为下采样层；FC1，FC2为全连接层；Softmax为分类层。具体网络参数如表1所示。

图2 卷积神经网络Fig.2 Convolutional neural network

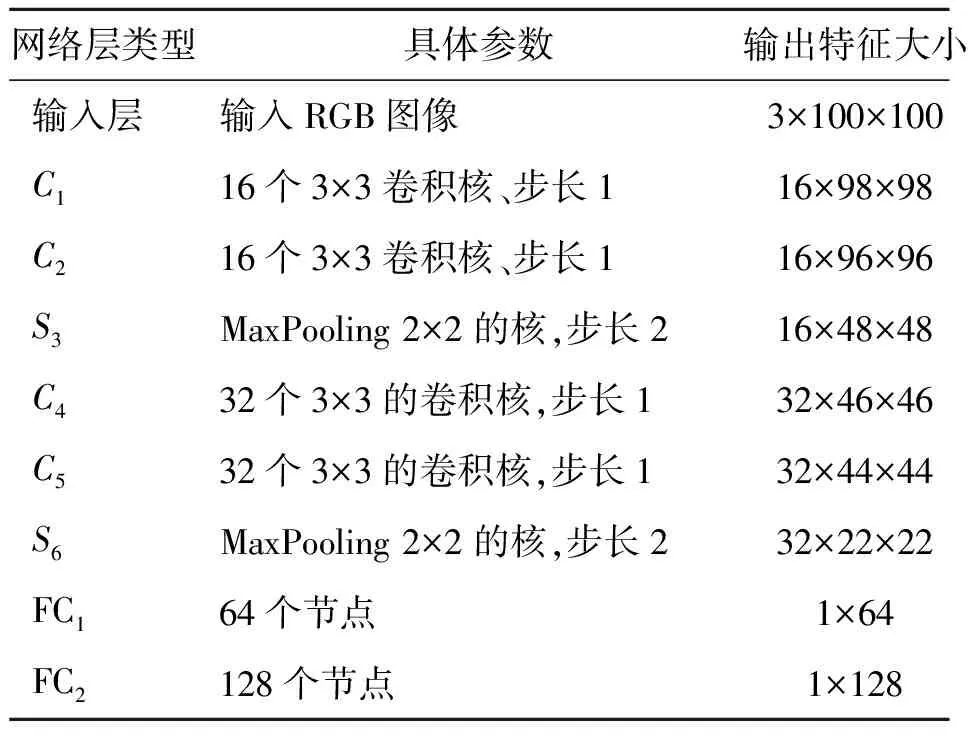
网络层类型具体参数输出特征大小输入层输入RGB图像3×100×100C116个3×3卷积核、步长116×98×98C216个3×3卷积核、步长116×96×96S3MaxPooling2×2的核，步长216×48×48C432个3×3的卷积核，步长132×46×46C532个3×3的卷积核，步长132×44×44S6MaxPooling2×2的核，步长232×22×22FC164个节点1×64FC2128个节点1×128

电机故障诊断过程分为以下9个步骤：

1) 电机振动信号采集；

2) 将振动信号通过短时傅里叶变换转化为时频图；

3) 对时频图进行处理，先将时频图的非特征部分(即空白处和坐标等)删除，再将图片压缩成合适大小的正方形；

4) 建立网络并初始化网络参数，根据样本和要求，构建合适深度的网络模型，确定网络参数(如学习率、迭代次数、步长等)；

5) 网络训练和前向传播，将样本输入到网络中，通过前向传播求得网络输出与预期目标的误差；

6) 判断网络是否收敛，若网络收敛，则执行步骤8，否则执行步骤7；

7) 反向传播和权值修改，利用BP反向传播算法，将步骤5求得的误差反向逐层传播到每个节点，并更新权值，重复执行步骤5～步骤7，直至网络收敛；

8) 根据测试样本的精确度判断网络是否满足实际要求，如满足执行步骤9，否则跳转到步骤4，修改网络参数；

9) 输出网络用于电机故障诊断。

图3为其流程图。

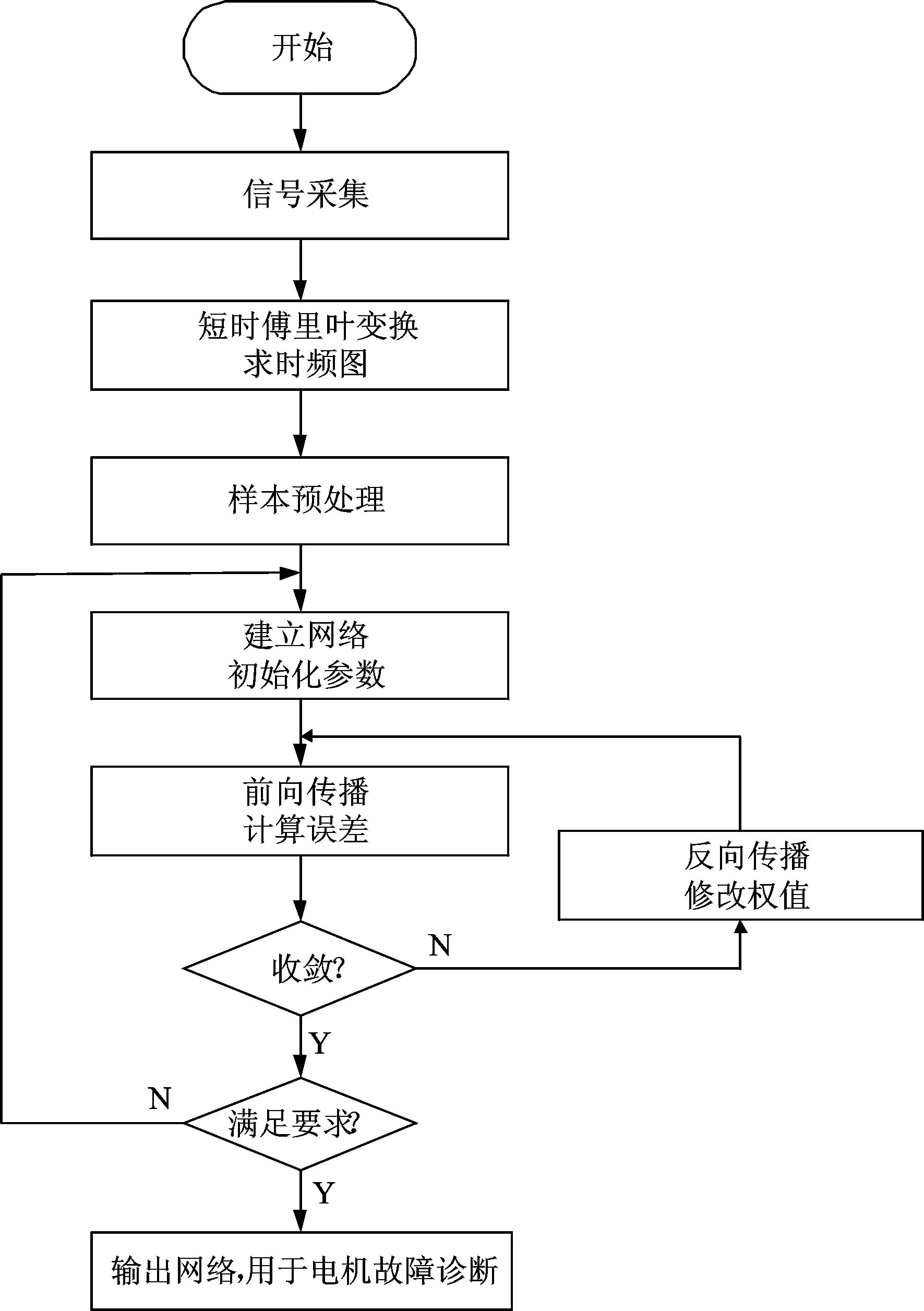
图3 电机故障诊断流程图Fig.3 Flow chart of motor fault diagnosis

3 试验验证

3.1 试验数据

笔者以动力传动故障诊断综合试验台的异步电机为研究对象，将短时傅里叶变换和卷积神经网络相结合，从而完成电机故障的诊断和其状态的监测。该系统由电机、两级行星齿轮箱、定轴齿轮箱和磁粉制动器等组成。本实验将加速度传感器安装在异步电机上，如图4所示。通过更换电机，同时调节不同转速(3 600和3 000r/min),模拟了7种不同的电机健康状态：

1) 无故障；

2) 转子不平衡故障通过在转子两端突出的小铝销上安装配重来实现；

3) 转子弯曲故障的电机包含一个弯曲程度为0.005″～0.01″的故障转子；

4) 轴承故障电机内置一个内圈故障的轴承；

5) 转子断条故障电机同样含有一个故意损坏的转子条；

6) 定子绕组故障的电机在采集数据时，可通过外部控制盒向绕组添加额外的负载，控制箱可变电阻范围为0～4Ω；

7) 电压不平衡单相位故障通过开关相位来实现单相，并用控制箱引入电阻，相位损耗开关将电路切换到第1阶段，电压控制开关向第2相引入0～25Ω的可变电阻，第3相保持不变。

由于试验台模拟故障种类的限制，本研究仅包含了7种故障，但为了增加采样时故障样本的复杂性，采集定子绕组、电压不平衡和单相位故障的数据时，除了改变转速，还对控制箱可变电阻随机调节。

如表2所示，每种故障在相同的工作情况下采集了1 300个时域信号，采样频率为5 120Hz，每个信号时长5s，通过STFT转换成9 100个样本，随机选取不同健康状态的20%样本作为测试样本，其余作为训练样本。

图4 动力传动故障诊断综合试验台Fig.4 Drivetrain dynamics simulator

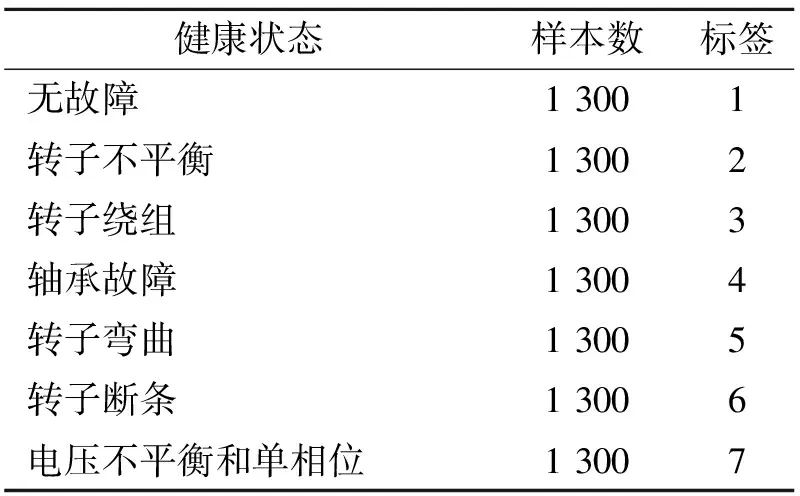
健康状态样本数标签无故障13001转子不平衡13002转子绕组13003轴承故障13004转子弯曲13005转子断条13006电压不平衡和单相位13007

3.2 信号时频图的预处理

使用STFT求得各个故障信号的时频图，并将其简单预处理来提高整个识别系统的实时性和准确性。时频图预处理包括图片的切割和压缩，如图5所示。利用STFT将信号转换成时频谱图，剪切掉时频谱图周边的坐标以及空白部分，为了降低计算量和方便CNN的训练，将图片压缩成100×100的正方形。

图5 时频图的预处理Fig.5 Pre-processing for time frequency diagram

3.3 试验结果分析

将预处理后的时频谱图输入卷积神经网络，多次迭代后其诊断精确度最高为100%(见表3)，充分说明STFT结合CNN的方法能够有效地识别电机故障，完成电机故障的智能诊断。

表3 多次试验结果

试验中，为了更好地了解CNN网络工作的特点，从7种故障中各随机选取一个样本作为输入，对网络C1，C5进行特征可视化，其结果如图6所示。

图6 CNN网络层特征可视化图Fig.6 Feature visualization of CNN network

比较不同故障的特征图能够发现，同一个卷积核对不同故障所提取的特征差异很明显。例如图6(b)中各图的右下角方格，代表C1层最后一个卷积核对不同故障样本提取的特征图，可以发现各图纹理差异很大，这表明卷积核所学到的参数，在特征提取上是有效的。此外，从图6(b)中1可以看出，不同卷积核对同一个故障样本提取特征时，能够自适应地学习出不同的纹理特征，对于部分没有学习到特征的卷积核，可以考虑对网络结构进行裁剪，去除未学习到特征的卷积核。

为了定量显示CNN网络提取特征的能力，笔者选取7种故障各自的样本作为输入，分别提取CNN网络FC2层的特征，计算两两之间的相关性，其结果如图7所示。

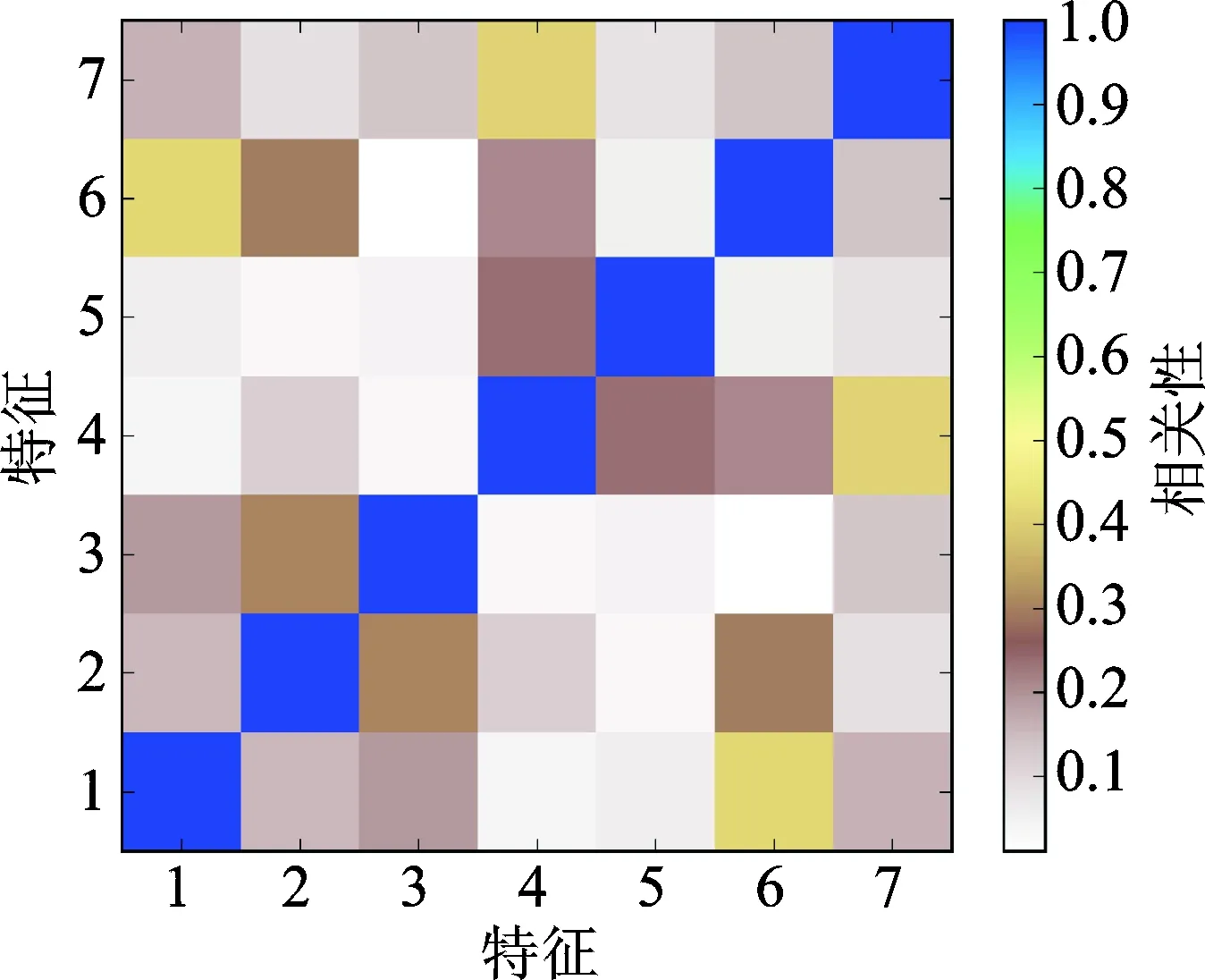
图7 FC2层特征之间的相关性图Fig.7 Correlation diagram between FC2 layer features

图7显示了FC2层特征相关性，若两者之间相关性最高，则该点的数值最大，显示为蓝色；反之，若两者之间的相关性最弱，则该点是数值最小，显示为白色。相关系数反映的为不同故障提取出的特征之间的差异，相关系数越小，表明不同故障提取出的特征差异性越大。从图7中看出，不同故障样本之间的相关系数都小于0.5，即不同故障样本经CNN提取出的FC2层特征具有较强的识别度，说明CNN具有很好的特征提取能力。

3.4 不同参数下卷积神经网络训练情况对比

3.4.1 学习率对卷积神经网络训练的影响

在训练卷积神经网络时，运用了梯度下降法进行优化，其中学习率是影响权值调整、误差收敛的一个重要参数。为了提高网络训练的效率，选择一个合适的学习率十分重要。在本试验中，采用不同学习率训练卷积神经网络，如图8所示(其余参数相同)。

由图8可以看出，学习率太大或者太小，CNN的训练正确率和测试正确率都会降低，同时损失值都会变大。选择合适的学习率，能够加快CNN网络收敛的速度，提高网络的精度。本试验选择的学习率为0.005。

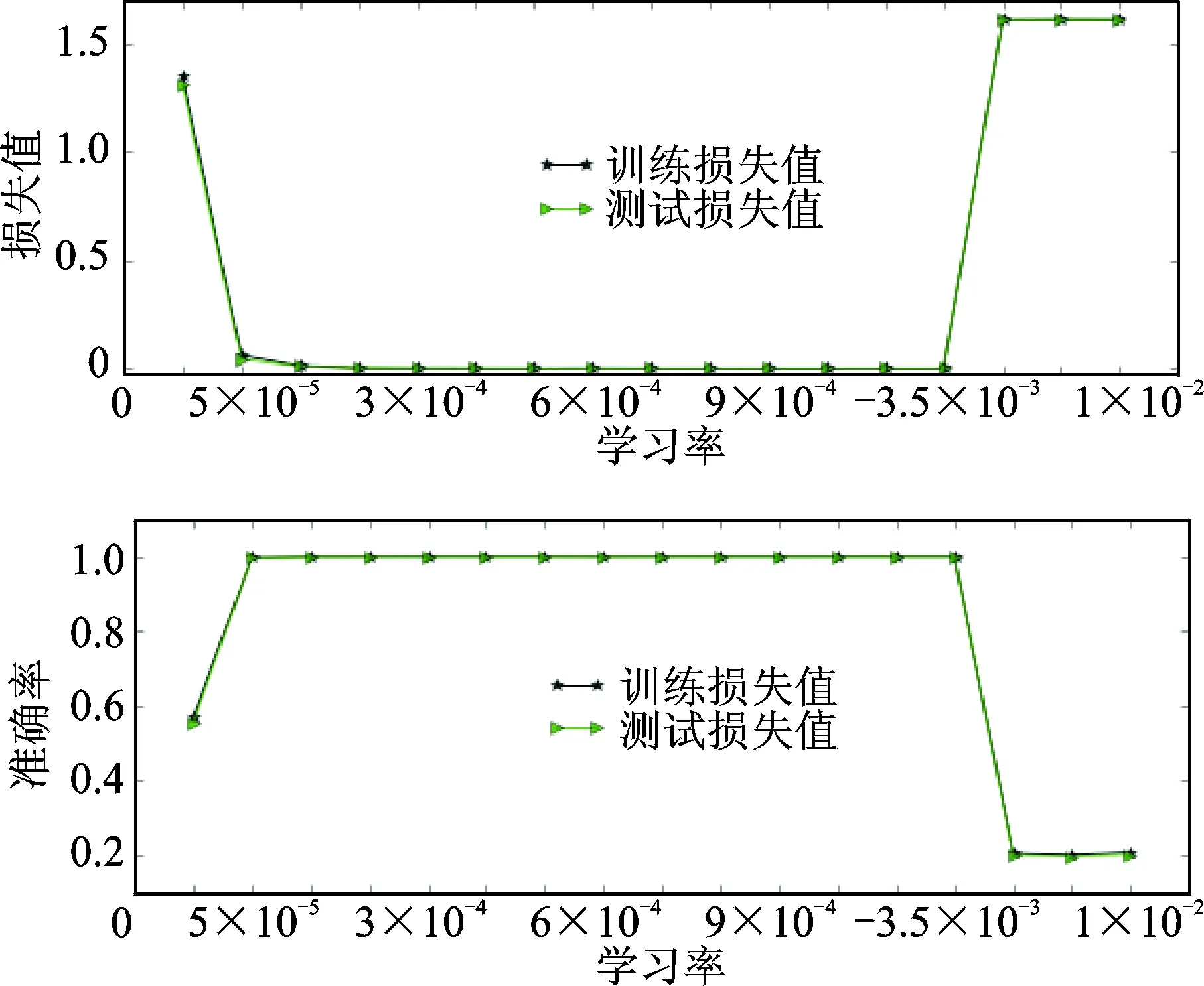
图8 不同学习率对CNN训练的影响Fig.8 Effect of different learning rate on CNN training

3.4.2 Batchsize对卷积神经网络训练的影响

在训练CNN时，由于样本数据量大、电脑配置有限等条件的限制，无法一次将所有样本全部用于网络的训练，因此，通常会选择将样本平均分成大小适中的块，这个块的大小就是Batchsize。本试验使用不同Batchsize，对CNN进行训练(其他参数相同)，其结果如图9所示。图10为不同Batchsize条件下，CNN迭代一次需要的时间。

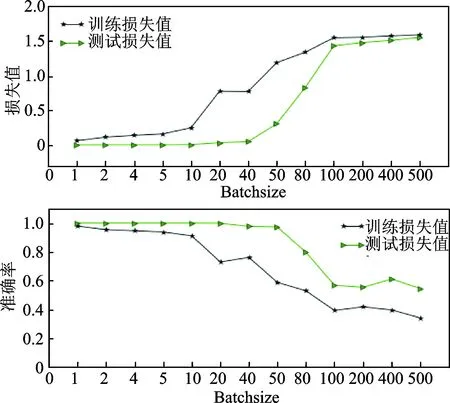
图9 不同Batchsize对CNN训练的影响Fig.9 Effect of different batchsize on CNN training

图10 CNN在不同Batchsize下迭代一次所花时间Fig.10 Time of one iterative with different batchsize

从图9、图10可以看出，当Batchsize很小时，网络训练和测试的精确度都很高，但是迭代一次所需要的时间却很长。当Batchsize越来越大，其训练和测试的精确度越来越低，但迭代一次所需要的时间却变少。本试验采用的Batchsize为20，保证准确度的同时，降低了训练所需要的时间。

训练CNN时选择合适的参数很重要，不同样本集的参数是不同的。调整参数，找到对应样本集合适的参数，是CNN训练过程中的重要的环节。

3.5 与其他方法对比分析结果

为了说明卷积神经网络在电机故障诊断中的优势，笔者对其进行比较分析，各方法均采用3.1节中采集的数据。

3.5.1 与传统电机故障诊断方法比较分析

特征提取和模式识别是电机故障诊断的两个主要过程[17]。目前特征提取的主要方法有EMD[18]和PCA[19]等，也可以通过分析电机信号的均值、方差、峭度、峰值和能量比等完成特征提取。常用于电机故障诊断的方法有BP神经网络和SVM[20]等。

本研究将CNN与PCA+SVM，EMD+SVM、诊断特征+SVM等方法进行比较，其结果如表4所示。试验中，所使用的电机数据来自于采集得到的同一个电机故障信号数据集。从PCA，EMD及诊断特征等方法本身的特点和在信号处理领域的实际应用意义来看，这些方法都以时域信号为基础来提取特征。为了方便CNN的使用，利用STFT将时域信号转化成时频谱图，用于网络训练。虽然诊断方法的样本不一样，样本数也不一样，但是都取之同一个数据集，因此具有一定的对比意义。

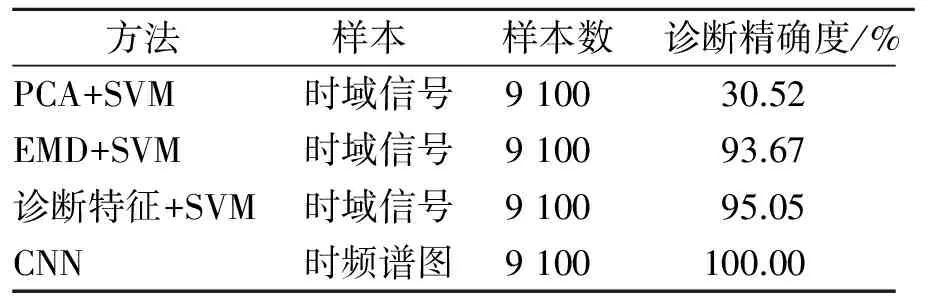
表4 不同电机故障诊断方法的结果

PCA+SVM方法主要利用PCA来提取时域信号特征(特征数从2～100)，结合SVM完成电机故障诊断。但是PCA在本质上是一种线性方法，处理非线性问题能力差，因此PCA+SVM方法效果差，其平均诊断精确度为30.52%。EMD能够自适应地实现信号分解，较小波分析方法有很大的优势，试验以EMD分解出的IMF分量能量值作为特征，训练SVM分类器以完成故障诊断。试验中从时域信号和频域信号分别提取多个诊断特征，这些特征能够很好地描述故障信号所包含的信息，因此EMD+SVM和诊断特征+SVM两种方法能够较好地实现电机故障诊断，其诊断精确度分别为93.67%和95.05%。CNN因多层网络的映射和有监督的参数调整，能够准确实现电机故障诊断，其诊断精确度为100%。本试验所用方法基于KERAS框架实现，虽然在迭代50次的情况下所花训练时间为0.6h，但在用于测试100个样本时所花时间仅为2s，具有极高的实时性。

3.5.2 与其他深度学习模型(堆叠降噪自编码)的比较

堆叠降噪自编码(stacked denoising auto-encoder,简称SDAE)是由自编码堆叠而成的无监督深层网络，可以通过有监督的全局微调实现故障诊断。本研究将CNN与SDAE在电机故障诊断方面进行比较，如表5所示。CNN网络的样本是时频谱图，时频谱图是由时域信号(在4.1节说明了时域信号长度为5s)转换而来，而SDAE网络的样本为时域信号(时域信号长度为2 000个点，即为0.4s，由于电脑配置等条件限制，其样本不宜过大)。

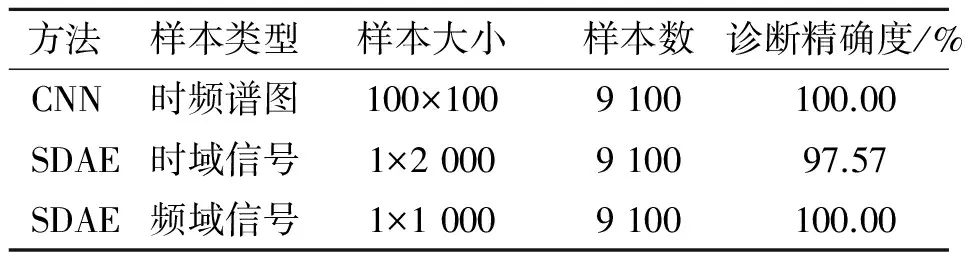
表5 不同深度学习方法的诊断结果

由表5可以看出，以时频谱图为样本时，CNN能够以100%的精确度实现电机故障诊断；以时域信号为样本训练SDAE时，其诊断精确度为97.57%；以频域信号为样本训练SDAE时，其精确度同样可以达到100%。使用SDAE同样可以很好地实现电机故障诊断，但是其样本太小，在实际应用中，样本过小可能导致样本所包含的信息量太少，甚至造成错误样本，从而影响诊断精度。

3.5.3 与连续小波变换结合卷积神经网络的方法的比较

短时傅里叶变换并不是唯一的时频分析方法，为了进一步验证将一维信号通过时频分析转换成图片的方法的有效性，采用连续小波变换(带宽参数和中心频率均为4的复Morlet小波)将原始的振动信号转变为时频图，如图 11所示。同样选取14 000个样本，以20%作为测试集，其余作为训练集，然后将得到的时频图以笔者提出的CNN网络结构和超参数进行训练。

图11 连续小波变换下的各故障样本时频图Fig.11 Time-frequency map by continuous wavelet transform with different fault samples

训练完成后将测试集数据输入模型，同样得到了100%的正确率。试验表明，将一维信号以时频分析方法转换为时频图，再进行CNN网络识别的方法是有效的。

4 结论

1) 以振动信号为基础，提出了基于短时傅里叶变换和卷积神经网络相结合的诊断方法，完成了电机转子、轴承等故障诊断。

2) 较传统方法，本方法降低了对先验知识、信号处理理论和实际经验的需求，同时降低了人工处理信号数据的时间，使得电机故障诊断与预测更加智能化和高效化。

3) 本方法建立在大量样本数据的基础上。样本量大使得样本的多样性得到保证，从而提高网络鲁棒性，也会防止网络过拟合。

4) 本研究的数据集是在特定的试验环境下采集的，与正常工业生产依然存在很大的差异。试验分析时发现，依然存在未学习到特征的卷积核。因此，提高卷积核学习能力，或者是裁剪冗余的卷积核，从而提高网络性能，降低网络复杂度，是一个值得关注的问题。

[1] 沈标正. 电机故障诊断技术[M]. 北京: 机械工业出版社, 1996:88-93.

[2] 康云霞. 基于粗糙集与神经网络的异步电机故障诊断方法的研究[D]. 锦州：渤海大学, 2014.

[3] 李平. 基于多源异类信息融合的异步电机故障诊断技术研究[D]. 湘潭：湖南科技大学, 2013.

[4] Mehrjou M R, Mariun N, Marhaban M H, et al. Rotor fault condition monitoring techniques for squirrel-cage induction machine-A review[J]. Mechanical Systems and Signal Processing, 2011, 25(8):2827-2848.

[5] Cruz Z M A, Cardoso A J M, Carvalho J F S, et al. Rotor cage fault diagnosis in three-phase induction motors by Park′s vector approach[C]∥Coference Record of The IEEE Industry Applications Society Annual Meeting. Orland Florida, USA:[s.n.], 1955:642-646.

[6] Cruz Z M A, Cardoso A J M. Rotor cage fault diagnosis in three-phase induction motors by extend Park′s vector approach[J]. Electric Machines and Power Systems, 2000 ,28(3):289-299.

[7] Cruz Z M A, Cardoso A J M. Stator winding fault diagnosis in three-phase synchronous and asynchronous motors by the extend Park′s vector approach[J]. IEEE Trans on Industry Applications, 2001, 37(5):1227-1233.

[8] 刘振兴, 尹项根, 张哲. 基于Hilbert模量频谱分析的异步电机转子故障在线监测与诊断[J]. 中国电机工程学报, 2003, 23(7):158-161.

Liu Zhenxing, Yin Xianggen, Zhang Zhe. Online monitoring and diagnosis way based on spectrum analysis of Hilbert modulus in induction motors[J]. Proceedings of the CSEE, 2003, 23(7):158-161.(in Chinese)

[9] 方瑞明, 郑力新, 马宏忠,等. 基于MCSA和SVM的异步电机转子故障诊断[J]. 仪器仪表学报, 2007, 28(2):252-257.

Fang Ruiming, Zheng Lixin, Ma Hongzhong, et al. Fault diagnosis for rotor of induction machine based on MCSA and SVM[J]. Chinese Journal of Scientific Instrument, 2007, 28(2):252-257. (in Chinese)

[10] 杨江天, 赵明元. 改进双谱和经验模态分解在牵引电机轴承故障诊断中的应用[J].中国电机工程学报, 2012,32(18):176-122.

Yang Jiangtian, Zhao Mingyuan. Fault diagnosis of traction motor bearings using modified bispectrum and empirical mode decomposition[J]. Proceedings of the CSEE, 2012, 32(18):176-122. (in Chinese)

[11] 钱华明, 王雯升. 遗传小波神经网络及其在电机故障诊断中的应用[J].电子测量与仪器学报, 2009, 23(3):81-86.

Qian Huaming, Wang Wensheng. Improved wavelet neural network based on genetic algorithm and its application in fault diagnosis of motor[J]. Journal of Electronic Measurement and Instrument, 2009, 23(3):81-86. (in Chinese)

[12] 李学军, 李平, 蒋玲莉, 等. 基于异类信息特征融合的异步电机故障诊断[J]. 仪器仪表学报, 2013, 34(1):227-233.

Li Xuejun, Li Ping, Jiang Lingli, et al. Fault diagnosis method of asynchronous motor based on heterogeneous information feature fusion[J]. Chinese Journal of Scientific Instrument, 2013, 34(1):227-233. (in Chinese)

[13] LeCun Y, Boser B, Denker J S, et al. Handwritten digit recognition with a back-propagation network[C]∥Advance in Neural Information Processing Systems. San Francisco, CA: Morgan Kaufmanu Publishers, 1990: 396-404.

[14] Krizhevsky A, Sutskever I, Hinton G E. Imagenet classification with deep convolutional neural network[C]∥ Advances in Neural Information Processing System. Red Hook, NY: Curran Associates, 2012: 1097-1105.

[15] 汪海波, 陈雁翔, 李艳秋. 基于主成分分析和Softmax回归模型的人脸识别方法[J]. 合肥工业大学学报, 2015, 38(6): 759-763.

Wang Haibo, Chen Yanxiang, Li Yanqiu. Face recognition method based on principal component analysis and Softmax regression model[J]. Journal of Hefei University of Technology, 2015, 38(6): 759-763. (in Chinese)

[16] Zeiler M D, Fergus R. Visualizing and understanding convolutional neural networks[C]∥Computer Vision-ECCV 2014.[S.L.]：Spring Internatinal Publishing, 2014:818-833．

[17] 王丽华，陶润喆，张永宏. 基于CEEMD-WPT的滚动轴承特征提取算法[J]. 振动、测试与诊断, 2017,37(1):181-188.

Wang Lihua, Tao Runzhe, Zhang Yonghong. Feature extraction of rolling bearing based on CEEMD-WPT[J]. Journal of Vibration, Measurement & Diagnosis, 2017,37(1):181-188. (in Chinese)

[18] 郝研,王太勇,万剑,等. 基于经验模态分解和广义维数的机械故障诊断[J]. 吉林大学学报:工学版, 2012, 42(2): 392-396.

Hao Yan, Wang Taiyong, Wan Jian, et al. Mechanical fault diagnosis based on empirical mode decomposition and generalized dimension[J]. Journal of Jilin University :Engineering and Technology Edition, 2012, 42(2): 392-396. (in Chinese)

[19] 孙卫祥,陈进,吴立伟,等.基于PCA与决策树的转子故障诊断[J].振动与冲击, 2007, 26(3):72-74.

Sun Weixiang, Chen Jin, Wu Liwei, et al. Rotor fault diagnosis based on PCA and decision tree[J]. Journal of Vibration and Shock, 2007, 26(3):72-74. (in Chinese)

[20] Vapnik V N. The nature of statistical learning theory[M]. New York: Springer-Verlag, 1995：988-999．

10.16450/j.cnki.issn.1004-6801.2017.06.021

国家自然科学基金资助项目(51405241，51505234，51575283)

2017-01-06；

2017-06-27

TH17; TN911