基于TL1范数的改进K-SVD字典学习算法∗

袁 超 李海洋

（西安工程大学理学院 西安 710048）

基于TL1范数的改进K-SVD字典学习算法∗

袁 超 李海洋

（西安工程大学理学院 西安 710048）

K-SVD字典学习算法通过稀疏编码和字典更新两步迭代学习得到训练样本的字典，用OMP（Orthogonal Matching Pursuit）算法求解稀疏表示，用SVD分解算法对字典更新。但应用在图像重构时，OMP算法运行速度比较慢，且恢复的准确度不够高。针对该问题，为了提高字典训练速度与性能，在稀疏编码阶段用TL1范数代替了l0范数，用迭代阈值算法求解稀疏表示。为考察改进算法的恢复准确率，在不同稀疏度下进行数据合成实验，结果表明改进算法比K-SVD算法训练恢复的准确率高。进一步考察改进算法的图像重构能力，选取标准图像进行仿真，实验结果表明改进算法比K-SVD算法能更快得到训练字典，获得更高的峰值信噪比（PSNR），具有更好的重构性能。

字典学习；KSVD；稀疏编码；阈值迭代算法；TL1范数；图像重构

1 引言

近些年，以图像的稀疏先验求解图像重构引起了广泛关注［1～3］。根据压缩感知理论，信号在字典下的表示系数越稀疏则重构质量越高，因此字典的选择十分重要，它决定了图像重构的质量。目前字典构造方法有两种：解析方法和学习方法。基于解析方法构造的字典通过定义好的数学变换或调和分析来构造，字典中的每个原子可用数学函数来刻画，如小波变换、离散余弦变换、轮廓波变换、Shear⁃let等。虽然解析方法构造字典相对简单且计算复杂度低，但原子的基本形状固定，形态不够丰富，因此不能与图像本身的复杂结构进行最佳匹配。基于学习方法是根据图像本身来学习过完备字典，这类字典中的原子与训练集中的图像本身相适应。因此通过学习获得的字典原子数量更多，形态更丰富，能更好地与图像本身的结构匹配，具有更稀疏的表示。

1993 年，Mallat［4］等阐述了过完备字典的概念，并提出了解决过完备字典稀疏表示问题的匹配追踪算法，从而奠定了字典学习理论的基础，但没有给出具体求解字典的方法。1996年Olshausen［5］在《Nature》上发表了Sparsenet字典学习算法，提出了用l1范数作为系数稀疏性度量，这一算法是基于字典学习重构图像的基础，但该算法容易陷入局部最优。为训练全局最优字典，Mailhe［6］等对Olshausen的算法进行了改进，将梯度下降中的固定步长改为自适应步长，从而越过局部最优点，最终以较大的概率保证在全局最优点收敛。Engan［7］也对Sparsenet字典学习算法进行了改进，提出了MOD（Method of optimal directions）字典学习算法。MOD算法采用l0范数衡量信号的稀疏性，利用交替优化求解字典。该算法的缺点是需要进行矩阵的求逆计算，对存储容量的要求高。

为减小 MOD算法的复杂度，2006 年 Elad［8］等提出了 K-SVD（K-singular value decomposition）字典学习算法，实现了基于K-SVD字典学习的图像重构，K-SVD字典学习是一种交替迭代算法，首先固定当前字典稀疏编码求解稀疏表示系数，然后根据稀疏系数对字典的列进行迭代更新。K-SVD算法更新字典时不是对整个字典一次更新，而是逐个原子更新。该算法不需要矩阵求逆计算，运算复杂度比MOD算法低，并且在字典更新步骤中对系数矩阵与字典原子联合更新，提高了算法收敛速度。K-SVD算法在实际中有广泛应用，随后许多 学 者 对 其 进 行 了 改 进 ，Rubinsteind［9］用Batch-OMP替代OMP稀疏编码，比K-SVD字典训练效率更高，但图像重构效果却有所下降。Smith［10］在字典更新中加入了支撑的先验信息，提出了MDU多重字典更新算法，有效地减小了字典学习的目标函数，但训练计算量较大。

当前字典学习存在的主要问题是训练时间长，恢复的准确度不够高。针对这一问题，为提高字典学习的速度与性能，本文在稀疏编码阶段用TL1范数代替l0范数，用迭代阈值算法求解稀疏表示，提出TL1-KSVD字典学习算法。事实上，早在2000年Nikolola［11］在 研 究 变 量 选 择 时 定 义 了 TL1范 数（transformedl0penalty），2009 年 Lv［12］研究了 TL1范数的稀疏性，2014年 Xin［13～14］等把 TL1范数应用到压缩感知，并给出了TL1范数的阈值迭代算法。

2 K-SVD字典学习模型

假设给定训练图像Y∈RN×L包含 L个信号，字典学习的实质是找到恰当的未知字典 D∈RN×M（N＜M）并使得每个信号 yi可用字典D∈RN×M稀疏表示，其模型为

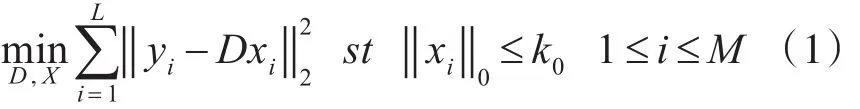
2.1 稀疏编码

在该阶段，固定字典D，寻找训练样本Y在字典D上的稀疏表示系数X。稀疏表示的重构称为稀疏编码，训练样本Y上每一个信号 y∈RN可用字典D的原子线性表示。其稀疏表示模型［15］为

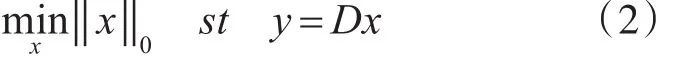
其中 D∈RN×M（N＜M）是一个字典，是 x∈RM稀疏的，式中：‖‖x0是为x中非零的个数。

可以使用贪婪追踪算法求解问题（2），如正交匹配追踪（OMP）［17～18］，但需要将原始信号内的元素逐一稀疏表示，但OMP算法收敛速度较慢，且图像重构质量差。求解问题（2）的精确解是一个NP［16］难问题，而且对噪音非常敏感。压缩感知理论指出，如果观测矩阵D满足约束等距RIP［3］（Restrict⁃ed Isometry Proper）性质，则可高概率重构原始信号x，即：

式中，δk∈(0，1)称为 RIP常数。

Donoho等［19］提出利用 l1范数代替 l0范数，变成线性规划的凸优化问题，找出最稀疏的系数矩阵。其模型为

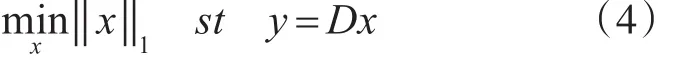
式中：‖‖x1为x中元素的绝对值之和。

解决问题（4）可以通过无约束凸优化问题近似求解，模型为

转化为无约束凸优化求解l1范数问题。使用基 追 踪（BP，Basis Pursuit）［20］，FOCUSS［21］，LARS-Lasso［22］等算法求解，或者利用软阈值截取运算（Soft-thresholding）［23］求解。然而基于 l1范数的求解稀疏表示至少仍存在两个方面的不足：第一，图像信号之间可能存在冗余难以去除；第二，无法区分稀疏尺度的位置。相关研究表明，用1/2范数等非凸函数代替l0范数时，有更好的效果。

2.2 字典更新

在字典更新阶段应用SVD的更新字典［6］，固定稀疏系数X，对字典D中的原子按列进行迭代更新。

3 基于TL1-KSVD的字典学习

我们仍把它称作范数。另外因为满足以下性质：

1）ρ(x)递增且在x∈[0，∞ )是凹的。

2）ρ′(x )在 ρ′(0 +)∈(0 ，∞ )是连续的。

因此‖*‖TL能产生稀疏的效果。

用TL1惩罚项代替式（5）中的l1惩罚项，则式（5）模型变为

为了求解优化问题（6），J Xin等在文献［25］中提出用阈值迭代算法，算法的迭代格式为

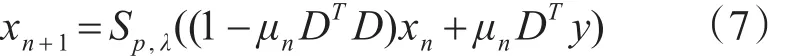
式中：xn为第 n 次近似值，μn为参数，Sp，λ:RN→RN是由特定的阈值函数诱导出的对角非线性阈值算子。并给出了该问题的阈值迭代函数，其阈值迭代函数如下

式中：

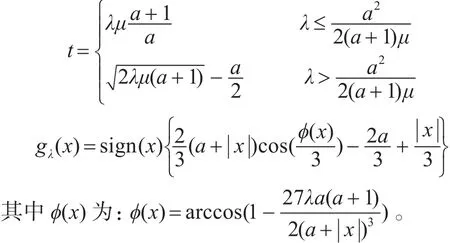
3.1 稀疏编码

为了缩短稀疏编码时间，提高字典训练速度和性能，引入速度较快的阈值迭代算法解决问题（6），算法流程如算法1所示。

算法1 基于TL1阈值迭代函数的稀疏编码

输入：信号Y∈RN×L，字典 D∈RN×M

初始化：x0，给一个合适的a，ε，μ0；

迭代步骤1：计算 zn=Bμ(xn)=xn+μDT(y-Dxn)，令 λ=λ0，μ=μ0；

3.2 字典更新

在字典更新阶段应用SVD的更新字典［8］，固定稀疏系数X，对字D中的原子按列进行迭代更新，字典列的更新结合稀疏表示的一个更新，使字典和稀疏系数同步更新。字典更新过程可表示优化模型：

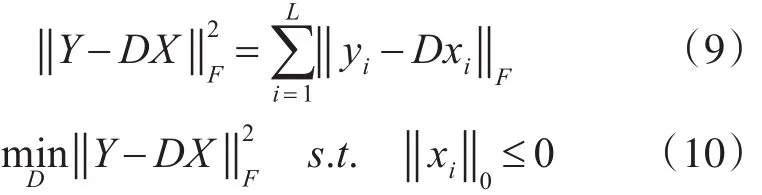
式中：‖‖xi0是计算xi中非零元素的个数：

通过对Ek进行SVD分解得到秩为1的矩阵近似值用于更新原子dk和稀疏表示对应的系数，同步更新大大加速了训练算法的收敛速度。基于TL1-KSVD的字典学习算法的步骤，如算法2所示。

算法2 基于TL1-KSVD的字典学习算法

输入：训练样本集Y∈RN×L

迭代步骤1初始化字典：赋初始值给字典D；

2稀疏编码：根据已知字典D，运用算法1求解样本Y的稀疏系数X；

3字典更新：根据稀疏系数 X，更新字典D。设为dk要更新的字典D的第k列原子，Ek代表抽取字典原子dk后的误差矩阵。定义分解用到原子dk时所有 yi的索引集合。则：Ek=Y-(DX-dkxk)；

选取仅与ωk相关的列约束Ek，得到Eωkk，对其进行奇异值分解（SVD），更新 dk=u1，xk=∆(1，1)·v1；

输出：学习字典D，稀疏表示系数X。

4 实验结果及分析

为了验证本文算法重构性能，对本文算法与K-SVD算法进行数据合成实验和图像重构实验对比分析。利用CPU为4GHz，内存为16GB的计算机，通过Matlab R2010a仿真实现。实验图像为512×512像素，图像分块为8×8，字典大小为64×256。

采用字典训练时间、用峰值信噪比（PSNR）和图像的重构成功率作为衡量两个算法性能评价标准。峰值信噪比（PSNR）：

其中MSE是原图像与压缩重建后图像之间的均方误差。图像的重构成功率：Aharon提出了计算成功恢复的准则，这个准则是为了计算两个正则化元素之间的距离。用di来表示原始矩阵的第i列，di来表示重构矩阵的第i列。如果1-|＜0.01，可以认为矩阵的第i得到了成功恢复。实验图像为512×512像素，图像分块为8×8，字典大小为64×256。下面列出了图像的实验结果对比。

4.1 数据合成实验

为了验证本文算法的成功恢复率，在不同稀疏度下反复实验。并在相同稀疏度下与K-SVD算法的重构效果进行比较。实验中，用标准的Lena图像进行采样重构，以加权的高斯随机矩阵作为观测矩阵，稀疏度K从10开始，每次增大5，用两种算法对每个稀疏度K各进行100次实验比较，并对求其平均值，实验结果如图1所示。

实验分析：随着稀疏度的增大，两种算法的重构成功率逐渐减小。与OMP算法相比，当稀疏度较大时本文算法有着较为明显的优势（如稀疏度K在40时，本文算法仍能恢复出原图）。本文算法在重构成功率上也有较大程度的提高，稀疏度K在20～35之间，其优势更为凸显，比OMP重构算法提高了6.8%～56.8%。

图1 K-稀疏信号重构准确率

4.2 图像重构实例

为了考察本文算法重构时间与重构效果，在不同采样率下反复实验，并在相同采样率下与K-SVD算法的重构时间与重构效果进行比较。对Lena图像和peppers图像进行8×8的分块，以高斯随机矩阵作观测矩阵，最后对每个分块图像进行重构恢复。

实验中分别在0.4，0.6，0.8不同采样率下进行测试。在同一采样率下对每种算法反复进行150次试验，获得峰值信噪比PSNR值和运行时间，并对求其平均值，其测试结果，如表3、表4所示。

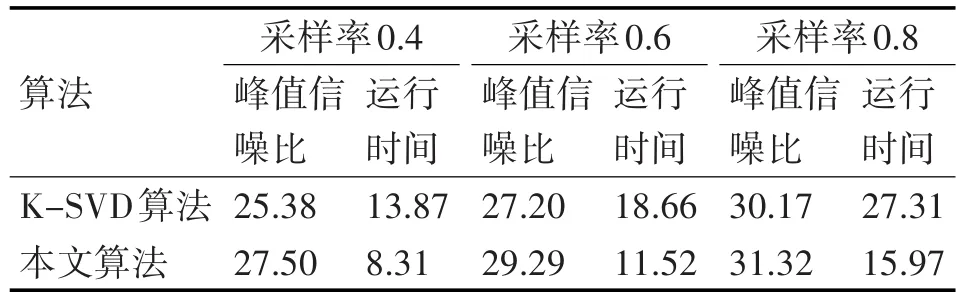
表3 Lena图像在不同采样率两种算法PSNR值和运行时间比较

表4 peppers图像在不同采样率两种算法PSNR值和运行时间比较

实验分析：通过表3可以看出，在相同稀疏度时，随着采样率的增大，两种算法的PSNR值均相应增大，且在不同采样率下本文算法的PSNR值较K-SVD算法均有较大程度的提高，在较小采样率下效果尤为明显，在采样率为0.4时提高了2.12dB。同时，本文算法的运行速度也有了较大程度的提高，采样率在0.4，0.6，0.8对比K-SVD算法提高了5.56s、7.14s、11.34s。表明随着采样率增大，本文算法的运行速度的增幅相对于K-SVD算法的运行速度的增幅越来越大。

二维图像的重建仿真源图像为512×512的Le⁃na图和peppers图，分别基于K-SVD算法和本文算法进行恢复重构，其重构结果如下图所示，可见不同的采样率下，本文算法重构效果都好于K-SVD算法的重构效果。如图2所示。

图2 二维图像的重建仿真

5 结语

针对于K-SVD在图像重构中所存在的恢复准确度不够高以及稀疏编码时间过长的问题，本文提出了基于TL1范数的改进的K-SVD字典学习模型。首先本文建立非凸极小化模型，提出了改进的字典学习算法，该方法利用非凸‖*‖TL范数求得的1稀疏表示，提升了字典训练速度与性能。其次图像重构实例结果表明与K-SVD字典学习算法相比，本文算法稀疏编码速度更快，恢复的准确度更高，重构效果更好。由于完备字典的训练时间过长，因此如何训练更快速、更有效的字典是下一步工作的内容。

［1］Dong Wei-sheng，Zhang Lei，Shi Guang-ming，et al.Non⁃locally centralized sparse representation for image restora⁃tion［J］.Image Processing，IEEE Transactions on，2013，22（4）：1620-1630.

［2］Yang M，Zhang L，Feng X，et al.Fisher Discrimination Dictionary Learning for sparse representation［C］//IEEE International Conference on Computer Vision，ICCV 2011，Barcelona，Spain，November.DBLP，2011：543-550.

［3］Candes E J，Romberg J，Tao T.Robust uncertainty princi⁃ples：exact signal reconstruction from highly incomplete frequency information［J］.IEEE Transactions on Informa⁃tion Theory，2006，52（2）：489-509.

［4］Mallat S，Zhang Z.Matching pursuits with time-frequen⁃cy dictionaries［J］.IEEE Transactions on Signal Process⁃ing，1993，41（12）：3397-3415.

［5］Olshausen B A，Field D J.Emergency of simple-cell re⁃ceptive field properties by learning a sparse code for natu⁃ral images［J］.Nature，1996，381（6583）：607-609.

［6］Mailhé B，Plumbley M D.Dictionary learning with large step gradient descent for sparse representations［C］//In：Proceedings of the 10th International Conference on La⁃tent Variable Analysis and Signal Separation.Berlin，Hei⁃delberg：Springer，2012.231-238.

［7］Engan K，Aase S O，Husoy J H.Method of optimal direc⁃tions for frame design［C］//IEEE International Conference on Acoustics，Speech，and Signal Processing，1999.Pro⁃ceedings.IEEE，1999：2443-2446 vol.5.

［8］Aharon M，Elad M，Bruckstein A M.The K-SVD：an algo⁃rithm for designing of over complete dictionaries for sparse representation［J］.IEEE Transactions on Signal Process⁃ing，2006，54（11）：4311-4322．

［9］Rubinstein R，Zibulevsky M，Elad M.Efficient implemen⁃tation of the K-SVD algorithm using batch orthogonal matching pursuit［J］.CS Technion，2008，40（8）：1-15．

［10］Smith L N，Elad M.Improving dictionary learning：Multi⁃ple dictionary updates and coefficient reuse［J］.Signal Processing Letters IEEE，2013，20（1）：79-82．

［11］NIKOLOVAM.Local strong homogeneity of a regularized estimator［J］.SIAM J Appl Math，2000，61（2）：633-658.

［12］Lv J，Fan Y.A unified approach to model selection and sparse recovery using regularized least squares［J］.An⁃nals of Statistics，2009，37（6A）：3498-3528.

［13］Zhang S，Xin J.Minimization of Transformed$L_1$Pen⁃alty：Closed Form Representation and Iterative Thresh⁃oldingAlgorithms［J］.Mathematics，2014.

［14］S Zhang，J Xin.Minimization of Transformed L1 Penalty：Theory Difference of Covex Function Algorithm，and Ro⁃bust Application in CompressedSensing［EB/OL］.Eprint⁃Arwiv，2016.https：//arxiv.org/abs/1411.573.

［15］BrucksteinA M，Donoho D L，Elad M.From sparse solu⁃tions of systems of equations to sparse modeling of sig⁃nals and images［J］.SIAM Review，2009，51（1）：34-81.

［16］Donoho D L，Elad M，Temlyakov V N.Stable recovery of sparse over complete representations in the presence of noise［J］.Information Theory，IEEE Transactions on，2006，52（1）：6-18．

［17］Mallat S G，Zhang Z.Matching pursuits with time-fre⁃quency dictionaries［J］.Signal Processing，IEEE Trans⁃actions on，1993，41（12）：3397-3415．

［18］Tropp J.Greed is good：Algorithmic results for sparse ap⁃proximation［J］.Information Theory，IEEE Transactions on，2004，50（10）：2231-2242．

［19］Donoho D L.For most large underdeterzmined systems of linear equations the minimal 1-norm solution is also the sparsest solution［J］.Communicationson Pure and Ap⁃plied Mathematics，2006，59（6）：797-829．

［20］Chen S S，Donoho D L，Saunders M A.Atomic decompo⁃sition by basis pursuit［J］.SIAM Journal on Scientific Computing，1998，20（1）：33-61.

［21］Gorodnitsky I F，Rao B D.Sparse signal reconstruction from limited data using FOCUSS：A re-weighted mini⁃mum norm algorithm［J］.Signal Processing，IEEE Trans⁃actions on，1997，45（3）：600-616．

［22］Efron B，Hastie T，Johnstone I，et al.Least angle regres⁃sion［J］.The Annals of Statistics，2004，32（2）：407-499.

［23］戴琼海，付长军，季向阳.压缩感知研究［J］.计算机学报，2011，34（3）：425-434.DAI Qionghai，FU Changjun，JI Xiangyang.Research on compressed sensing［J］.Chinese journal of computers，2011，34（3）：425-434.

［24］S Zhang，J Xin.Minimization of Transformed L1 Penalty：Closed Form Representation and Iterative Thresholding Algorithms， Mathematics， 2016https：//arxiv.org/abs/1412.5240.

K-SVD Dictionary Learning Algorithm Based on TL1Norm

YUAN Chao LI Haiyang
（School of Science，Xi'an Polytechnic University，Xi'an 710048）

K-SVD dictionary learning algorithm is employed to obtain the training dictionary by using sparse coding and dic⁃tionary updating iteratively，in which Orthogonal Matching Pursuit algorithm（OMP）is used to get the sparse expressions in the sparse coding stage，while the SVD algorithm is utilized to update the dictionary.However，when it is applied into the image recon⁃struction，the Orthogonal Matching Pursuit algorithm（OMP）is slower and its accuracy is not satisfied.Aiming at this problem，To improve the speed and performance of training dictionary，l0is replaced with TL1in the sparse coding stage，and the iterative thresh⁃old algorithm is used to the sparse expressions.To test the performance of the proposed algorithm，date synthesis experiment is con⁃ducted under different sparse degree，and these results show that the proposed algorithm is better than the K-SVD.To further test the performance of the proposed algorithm，the standard image is used to simulate and the experimental results show that the pro⁃posed algorithm is faster than K-SVD to obtain the training dictionary，and has higher PSNR and better reconstruction performance.

dictionary learning，K-SVD，threshold iterative algorithm，TL1norm，image reconstruction

Class Number TP301.6

TP301.6

10.3969/j.issn.1672-9722.2017.12.001

2017年6月5日，

2017年7月23日

国家自然科学基金项目（编号：11271297）；陕西省自然科学基金项目（编号：2015JM1012）资助。

袁超，男，硕士研究生，研究方向：图像处理，机器学习。李海洋，博士，教授，研究方向：稀疏信息处理，量子逻辑及格上拓扑学。