老师课堂“导”什么

孙广武

施教之功，贵在引导，妙在开窍。教师在教学中的主要任务不是教，而是导，是指导学生学，引导学生由学会到会学。这就需要教师转变观念，转换角色，恰当处理教与导的关系，变教为导。教师導好了，学生就能开窍。因此，教师应该在导上下功夫。

导出隐含在教材中的解题方法。教材上呈现的解题方法是一些基本的、通用的方法。但是，教材上没有直接写出来，要靠教师读懂教材，引导学生理解并掌握，同时更需要教师点破方法这层纸。教师只有点破了，学生才会认识到某种方法的重要性，进而引起关注。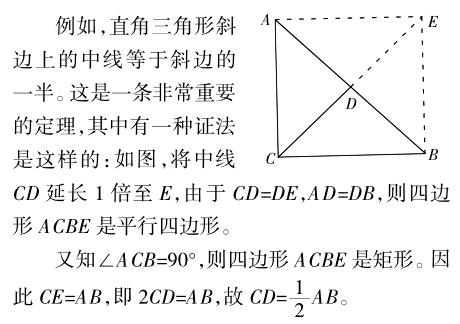

教学时，老师们一般是到此为止。这里，教师没有导出“将中线延长1倍”的价值。上述证法提供了证明一条线段是另一条线段2倍的方法：或者将短线段延长1倍，或者将长线段取半。这一点，教师如果不导，学生一时是难以体会到的，也就无法掌握定理证明中所蕴含的证题方法。

导出教材隐含的数学知识。教材不可能包罗万象，不能将所有的知识都罗列出来。有许多与教材紧密相关的知识需要教师导出来，而导出来的知识往往是很鲜活的，最能考察学生灵活运用知识的能力。

例如，椭圆的定义是：动点到两定点的距离和是定值；双曲线的定义是：动点到两定点的距离差是定值。动点到定点的距离的和、差都学了，有没有商或积为定值时，动点的轨迹是特殊图形呢？提出这样的问题很有价值，学生完全可以做一做。不难发现，动点到两定点的距离商是定值时，动点的轨迹是圆。这个圆叫做阿波罗尼圆。高考题中就有许多涉及阿波罗尼圆的考题。命题者也许就是根据椭圆、双曲线的定义类比出来的。这些考题很多，举两例供读者参考。endprint