一种提高铁路安全通信的混沌加密新方法

蒋逢灵 谭 文

1(湖南铁路科技职业技术学院 湖南 株洲 412006) 2(湖南科技大学信息与电气工程学院 湖南 湘潭 411201)

一种提高铁路安全通信的混沌加密新方法

蒋逢灵1谭 文2

1(湖南铁路科技职业技术学院 湖南 株洲 412006)2(湖南科技大学信息与电气工程学院 湖南 湘潭 411201)

现有铁路安全通信协议RSSP(Railway Signal Safety Protocol)，对保障铁路安全通信具有非常重要的作用，但是因攻击者的攻击而存在安全隐患，对铁路的安全通信造成威胁。基于混沌信号的独有特性，提出一种保障铁路安全通信的混沌加密方法。结合混沌掩盖技术，把传送信号经过加密函数混合到混沌信号中，经过混合的信号类似杂波信号，达到不易被破解与攻击的目的。利用分数阶超混沌系统的同步信号对混合信号通过解密函数去掩盖，大致经过6.2 s把铁路通信需要传送的信息从混合信息中恢复出来，实现了铁路的安全通信。数值仿真和理论分析结果的一致性表明了该方案的有效性。

分数阶超混沌系统 同步控制 安全通信

0 引 言

中国列车控制系统CTCS(Chinese Train Control System of Level)经过多年的发展，运行速度快，运行时间长，通信安全级别高，其通信数据的安全可靠，直接影响到列车的安全运行。我国铁路通信传输系统的通信安全主要是基于铁路安全通信协议RSSP，利用防火墙技术，通过数据加解密算法、密钥认证、安全数据库等技术对付来自外围环境的攻击、数据流、病毒防护等安全维护[1-2]。随着CTCS-3第三代列车控制系统的发展，运行速度高达300 km/h及以上，通信安全要求更高。这种CTCS-3列控的通信方式，与之前CTCS列控通信方式相比，采用无线闭塞中心RBC(Radio Blocking Center)，以GSM-R(GSM for Railway)通信技术利用铁路通信协议RSSP及其相关安全协议的安全保障进行数据通信，实现数据的安全传送。虽然这种利用铁路通信协议的通信方式，可以确保铁路通信的安全，但是易受到外部的攻击，对数据的传送存在安全隐患，使得铁路安全通信存在潜在的风险。文献[3]针对铁路安全通信协议RSSP-Ⅰ和RSSP-Ⅱ，深入分析了两种铁路通信协议在铁路通信传输范围、要求及功能上优势各异，但都存在安全缺陷，不利于铁路通信数据的安全传输，具有潜在危险。郭伟等[4]利用生日攻击原理，对RSSR-Ⅱ协议的核心消息鉴别码MAC密钥防护技术，提出了一种部分密钥恢复-伪造攻击方案。通过攻击示例在有限长的时间内，攻击者通过已知明文的情况下，可以恢复密钥，并且攻击成功率高达63%，暴露出RSSP-Ⅱ协议的漏洞。张元玲等[5]提出了一种通过改进MAC算法在ER层中的方法对铁路安全通信进行高级加密，虽然提高通信的安全性，但是攻击者可能采用选择性伪造获得传送消息的MAC值。

然而，混沌信号具有伪随机性、无规律、类似噪声的特点[6]，在自然界中往往被误认为杂波信号而容易被忽视。分数阶超混沌系统比低维混沌系统的动力学轨迹行为更加复杂丰富，密钥空间拓扑性优势更强[7]，非常适合安全保密通信的应用[8-10]，对信息的传输极具隐蔽性。混沌信号用作信息传送的密钥，它的关键问题是要解决混沌系统之间的同步，驱动系统作为信号传送的加密密钥，其相应的响应系统作为信息解码的密钥。

本文基于分数阶系统稳定性理论，研究分数阶Lorenz超混沌系统之间的同步控制问题。通过设置合适的控制器，将分数阶超混沌系统的同步转化成分数级超混沌系统误差系统的稳定性分析。通过求解特征值的方法作为判定分数阶超混沌系统之间的同步方法。这种方法不需要计算Lyapunov指数，简化了实现同步的方法。最后利用分数阶超混沌信号的独有特性和同步控制，提出了一种提高铁路安全通信的混沌加密方法，在铁路现有的RSSP-Ⅱ安全通信协议的基础上，不改变铁路通信系统现有信息交换方式。通过数据混沌加密的方式保障通信数据的安全，以分数阶超混沌驱动系统的信号作为传送信号的载体，结合混沌掩盖技术将传送信息通过加密函数加密到混沌信号中，在传送信道里以混合信息传送。而这种经过混合的信号类似杂波信号，攻击者因无法获得相应响应系统的同步信号而难以攻击与破解，从而实现信息的安全有效传送。

1 分数阶微分及其逼近

关于分数阶微分的理论现存版本较多[11]，就不过多赘述，本文选择Caputo提出的经典理论：

(1)

式中：n为不小于α的第一个整数，Jβ为β阶Riemann-Liouville积分算子，其表达式：

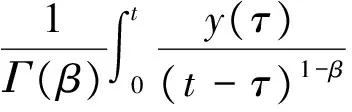
(2)

这里Γ(·)是伽马函数，0<β≤1。

假设分数阶混沌系统表达式为：

(3)

式中：X1∈Rn×1，q为系统的阶数。

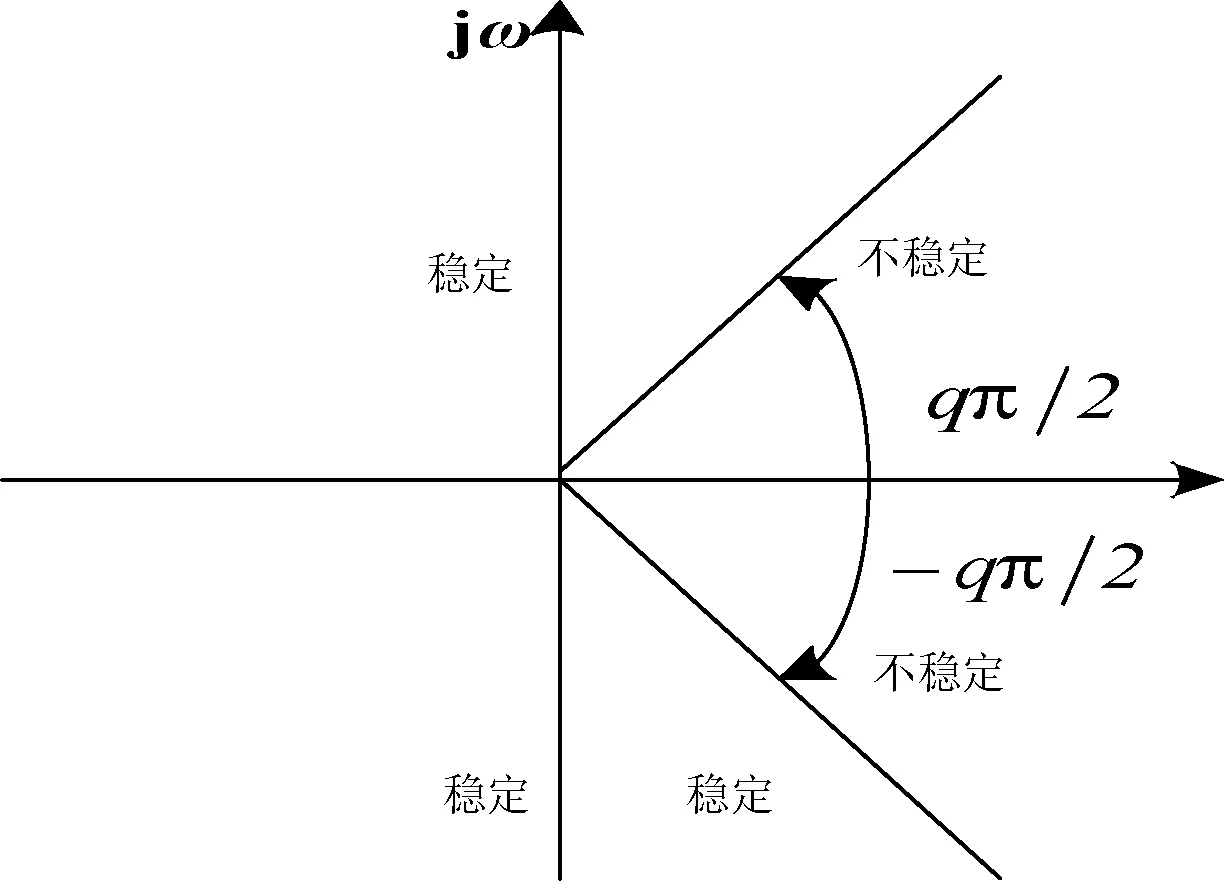
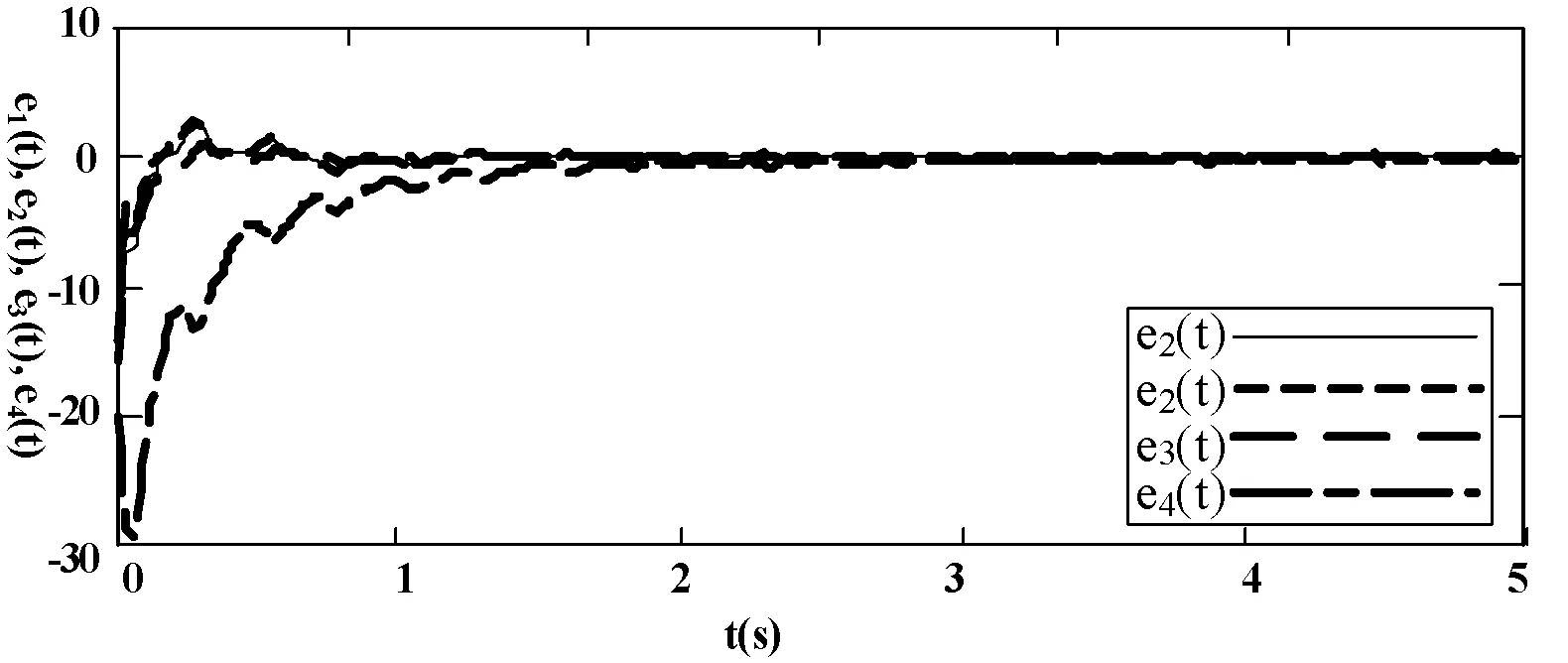
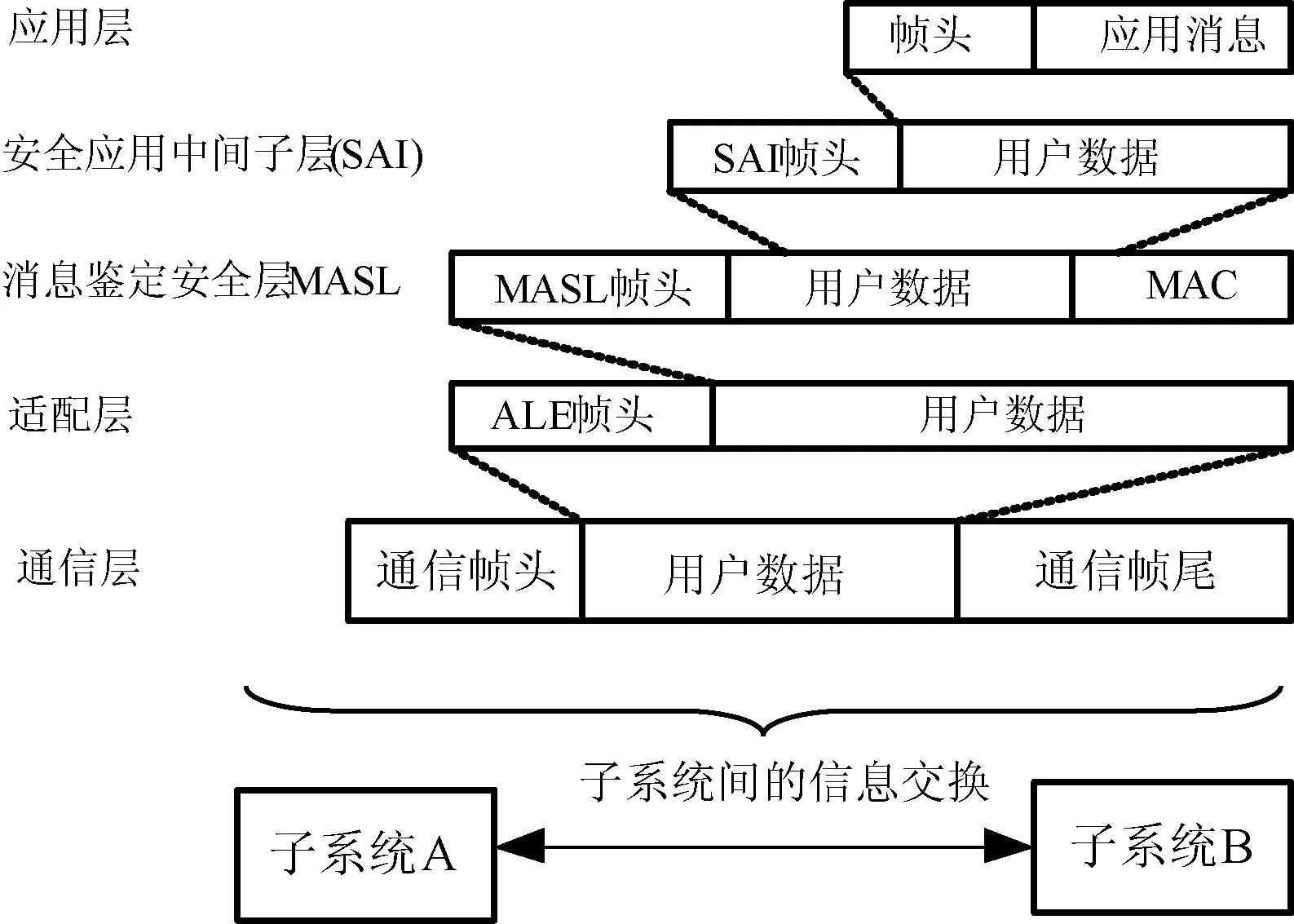
F(X1)=(f(X1)，f(X2)，…，f(Xn))T，0

F(X1)=0

(4)

得到其响应系统为：

(5)

式中：X2∈Rn×1，u(t)为控制函数。定义误差函数e(t)=X1(t)-X2(t)，则得到分数阶误差系统为：

(6)

文献[12]论证了分数阶系统稳定的充要条件，可以将分数阶系统的同步问题转化为判定分数阶误差系统的稳定分析。在应用此方法之前，引入一个重要的引理。

图1 分数阶系统的稳定性区域

推论1整数阶混沌系统是稳定的，那么它相对应的分数阶混沌系统必定渐进稳定。

2 分数阶Lorenz超混沌系统

Lorenz系统与Chen系统、Lü系统称为为广义Lorenz混沌系统，很多研究者都非常关注这三个系统的混沌行为、动力学表现特性、同步控制及其应用。本文研究经典分数阶Lorenz超混沌系统之间的同步具有典型的代表性意义，其数学表达式为：

(7)

式中：α是系统式(7)的阶数(0<α<1)，x、y、z和w为系统变量，a、b、c、d和r系统参数。

数值仿真，参数a=35,b=8/3,c=28,r=-1，α=0.97。系统表现出了混沌行为，存在混沌吸引子相图如图2所示。说明当α=0.97时，系统式(7)是3.88阶分数阶超混沌系统出现了混沌行为。

图2 分数阶超混沌Lorenz系统的吸引子

关于分数阶超混沌系统同步有多种方法，较为常见的通常是在分数阶混沌系统x、y、z、w中分别添加控制函数u1、u2、u3、u4。虽然这种方法可以实现系统之间的同步，但是造成系统的结构复杂，影响某些工程上的应用。其中有些非线性相关项并不影响系统的稳定性。这里只在系统(7)中的y相、z相和w相中分别添加控制函数u1、u2、u3，这样可以简化系统的结构，则得到相应响应系统方程 ：

(8)

根据前面的理论分析和推论1，引入误差函数：

(9)

将系统式(7)与系统式(8)的同步问题转化到其误差系统的稳定性分析中，将式(7)减式(8)，得到分数阶误差动态系统：

(10)

由式(10)可知，只要定义合适的控制函数，系统式(10)是渐进稳定的，则系统式(7)与系统式(8)是可以实现同步的。这里给出定义控制函数为：

(11)

式中：k取正常数。

由式(11)和式(10)可得：

(12)

根据分数阶系统稳定性判定方法，当t→∞时，lime(t)=0，则能判定系统(12)将渐渐趋向于稳定。

为了求得系统式(12)的特征值，将分数阶误差系统对应整数阶系统进行线性化，求得整数阶系统的雅克比矩阵为：

(13)

根据det[λI-A]=0，计算系统的特征根，则得：

D= det[λI-A]=

(14)

将式(7)特征值求解进一步计算，则：

(λ+a)×(λ+k)3=0

(15)

显而易见，由式(15)可求出整数阶系统的特征根为-a、-k。当a和k取一个正常数时，矩阵A的特征根λ<0，根据推论1可以判定分数阶误差系统是稳定的。当t→∞时，分数阶误差系统趋于零，因此可以判定系统式(7)与系统式(8)实现同步。为了验证判定方法的正确性，在Matlab软件中进行数值仿真，通过虚拟示波器观察输出误差系统的曲线。设置系统的参数a=35,b=8/3,c=28,r=-1，α=0.97，k=2。赋值驱动系统式(7)的参数值，设置其初始值为x1(0)=y1(0)z1(0)=w1(0)=10，响应系统式(8)初始值为x2(0)=y2(0)z2(0)=w2(0)=10，得到误差系统大约经过2.8 s均趋于零，如图3所示。

图3 系统(7)与系统(8)的同步误差曲线

3 铁路安全通信的混沌加密方法

为了保障我国CTCS-3级列车通信的安全，采用的专用移动通信系统GSM-R在实际运行中暴露出了安全问题，难以满足通信的要求[15-16]。为此，参考欧洲列车控制系统ETCS(Europe Train Control System)标准[17]，制定了RSSP-Ⅱ通信协议标准及其相关标准，利用协议中安全功能模块提供安全服务如图4所示。

图4 安全协议结构图

其中安全模块中的消息鉴定层和安全应用中间子层是整个通信安全保障的核心，对铁路的通信安全至关重要，如图5所示。消息鉴定安全层中的消息鉴定码作为通信系统的重要密码，信息交换的接受方还是发送方都必须依靠此密码进行数据交换，它们共用一个相同的MAC算法，信息交换必须得到密钥的同步。这样敌手，也就是所谓的攻击者就难以获得密钥，从而难以破坏通信系统的安全。但是敌手的攻击条件如果采用已知明文攻击、选择性攻击和自适应攻击，会获得相应的MAC值，对发送者和接受者数据的传送构成威胁。更为严重的是，一旦敌手在已经明文的条件下，在允许运算范围内采用通用性伪造或密钥恢复攻击目标，则对通信系统构成致命威胁。

图5 RSSP-Ⅱ协议中定义的消息结构

混沌加密的方法是利用混沌信号伪随机、非周期、类似噪声的特性，在RSSP-Ⅱ协议的安全功能模块中进行数据的加密传送，给通信系统多增加了一道安全防护。数据传送通过MAC值进行密钥认证作为发送方和接收方建立通信的基础，而混沌加密则把数据再一次加密保护，在数据的源头上保护信息的安全。即便敌手通过攻击目标恢复密钥，也不会影响数据信息的安全。加上混沌信号对初值极度敏感，初始值发生轻微变化，系统产生的混沌行为差异巨大，攻击者无法获得同步信号，因此不能破解数据的加密，对通信的安全不能造成任何威胁。文中研究的混沌加密方法不改变铁路安全通信协议，结合RSSP-Ⅱ协议中定义的消息结构图，其混沌加密的方式款图如图6所示。

图6 混沌加密示意图

从图6混沌加密示意图可知，子系统A与子系统B之间的信息交换协议没有发生改变，还是在RSSP-Ⅱ通信协议的基础上。只是在信息传输的过程中引入了混沌加密的新加密方法，传送信号在传送过程中，与混沌信号经过加密函数加密后以混合信号的方式进行传送，最后在接受方利用同步信号经解密函数解密后恢复传送数据到达子系统B。

为了进一步验证理论分析的正确性，选择一组数据作为传送信号，本文选择幅度为2，周期为1 s的正弦信号作为传送数据s(t)如图7所示，这种周期性信号安全级别极低，非常容易被攻击者破解。根据图6混沌加密的示意图的方法，将s(t)信号通过加密函数与系统(7)的混沌信号x1(t)混合后，以混合信号m(t)进行传播如图8所示。经过加密函数混合后的信号与之前的传送信息完全不同，幅值与频率发生了颠覆变化，与图7之前的周期性信号完全不一样，从表面上看类似杂波信号，攻击者因为无法获得混沌同步信号的密钥难以攻击与破解，提高了信息传送的安全性。

图7 传送信息

图8 混合信息

信息传送到达子系统B之前，必须通过密钥进行数据的恢复，利用系统(8)的同步信号x2(t)通过解密函数把混合信号解密后获得原始信息如图9所示。由图9可知，大约经过6.2 s后把原始信息毫无失真地恢复出来了传送到子系统B中。

图9 恢复信号与原信号

数值仿真结果验证了混沌加密方法在铁路通信中应用的理论分析，并且不用改变现有通信协议，只是在两个系统之间利用混沌函数产生的混沌信号加密进行信息传送。

4 结 语

铁路通信的安全性直接关系到铁路的正常运营。现有的RSSP协议在保证铁路通信安全确实发挥了重要的作用，但是因为攻击者对目标的攻击有可能确定传送消息的MAC值或者通过目标攻击恢复密钥，对铁路安全通信构成严重的威胁。因此，针对RSSP协议存在的安全隐患，利用混沌信号其独有的特性，提出了一种提高铁路安全通信的混沌加密新方法。把所需传送的有用信号掩盖在混沌信号中进行传播，以混沌信号的方式进行传播类似杂波信号，起到很好的掩盖作用。从理论上杜绝攻击者的攻击，有效地保障了铁路通信的安全传送，从而提高了铁路通信的安全性。数值仿真和理论分析结果的一致性表明了该方案的有效性。实际应用中，可以利用混沌信号发生器产生混沌信号加密到数据信息中，也可以在通信安全系统中嵌入混沌电路的方式直接与传送数据信息进行加密。

[1] 周宏伟,张涛,苗长俊.高速铁路信号技术[M].北京:中国铁道出版社,2012.

[2] 孔冰之.铁路信号安全通信密钥管理系统的设计与仿真[D].成都:西南交通大学,2015.

[3] 周宏伟,张涛,苗长俊.RSSP-Ⅰ与RSSP-Ⅱ铁路安全通信协议对比分析[J].铁道通信信号,2013,49(1):76-78.

[4] 郭伟,闫连山,王小敏,等.RSSP-Ⅱ铁路信号安全通信协议的安全性分析[J].铁道学报,2016,38(8):50-56.

[5] 张元玲,徐中伟,万勇兵,等.铁路信号安全通信协议中的MAC改进算法[J].计算机工程,2012,38(3):246-248.

[6] 方锦清.驾驭混沌与发展高新技术[M].北京:原子能出版社,2002.

[7] Deng Y S,Qin K Y.Fractional Order Liu-system Synchronization and Its Application in Multimedia Security[C]//International Conference on Communications,Circuits and Systems.IEEE,2010:769-772.

[8] 张志明,张一帆,王瑜.基于分数阶控制器的分数阶混沌系统同步[J].兰州理工大学学报,2016,42(4):52-158.

[9] 李震波,唐驾时.参数扰动下的混沌同步控制及其保密通信方案[J].控制理论与应用,2014,31(5):592-600.

[10] 薛薇,徐进康,贾红艳.一个分数阶超混沌系统同步及其保密通信研究[J].系统仿真学报,2016,28(8):1915-1928.

[11] Podlubny I.Fractional differential equations[M].New York:Academic Press,1999.

[12] Matignon D.Stability Results For Fractional Differential Equations With Applications To Control Processing[J].Computational Engineering in Systems Applications,1996,2:963-968.

[13] 胡建兵,韩焱,赵灵冬.基于Lyapunov方程的分数阶混沌系统同步[J].物理学报,2008,57(12):7522-7526.

[14] 孙宁,张化光,王智良.基于分数阶滑模面控制的分数阶超混沌系统的投影同步[J].物理学报,2011,60(5):050511-050518.

[15] 刘亚林,范平志.GSM-R双向认证与端到端加密[J].铁道通信信号,2005,41(4):32-34.

[16] 杨义先,钮心析.无线通信安全技术[M].北京:邮电大学出版社,2005.

[17] ERTMS.ETCS Specification-Class 1 Subset-098:RBC-RBC Safe Communication Interface V3.0.0[S].2012.

ACHAOTICENCRYPTIONMETHODFORIMPROVINGRAILWAYSAFETYCOMMUNICATION

Jiang Fengling1Tan Wen2

1(HunanVocationalCollegeofRailwayTechnology,Zhuzhou412006,Hunan,China)2(CollegeofInformationandElectricalEngineering,HunanUniversityofScienceandTechnology,Xiangtan411201,Hunan,China)

The railway safety communication protocol RSSP has a important role in the protection of railway safety communication. However, there are security risks due to attackers’ attack, which poses a threat to the safety communication of the railway. A new chaotic encryption method to protect railway safety communication based on the unique characteristics of chaotic signals is presented. The transmitted signals were modulated to the chaotic signal with chaotic masking. In this way, the mixed signal was similar to the clutter signal, so the protected information would not be easy to crack and attack. Finally using synchronization of fractional order hyperchaotic system, the useful signals of railway communication were recovered from the mixed information for 6.2 seconds. The security and effective transmission of the information was realized, and the security and reliability of the railway communication was ensured. The consistency of the results of numerical simulation and theoretical analysis demonstrates the effectiveness of the proposed scheme.

Fractional-order hyperchaotic system Synchronization control Secure communication

2017-03-16。国家自然科学基金项目(60835004，61603132，61503134)；湖南省自然科学基金项目(14JJ3107)；教育部重点项目(211118)；湖南省科技计划项目(2015JC3111)；湖南省教育科学研究项目(15C0913)。蒋逢灵，讲师，主研领域：混沌理论，安全通信。谭文，教授。

TP391 U285

A

10.3969/j.issn.1000-386x.2017.12.033