基于伪随机阵列和正弦光栅的结构光标定

王静强 刘桂华 赵碧霞 王玉玫

(西南科技大学特殊环境机器人技术四川省重点实验室 四川 绵阳 621010)

基于伪随机阵列和正弦光栅的结构光标定

王静强 刘桂华 赵碧霞 王玉玫

(西南科技大学特殊环境机器人技术四川省重点实验室 四川 绵阳 621010)

针对投影仪-摄像机结构光系统标定精度低的问题，提出一种基于伪随机阵列与正弦光栅结合的标定算法。该方法直接对标定板角点进行编码，根据角点在不同坐标系下的点对关系求解系统参数，提高了传统的编码精度和结构光系统标定精度。在正弦光栅条纹中心处投射伪随机阵列，根据伪随机阵列窗口的唯一性和相移法可求出正弦光栅的真实相位；分别在水平和竖直方向投射正弦光栅，根据不同方向的真实相位值形成对标定板角点的唯一编码；根据编码值获得标定板角点在投影仪像平面、摄像机像平面和世界坐标系下对应点集，根据相机标定算法可得到投影仪、相机的内外参数。该方法直接对标定板角点高精度编码，求解世界坐标点和像素坐标点的对应关系，仅需要普通棋盘格标定板可实现高精度标定。实验结果表明最大反投影残差为0.7像素，棋盘格角点重建均方差为0.08 mm。

伪随机阵列 正弦光栅 投影仪标定

0 引 言

在三维测量领域，基于机器视觉的测量技术有着广泛的应用。光栅和伪随机码投影技术是主动光三维视觉主要的编码方法，具有高精度、高分辨率、非接触式等优点。在视觉引导、工业测量、逆向工程等方面有着广阔的研究前景。由单相机-投影仪组成的结构光测量系统，利用投影仪投射图形可以作为相机成像的逆过程的原理，将投影仪和相机作为两个约束，满足三角测量的必备条件。传统的系统测量需要由投影仪投射伪随机码、格雷码、正弦光栅等编码图案，摄像机采集经由物体深度信息调制的变形图案，根据图像中编码图案的变化来恢复物体的三维信息。其中系统的结构参数标定对重建结果影响很大，主要包括相机和投影仪的内参数以及外参数标定。

高治华提出的投射圆点图案的标定方法[1]，首先将圆点图案投射在圆心标定板上，根据射影变换原理建立投影仪图像和摄像机图像的对应关系。这种方法依赖于摄像机标定的精度，而且需要解出投射的圆形图案和标定板标记点的位置关系，然后才能得到圆形标志点在平板上和投影仪图像坐标，增加叠加误差造成标定精度下降。才啟胜等提出的基于神经网络的结构光标定法[2]，该方法虽然简化了建模的复杂度和提升了适应性，但得到投影仪近似模型且训练需要数据量大、耗时长。唐苏明等提出基于伪随机码标定法将伪随机码用在角点编码中[3-4]，在一定程度上改善了算法，但在求取标记点世界坐标时采用交比不变性，依然有累计误差。雷震等提出可切换棋盘格与白板的特制标定板来标定结构光系统[5]。在白板上投射网格图案，利用摄像机的标定结果求取特征点三维坐标，其系统标定精度严重依赖于摄像机标定。陆军等提出了基于格雷码和线移编码的结构光系统标定法[6]，该方法将格雷码应用于标定，减少了棋盘格背景对编码图案的影响，提高了精度，但格雷码编码与解码耗时，不利于在线实时标定。Ouellet等提出的标记圆标定法[7]，投射标记圆在标定板上，在摄像机像平面中根据摄影变换求出标记点三维坐标。该方法使用投射的标记圆在不同坐标系下的坐标点，对结构光系统标定。相比于直接利用标定板的标准圆心在不同坐标系下的坐标的方法，该方法增加了累计误差且受相机的标定精度影响较大。

本文提出了基于伪随机阵列和正弦光栅相结合的投影仪-相机标定方法。分别在水平和竖直方向向标定板投射正弦光栅[7-9]和伪随机码[10-11]。用伪随机阵列对投射在标定板上的正弦光栅条纹进行定级，水平和竖直方向的相位真实值对棋盘格角点形成唯一的编码，根据编码值实现世界坐标点和相机坐标点、投影仪坐标点的完全对应。根据张正友标定法[3]可实现对相机-投影仪的内外参数标定，本文方法直接对标准的标定板角点进行唯一编码，并使用标定板角点在不同坐标系下的对应关系标定系统参数，减少了传统方法中使用投射的标记点进行系统标定时所造成的累积误差且不依赖于摄像机的标定结果。

1 系统方案

系统的总体方案设计如图1所示。首先控制投影仪和相机，当投影仪在水平和竖直方向向标定板投射初始相位为0、π/2、π，3π/2的正弦光栅时，双目相机采集不同相位的图片。然后投射伪随机码阵列，用同样的方式记录标定板上的图案。

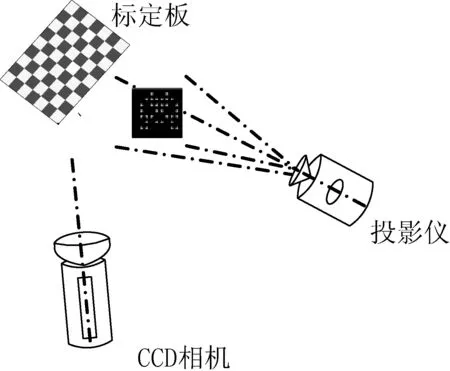
图1 系统平台设计

系统流程如图2所示。根据相机拍摄的水平和竖直方向正弦光栅和伪随机码，可以解得两个方向的真实相位值，提取棋盘格的角点。根据角点的像素坐标和水平与竖直方向的相位真实值，实现对棋盘格角点的唯一编码。在投影仪投射的图案中，每个像素都有其唯一的编码，利用编码值可以求出标定板角点在投影仪坐标系、世界坐标系、相机坐标系下的坐标。根据张正友标定法求出相机和投影仪的内参数及投影仪和相机之间旋转平移矩阵。

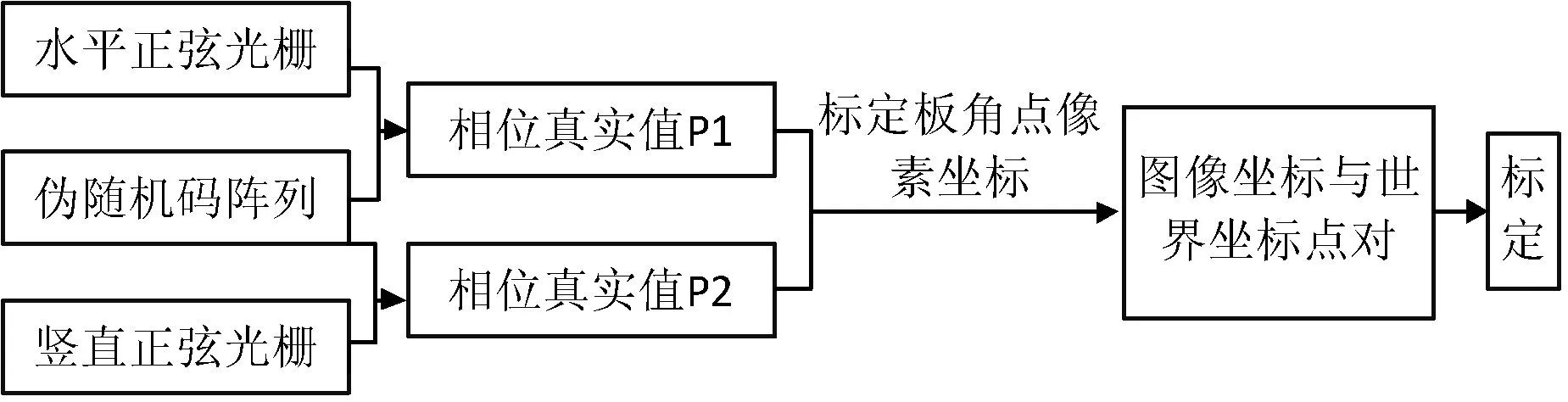
图2 系统流程图

2 算法设计

2.1 伪随机阵列应用

2.1.1 伪随机码生成

伪随机序列由本原多项式式(1)指定的移位寄存器产生。

H(x)=xm+km-1xm-1+…+k2x2+k1x+k0

(1)

选取的移位寄存器有四种状态，且令本原多项式系数GF(q)={0,1,w,w2}，w为本原。移位寄存器可以输出一个周期为T的伪随机序列。

T=qm-1

(2)

式中：m为寄存器个数，q为存储器状态数。伪随机序列输出时需要不断地更新最左边移位寄存器的值pa+m。

pa+m=h(pa+m-1,pa+m-2,…,pa)

(3)

本文选取存储器的状态为0和1。构建的伪随机序列周期为64，伪随机阵列为7行9列。阵列特性窗口为3行2列，m=6。故本原多项式为h(x)=x6+x+1，反馈移位寄存器如图3所示。

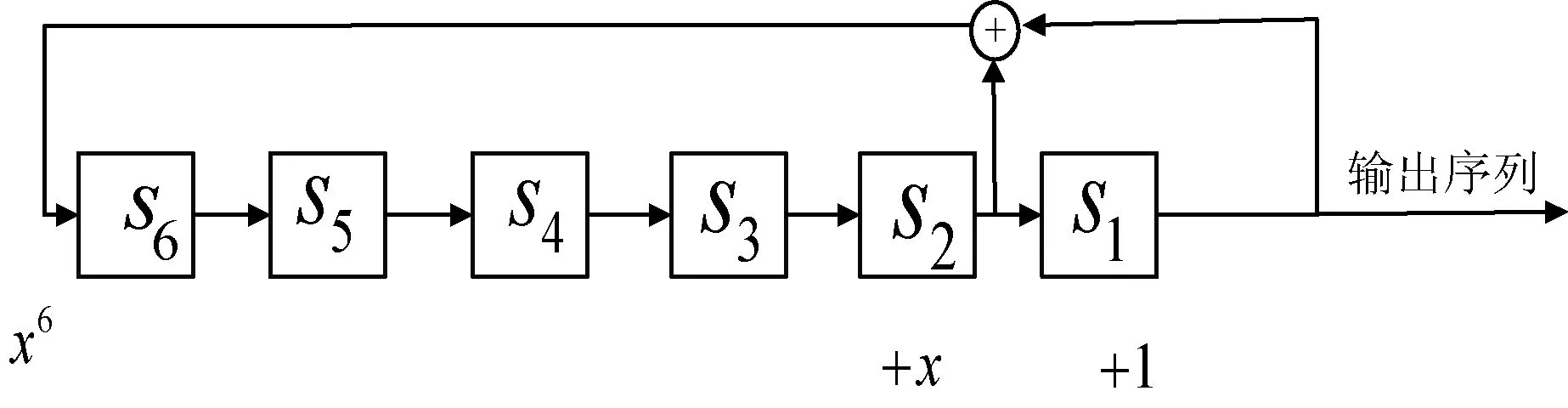
图3 移位寄存器图

式中：⊕表示摸2加法。设序列初始值为000001，则生成周期为63的伪随机序列为：

00000100001100010100111101000111001001011011101

1001101010111111。

2.1.2 伪随机阵列编码

伪随机阵列在指定的窗口大小下具有唯一特性，假设构成伪随机阵列为A，

(4)

根据式(4)得到的周期为7行9列的伪随机阵列如图4(a)所示。将该阵列应用在标记圆编码中，得到如图4(b)所示伪随机编码圆。

图4 伪随机编码圆图

2.2 正弦光栅相位解包裹

正弦光栅的解码包括相位主值的求取和真实相位值的展开两步[12-13]。在本文采用四步相移法计算包裹相位。由于正弦光栅投射到漫反射物体表面后，CMOS相机获取的变形栅图像满足公式：

F0(x,y)=A(x,y){B(x,y)+C(x,y)cosφ(x,y)}

(5)

式中：A(x,y)表示物体表面的反射率、B(x,y)为背景光强，C(x,y)为条纹幅度，φ(x,y)是初始相位。

根据式(5)可以得出：

(6)

(7)

从式(3)、式(4)中可以计算出n帧相移的相位函数[7]：

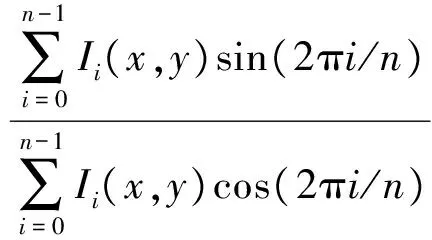
(8)

本文选择四步相移法，故n=4，根据式(5)解得相位主值为：

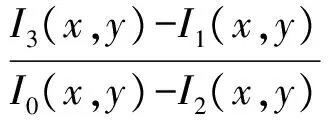
(9)

2.3 正弦光栅相位真实值求取

根据式(9)得到的正弦光栅的相位主值在[-π,π]，需要求出真实的相位值才能用于棋盘格角点编码。本文利用伪随机阵列窗口的唯一特性对正弦光栅条纹进行定级，首先将本原为0和1的伪随机阵列用红色和绿色圆表示。如图4所示，编码图案的圆心与正弦光栅的条纹中心一一对应，编码圆和正弦光栅分别投射于标定板上，根据透视投影原理，圆心在同一直线上的编码圆在标定板上的像仍然共线。如图4所示，3行2列的窗口中，左上角第一个圆心定义为a11，从a11到a1n定义为1级，从am1到amn定义为m级。则条纹级数q由式(10)求出:

(10)

式中：a为在标定板上提取到的编码圆阵列中子窗口为3行2列的编码值。

由摄像机拍摄标定板上的编码圆图案，提取圆心并根据圆心的窗口特性确定圆心所在的级数。将编码相同的圆心拟合为直线，该直线在平面标定板上与正弦光栅的条纹中心线重合，因此每条直线的级数代表正弦光栅的条纹级数。

由式(9)得到正弦光栅的相位主值φ，由式(10)求出正弦光栅条纹级数q，将φ和q代入式(11)可以得到相位真实值φ。

φ=φ+2qπ

(11)

2.4 标定板角点编码与对应点匹配

由于采用水平和竖直方向的光栅投射于棋盘格标定板上，对于棋盘格的每个角点Ci，在水平方向上正弦光栅相位真实值为ph，在竖直方向上正弦光栅相位真实值为pv，在水平和竖直方向上ph和pv的值是唯一的，因此世界坐标系下任意角点Ci的编码值设为(pv,ph)，如图5所示。

图5 角点编码图

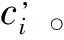
2.5 结构光系统坐标标定

摄像机模型视为理想的小孔成像模型如图6所示。

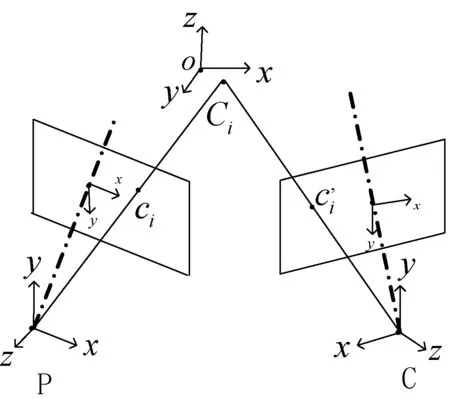
图6 投影仪模型图

根据透视投影原理可得到任意空间点在像平面的对应关系：

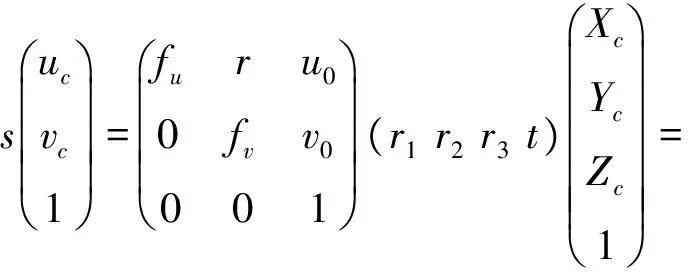
(12)

靶标平面的角点Ci与投影仪像平面对应点ci之间的变换关系为：

sci=(h1h2h3)Ci=HCi

(13)

将点集Si(Ci，ci)代入目标函数：

(14)

可求得H，H求出后由旋转矩阵的正交性可得：

(15)

求出A后，每一次标定的外参数为：

(16)

将世界坐标系下棋盘格角点Ci重投影到投影仪像平面构建目标函数：

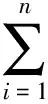
(17)

最小化目标函数求得在投影仪的内参数和在投影仪坐标系下的外参数。同理，根据点集Si(Ci，ci)可求得相机的内参数A′,外参数R′、T′。设相机坐标系为全局坐标系，需要将投影仪坐标系变换到像机坐标系下，则投影仪透视矩阵为：

H=A[RT]-1R′T′

(18)

根据三角测量原理,空间中任意一点Ci的三维坐标可由式(10)计算得到：

(19)

式中：H为摄像机透视矩阵，H′为相机透视矩阵。

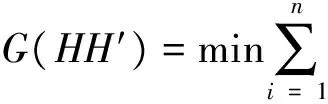
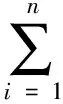
(20)

式中：M为式(10)得出的三角测量方程；P为透视投影方程。最小化目标函数可得投影仪-相机模型的结构参数。

3 实验结果及分析

实验平台如图6所示，采用Inter i7730处理器，三菱MD-565X投影仪分辨率为1 280×1 024，BASLER PIA 2400工业相机，分辨率为1 280×1 024。

图7 实验平台图

首先水平和竖直方向的正弦光栅以及伪随机码投射于标定板上，为了减小棋盘格角点对编码造成影响，用一层薄纸覆盖在标定板表面，如图8所示。

图8 光栅和伪随机码投影图

分别在水平和竖直方向上利用四步相移法，求出标定板上正弦光栅的相位主值，将伪随机编码圆进行圆心提取并确定圆心编码值。根据伪随机阵列3行2列的窗口特性，由式(10)可以确定每个圆心的所在正弦光栅的条纹等级。将条纹等级相同的圆心拟合为直线，将条纹级数直线与正弦光栅相位主值结合解得两个方向的相位主值，如图8中所示。

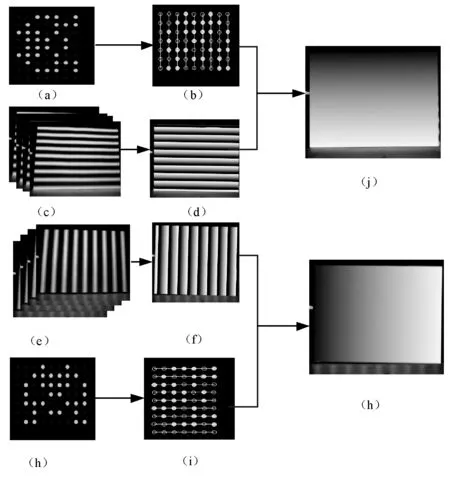
图9 相位真实值图

图9(a)为水平方向伪随机码，(b)中伪随机码拟合直线代表正弦光栅条纹级数，(c)为四幅相位初始值相差π/2的正弦光栅，(d)为求得的相位主值，(j)、(h)为根据相位主值和条纹级数解得的水平和竖直方向的正弦光栅相位真实值。

根据水平和竖直方向的相位真实值对棋盘格的角点进行编码，如图10所示。

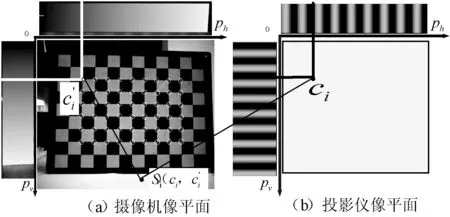
图10 角点解码对照图

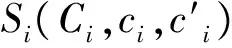
表1 投影仪-相机参数

为了验证标定精度，将世界坐标系下棋盘格角点反投影到投影仪像平面，如图11所示，得到反投影均方差为0.7个像素。

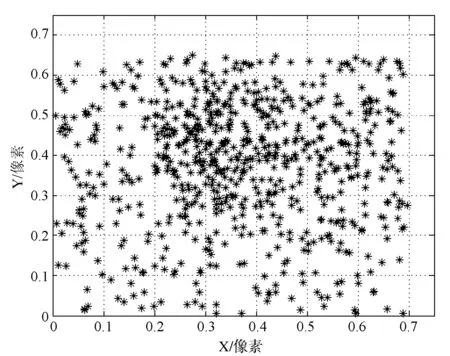
图11 投影仪反投影残差图

将棋盘格角点进行三维重建，得到的角点之间的距离与真实角点之间的距离的做差，根据不同的标定步数，得到均方误差分布，如图12所示。

图12 重建角点误差图

由图11知，8步时可以达到最优标定。基于标记圆的标定方法需要在摄像机平面中，求出投射的圆形图案和标定板标志点的位置关系，根据射影定理得到图案在不同坐标系下的坐标。摄像机的精度对系统影响较大。格雷码标定法采用交比不变性求解投射的格雷码标志点，采用间接的数据对系统进行标定，造成累计误差较大。本文方法直接对棋盘格角点进行编码，根据编码值直接寻找角点在不同坐标系下对应点集，计算系统的结构参数，直接用标定板标准角点点集对系统进行标定，消除了使用间接数据造成的误差且不依赖于摄像机标定精度。本文方法与基于标记圆的标定法和格雷码标定法作对比，本文算法精度可以达到0.08 mm，精度明显高于标记圆标定法和格雷码标定法。

4 结 语

针对传统投影仪-相机结构光系统标定精度低的问题，本文提出了基于伪随机阵列和正弦光栅相结合的方法。该方法不依赖于相机标定，直接对棋盘格角点进行编码，不同于传统标定法中根据交比不变性得到的不同坐标系下的角点坐标。直接得到用于标定的角点坐标，使反投影均方差减小到0.7个像素，角点重建最大均方误差为0.08 mm，提高了标定精度。

[1] 高治华, 王昭, 黄军辉,等. 基于射影变换的结构光测量系统中投影仪标定方法[J]. 中国激光, 2012, 39(10):154-161.

[2] 才啟胜, 相里斌, 方煜,等. 基于神经网络的结构光系统标定[J]. 光子学报, 2016, 45(5):81-86.

[3] Zhang Z. Flexible Camera Calibration by Viewing a Plane from Unknown Orientations[C]//The Proceedings of the Seventh IEEE International Conference on Computer Vision. IEEE, 2002:666-673.

[4] 唐苏明, 张旭, 屠大维. 伪随机编码结构光系统的标定[J]. 仪器仪表学报, 2014, 35(6):1354-1362.

[5] 雷震, 刘晓军, 卢文龙,等. 一种结构光测量技术中的投影仪标定方法[C]//全国光学测试学术交流会,2014.

[6] 陆军, 宋成业. 基于格雷码和线移编码的结构光系统标定[J]. 光电子·激光, 2012(6):1146-1151.

[7] Quellet J N, Rochette F, Hebert P. Geometric calibration of a structured light system using circular control points[C]//The Fourth International Symposium on 3D Data Processing, Visualization, and Transmission, 2008 June 18-20. Atlanta: IEEE Computer Society, 2008:16-18.

[8] 范国鹏, 周莉, 殷明,等. 基于时空转换法的正弦波光栅尺位移测量系统设计[J]. 传感技术学报, 2015, 28(9):1367-1372.

[9] 昌驰, 朱革, 付敏,等. 基于光场耦合的时栅位移传感器设计[J]. 传感器与微系统, 2016, 35(2):113-115.

[10] Dong Z, Hu N. A method for the detection of long pseudo-random code DSSS signals based on the processing of delay-multiply (II)-the estimation of the information symbol period and the pseudo-random code sequence[C]//IEEE International Conference on Communication Technology. IEEE, 2008:233-236.

[11] Zhang S N, Zhao H C, Bing W U. LFM Interference Excision Technique in Pseudo-random Code Fuse Based on Fractional Fourier Transform[J]. Acta Armamentarii, 2006, 27(1):32-36.

[12] 尚忠义, 李伟仙, 董明利,等. 基于四步相移光栅投影的三维形貌测量系统[J]. 应用光学, 2015, 36(4):584-589.

[13] 戴美玲, 杨福俊, 何小元. 基于双频彩色光栅投影测量不连续物体三维形貌[J]. 光学精密工程, 2013, 21(1):7-12.

CALIBRATIONOFSTRUCTUREDLIGHTBASEDONPSEUDORANDOMARRAYANDSINEGRATING

Wang Jingqiang Liu Guihua Zhao Bixia Wang Yumei

(SpecialEnvironmentRoboticsLaboratoryofSichuanProvince,SouthwestUniversityofScienceandTechnology，Mianyang621010，Sichuan，China)

Aiming at the low calibration accuracy of projector and camera structured light system, a calibration algorithm based on pseudorandom array and sine grating is proposed. This method directly encodes the corners of the calibration plate and solves the parameters of the system by the relationship between points in different coordinate systems. It improves the traditional coding precision and the calibration precision of structured light system. First, the pseudorandom array was projected at the center of the sine grating fringe, and the true phase of the sine grating was obtained according to the uniqueness of the pseudorandom array window and phase-shifting method. Secondly, sine grating was projected in horizontal and vertical directions respectively. Each corner of the calibration plate would have a unique code according to the true phase value of different direction. Lastly, the corresponding points in camera and projector as well as world coordinate system was obtained by the code value of corners. The projector and camera’s internal parameters as well as external parameters was figured out according to the corresponding points.This method encodes the corners of the calibration plate to solve the correspondence between the world coordinates points and the pixel coordinates point directly. It only needs common checkerboard calibrated plate can realize high precision calibration. The experimental results show the maximum back projection error is 0.7 pixels and the mean square deviation of corners is 0.08 mm.

Pseudorandom array Sine grating Projector calibration

2017-06-04。国家核能开发科研项目([2016]1295)；校创新团队建设基金项目(14TDTK01)。王静强，硕士生，主研领域：图像处理及计算机视觉。刘桂华，教授。赵碧霞，硕士生。王玉玫，硕士生。

TP391

A

10.3969/j.issn.1000-386x.2017.12.022