基于集合经验模态分解和灰色神经网络的船舶交通流预测*

肖进丽 刘明俊 李晓磊

(武汉理工大学航运学院1) 武汉 430063) (湖北省内河航运技术重点实验室2) 武汉 430063)

基于集合经验模态分解和灰色神经网络的船舶交通流预测*

肖进丽1,2)刘明俊1,2)李晓磊1,2)

(武汉理工大学航运学院1)武汉 430063) (湖北省内河航运技术重点实验室2)武汉 430063)

为提高船舶交通流预测精度，更科学地为海事监管、港口水域规划布局提供参考，结合灰色神经网络模型(grey neural network, GNN)和集合经验模态分解(ensemble empirical mode decomposition, EEMD)对船舶交通流建立了EEMD-GNN组合预测模型，并基于Matlab软件，以2007年1月—2015年12月荆州长江公路大桥断面船舶交通流月流量统计数据为样本进行了实例分析.首先对船舶月流量时间序列样本数据进行EEMD分解以降低序列的非平稳性，然后对EEMD分解后获得的各分量建立GNN模型进行预测，并将各分量预测值进行叠加即得到EEMD-GNN模型的预测结果.最后，将EEMD-GNN模型预测结果与传统GNN模型进行对比分析.对比分析结果表明，EEMD-GNN模型较传统GNN模型的预测精度更高，能更好地反映船舶月交通流量的变化情况.

船舶交通流；集合经验模态分解；灰色神经网络；组合预测

0 引 言

近年来，随着我国水上交通运输业的快速发展，船舶交通流量日益增长，与通航安全、通航效率，以及通航资源之间的矛盾也日益突显.为缓解这一矛盾，更好地保障水域通航安全、提高水域通航效率、科学合理规划水域布局，有必要通过对船舶交通流进行预测和研究来把握其未来的发展趋势，为海事监管、港口规划和设计等方面提供科学参考[1]

目前，国内外有关船舶交通流预测的研究众多，并且主要采用了基于模型的定量分析方法，如时间序列分析、小波分析、人工神经网络、支持向量机等，均取得了较好的预测效果[2-5].人工神经网络作为一种数据驱动算法，可以映射出时间序列间复杂的非线性关系，具有很强的非线性信息处理能力，在预测领域应用较为成熟.由于传统人工神经网络采用梯度下降的学习方法，易陷入局部极小、引起振荡以及收敛速度慢等固有缺陷，实用性不强[6].灰色神经网络兼具了灰色模型少数据建模和人工神经网络自学习、非线性映射的优点，与传统人工神经网络相比，其网络的泛化能力和学习速度都有所提高，故近年来在预测领域逐渐得以应用[7].但是，船舶交通流序列是一种具有非线性和非平稳性的特殊时间序列，灰色神经网络虽可以很好地拟合船舶交通流序列的非线性部分，但是其非平稳的部分会对预测效果造成较大影响，因而降低船舶交通流序列的非平稳性对于提高预测的精度十分重要.集合经验模态分解是一种改进的经验模态分解(empirical mode decomposition,EMD)方法，可以将一个复杂的非线性、非平稳性时间序列自适应分解为一系列尺度不同的线性、平稳信号，从而极大降低时间序列的非平稳性[8].

针对船舶交通流序列的非线性和非平稳性特性，文中提出一种将灰色神经网络模型和集合经验模态分解相结合的新型船舶交通流组合预测模型，并应用此模型对荆州长江公路大桥断面船舶交通流进行了预测和对比分析，结果表明此模型能够较好地提高预测的精度.

1 船舶交通流的非平稳性分析

船舶交通流是一种典型的时间序列，具有很明显的非线性和非平稳的特征.以长江下游某航道断面流量为例，2014年该断面的船舶月日均流量与当年元月份日流量分布见图1.

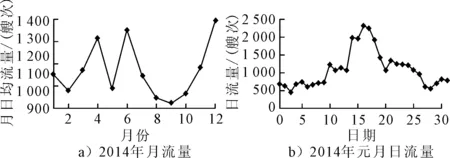
图1 长江某航道断面流量分布

图1很直观就反映出了船舶交通流的非线性特征，但其非平稳性则需要采取一定的方法进行检验.ADF检验(augmented dickey-fuller test statistic)是一种常用的时间序列平稳性检验方法，它通过检验序列中是否存在平方根来判断序列是否平稳，如果不存在单位根则序列是平稳的，如果存在单位根则序列是不平稳的，因此，为分析以上这两组数据(月日均流量和日流量)的非平稳性，可基于EViews软件对其进行ADF检验，检验结果见表1.

表1 船舶序列的ADF检验

由表1可知，两组数据的t统计值的绝对值均大于其显著性水平为1%，5%，10%的临界值，接受存在一个单位根的假设，表明这两组数据均为非平稳时间序列.

2 GNN预测模型

2.1 灰色GM(1，1)模型

GM(1，1) 首先对原始时间序列做一次累加，然后利用累加后的数据建立微分方程形式的动态模型.设原始时间序列为

x(0)={x(0)(1),x(0)(2),…，x(0)(n)}

(1)

对x(0)做一次累加生成序列

x(1)={x(1)(1),x(1)(2),…，x(1)(n)}

(2)

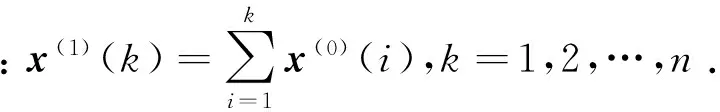
根据新时间序列x(1)，建立微分方程为

(3)

该方程的解为

k=0,1,…,n

(4)

1.2 嵌入型GNN模型

基于嵌入型结构，采用BP神经网络与灰色预测模型组合构成嵌入型灰色神经网络预测模型[9]，具体建模过程为：

1) 确定船舶交通流数据的时间序列长度N，生成初始时间序列x(0).

2) 将初始时间序列x(0)按式(2)进行一次累加生成新序列x(1).

3) 建立三层BP神经网络，包括输入层、隐含层和输出层.将序列x(1)作为BP神经网络的输入向量，设置训练参数对BP神经网络进行训练，直至样本集总误差达到所要求精度为止，此时输出向量数据为y(1).

4) 对输出向量y(1)按式(3)做一次累减还原处理，最终得到船舶交通流预测值.

k=0,1,…,n

(5)

3 EEMD-GNN组合预测模型

3.1 EEMD算法

EEMD(ensemble empirical mode decomposition)为EMD的改进方法，EMD则是Sreedevi等[10]提出的一种有效处理非线性和非平稳信号的自适应分解算法.EMD的基本思想是根据信号本身在时间尺度上的局部特性，通过筛分过程(shifting process)自适应地将信号分解为有限个反映时序信号内在特征的“固有模态分量(intrinsic mode function, IMF)”，从而对信号完成平稳化处理.但是应用研究又发现，当待处理的信号中存在异常干扰信号时，EMD会存在模式混叠问题.针对这一问题，基于白噪声中均匀分布的各种频率成分能被规律性分离开来的现象，Wu等[11]提出一种在待分解待信号中加入白噪声，使不同尺度的信号自动映射到合适的参考尺度上，从而克服EMD模态混叠缺陷、达到更好分解结果的方法，即为EEMD算法.EEMD分解主要步骤为：

1) 在待分解信号x(t)中加入白噪声n(t)获得加噪声后的总体信号X(t):

X(t)=x(t)+n(t)

(6)

2) 对总体信号X(t)进行EMD分解，得到一组IMF分量cj(t)(j=1,2…m)和一个残余分量rm(t)：

(7)

3) 给待分解信号x(t)加入不同白噪声信号ni(t)(i=1,2…N)，重复以上两步N次，分解后得到不同的IMF分量和残余分量，即

(8)

4)为消除多次添加白噪声信号对实际IMF的干扰，对各分量进行整体平均计算，获得时序信号的EEMD分解结果为

(9)

3.2 EEMD-GNN组合预测模型构建

根据以上EEMD和GNN模型，将船舶交通流在各个时间段上的观测值作为一时间序列X(t)，对序列X(t)进行EEMD分解，得到m个固有模态分量IMF和1个残差项Rm，即

X(t)=IMF1+IMF2+…+IMFm+Rm(10)

针对各个IMF和R，分别建立各自的GNN预测模型进行预测，得到各分量的预测值YIMF1，YIMF2…YIMFn和YB，最后将各分量预测值进行叠加得到船舶交通流的预测结果为

Y=YIMF1+YIMF2+…+YIMFn+YRm

(11)

综上所述，建立EEMD-GNN船舶交通流预测模型的步骤见图2.

图2 EEMD-GNN组合预测流程

4 实证研究

4.1 性能评判指标

为综合评定预测结果的性能，文中以平均绝对误差εm、均方根误差RMS作为评判模型性能的指标，为

(12)

(13)

4.2 实例分析

为验证EEMD-GNN算法的有效性，文中以荆州长江公路大桥断面2007年1月—2016年3月共111个月的船舶月流量统计数据(月均当量船舶艘次)为例进行实例分析，其统计数据时间序列见图3.

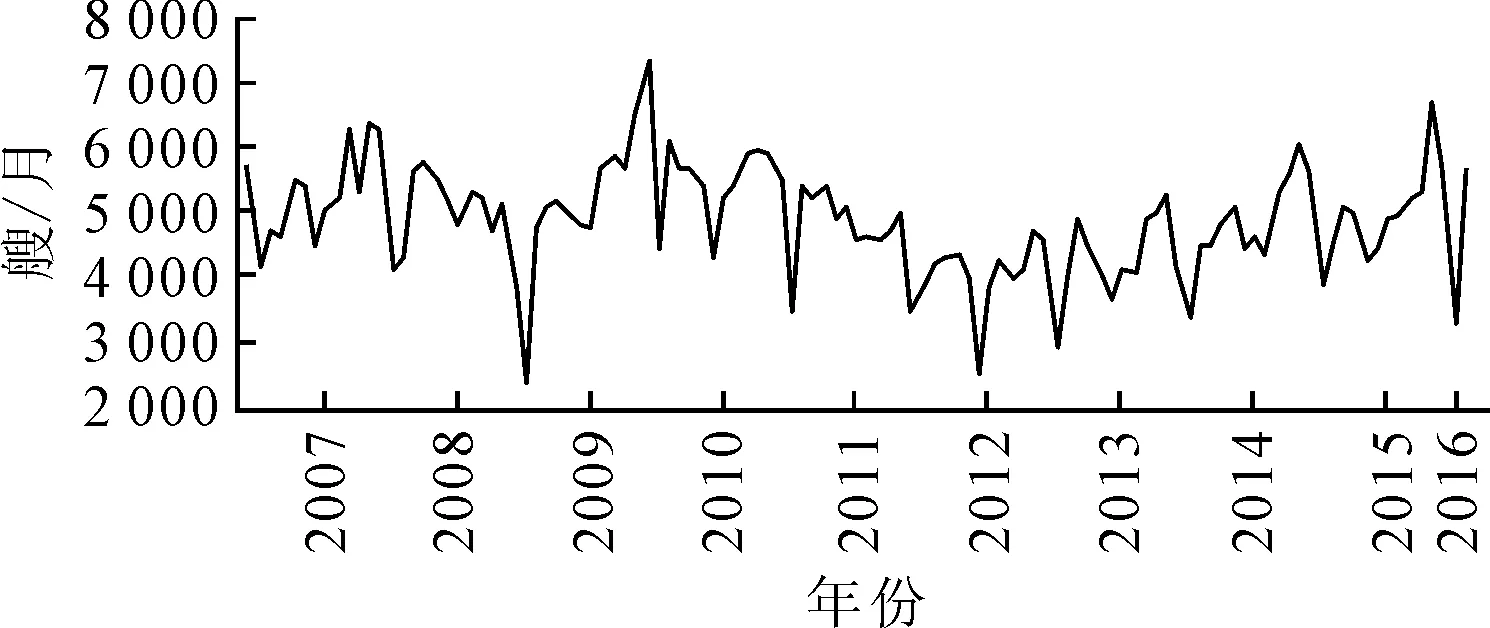
图3 某航道断面月交通流时间序列

首先对船舶月流量序列进行EEMD分解，分解结果见图4.

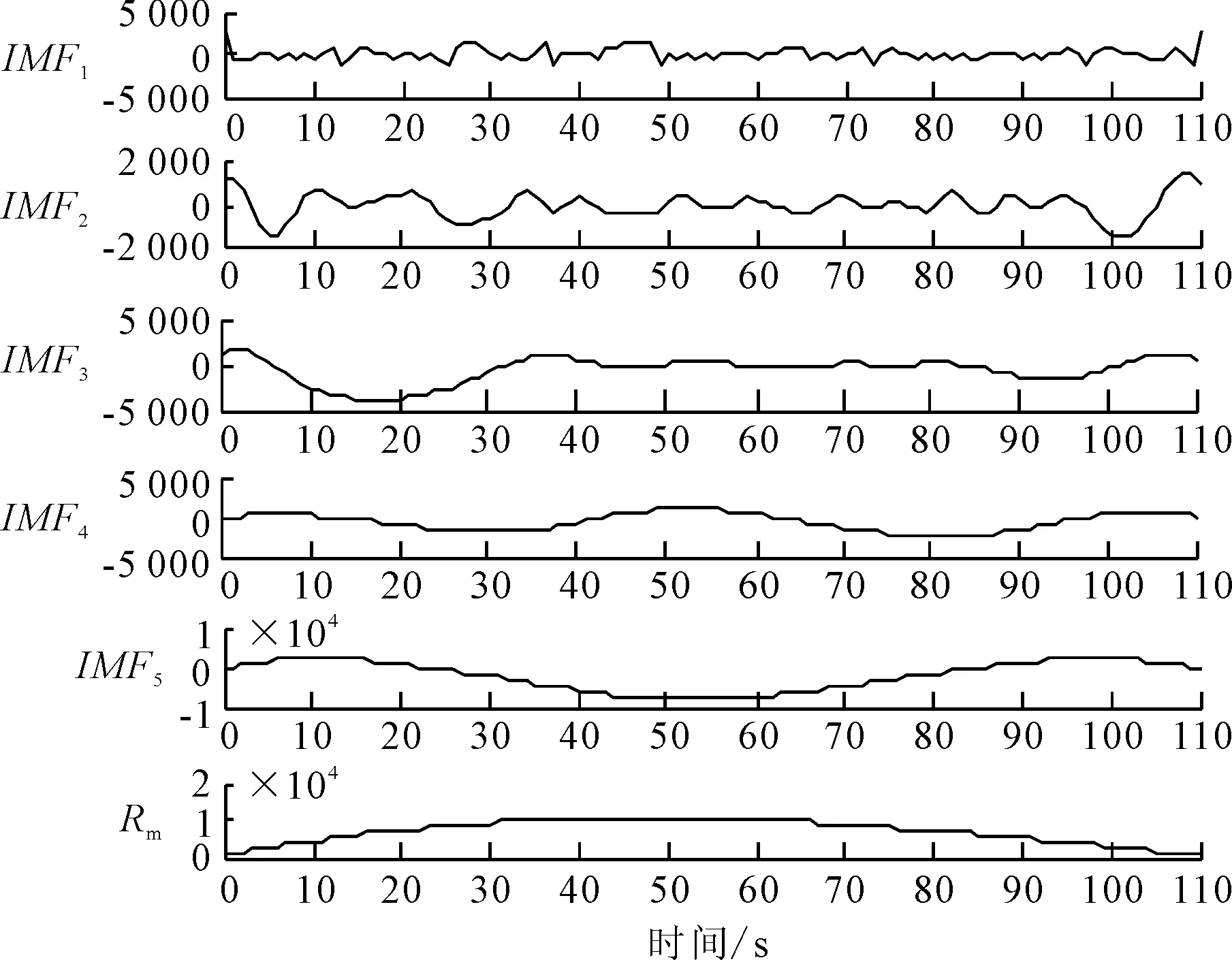
图4 EEMD分解结果

由图4可知，EEMD将船舶交通流时间序列分解为五个频率逐级降低的IMF分量和一个残差项.五个IMF分量反映出不同影响因素在不同尺度对船舶交通流时序数据的影响. 其中分量IMF1周期性波动特点不明显，反映的是外部随机因素对船舶交通流的影响；分量IMF2～IMF4的周期性波动特点较为明显，但其波动周期不均匀，反映的是通航水位变化、气候条件等外部非随机因素对船舶交通流的共同作用.残差项Rm则反映出船舶交通流时间序列长期的变化趋势.

由于经EEMD分解后的IMF和残差分量的数据个数均为111个，选取前1～99个数据作为GNN的训练样本，剩余的12个数据(12个月)作为测试样本.分别使用GNN对分解所得的各IMF分量和残差进行训练和预测， 并对各分量的预测结果叠加得到船舶交通流预测结果，并与基于GNN模型的船舶交通流预测结果和实际值进行对比，见图5.

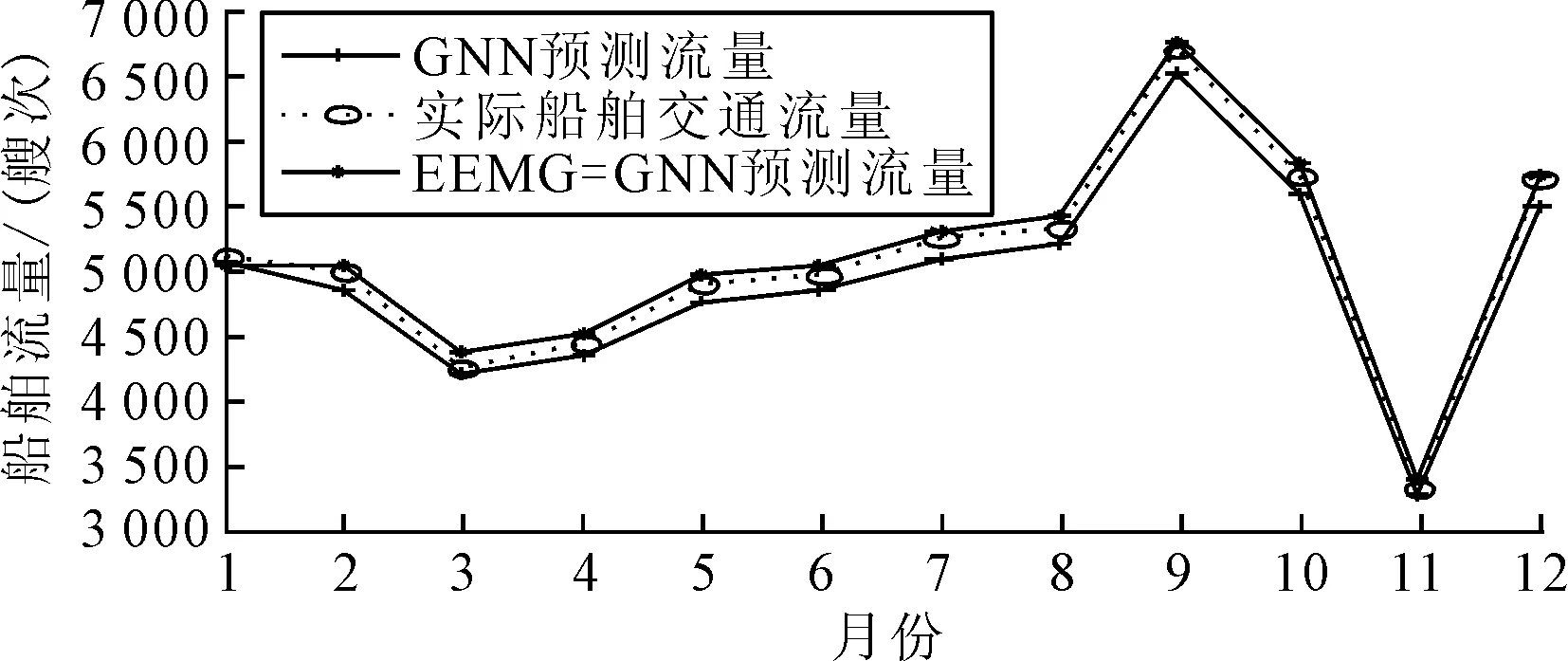
图5 EEMD-GNN及GNN的船舶月交通流预测结果

表2为两种模型基于平均绝对误差εm和均方根误差RMS的预测性能对比.

表2 EEMD-GNN及GNN预测模型精度对比

由图5可知， EEMD-GNN组合预测模型可以有效地对船舶交通流进行跟踪预测，有较高的跟踪预测效果.而表2则进一步表明，EEMD-GNN模型的预测精度优于传统GNN模型，其预测结果比传统GNN模型整体更接近于实际值.

5 结 束 语

对于船舶交通流预测，船舶交通流序列的非平稳性和非线性加大了其难度.基于EEMD可以有效分析非平稳序列的特性和GNN具有较好的非线性拟合能力，文中提出一种基于EEMD-GNN模型的船舶交通流组合预测方法.实例分析表明，与传统GNN模型相比，EEMD-GNN模型在船舶交通流预测方面具有更高的精度，在船舶交通流预测领域具有一定的实用价值.但是，由于该模型在使用EEMD对船舶流进行分解时没有考虑船舶流时间序列的端点效应问题，具有一定的局限性，需进一步研究.

[1] 金兴赋,付玉慧,张连东.基于AIS数据的成山头水域船舶交通流研究[J].大连海事大学学报,2012,38(1):33-36.

[2] ZENG D H, XU J M, GU J W, et al. Short term traffic flow prediction using hybrid ARIMA and ANN models[C]. Proceedings of the 2008 Workshop on Power Electronics and Intelligent Transportation System,2008.

[3] ANDRIUS D. Neural network approach to predict marine traffic[J]. Baltic J Modern Computing,2016(3):483-495.

[4] LIU C X, LU B C, WANG J F. Traffic flow prediction based on wavelet analysis, improved genetic algorithm, and bp neural network[C]. The 12thCOTA International Conference of Transportation Professionals, Beijing, China,2012.

[5] ZHANG H, XIAO Y J. GA-support vector regression based ship traffic flow prediction[J]. International Journal of Control and Automation,2016(2):219-228.

[6] LIU C X, SHUA T , CHEN S, et al. An improved grey neural network model for predicting transportation disruptions[J]. Expert Systems with Applications,2016(2):331-340.

[7] PAN Y Y, SHI Y D. Short-term traffic forecasting based on grey neural network with particle swarm optimization[C]. Proceedings of the World Congress on Engineering and Computer Science, San Francisco, USA,2016.

[8] 徐龙琴,李乾川,刘双印,等.基于集合经验模态分解和人工蜂群算法的工厂化养殖pH值预测[J].农业工程学报,2016,32(3):202-209.

[9] 陈淑燕,王炜.交通量的灰色神经网络预测方法[J].东南大学学报,2004,34(4):541-544.

[10] SREEDEVI G, SREENIVASULU R. Enhanced signal denoising performance by EMD-based techniques[J]. International Journal of Engineering Research and Applications,2012(6):1705-1711.

[11] WU Z H, HUANG N. Ensemble empirical mode decomposition: a noise-assisted data analysis method[J]. Advances in Adaptive Data Analysis,2009(1):36-41.

Vessel Traffic Flow Prediction Based on Ensemble Empirical Mode Decomposition and Grey Neural Network

XIAOJinli1,2)LIUMingjun1,2)LIXiaolei1,2)

(SchoolofNavigation,WuhanUniversityofTechnology,Wuhan430063,China)1)(HubeiKeyLaboratoryofInlandShippingTechnology,Wuhan430063,China)2)

To improve the predictive accuracy of vessel traffic flow and provide more reasonable decision-making basis for maritime management, port planning and development, the combination forecast model (EEMD-GNN) for vessel traffic flow is estimated based on Grey Neural Network (GNN) model and Ensemble Empirical Mode Decomposition (EEMD) method. With Matlab software, the example analysis is conducted based on the statistical data of the monthly flow of vessel traffic in Jingzhou Yangtze river highway bridge during January 2007-December 2015. Firstly, in order to reduce the non-stationary of vessel traffic flow time series, the sample data is decomposed by the EEMD method and a set of decomposed components are obtained to predict the results by GNN model. Afterwards, the predictive results of all components are added together to form the final results: the EEMD-GNN model. Finally, the prediction results of EEMD-GNN model are compared with those of the traditional GNN model. The results show that the EEMD-GNN model has higher prediction accuracy compared with traditional GNN model, which reflects the future trend of monthly vessel traffic flow more accurately.

vessel traffic flow; EEMD; GNN model; combination prediction

U491.2

10.3963/j.issn.2095-3844.2017.06.010

2017-10-19

肖进丽(1976—)：女，博士，副教授，主要研究领域为交通信息处理及交通安全保障技术

*湖北省自然科学基金面上项目资助(2015CFB282)