大跨度钢桁架拱桥施工误差敏感性分析*

康俊涛 胡 杰 董培东 邢英兴曹宏猷 孙雪平 秦世强 邵光强

(武汉理工大学土木工程与建筑学院1) 武汉 430070) (中交武汉港湾工程设计研究院有限公司2) 武汉 430000)

大跨度钢桁架拱桥施工误差敏感性分析*

康俊涛1)胡 杰1)董培东1)邢英兴2)曹宏猷1)孙雪平1)秦世强1)邵光强1)

(武汉理工大学土木工程与建筑学院1)武汉 430070) (中交武汉港湾工程设计研究院有限公司2)武汉 430000)

为研究大跨度钢桁架拱桥的拱肋线形对施工误差的敏感性，以苏岭山大桥主桥为例，以设计理想状态的有限元模型为基准，研究了结构自重、刚度、温度、节段角度误差对拱肋最大悬臂状态、合龙状态、成桥状态的拱肋线形的影响.结果表明，这三种状态下的拱肋不同截面累积挠度均对同种类型施工误差的敏感性不同；这三种状态下的拱肋线形均对拼装角度最敏感，对结构自重和温度比较敏感，对结构刚度敏感性较低；在不同状态下，对施工误差最敏感的主要截面位置不同；并针对该类桥梁的施工特点，提出误差识别和拱肋线形控制的建议.

钢桁架拱桥；拱肋线形；施工误差；敏感性

0 引 言

钢桁架拱桥具有外形美观、跨越能力大、承载能力高、耐久性能好等优点[1]，在大跨径桥梁选型中具有较强的竞争力.

许多学者对此类问题进行了研究，郭玉龙[2]的研究表明,拱肋桁架的节点板、高强螺栓和横隔板质量占拱肋总质量的10%以上，且对施工阶段的杆件应力影响显著.由文献[3]可知，节点刚域效应对悬臂拼装的钢桁架连续梁桥施工过程中的杆件应力影响明显.魏群[4]研究了节点刚度对坝陵河大桥成桥状态构件力学特性的影响，表明节点刚度会导致钢桁架加劲梁整体刚度增大，杆件应力分布差别明显.钢桁架的加工、制作和安装温度一般存在地域差异和季节差异，所处环境温差大，且与设计基准温度差别较大.拱肋拼装角度误差对榕江特大桥拱肋线形的影响较大，线形偏差基本来源于角度误差[5].卢伟升[6]对拱肋多种典型的施工标高误差进行了结构的成桥受力影响分析，得出不同的施工标高误差类型对结构的成桥受力影响差别很大.吴海军[7]研究了钢-混凝土组合拱桥竖转施工中的合龙误差对箱形钢拱肋受力情况的影响，为同类桥梁的强迫合龙提供了理论依据.

目前，对于钢桁架拱桥施工误差的研究集中在施工过程中的结构受力情况，而对施工过程中不同状态下的拱肋线形对不同施工误差的敏感程度研究较少.文中拟以苏岭山大桥主桥设计理想状态有限元模型为基准，研究结构自重、刚度、温度和节段拼装角度误差对拱肋最大悬臂状态、拱肋合龙状态及成桥状态下的拱肋线形的影响，对比确定不同状态下的拱肋线形对不同施工误差的敏感程度.

1 工程概况及计算模型

1.1 工程概况

苏岭山大桥主桥为三跨下承式连续钢桁架拱桥，跨径组合为70 m+240 m+70 m，全长为380 m，桥面全宽为43.9 m，见图1.

图1 苏岭山大桥主桥(单位：cm)

拱肋由两片N桁架和八道空间桁架式一字风撑组成，两片拱肋桁架横向中心间距38.2 m.N桁架由上弦杆、下弦杆和腹杆组成，上、下弦杆采用高强螺栓连接的箱形截面，上弦杆采用二次抛物线和圆曲线相结合，下弦杆采用抛物线，矢高54 m，矢跨比1/4.444，中跨腹杆采用工字形截面，边跨腹杆采用1.498 m×0.8 m的箱形截面.风撑弦杆采用平行四边形箱形截面，竖腹杆、平联杆均采用H形截面.桥面主纵梁内宽1.5 m，竖向中心线处全高2.7 m.纵梁间设置钢横梁，钢横梁上翼缘设双向2%横坡，桥梁中心线处腹板高3.054 m，横梁分工字形截面和箱形截面.主墩采用直径4 m的实心圆形墩，两墩柱之间设直径3.2 m的实心方形系梁；边墩为直径2 m的四柱实心圆形墩.

苏岭山大桥主桥主要施工流程如下：①在两岸临时支撑平台上拼装边跨拱肋和边跨横梁；②安装塔架和缆索系统并悬臂拼装主跨拱肋；③张拉后锚索和前扣索并悬臂拼装剩余主跨拱肋直至拱肋合龙；④安装并张拉临时系杆，吊装主跨桥面梁节段直至主梁合龙；⑤二次张拉吊杆，调整主梁线形；⑥解除锚扣系统和临时系杆，安装桥面系及附属构件.

1.2 计算模型

采用有限元分析软件MIDAS Civil 2015建立设计理想状态有限元模型，见图2.

图2 设计理想状态有限元模型

模型中拱肋、主纵梁、横梁、扣塔采用梁单元模拟，扣索、临时系杆、吊杆采用桁架单元模拟.全桥共划分为3 736个单元，2 673个节点，各主要构件材料特性见表1.施工过程模拟按设计图纸考虑的临时荷载包括边跨临时压重、扣塔自重和扣索索力等.边跨压重、防撞栏杆、桥面铺装荷载均按均布荷载考虑.拱肋最大悬臂状态和合龙状态：中支座固定，边支座纵向活动；成桥状态：一中支座固定，其余支座纵向活动.

表1 主要构件材料特性表

2 控制指标的确定

钢桁架拱桥的线形、应力对于施工质量和结构安全至关重要，但目前应力测量精度不够，实测值波动较大，而线形测量精度较高，现场操作方便快捷.柳鑫星[8]对之江大桥线形控制技术的研究表明，对大跨度钢桥的施工进行线形控制，施工误差小，能保证成桥线形满足设计和规范要求.王虎胜[9]采用线形控制方法对某大跨度刚构桥的合龙方案进行了对比分析，为该类桥梁的合龙方案选择提供了宝贵建议.王海峰[10]的研究结果表明，在大跨度桥梁的悬臂浇筑施工中，保持主梁线形在控制范围内是确保结构受力安全的一个重要手段.因而，选取各控制截面的累积挠度作为误差敏感性分析的控制指标.

以苏岭山大桥主桥设计理想状态有限元模型为基准，分析结构自重、刚度、温度和节段拼装角度误差按不同倍数变化对拱肋最大悬臂状态、拱肋合龙状态和成桥状态的拱肋线形的影响，以便与大桥施工过程中的拱肋实测线形进行对比，对实际施工误差的类型和大小进行识别，进而为拱肋线形的调整和控制提供参考.其中，结构自重按照1.03，1.06，1.09，1.12的倍数变化，自重的调整通过改变材料的容重实现；结构刚度按1.03，1.06，1.09，1.12的倍数变化，刚度的调整通过改变材料的弹模实现；结构温度按照-20，-10，10，20 ℃变化，温度的调整通过系统升降温实现；节段拼装角度误差Δθ按照-0.002，-0.001，0.001，0.002 rad变化，角度误差的调整通过使悬拼节段绕前一节段上弦杆拼接点整体旋转相应角度实现，节段整体向上转动为正，向下转动为负.

3 施工误差敏感性分析

3.1 拱肋最大悬臂状态

结构自重、刚度、温度和拼装角度变化时，拱肋最大悬臂状态下的拱肋各控制截面累积挠度与设计理想状态的比较结果见图3.图中正值挠度表示拱肋上抬，负值挠度表示拱肋下挠.

图3 四种因素对最大悬臂状态主拱线形的影响

由图3可知：①随着结构自重的增大，拱脚处截面下挠4%～17%，(1/8)L处截面下挠23%～91%，(1/4)L处截面下挠23%～93%，(3/8)L处截面下挠26%～102%.②随着结构刚度的增大，拱脚处截面上抬3%～10%，(1/8)L处截面下挠6%～23%，(1/4)L处截面下挠7%～24%，(3/8)L处截面下挠7%～25%.③随着结构温度的变化，拱脚处截面累积挠度变化3%～6%，(1/8)L处截面累积挠度变化40%～81%，(1/4)L处截面累积挠度变化23%～45%，(3/8)L处截面累积挠度变化18%～35%.④随着拼装角度的变化，拱脚处截面累积挠度变化8.10～16.19倍，(1/8)L处截面累积挠度变化4.68～9.36倍，(1/4)L处截面累积挠度变化2.29～4.58倍，(3/8)L处截面累积挠度变化1.59～3.18倍.

由上述控制截面挠度变化可得：

1) 拱肋最大悬臂状态下的拱肋线形对不同类型施工误差的敏感性差别很大.其中，拱肋线形对拼装角度最敏感，累积挠度变化最大为16.19倍；对结构自重很敏感，累积挠度变化最大为102%；对结构温度比较敏感，累积挠度变化最大为81%；对结构刚度的敏感性较低，累积挠度变化最大为25%.

2) 拱肋最大悬臂状态下的拱肋不同截面累积挠度对同种类型施工误差的敏感性不同.结构自重增大，各控制截面累积挠度变化最大值为17%～102%；结构刚度增大，各控制截面累积挠度变化最大值为10%～25%；结构温度变化，各控制截面累积挠度变化最大值为6%和81%之间；拼装角度变化，各控制截面累积挠度变化最大值为3.18～16.19倍.

3) 在拱肋最大悬臂状态下，对不同类型施工误差最敏感的截面位置主要为(3/8)L处.结构自重增大，累积挠度变化最大的截面为(3/8)L处截面；结构刚度增大，累积挠度变化最大的截面为(3/8)L处截面；结构温度变化，累积挠度变化最大的截面为(1/8)L处截面；拼装角度变化，累积挠度变化最大的截面为拱脚处截面.

3.2 拱肋合龙状态

结构自重、刚度、温度和拼装角度变化时，拱肋合龙状态下的拱肋各控制截面累积挠度与设计理想状态的比较结果见图4.

图4 四种因素对拱肋合龙状态主拱线形的影响

由图4可知：①随着结构自重的增大，拱脚处截面下挠4%～17%，(1/8)L处截面下挠21%～85%，(1/4)L处截面下挠23%～92%，(3/8)L处截面下挠27%～107%，(1/2)L处截面下挠29%～118%.②随着结构刚度的增大，拱脚处截面上抬3%～10%，(1/8)L处截面下挠6%～22%，(1/4)L处截面下挠7%～24%，(3/8)L处截面下挠7%～26%，(1/2)L处截面下挠8%～27%.③随着结构温度的变化，拱脚处截面累积挠度变化11%～23%，(1/8)L处截面累积挠度变化41%～82%，(1/4)L处截面累积挠度变化54%～108%，(3/8)L处截面累积挠度变化57%～114%，(1/2)L处截面累积挠度变化42%～83%.④随着拼装角度的变化，拱脚处截面累积挠度变化8.22～16.44倍，(1/8)L处截面累积挠度变化4.39～8.78倍，(1/4)L处截面累积挠度变化2.27～4.54倍，(3/8)L处截面累积挠度变化1.67～3.34倍，(1/2)L处截面累积挠度变化1.36～2.55倍.

由上述控制截面挠度变化可得：

1) 拱肋合龙状态下的拱肋线形对不同类型施工误差的敏感性差别很大：对拼装角度最敏感，累积挠度变化最大为16.44倍；对结构自重和温度很敏感，累积挠度变化最大分别为118%和114%；对结构刚度的敏感性较低，累积挠度变化最大为27%.

2) 拱肋合龙状态下的拱肋不同截面累积挠度对同种类型施工误差的敏感性不同.结构自重增大，各控制截面累积挠度变化最大值为17%～118%；结构刚度增大，各控制截面累积挠度变化最大值为10%～27%；结构温度变化，各控制截面累积挠度变化最大值为23%～83%；拼装角度变化，各控制截面累积挠度变化最大值为2.55～16.44倍.

3) 在拱肋合龙状态下，对不同类型施工误差最敏感的截面位置主要为(1/2)L处.结构自重增大，累积挠度变化最大的截面为(1/2)L处截面；结构刚度增大，累积挠度变化最大的截面为(1/2)L处截面；结构温度变化，累积挠度变化最大的截面为(3/8)L处截面；拼装角度变化，累积挠度变化最大的截面为拱脚处截面.

3.3 成桥状态

结构自重、刚度、温度和拼装角度误差变化时，成桥状态下的拱肋各控制截面累积挠度与设计理想状态的比较结果见图5.

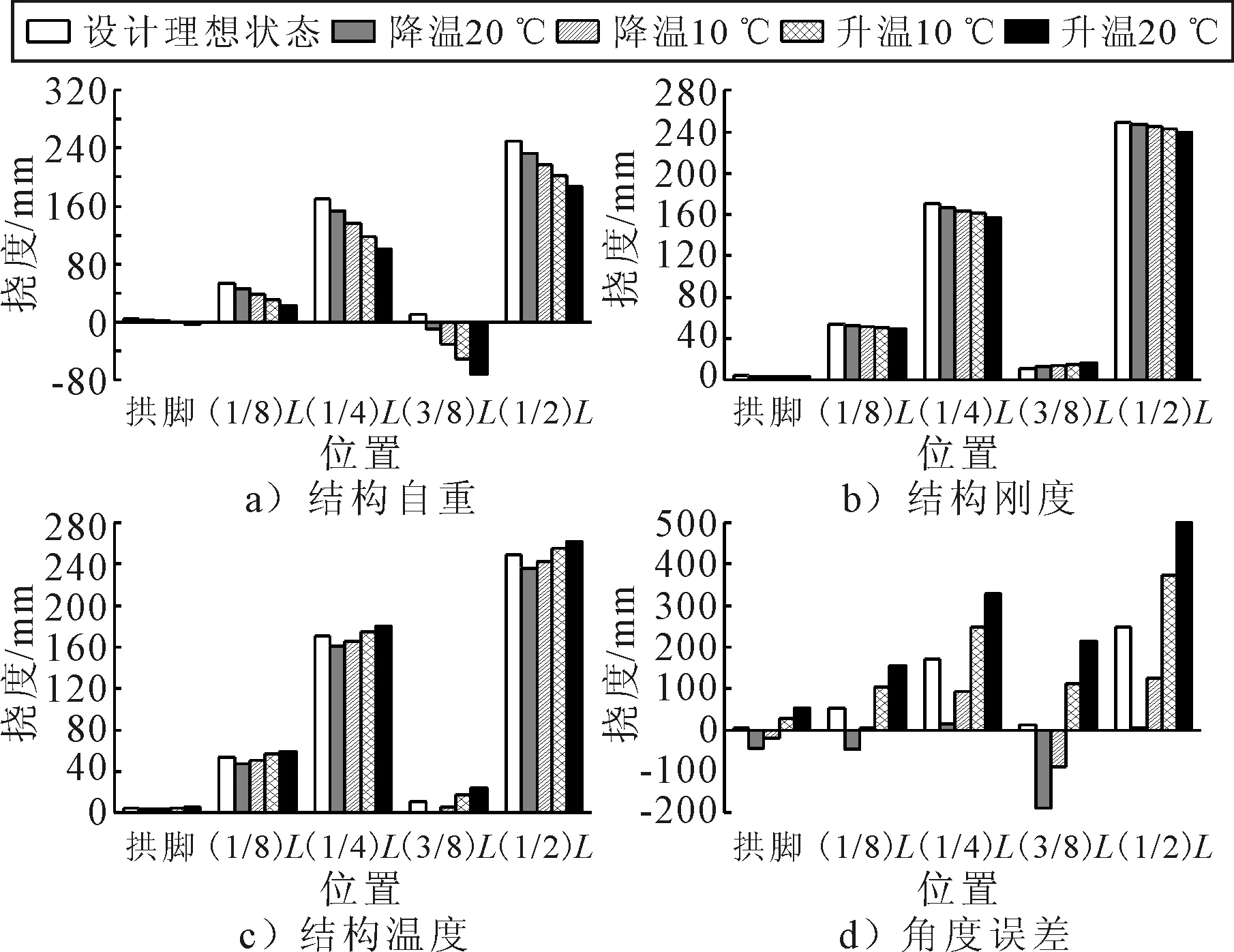
图5 四种因素对成桥状态主拱线形的影响

由图5可知：①随着结构自重的增大，拱脚处截面下挠38%～153%，(1/8)L处截面下挠14%～58%，(1/4)L处截面下10%～40%，(3/8)L处截面下挠1.84～7.37倍，(1/2)L处截面下挠6%～25%.②随着结构刚度的增大，拱脚处截面下挠5%～18%；(1/8)L处截面下挠2%～7%；(1/4)L处截面下挠2%～8%；(3/8)L处截面下挠14%～47%；(1/2)L处截面下挠1%～4%.③随着结构温度的变化，拱脚处截面累积挠度变化10%～19%；1/8L处截面累积挠度变化5%～11%；(1/4)L处截面累积挠度变化3%～6%；(3/8)L处截面累积挠度变化54%～108%；(1/2)L处截面累积挠度变化3%～5%.④随着拼装角度的变化，拱脚处截面累积挠度变化5.57～11.14倍；(1/8)L处截面累积挠度变化0.93～1.88倍；(1/4)L处截面累积挠度变化0.46～0.93倍；(3/8)L处截面累积挠度变化8.88～17.77倍；(1/2)L处截面累积挠度变化0.50～1.00倍.

由上述控制截面挠度变化可得：

1) 成桥状态下的拱肋线形对不同类型施工误差的敏感性差别很大：对拼装角度最敏感，累积挠度变化最大为17.77倍；对结构自重很敏感，累积挠度变化最大为7.37倍；对结构温度较敏感，累积挠度变化最大为108%；对结构刚度的敏感性较低，累积挠度变化最大为47%.

2) 成桥状态的拱肋不同截面累积挠度对同种类型施工误差的敏感性不同.结构自重增大，各控制截面累积挠度变化最大值为25%～7.37倍；结构刚度增大，各控制截面累积挠度变化最大值为4%～47%；结构温度变化，各控制截面累积挠度变化最大值为5%～108%；拼装角度变化，各控制截面累积挠度变化最大值为1倍～17.77倍.

3) 在成桥状态下，施工误差类型不同，累积挠度变化最大的截面位置均为(3/8)L处，最敏感的截面位置相同.

4 结 论

1) 这三种状态下的拱肋不同截面累积挠度均对同种类型施工误差的敏感性不同.建议在施工误差识别中，应根据需识别的误差类型，选择对该种误差最敏感的控制截面进行观测，以便在提高误差识别精度的同时，合理减少测量工作量.

2) 在不同状态下，对施工误差最敏感的主要截面位置不同.最大悬臂状态下最敏感的截面位置主要在(3/8)L处，合龙状态下最敏感的截面位置主要在(1/2)L处，成桥状态下最敏感的截面位置均在(3/8)L处.建议在拱肋悬臂状态下应加强对(3/8)L处截面累积挠度的关注，通过(3/8)L处截面的累积挠度与设计理想状态模型计算结果的对比，对施工误差的大小进行识别.另外，可通过控制(3/8)L处截面的累积挠度满足设计和规范要求的方法对整个拱肋线形进行控制.

3) 这三种状态下的拱肋线形均对拼装角度最敏感，对结构自重和温度比较敏感，对结构刚度敏感性较低.建议将施工误差控制的重点放在拼装角度上，加大力度提高节段拼装角度的精确程度，并在下一节段拼装前，仔细核对已拼前一节段的空间坐标，若拼装角度存在误差及时采取纠偏措施.在最大悬臂状态，应对全天温度和相应温度下的拱肋线形进行跟踪测量，确定拱肋线形与环境温度的对应关系，选择合适的环境温度进行拱肋合龙施工，尽量减小合龙口误差，实现拱肋的无应力合龙.

[1] 孙海涛.大跨度钢桁架拱桥控制问题研究[D].上海:同济大学，2006.

[2] 郭玉龙.大跨度钢桁架拱桥施工控制技术研究[D].成都:西南交通大学，2015.

[3] 张永健.节点刚域效应对斜拉式桁架桥的受力影响[J].长安大学学报(自然科学版)，2007,27(2):42-45.

[4] 魏群.大型钢桁架悬索桥节点刚度对成桥受力影响探讨[J].公路，2009(3):29-33.

[5] 蔡禄荣.大跨度钢桁架拱桥预拱度设置及拼装误差理论研究[D].广州：华南理工大学，2012.

[6] 卢伟升.大跨度钢管混凝土拱桥拱肋施工误差影响分析[J].中外公路，2015,35(3):84-88.

[7] 吴海军.钢-混凝土组合拱桥竖转施工误差分析[J].重庆交通大学学报(自然科学版)，2010,29(1):4-7.

[8] 柳鑫星.拱形钢塔斜拉桥线形控制技术[J].公路，2013(4):36-39.

[9] 王虎胜.基于线形控制的山区大跨度刚构桥合龙方案对比研究[J].公路，2016(7):100-103.

[10] 王海峰.悬臂浇筑预应力混凝土箱梁线形控制技术[J].公路，2010(9):117-119.

Sensitivity Analysis on Construction Error of Long-span Steel Trussed Arch Bridge

KANGJuntao1)HUJie1)DONGPeidong1)XINGYingxing2)CAOHongyou1)SUNXueping1)QINShiqiang1)SHAOGuangqiang1)

(SchoolofCivilEngineeringandArchitecture,WuhanUniversityofTechnology,Wuhan430070,China)1)(ChineseShippingWuhanHarborEngineeringDesign&ResearchInstituteCo.,Wuhan430000,China)2)

The sensitivity of construction error on the linearity of arch ribs for long-span steel trussed arch bridges is analyzed in this paper. Taking the Suling Mountain bridge as an example,the finite element model of the ideal state is used as the benchmark. The influences of self-weight,stiffness,temperature and segment angle errors on arch rib alignment are analyzed under the maximum cantilever state,the closed-loop state and the finished state of arch ribs. The results show that the sensitivity of cumulative deflections of arch ribs with different cross-sections in the three states is different for the same type of construction error. The linearity of arch ribs in these three states is most sensitive to the assembling angle,sensitive to the structure weight and temperature, but low to the structural stiffness. In the different states,the main cross-sectional positions most sensitive to construction errors are different. The paper also puts forward the suggestions of error identification and linear control of arch ribs according to the construction characteristics of this kind of bridge.

steel truss arch bridge; linearity of arch rib; construction error; sensitivity

U448.211

10.3963/j.issn.2095-3844.2017.06.002

2017-09-17

康俊涛(1978—)：男，博士，教授，主要研究领域为桥梁工程

*国家自然科学基金项目(51408449)、湖北省自然科学基金项目(2015CFB393)资助