Bayes理论在雷达探测距离评估中的应用*
2018-01-02王军东
王军东
(中国飞行试验研究院,陕西 西安 710089)
0 引言
机载火控雷达探测距离是机载火控武器系统重要性能指标之一,也是全机系统定型试验中必须验证考核项目,在以往型号试验项目当中,通常雷达探测距离试飞是试验周期长,需要的人力、物力多的试验项目之一。按照国军标要求,为得到置信度较高的试验结果,进入定型试验阶段后,通常试验项目需进行多次重复,从而不可避免地导致了试验周期长、试验成本高等问题,同时也给试验的组织、协调和实施带来了极大难度。也有一些试验总共采集11组数据,将所得数据进行排序,按统计学中P分位数法给出试验结果,该方法虽简单便捷,但是样本量少,导致置信概率偏小[1],可信度不高。
为了解决这些实际问题,需要对现有火控雷达探测距离的试验评估方法进行优化和改进,探索出一种合理的试验方法。要求评估结果可信,同时在定型试验中尽量减少飞行试验架次,小样本 Bayes 方法可以满足试验需求[2]。近年来,国内相关领域的学者和工程技术人员,从理论到工程应用方面,特别在武器装备可靠性、维修性和测试性试验领域,对Bayes小样本理论方面作了大量的研究,并已取得了很好的成果[3-9]。
在火控雷达探测距离的试验中同样适用。通过利用先验信息,使得试验样本总量保持在一定数量。Bayes方法在利用定型阶段试验所获得的样本信息的同时,还充分利用了先验信息。在定型试验之前,通过对试验过程中所获得的先验数据进行分析和决策,使得先验数据的部分或全部参与总体性能的估计[10-13},同样可达到相同的试验目的,使得定型阶段所需的样本数目将大为减少,从而能够有效地缩短试验周期,提高试验效率,降低试验成本。
1 Bayes 验前信息分析
Bayes 方法是目前解决小样本问题的主要方法,在保持检验精度不变的前提下对定型试验阶段试验样本量的要求相比原始方法要小。由于在开展定型试验之前,已经得到了一些验前信息,该验前信息可以弥补定型试验信息的不足。Bayes 小样本统计推断方法就是验前信息的获取和处理。在定型试验中,应用 Bayes 方法来对试验结果进行统计推断,一个重要的环节是必须充分利用验前信息,即在应用当前定型试验信息的同时,还必须考虑其他试验信息的充分利用,包括前期研制试验中的部件试验、分系统试验、系统鉴定试验等信息,只要验前信息的获得接近实际试验条件,则大部分验前信息都可以收集、分析、处理和利用。
火控雷达在进行系统定型试验前,通常要进行设备级、分系统级等大量的研制试飞,最后才进入系统设计定型阶段。按照研制试飞过程特点,雷达探测威力通常是研制阶段首先要摸清的性能,在设备级和分系统级研制试飞阶段已经得到了大量探测距离试验信息。因此,调整试飞阶段的探测距离信息都是宝贵的验前信息,经过分析整理,完全可以应用到定型信息当中。这样雷达探测距离的考核就得到了较多的验前信息量,可以补充到定型试验信息当中,增加定型试验样本。
2 验前信息的应用
根据数理统计原理,雷达探测距离的 Bayes 估计问题就是有定型试验样本(Rfi,1≤i≤n1)和定型之前所得试验样本(Rsi,1≤i≤n2),即调整试验样本,2个样本分别来自正态母体,如何估计定型试验总体分布的分位点。要解决此问题,首先要解决如何估计均值和标准差。首先,如果知道两母体分布无差异。则把调整试验样本合并到定型试验样本中,用合并样本均值和标准差(即完全合并均值和标准差估计) 作估计,这将很好地改进只用定型试验样本信息作出的估计。可实际上,从工程概念上两母体肯定是有联系,但不能确定两母体是否有差异,差异有多大。另外,如果两母体有比较显著的差异,那么无疑用合并均值和标准差作估计,其估计精度会很差。在这种情况下,就需要一种检验方法,就是用一个检验统计量检验两母体是否有显著差异,如果不显著,则用完全合并均值和标准差估计,否则,通过对验前信息调整试验样本进行分析整理,利用调整试验样本提供的信息,避免了只用定型试验样本的样本均值和标准差作估计样本量太少问题,或者对调整试验提供的样本信息全用或不用的错误估计。在实际应用当中,两母体肯定会有差异,比较合理的办法就是根据检验统计量,使用调整试验样本中部分(或全部)数据。
2.1 均值对比法检验验前样本


零假设H0:μs<μf,备择假设H1:μs≥μf
检验步骤如下:
(1)
(2)
(3)
(4)
第2步:计算自由度
ν1=n1-1,ν2=n2-1.
第3步:给出显著性水平α,分别用ν1,ν2查T分布分位数表,得到tα(ν1)和tα(ν2)值,并用式(5)计算:
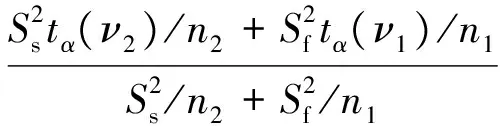
(5)
第4步:计算统计量T的值

(6)
第5步:判断检验结果。
若T>Tα,则拒绝H0,即认为调整试验样本数据可以直接利用;若T≤Tα,则不能拒绝H0,不能直接将调整试验样本数据合并到定型试验样本当中。
2.2 验前样本的剔除-逆序减尾检验法
若以上对比检验结果为T≤Tα,则验前样本不能全部利用,部分验前样本需要剔除。当然,对样本的剔除不能简单地剔除大值或小值。对于定型试验设备而言,试验设备的各项性能,通常会随着试验时间的推移,性能慢慢更趋于稳定,因此,越接近定型阶段所得的验前样本,更能反映设备的工作性能。鉴于此,提出了采用“逆序减尾检验法”,剔除部分验前试验样本,将其余部分验前试验样本合并到定型试验样本当中,来完成总体分布的估计。具体方法如下:
假设开始所得验前试验样本为Rs1,Rs2,…,Rsn2,试验样本排列顺序按所得先后进行排列,即Rs1为验前第1个所得试验样本,Rsn2为验前最后一个所得试验样本。通过以上2.1中的检验步骤,得到检验结果为T≤Tα时,第1次剔除Rs1,用其余n2-1个样本重复进行2.1中的5步检验。若仍不能达到T≤Tα,则继续将Rs1和Rs22个样本剔除,依次重复进行检验,直到T>Tα为止。再将剩余样本用于总体分布的估计。
3 雷达探测距离估计
火控雷达探测距离(记作Rmax),通常是指一定累积概率条件下的检测距离。雷达检测目标也是在特定状态下进行,包括目标的雷达截面积、相对飞行速度和飞行高度,试验载机的飞行高度等。当载机和目标机以一定距离相互接近过程,机组成员在雷达或战术台显示器上最先发现目标的距离,即判定为本次进入雷达对目标的最大发现距离。重复此动作,即可得到雷达探测距离的一组试验样本。
雷达探测距离可定义为试验最大探测距离R的分布函数的p分位点,即
P(R>Rmax)>1-p.
(7)
假设雷达探测距离的分布为正态分布N(μ,σ2),如果记Φ-1(p)为正态分布函数Φ(x)的p分位点。则最大探测距离为
Rmax=μ-Φ-1(p)σ.
(8)
因为R的分布类型已知,μ,σ2未知,现对μ,σ2进行估计,按最大似然法,似然函数为
(9)
将其取对数,并令关于μ,σ2的一阶导数为0,则得

(10)
(11)
(12)
解此关于μ,σ2方程组得μ,σ2的估计值:
(13)
(14)
为了得到σ2的无偏估计用
(15)
从而得到标准差σ的估计:
(16)
通过以上可得,最大探测距离的估计
S.
(17)
在统计学中,样本量在10~30之间,通常认定为小样本,总体为正态分布的处理按小样本进行统计处理,即利用T分布进行统计处理。文中讨论雷达探测距离试验总样本量要求小于30,因此,雷达探测距离试验样本服从非中心T分布,非中心T分布的密度函数为

-∞ (18) 式中:n为自由度;δ=μ/σ为非中心参数,称非心度[14]。 式(7)可转换为 (19) 点tp(n-1)为该T分布的下p分位数。 Φ-1(x)被t1-p(n-1)代换,式(17)可表为 (20) 式(20)中,可通过分位数p值和自由度n-1 值查找T分布分位数表可得。 (21) 通过上述方法,就可得雷达探测距离的 Bayes 估计结果,那么样本总量达到多少组,才使探测距离的估计精度比较合理?由式(13)和(16)可得探测距离平均值的均方根差为 (22) 令 (23) 图1 Q 与观测次数n 的关系曲线Fig.1 Relationship curve between Q and n 雷达最大探测距离是按T分布进行的估计,由于T分布在样本量达到一定程度后,随着样本量的变化,其概率分布曲线形状的变化相当缓慢,也就是T分布分位数值tp(n-1)的变化很小,在样本总量大于20以后,分位数值变化相当缓慢[15],综合考虑,雷达探测距离统计样本总量取20组比较合理。下面以试验数据说明样本总量取20组的合理性。 该试验数据为以往雷达对特定目标的23组探测距离数据,数据按试验先后所得顺序排列。数据结果如下,km: (49.4, 52.8, 46.7, 53.5, 50.8, 39.4, 41.8, 52.6, 43.2, 50.8, 45.2, 44.6, 49.3, 45.5, 48.0, 47.0, 46.5, 48.5, 46.0, 46.5, 49.0, 49.5, 47.5). 对以上样本数据按式(20)估计最大探测距离,按90%探测概率查T分布分位数表,即下p分位数值为0.10。式(20)中,各变量与样本量对应计算结果见表1。从表1最大探测距离估计结果可以看出:随着样本量n的增加,最大探测距离估计结果趋于稳定,在样本量大于20以后,最大探测距离估计值变化很小。 表1 样本量与最大探测距离对应案例Table 1 Case of sample size and maximum detection distance 机载武器装备定型试验中,机载火控雷达指标的验证通常要消耗大量时间,难以满足目前武器急需装备的要求,本文对小样本条件下雷达探测距离的试验评估进行了探索和研究,对研制试验阶段数据通过分析,实现研制阶段试验信息的综合利用,从而完成雷达探测距离指标的考核和鉴定,达到减少试验次数,缩短试验周期,节约试验经费,提高试验效益的目的。 [1] ISO 16269-6-2005,Statistical Interpretation of Data-Determination of Statistical Tolerance Intervals[S].Switzerland:IX-ISO,2005. [2] Thomas Leonard,John S J Hsu. Bayesian Methods:An Analysis for Statisticians and Interdisciplinary Researchers[M].Cambrige:Cambridge University Press,1999. [3] 张学东.基于贝叶斯方法的导弹维修性试验与评定研究[J].现代防御技术,2013,41(1):31-36. ZHANG Xue-dong.Research on Missile Maintainability Test and Evaluation Based on Bayesian Method[J].Modern Defence Technology,2013,41(1):31-36. [4] 王敏,杨江平,卢雷,等.利用分系统数据制定整机测试性验证试验方案[J].现代防御技术,2015,43(5):213-217. WANG Min,YANG Jiang-ping,LU Lei,et al.Making the Test Verification Scheme of The Whole System by Using the Data of Subsystem[J].Modern Defence Technology,2015,43(5):213-217. [5] 汤巍,景博,黄以锋.小子样变总体下的Bayes测试性验证方法[J].系统工程与电子技术,2014,36(12):2566-2570. TANG Wei,JING Bo,HUANG Yi-feng.Testability Verification Method Based on Bayes Theory Under Small Sample and Varying Population Circumstance[J].Systems Engineering and Electronics,2014,36(12):2566-2570. [6] 贾旭山,金振中.Bayes 假设检验及样本数量问题研究[J].现代防御技术,2012,20(4):67-70. JIA Xu-shan,JIN Zhen-zhong.Bayes Hypothesis Testing and Sample Quantity[J].Modern Defence Technology,2012,20(4):67-70. [7] 王睿,牛海,徐亚光.基于评估需求的舰艇通信训练数据挖掘研究[J].现代防御技术,2016,44(6):54-60. WANG Rui,NIU Hai,XU Ya-guang.Research on Data Mining of Warship Communication Training Based on Evaluation Requirement[J].Modern Defence Technology,2016,44(6):54-60. [8] 刘琦,武小悦.Bayes方法应用中验前分布选择的一致性与可信性原则[J].系统工程与电子技术,2010,32(11):2356-2359. LIU Qi,WU Xiao-yue.Principles of Consistency and Reliability for Prior Distributions Selection in Bayesian Method Application[J].Systems Engineering and Electronics,2010,32(11):2356-2359. [9] 韩旭,王建宇,祖先锋.基于Bayes序贯检验的长周期系统动态试验方法[J].系统工程与电子技术,2012,34(9):1957-1965. HAN Xu,WANG Jian-yu,ZU Xian-feng.Dynamic Test Methodology for Long-Working Systems Based on Bayesian Sequential Test Theory[J].Systems Engineering and Electronics,2012,34(9):1957-1965. [10] 徐廷学,刘勇,赵建忠,等.维修性先验信息的融合方法[J].系统工程与电子技术,2014,36(9):1887-1892. XU Yan-xue,LIU Yong,ZHAO Jian-zhong,et al.Fusion Method of Prior Maintainability Information[J].Systems Engineering and Electronics,2014,36(9):1887-1892. [11] 应新雅,张志华.产品可靠性新型顺序约束及评估算法改进[J].系统工程与电子技术,2015,37(2):468-472. YING Xin-ya,ZHANG Zhi-hua.Improvement on the New Ordering Constraints Evaluation Algorithm of Product Reliability[J].Systems Engineering and Electronics,2015,37(2):468-472. [12] 雷华军,秦开宇.确定测试性验证试验方案的贝叶斯方法[J].系统工程与电子技术,2012,34(12):2612-2616. LEI Hua-jun,QIN Kai-yu.Bayesian Method for Determination of Testability Demonstration Test Scheme[J].Systems Engineering and Electronics,2012,34(12):2612-2616. [13] 夏佩伦,李本昌,李博.假设检验在军事工程应用中的若干问题[J].火力与指挥控制,2015,40(3):100-103. XIA Pei-lun,LI Ben-chang,LI Bo.Some Issues Concerning Applications of Hypothesis Testing in Military Engineering[J].Fire Control & Command Control,2015,40(3):100-103. [14] 闫章更,魏振军.试验数据的统计分析[M].北京:国防工业出版社,2001:27-30. YAN Zhang-geng,WEI Zhen-jun.Statistical Analysis of Test Data[M].Beijing:National Defense Industry Press,2001:27-30. [15] Robert E McShea.Test and Evaluation Aircraft Avionics and Weapon Systems[M].Mojave CA:SciTech.2005:601-602.

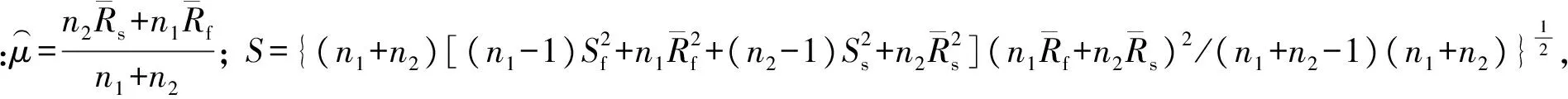

4 试验验证




5 结束语
